基于擴展有限元研究非均質材料的應力強度因子

蘇毅, 王生楠, 劉儉輝

(西北工業大學 航空學院, 陜西 西安 710072)

為了更好地了解非均質材料的力學性能,常用有限元法對這種材料進行仿真分析。但是,常規有限元法網格依賴性使之在處理連續-非連續問題時表現出明顯的局限性。擴展有限元(XFEM)在處理這類不連續問題表現了極大的優勢。因為XFEM[1-3]所使用的網格與結構內部幾何或物理界面無關,從而克服了裂紋尖端等高應力和變形集中區內網格劃分的困難,使得在模擬裂紋生長過程中無需對網格進行重新劃分。網格劃分也無需與材料細觀結構的內部邊界相協調。XFEM在處理不連續問題上的優點使其從問世以來,在國際上得到了很快的發展和廣泛的應用。Zhang H.H.等人[4]用XFEM模擬了粘彈性材料的夾雜問題。2006年,文獻[5]用擴展有限元對正交各向異性材料中的裂紋采用了新的加強法。用算例證明了他的準確性。王志勇等[6]運用不含裂尖增強函數的擴展有限元法,分別研究了靜態及動態載荷作用下顆粒增強復合材料的斷裂行為。假定基體和顆粒都為線彈性材料并且綁定完好,研究了不同顆粒位置、數量對基體裂紋尖端斷裂參數的影響。數值模擬結果清晰地顯示了含剛性顆粒和柔性顆粒時不同的失效機制。

本文的主要內容:①建立了含夾雜的帶裂紋問題的位移場給出了均勻材料的相互作用積分和非均質材料的相互作用積分;②介紹了本文的相互作用積分的離散問題；③用3個算例模擬了帶顆粒夾雜加強的裂紋板,軟硬顆粒對應力強度因子或能量釋放率的影響。

1 XFEM的基本原理

1.1 單位分解法

1996年Melenk和Babuska[7]及Duarte和Oden[8]先后提出了單位分解法(PUM),其基本思想是任意函數φ(x)都可以用域內一組局部函數Ni(x)φ(x)表示,即

(1)

式中：Ni(x)為有限元形函數,它形成一個單位分解

(2)

基于此,可以對有限元形狀函數根據需要進行改進。XFEM是基于PUM對單元的形函數加以改進,從而考慮所研究問題的不連續、奇異性和邊界層等特性。

1.2 位移逼近方程的建立

符合單位分解概念的向量函數u的逼近具有下列形式:

(3)

式中:Ni為有限元形函數,φα為改進函數,M表示改

進函數個數,根據(3)式,有限元空間(φ1≡1,其他φα≡0)將是改進空間的子空間。

XFEM的重點就集中在用最少的加強函數來描述不連續問題如裂紋位移逼近函數。用不連續函數和二維漸進裂紋尖端位移場來建立各向同性線彈性的裂紋模型。用水平集函數來建立材料界面的局部改進函數,這使得在裂紋擴展時不需要重新劃分網格。

圖1 裂紋和顆粒需要改進的自由度的節點集

擴展有限元的位移逼近為:

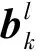
當節點為常規單元的節點時,只有第1項;當節點為被裂紋貫穿單元的節點時,有第1項和第2項;當節點為裂紋尖端所在單元的節點時,有第1項和第3項;節點同時處于裂紋貫穿單元和裂紋尖端所在單元,應優先屬于裂紋尖端所在單元,加強方式選擇裂紋尖端所在單元節點加強方式。當節點屬于夾雜單元節點時,有第1項和第4項。也就是說當板中只有裂紋的話只需要前3項,當板中只有夾雜的話需要第1項和第4項,當板中同時有裂紋和雜質時,4項都需要。

1.3 XFEM離散方程的建立

和常規有限元方法一樣,將(4)式代入彈性體的虛功方程,可導出XFEM的支配方程為

Kδ=F

(5)

式中：δ是節點位移列陣,K和F分別為結構總剛度矩陣和節點載荷列陣,K按常規步驟由單元剛度矩陣組集而成。單元層次上的k和f分別為

(6)

單元荷載列陣f:

(7)

子矩陣和單元荷載力矢量分量表示如下:

(8)

(9)

(10)

(11)

(12)

常規應變矩陣:

(13)

裂紋貫穿單元附加應變矩陣:

(14)

裂紋尖端單元附加應變矩陣:

(15)

夾雜單元附加的應變矩陣:

(16)

1.4 裂紋尖端應力強度因子計算

傳統的J-積分形式為:

(17)

式中:Γ是積分路徑,nj是該路徑上弧元素外法線的方向余弦。加入輔助場后得到J-積分形式為:

(18)

選取輔助場形式為:

(19)

(20)

將(18)式展開,交叉部分為相互作用積分可以表示為:

(21)

式中：q為權函數,mi為單位法向量。當裂尖的積分區域包含夾雜顆粒區域,也同時包含了2種材料的界面。因此積分區域是非均質材料的積分。此時如果材料在空間上具有光滑變化的屬性時,同時將線積分轉化為面積積分。相互作用積分可表示為:

(22)

Ih為均勻材料的相互積分,Inonh為材料非均勻性衍生出的項。

εij=Sijkl(x)σkl(i,j,k,l=1,2)

(23)

從上面的定義發現,輔助應力場(20)式由于不涉及材料屬性,是平衡的。但除了裂尖點之外,輔助位移場和輔助應變場之間的關系部再成立。定義裂尖處的應變場。

(i,j,k,l=1,2)

(24)

(25)

Ih為均勻材料的相互積分,Inonh也可以表示為:

(26)

考慮不計體力的平衡狀態及應力張量的對稱性,有

此時上式可簡化為:

εjkδ1j),iqdA

(27)

因為

(28)

經過變換包含材料界面的相互作用積分表達式為:

(29)

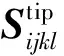
(30)

至此,可以看出當裂紋尖端距離顆粒很近時,(29)式的積分仍是可行的。但如果裂尖距離顆粒非常近或已經落在材料界面上時,應力不再滿足反平方根奇異性,則需選取相對應的輔助場計算。當積分區域包含材料界面,如圖2所示。

圖2 裂尖局部坐標系及相互作用積分區域

對于各向同性材料相互作用積分與應力強度因子的關系可以表示為:

(31)

式中：

(32)

1.5 裂紋擴展方向

判斷裂紋擴展方向常用的準則有:最大周向拉應力準則、最大周向拉應變準則、最小應變能密度強度準則、等應變能密度線上最大周向拉應力準則、能量釋放率準則等[10],其中以最大周向拉應力準則計算最為簡便。在最大周向拉應力準則里,裂紋尖端擴展方向θc由下式確定:(非均質有顆粒)

(33)

為了模擬裂紋的擴展過程,可采用裂紋增量形式。

2 相互作用積分的數值離散

在XFEM中為了很好地運用相互作用積分,(29)式可以被離散為:

(34)

式中：eA是積分區域A的的單元的數量;pe在單元中積分點的數量;|J|p為雅克比行列式;wp為積分點p的權重。實際位移的導數為:

(35)

對于非均質材料,建立剛度矩陣時,材料屬性按照積分點的材料屬性選取。由于在形函數的變分矩陣中含有不連續的函數,對裂紋分割單元,夾雜單元如果直接進行高斯積分,計算的結果是不準確的。文獻[11-13]給出了積分策略。在本文中,對于常規單元采用2階Gauss積分,對于混合單元采用6階Gauss積分,對于裂紋貫穿和夾雜的單元,進一步細分成子三角形單元,每個子三角形單元采用3階Gauss積分,對于裂尖單元,進一步細分成子三角形單元,每個子三角形單元采用7階Gauss積分。

3 數值算例

算例1 無限大板中心裂紋與單個圓形顆粒間的相互作用

圖3 帶圓形夾雜顆粒的中心裂紋板

表1 Wang和Chau[14](E2/E=∞,υ=0.35)

表2 本文結果(E2/E1=104,υ=0.35)

通過比較發現,本文結果和Wang和Chau[14]的結果相對誤差很小,證明了合理性。當b/a增大時,KI(-a)/K0和KI(a)/K0隨之增大,說明當裂紋與顆粒的位置越遠時,顆粒加強的作用會減小。

算例2 單邊裂紋擴展與單個圓形顆粒間的相互作用

如圖4所示,一個二維平板尺寸為H×L,受到單向拉伸載荷σ作用,其內部含一個長度為a的邊裂紋,圓形顆粒半徑為R。顆粒中心與裂紋尖端垂直距離為b,H=15;L=15;b/R=1;a/L=1/15;R=a;EP/E=100,10,5或是EP/E=0.01,0.1,0.2下標P代表板的彈性模量υ1=υ2=0.35;σ=1;KI0為沒有顆粒夾雜時裂紋尖端的應力強度因子,裂紋擴展60次,每次步長為0.2。

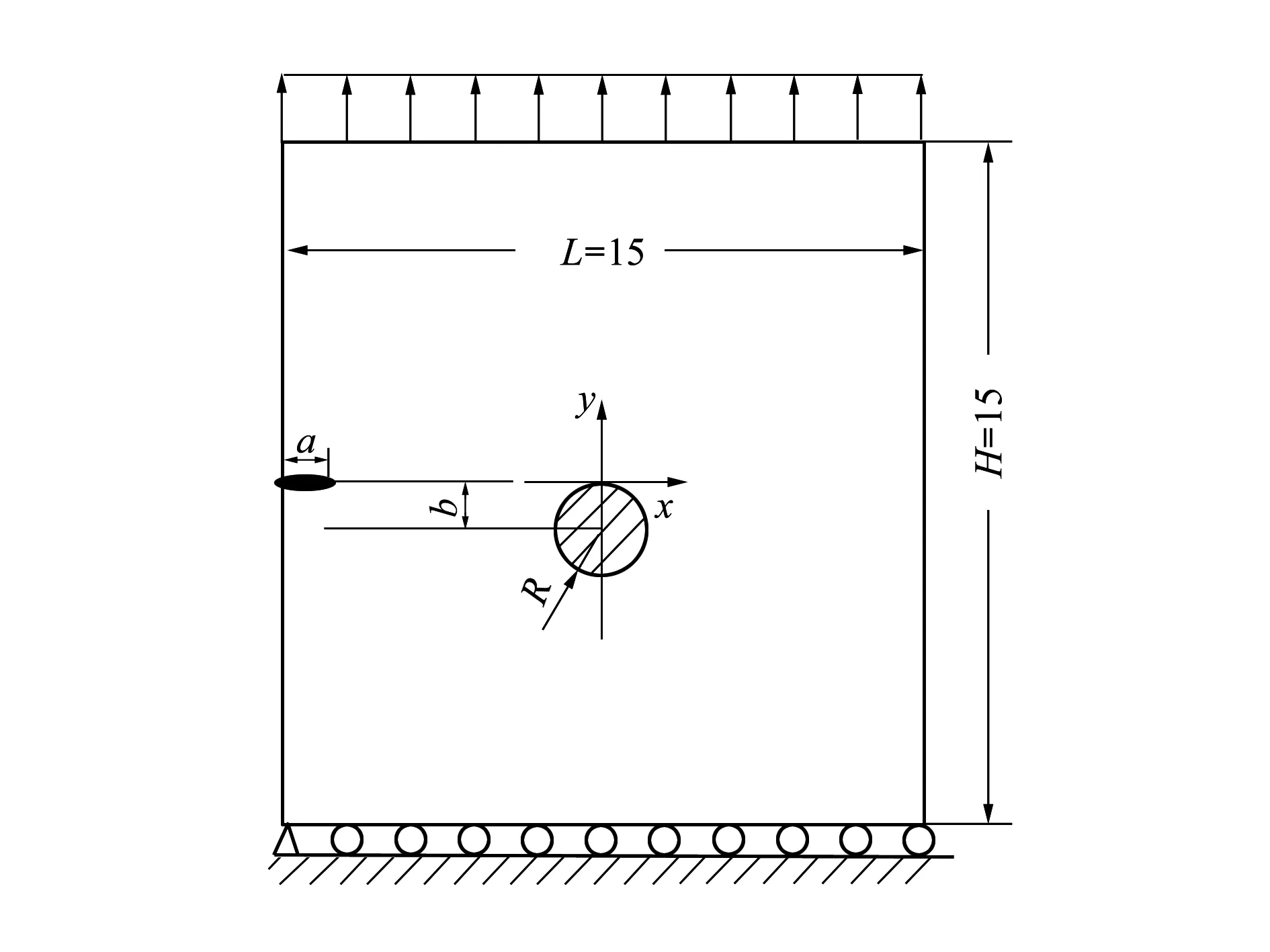
圖4 帶圓形夾雜顆粒的單邊裂紋板

圖5表示在軟硬顆粒下,裂紋擴展軌跡。在軟顆粒的時候,裂紋擴展偏向顆粒,顆粒彈性模量越小最后裂紋越靠近顆粒。這證明了裂紋的擴展偏向于強度小的地方,在無顆粒的情況下,裂紋的路徑基本沒有什么改變,在勻質板的情況下,裂紋路徑沒什么改變。同樣硬顆粒的時候,裂紋擴展遠離顆粒。顆粒的彈性模量越大最終越偏離原來軌跡。

圖6表示無量綱量KI/KI0隨著x/R變化趨勢, 對于硬顆粒而言,應力強度因子一直比無顆粒的時候小,說明了硬顆粒的確對板有加強作用,顆粒的彈性模量越大對板的加強效果越明顯。而對軟顆粒而言,應力強度因子比無顆粒加強時大,軟顆粒降低了板的強度,從圖中可以看出在x/R在-2到0的區間,顆粒對板的加強或減弱作用明顯。

圖5 裂紋擴展軌跡圖6 裂紋擴展時,KI/KI0的變化

算例3 孔邊單裂紋擴展與單個圓形顆粒間的相互作用

如圖7所示,一個二維平板尺寸為L×H,受到單向拉伸載荷σ作用,其中心有一個孔洞半徑為R孔邊有一長度為a的裂紋,圓形顆粒半徑為R。其離孔洞中心的水平距離為b=4.5,H=15;L=15;a/W=1/30;R=a;Ep/E=100,10或是Ep/E=0.01,0.1;下標p代表顆粒的彈性模量;υ1=υ2=0.35;σ=1;G0為沒有顆粒夾雜時裂紋尖端的能量釋放率,裂紋擴展16次,每次步長為0.2.c=0.2,0.5。

圖8表示無量綱量G/G0隨著x變化趨勢,對于硬顆粒而言,能量釋放率一直比無顆粒的時候小,說明了硬顆粒的確對板有加強作用,顆粒的彈性模量越大對板的加強效果越明顯。G/G0隨著x增大越來越小,也就是隨著裂紋尖端越靠近硬顆粒,硬顆粒對裂紋尖端的能量釋放率的影響越明顯。距離c對G/G0影響也很明顯,c越小影響越明顯。而對軟顆粒而言,能量釋放率比無顆粒加強時大,軟顆粒降低了板的強度,隨著裂紋尖端越靠近軟顆粒,硬顆粒對裂紋尖端能量釋放率的影響越明顯。 因為裂紋板是不對稱的,裂紋的擴展路徑是偏離水平方向的。

圖7 帶圓形夾雜顆粒的孔邊單裂紋板 圖8 裂紋擴展時,G/G0的變化 圖9裂紋擴展的軌跡(放大)

4 結 論

1) 應力強度因子是基于2個相容許的場實際場和輔助場。

2) 用擴展有限元計算裂紋擴展時很方便,不用在裂紋尖端重新劃分網格。

3) 顆粒對材料的強度的增加或減弱有很明顯的作用。

參考文獻：

[1] Daux C, Mo?s N, Dolbo W J, Sukumar N, Belytschko T. Arbitrary Branched and Intersecting Cracks with the Entended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2000, 48: 1741-1760

[2] Mo?s N, Dolbow J, Belytschko T. A Finite Element Method for Crack Growth without Remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46:131-150

[3] Sukumar N, Srolovitz D J, Baker T J, Prevost J H. Brittle Fracture in Polycrystalline Microstructures with the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 1999, 45: 601-620

[4] Zhang H H, Li L X. Modeling Inclusion Problems in Viscoelastic Materials with the Extended Finite Element Method[J]. Finite Elements in Analysis and Design, 2009, 45: 721-729

[5] Asadpoure A, Mohammadi S. Developing New Enrichment Functions for Crack Simulation in Orthotropic Media by the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2007, 69:2150-2172

[6] 王志勇,馬力,吳林志,于紅軍. 基于擴展有限元法的顆粒增強復合材料靜態及動態斷裂行為研究[J]. 固體力學學報,2011,32(6): 566-573

Wang Zhiyong, Ma Li, Wu Linzhi, Yu Hongjun. Investigation of Static and Dynamic Fracture Behavior of Particle-Reinforced Composite Materials by the Extended Finite Element Method[J]. Chinese Journal of Solid Mechanics, 2011, 32(6):566-573 (in Chinese)

[7] Melenk J M, Bubska I. The Partition of the Unity Finite Element Method: Basic Theory and Applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 289-314

[8] Duarte G A, Oden J T. An H-P Adaptive Method Using Clouds[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 237-262

[9] Yu H J, Wu L Z, Guo L C, Du S Y, He Q L. Investigation of Mixed-Mode Stress Intensity Factors for Nonhomogeneous Materials Using an Interaction Integral Method[J]. International Journal of Solids and Structures, 2009, 46:3710-3724

[10] 張行. 斷裂力學[M]. 北京:中國宇航出版社, 1990

Zhang Hang. Fracture Mechanics[M]. Beijing: China Aerospace Press, 1990 (in Chinese)

[11] Laborde P, Pommier J, Renard Y, Salaun M. High-Order Extended Finite Element Method for Cracked Domains[J]. International Journal for Numerical Methods in Engineering, 2005, 64: 354-381

[12] Mousavi S E, Xiao H, Sukumar N. Generalized Gaussian Quadrature Rules on Arbitrary Polygons[J]. International Journal for Numerical Methods in Engineering, 2010, 82: 99-113

[13] Natarajan S, Bordas S, Mahapatra D R. Numerical Integration over Arbitrary Polygonal Domains Based on Schwarz-Christoffel Conformal Mapping[J]. International Journal for Numerical Methods in Engineering, 2009, 80:103-134

[14] Wang Y B, Chau K T. A New Boundary Element Method for Mixed Boundary Value Problems Involving Cracks and Holes: Interactions between Rigid Inclusions and Cracks[J]. International Journal of Fracture, 2001, 110: 387-406