基于側滑配平的單副翼極限位置卡死控制方法研究

吳成富, 邵朋院, 戢鳳

(西北工業大學 無人機特種技術重點實驗室, 陜西 西安 710065)

舵面卡死是無人機一種常見故障,該故障會對無人機飛行的安全性和操縱性產生不利影響。文獻[1]指出,在單側副翼卡死情況下,飛機很容易進入荷蘭滾模態,嚴重影響飛機的飛行安全。該文獻還從力矩平衡的角度得出了單側副翼卡死在什么范圍內時,可以利用其他操縱面來進行補償。該文獻的分析結果對單副翼有限卡死情況下進行容錯控制的可能性提供了理論依據。

針對舵面故障的控制,國內外很多研究者進行了相關研究,取得了不少研究成果，例如文獻[2-4]。可以看出,上述文獻中的研究集中于舵面卡死在有限位置的情況,其中給出的單側舵面卡死的最大幅值分別為11.46°[2]、2.29°[3]和1.43°[4],這距離一般飛機操縱面的極限位置還有很大幅度(一般飛機的操縱面極限位置均在20°～30°),同時注意到,上述文獻采用的補償方法均為使用剩余操縱面來對卡死舵面進行補償。所以,使用上述文獻中的方法,無法處理操縱面極限位置卡死的故障。

而操縱面極限位置卡死在飛機舵面故障中時有發生,但對于該問題,在作者查閱到的文獻范圍內,還沒有研究者給出解決方法,不過科林斯公司的D B.Jourdan等人在容損控制方案[5]中提出的全姿態控制器(all attitude autopilot)可以為該問題的解決提供一定思路。全姿態控制器(后文中縮寫為AAA)設計初衷是用于飛機在進行大姿態機動的一種控制方法,該方法的核心思想是將整個飛機作為一個操縱面,利用氣流角(迎角和側滑角)產生額外的操縱力矩,彌補在某些極端情況下舵面操縱能力不夠的限制,文獻[5]利用AAA實現了在單側機翼翼面矩損傷80%的情況下繼續穩定飛行,并進行了試飛驗證,證明了AAA在飛機舵面操縱能力不足情況下巨大的應用價值。

本文提出了一種基于AAA思想的容錯控制方案,當飛機單側副翼極限位置卡死時,使飛機產生側滑角,來提供額外的滾轉力矩,以補償副翼卡死帶來的不對稱力矩。仿真結果表明,該方法可以使飛機的滾轉姿態快速穩定下來,并逐漸恢復未卡死副翼的操縱能力,從而避免由于副翼極端位置卡死而造成的事故。

1 單側副翼卡死飛機的配平分析

從文獻[1]的分析結果可以看出單側副翼卡死對于橫側向力矩(滾轉力矩和偏航力矩)影響較大。其中,對于滾轉力矩的影響最大,而且單側副翼卡死

使得滾轉力矩的配平能力大幅降低,所以配平的關鍵是如何配平滾轉力矩。

從前文可知,要實現單側副翼極限位置卡死的配平,只使用剩余舵面的操縱能力是遠遠不夠的。所以,需要充分挖掘飛機的滾轉操縱能力,可以從飛機的滾轉力矩系數組成來進行分析。

飛機的滾轉力矩系數表達式如下:

cl=clββ+clδαrδαr0+clδrδr+clδalδαl+clpp

(1)

式中：cl為滾轉力矩系數;β為側滑角;δαl為左副翼;δαr0為右副翼卡死位置;cl*為滾轉力矩對各個量的氣動導數。

從(1)式可以看出,除了舵面可以產生滾轉力矩外,側滑角也可以產生滾轉力矩,所以,可以使用側滑角對單側副翼卡死后的飛機進行滾轉力矩配平。下面分析引入側滑角配平的優缺點。

從(1)式可知,當加入側滑角時,能夠減小其他舵面的配平量,特別是減小左副翼的配平量,能夠增加飛機剩余的操縱能力。

圖1為以某小型無人機為例,對于右副翼在極限位置(20°)的情況進行水平直飛配平,

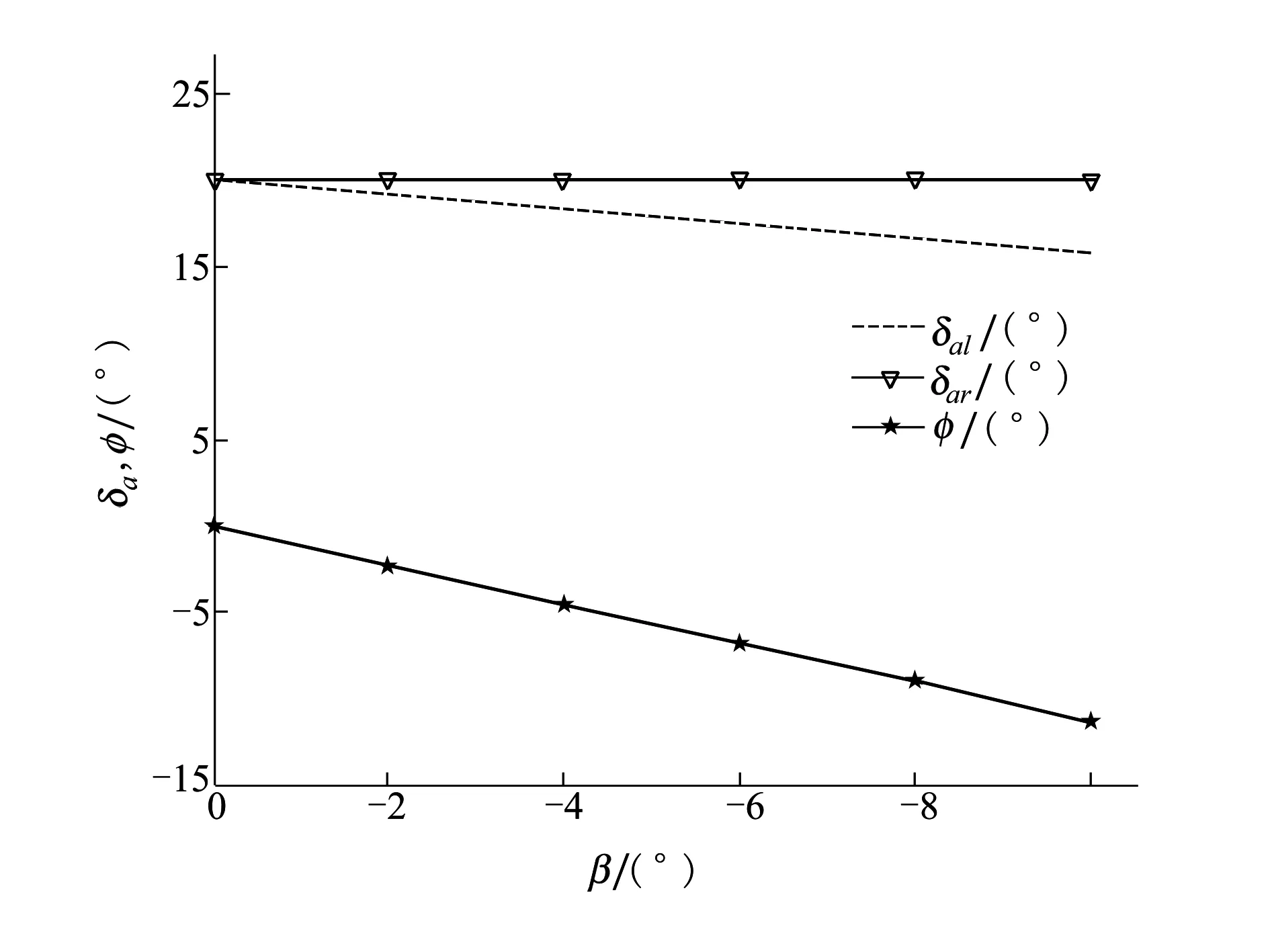
圖1 右副翼極限位置卡死配平曲線

從圖1可以看出,若不加入側滑角,則左副翼也得偏轉到極限位置(20°),才能實現水平直飛,隨著側滑角的加入,左副翼偏度逐漸減小,加入-10°側滑時,左副翼偏度減小了4.12°,但同時滾轉角增加了11.15°。

從上面理論分析和實際配平的結果可以看出,在配平中增加側滑角和左副翼各有利弊:

·增加側滑角可以使飛機具有較大的剩余操縱能力,但會增加飛機的滾轉角,同時會增大阻力。

·增加左副翼可以減小飛機的側滑和滾轉,但是會減小剩余操縱能力。

2 舵面卡死控制器設計

2.1 控制器結構

控制器的主要目的是產生合理的側滑角指令并對其進行控制。

飛行控制律設計仍然采用縱向和橫側向模態分開設計的方法,其中,縱向采用高度保持控制律,使飛機可以實現定高飛行,橫側向采用側滑角保持控制律。其中,高度保持控制律與正常飛機的類似,采用俯仰角保持作為內回路,設計方法和結果在此不再贅述。

橫側向控制器由兩部分組成,一部分為側滑角指令生成器,用于監控飛機舵面狀態,生成側滑角指令;另一部分為側滑角控制器,用于實現指令生成器生成的側滑角指令。

整個控制器結構如圖2所示。

圖2 控制器結構總框圖

圖2中背景有斜線的模塊即為橫側向控制器,為本文中重點研究的內容。

2.2 側滑角控制器設計

側滑角導數如下式所述:

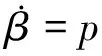
(2)

從(2)式可知,偏航角速率、滾轉角速率以及側向力都對側滑角的建立有貢獻,而前2個角速率需要使用副翼和方向舵來產生,而側滑角建立起之后,會產生側力,需要建立滾轉角,通過升力分量來平衡該側滑角。所以,側滑角采用副翼和方向舵協調控制的方法,使用滾轉角和偏航角控制作為內回路。

控制器結構如圖3所示。

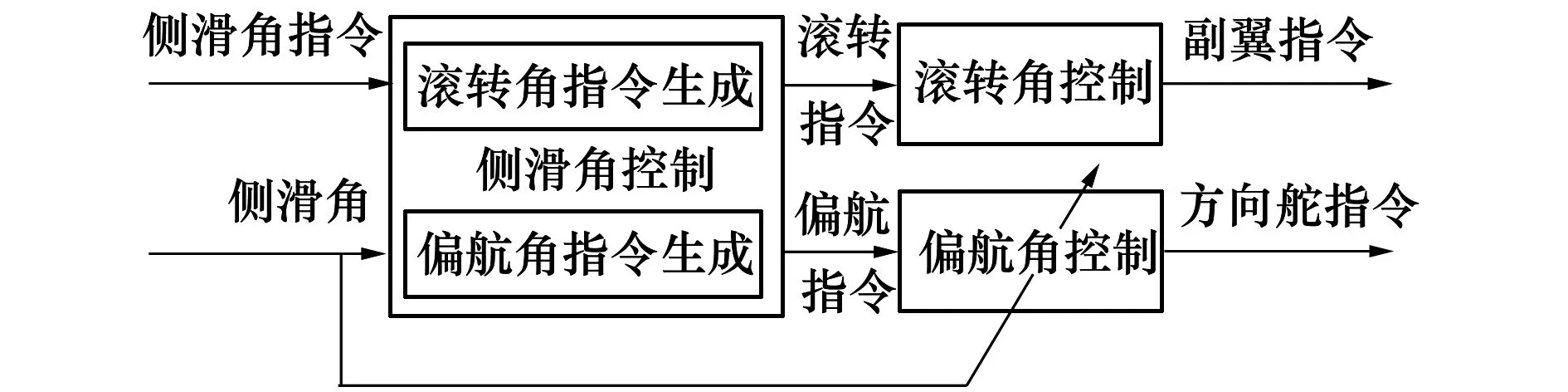
圖3 側滑角保持控制器框圖

側滑角保持控制器由內環姿態控制和外環的姿態指令生成(即圖3中的側滑角控制)組成,其中外環由側滑角偏差來生成滾轉和偏航指令,內環分別使用副翼和方向舵來實現姿態角的控制,需要注意的是其中偏航角控制與常規的偏航角控制不同,其主要目的并不是控制偏航角,而是使用方向舵來配合產生側滑角,并使側滑角到達穩態時航向達到穩態,實現穩態側滑直飛。圖3中各個控制器都采用經典的PID控制律,其中在參數設計過程中,發現偏航角控制的參數隨側滑角變化較大,所以,偏航角采用增益調度PID控制。

其中,側滑角控制器根據側滑角誤差來生成滾轉指令和偏航指令,使用PI控制,控制律如下:

(3)

滾轉角保持使用PD控制,控制律如下所示：

δa=Kpa*(φc-φ)-Kda*p

(4)

偏航角保持使用PD控制,控制律如下所示:

δr=Kpr*(ψc-ψ)-Kdr*r

(5)

從圖1可知,在右副翼極限卡死時,要給左副翼留出一定的操縱余量,需要加入較大的側滑角(要留4°操縱余量時側滑角打到10°),而在側滑角變化過程中,飛機橫航向氣動特性變化較大,控制律設計時分別選取側滑角為0、-3、-6、-9°穩定側滑直飛狀態4個設計點,使用傳統頻域校正方法調整參數,在調參的同時觀察其時域響應,使其滿足給定的時域及頻域指標,由于篇幅限制,設計結果省略。

作者在調參時發現,側滑角為-9°時縱向及滾轉角控制的參數均可以滿足其他設計點的設計要求,而偏航通道的參數不能滿足其他設計點的設計要求,需要根據側滑角的值進行增益調度。

其中,增益調度采取指數過渡規則,在2個設計點之間的過渡規則如下:

(6)

式中：K0和Kf分別為距離當前工作點最近的2個設計點參數,τ∈[0,1]為指數過渡的比例系數,表示當前工作點在相鄰2個設計點之間的歸一化距離,計算公式如下:

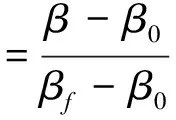
(7)

式中：β0和βf分別為與K0和Kf對應的相鄰2個設計點的側滑角值。

2.3 自適應指令生成器設計

自適應指令生成器通過監控副翼位置來判斷是否有副翼卡死,并在一片副翼卡死時,根據另一片副翼的狀態給出適當的側滑角指令,使得一片副翼卡死后,飛機橫側向運動能夠快速穩定下來,并在快速穩定之后加入側滑角使得另一片副翼能保留足夠的操縱余量。為了簡單可靠,該策略依然沿用成熟的PID控制形式。

設檢測到右副翼卡死,則側滑角指令生成策略如下所述:

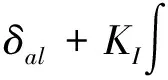
(8)

式中：

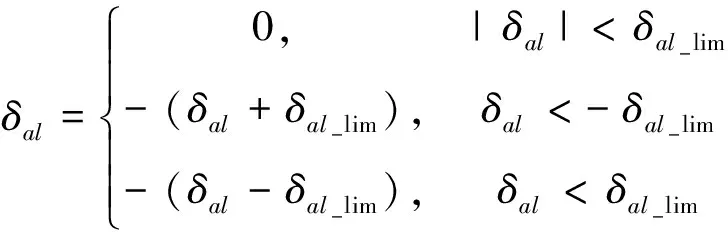
(9)

式中:δal-lim為限定的性能恢復后左副翼的最大偏度,本文中結合所研究飛機的氣動數據,取δal-lim=16°,即在性能恢復結束后,左副翼偏度不能大于16°,即左副翼必須留足不小于4°的操縱余量。

上述策略在處理舵面卡死時會有2個階段:

·在右副翼剛卡死時,滾轉角大幅增加,側滑角指令為0°,為了保持該0°側滑角,左副翼偏度迅速增大(在該模型中達到了極限位置20°),將飛機的滾轉姿態穩定下來。該階段為快速穩定階段,在該階段左副翼補償起主要作用,但該階段結束時,左副翼的剩余操縱能力幾乎為0,所以需要第二階段恢復左副翼的操縱能力。同時注意到,該階段持續時間很短,所以對飛機飛行安全性影響不大。

·在左副翼超過16°之后,在(8)式的作用下,開始加入側滑角,直至左副翼偏角回到16°以內,飛機最終進入一個穩定側滑飛行狀態。該階段為操縱能力恢復階段,主要作用是利用側滑角使左副翼偏角減小,恢復副翼的滾轉操縱能力。

從上述分析可以看出,使用上面的策略生成側滑角,可以根據副翼的狀態自動調整側滑角指令,既能使飛機從單側副翼卡死的情況下快速穩定下來,又能在穩定之后逐漸恢復飛機的操縱能力,所以上述策略是合理的。

通過在非線性模型中調整,發現KP和KI2個系數對指令生成和系統響應會產生如下影響:

·KP增大會提高指令生成和系統響應的快速性,但會使系統響應超調增加,同時會使穩態時的側滑角指令降低,未卡死舵面的穩態值增加。

·KI增大會使穩態時的側滑角指令增大,未卡死舵面的穩態值減小,但過大的KI會使系統震蕩甚至失穩。

根據上述分析,響應的快速性和剩余操縱余量是一對矛盾,本文在保證穩態時線性系統穩定裕度的前提下,對快速性和剩余操縱余量采取加權最優準則,將指令生成器的參數調節問題歸結為一個最優化問題,如下式所述:

(10)

(11)

注:(11)式中下標f表示尋優過程的響應終值。

使用非線性模型,在Matlab中的使用fminsearch函數,在空中飛行階段,取λ1=0.4,λ2=0.6,求解最優化問題,得到一組最優解:

取該組解時穩定裕度為:

GM=10.096 696 dB

PM=80.006 087°

使用自適應指令生成器結合上述側滑角保持控制律,非線性仿真結果見下節。

3 仿真結果及其分析

為了驗證文中設計的自適應指令生成器和側滑角保持控制器在非線性模型中的響應,進行非線性仿真。仿真初始階段,飛機在500 m高度,以25 m/s空速保持水平直飛,在仿真5 s時,右副翼卡死在極限位置(20°),整個過程中自適應指令生成器都在工作。整個過程中各個量響應如下:

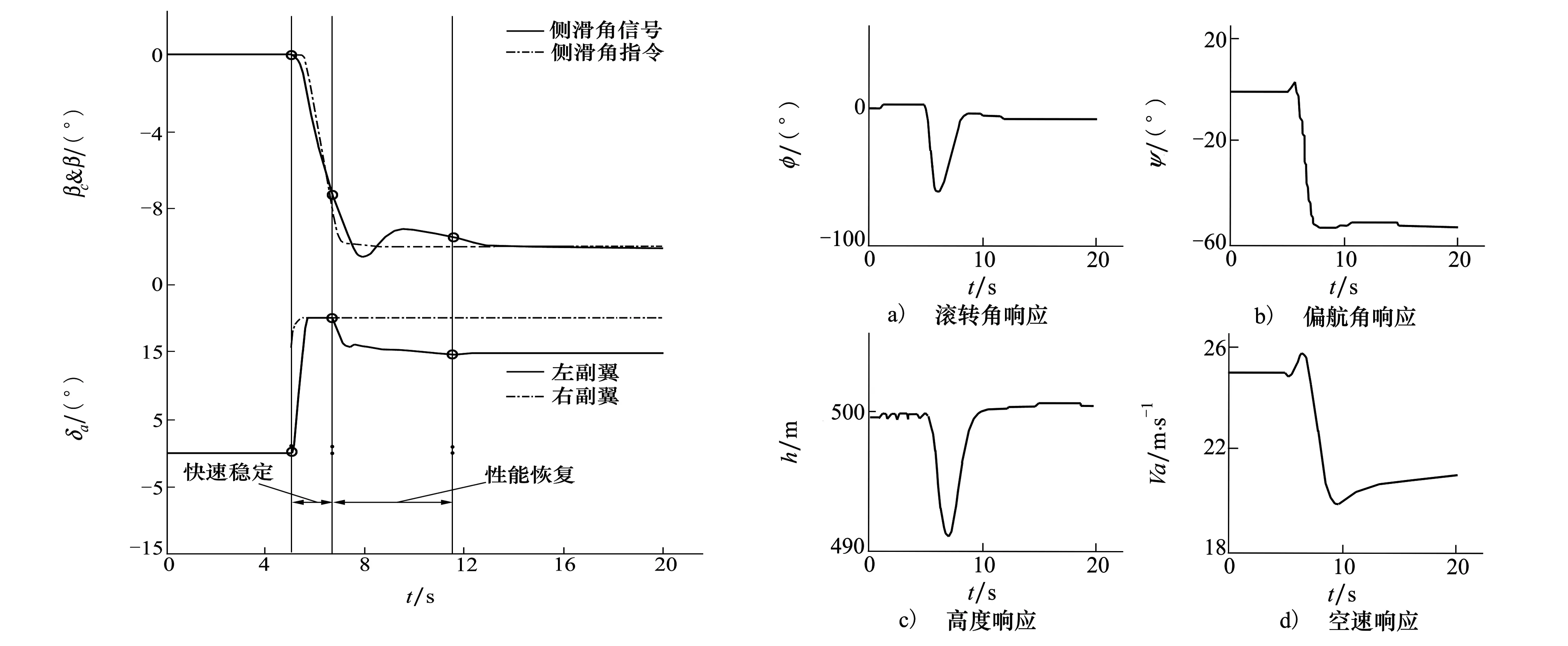
圖4 副翼及側滑角響應 圖5 其他相關量響應

從上面各圖可以看出,在5 s時右副翼開始卡死到極限位置(20°),滾轉角迅速增大到-60°,高度下降近9 m,航向變化近50°,飛機有盤旋下降的趨勢,在自適應指令生成器的作用下,左副翼也迅速出舵到極限位置,在2 s內使滾轉角回到20°以內,同時高度開始上升;在滾轉角和高度開始回歸后,側滑角指令逐漸增加,左副翼出舵量從極限值(20°)開始減小,最后減小到15°之內,側滑角穩定在10°,同時滾轉角和航向角以及高度都穩定下來,飛機保持一個固定的側滑角水平直飛,整個過程在4 s內基本穩定下來。

4 結 論

本文通過引入側滑角產生額外的滾轉力矩,來進行飛機單側副翼極限位置卡死時的容錯控制。相比于現有的只能處理單側副翼有限卡死的容錯控制方案,該方法的容錯能力大幅提高。本文設計的指令生成器和側滑角控制律使用經典的PID控制結構,簡單直觀,易于調參和工程實現。仿真結果表明,本文提出的方案能使飛機在單側副翼極限位置卡死后快速穩定下來,并逐漸恢復未卡死副翼的操縱能力。

參考文獻：

[1] 王娜,席劍輝,黃宇,趙文成. 無人機單副翼有限卡死時荷蘭滾運動分析[J]. 儀器儀表學報,2009,30(6):838-842

Wang Na, Xi Jianhui, Huang Yu, Zhao Wencheng. Analysis on Dutch Roll Modal of Unmanned Aerial Vehicle with the Limited Deadlocking of Single Aileron[J]. Chinese Journal of Scientific Instrument, 2009,30(6):838-842 (in Chinese)

[2] 張平,陳宗基. 飛機操縱面故障研究及其補償重構[J]. 飛行力學,1997,15(3):67-72

Zhang Ping, Chen Zongji. Aircraft Failures Studies and Its Reconfigurable Control[J]. Flight Dynamics, 1997, 15(3):67-72 (in Chinese)

[3] Bajpai G. Reconfigurable Control of Aircraft Undergoing Sensor and Actuator Failure[D]. Drexel University, Philadelphia, 2002

[4] Thomas Suba, Kwatny Harry G, Chang Bor-Chin, et al. Regulator Design for Control Surface Failure Accommodation in an F-16[C]∥AIAA Guidance, Navigation, and Control Conference, 2005

[5] Jourdan D B, Piedmonte M D, Gavrilets V, et al. Enhancing UAV Survivability through Damage Tolerant Control[C]∥AIAA Guidance, Navigation, and Control Conference, 2010: 2-5