衰落信道下空時編碼級聯RS碼的性能分析與研究

包濤, 梁永玲

(1.西北工業大學 電子信息學院, 陜西 西安 710129; 2.中國刑事警察學院刑偵系, 遼寧 沈陽 110035)

未來無線通信系統要求能夠以可靠的通信質量提供包括語音、圖像等多媒體在內的多種業務，這對系統的信道容量提出很高的要求。空時編碼技術是一種獲得MIMO系統容量，提高通信質量的可行技術，它采用多個發送天線和接收天線傳送信息，可以在不犧牲帶寬的情況下，帶來分集和編碼增益，提高無線衰落信道的傳輸性能。其中，空時分組碼STBC是Alamouti等人提出的一種簡單空時編碼。非二進制RS碼是一種最大距離可分碼，尤其適用于存在突發錯誤的信道。而多徑衰落和時變特性使得無線信道中的突發錯誤比較突出。針對這一現象，本文首先通過公式定量地分析了在獨立同分布信道下具有滿分集度的空時編碼在瑞利衰落情況下的性能衰減情況，而后根據公式和空時編碼準則，提出了一種穩健的編碼結構，將一個滿秩的空時編碼模塊和外碼RS碼級聯，仿真結果表明這種結構在一定程度上彌補了空時碼在衰落信道下編碼增益的損失，降低了誤碼率，在信噪比較大時其優越性更為顯著。

1 衰落信道模型

考慮到大部分的無線傳輸系統采用以載波頻率fc為中心的帶通傳輸。因此，信道可用時變沖擊響應來描述，即在時刻t，信道對t-τ時刻作用的脈沖時域響應，也可以用頻域的時變頻率響應來描述。

對于平坦衰落信道，在時刻k時的接收信號y(t)在數學上可以表示成

(1)

式中:x(k)代表第k個發射符號；h(k)代表對應于此符號的衰落信道系數；n(k)是零均值的加性復高斯白噪聲項。假設E[|h(k)|2]=1，表示信號的平均功率已歸一化，且噪聲項的均值為零，每個維度的方差為1/2，則ρ可以視為接收機的平均信噪比。隨機信道增益的分布取決于特定的信道模型。

由(1)式知，無線信道對發射信號的作用表現為乘積關系，乘積項是一個復高斯隨機變量。如果信道系數的均值為零，此時信道增益的絕對值是一個瑞利隨機變量，因此這種信道稱為瑞利衰落信道；如果信道增益的均值不為零，其絕對值是萊斯分布的，那么稱信道為萊斯衰落信道。

用一個復數隨機變量h表示信道增益，|h|表示信道增益的絕對值，φ=∠h表示信道的相位。對于瑞利衰落信道，|h|的概率密度函數(probability density function, PDF)可表示為

(2)

式中:Pr代表由于路徑損耗和陰影效應的平均信道功率；φ是一個在區間(0,2π)內的均勻分布隨機變量。

對于萊斯衰落信道，信道包絡的PDF為

(3)

式中:I0(·)表示零階第一類修正貝賽爾函數；K為萊斯因子，它表示信道中視距(line of sight, LOS)路徑(或稱鏡面反射路徑)的功率與散射傳播分量功率的比值。顯然，如果K=0，得到瑞利衰落，即沒有LOS分量；如果K→∞，由于此時沒有散射傳播分量，則得到簡單的AWGN信道(具有恒定的信道增益)。在這種情況下，信道增益的相位不是均勻分布的。

2 級聯碼的結構

通信系統中需要一種功能強大的碼，以滿足對高質量通信的要求。級聯編碼便是一種產生這種碼的實用技術。它將2個或多個碼級聯，使總碼長增加，從而得到優異的性能，同時并沒有增加系統硬件的復雜度[1]。以2級級聯為例，級聯碼的一般結構如圖1所示[2]。

圖1 級聯碼實現方框圖

由數據源來的符號首先進入的編碼器稱為外碼編碼器，輸出(n,k)的外碼，外碼是非二進制碼，每個符號由K比特組成。這些符號由外碼編碼器輸出后又進入內碼編碼器。再次編碼后，每個符號被編碼成(N,K)的內碼，內碼是二進制碼，這些碼字被送入信道。在接收端，碼字并行進入內碼譯碼器，內碼譯碼器的功能是以較低的誤符號率Ps輸出外碼符號，而外碼譯碼器則進一步糾正盡可能多的錯誤，得到更低的誤比特率Pb。由此得到的級聯碼總長為N′=N×nbit，其中信息位為K′=K×kbit。這樣，級聯碼的編碼效率為R′=R×r=(K×k)/(N×n)。由于譯碼工作由針對碼長為N和n的2個譯碼器分別完成。因此，與要得到同樣錯誤率所需的單級譯碼器相比，系統的復雜性大大降低。

通過選擇不同的內碼和外碼可以使級聯有不同的配置方案。本文所構建的配置方案為在發送端，信息序列首先進入外碼編碼器(RS碼)，輸出非二進制的RS外碼符號，然后再進入內碼編碼器(STBC碼)，輸出二進制的STBC內碼符號，最后再送入天線分集發送。在接收端，接收到的信息序列先進入內碼譯碼器解碼STBC碼，然后再進入外碼譯碼器解碼RS碼，最后送判決器進行判決輸出。

3 級聯碼系統性能的理論分析

3.1 RS碼的誤比特率性能分析

假定系統采用RS碼作外碼，此時內碼譯碼器只需輸出符號判決，而不需提供符號刪除或有關符號可靠性的信息。這樣，若內碼譯碼器輸出誤符號率為Ps，則對一個能糾t個符號錯誤的(n,k)RS碼來說，譯碼后輸出的誤比特率Pb具有如下上限[3]

(4)

這樣，由特定內碼的輸出誤符號率Ps即可估計出級聯碼的輸出誤比特率Pb的上限。

3.2 STBC碼的誤符號率性能分析

1) 瑞利衰落信道

瑞利衰落信道下，復信道衰落系數hi,j是均值為0，方差為δ2的獨立復高斯隨機變量，其幅度成瑞利分布，概率密度為

(5)

由序列hi,j的獨立性假設，通過簡單積分運算即可得到瑞利衰落下平均誤符號率(symbol error rate, SER)的最小距離球界為[4]

(6)

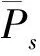
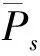
(7)

此時，由公式(7)得到了STBC碼在瑞利衰落信道下單級編碼的性能。

2) 萊斯衰落信道

在萊斯信道中，復信道hi,j的幅度|hi,j|服從萊斯分布，即有概率密度函數[5]

(8)

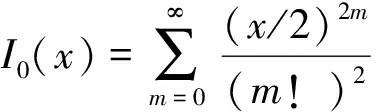
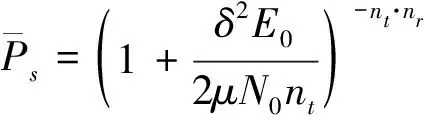
(9)

當給定接收天線數nr時，若發送天線數ns→∞，則(9)式變為

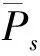
(10)

綜上所述，將公式(4)、(7)式和(10)式相結合，即可得到級聯碼的誤比特率性能。

4 系統仿真結果及分析

不失一般性，考慮衰落信道條件下NT=2幅發送天線，NR=1幅接收天線的無線傳輸系統。設第i幅發送天線到第j幅接收天線的衰落系數為hiu,j(t)(i=1,2,…,nt;j=1,2,…,nr)，在傳送一個STBC符號的時間 內信道衰落系數hi,j(t)恒定，即hi,j(t)=hi,j(t+T)，且在接收端已準確得到。

作為外碼的RS糾錯編碼的運算是建立在GF基礎之上，它是由有限個元素與相應定義的加法、乘法組成的域，表示為GF(2m)。對于RS(7,3)碼，每個信息的比特數m=3，碼長n-k=4，信息符號位長k=3，校驗符號位長n-k=4，糾錯能力t=(n-k)/2=2，碼距d=2t+5，本原多項式為P(x)=x2+x+1。對于RS(15,9)碼，每個信息的比特數m=4，碼長n=2m-1=15，信息符號位長k=9，校驗符號位長n-k=6，糾錯能力t=(n-k)/2=3，碼距d=2t+1=7，本原多項式為P(x)=x4+x+1。對于RS(255,223)碼，每個信息的比特數m=8，碼長n=2m-1=255，信息符號位長k=223，校驗符號位長n-k=32，糾錯能力t=(n-k)/2=16，碼距d=2t+1=33，本原多項式為P(x)=x2+x7+x2+x+1。作為內碼的STBC碼選用生成多項式為(11)式的Alamouti碼[6]。

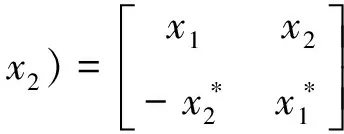
(11)

圖2給出了瑞利衰落信道條件下采用8PSK調制方式時STBC碼和STBC碼與RS(7,3)、RS(15,9)、RS(255,223)碼級聯時系統的誤比特率性能比較。瑞利衰落模型適用于描述建筑物密集的城鎮中心地帶的無線信道。密集的建筑和其他物體使得無線設備的發射機和接收機之間沒有直射路徑，而且使得無線信號被衰減、反射、折射、衍射。而在城市微蜂窩、衛星移動通信等系統中，由于信源和信宿之間可能存在可視路徑傳播信號，直射波分量不可忽略。此時，萊斯信道假設比瑞利假設更接近實際信道。圖3則表征的是萊斯衰落信道下不同糾錯能力的RS碼級聯STBC碼的誤比特率性能曲線。萊斯衰落信道下的誤比特率性能曲線與瑞利衰落時相比較，結果與瑞利衰落模型相類似，但萊斯衰落下交叉點的SNR值較小。如圖2和圖3所示，瑞利和萊斯衰落下交叉點的SNR值分別約為16 dB和12 dB。這是因為在萊斯衰落下存在直射路徑，信道較好，所以交叉點對應的SNR值也相對較小，即信道質量越好，交叉點對應的SNR值越小。

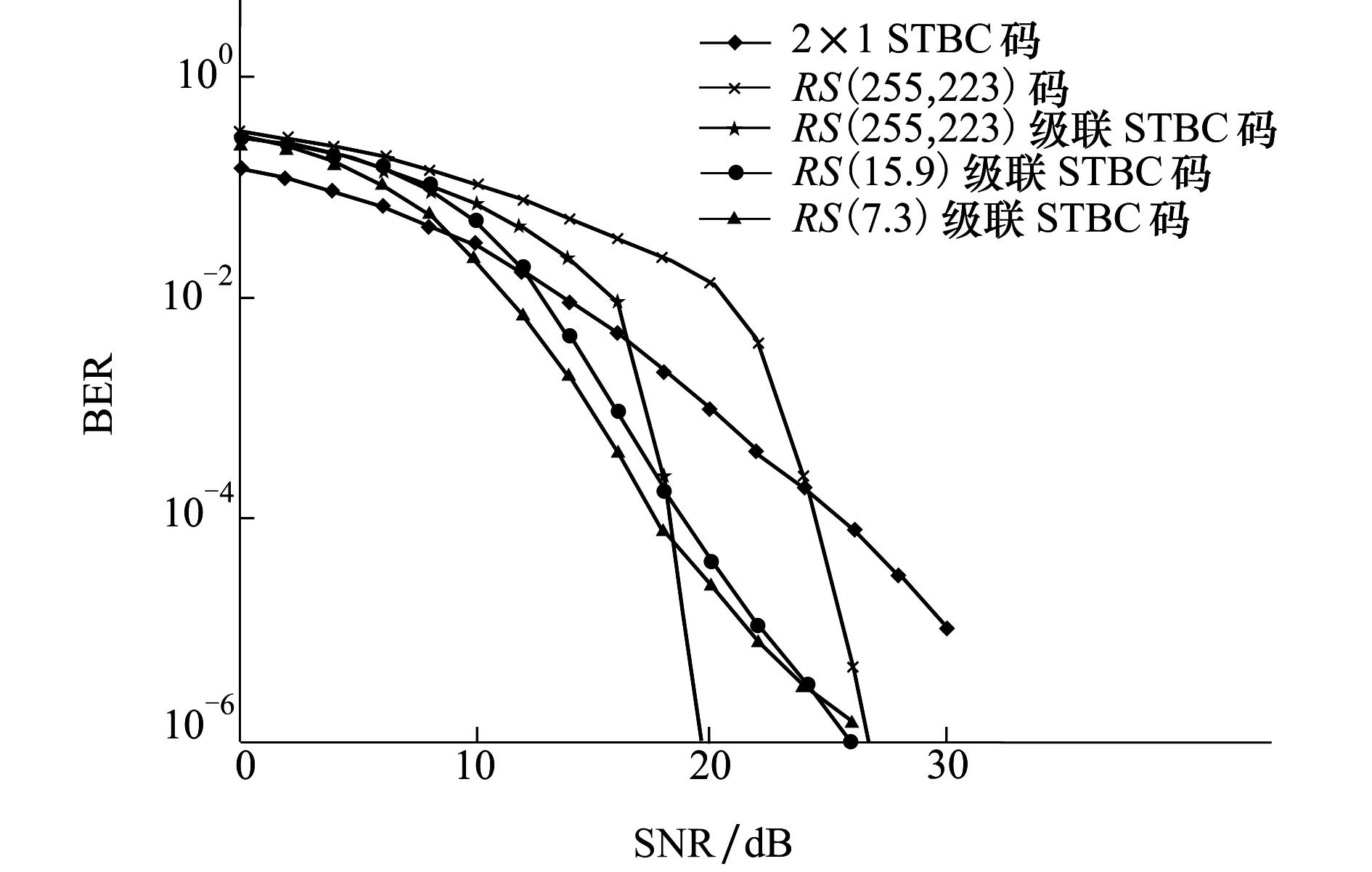
圖2 瑞利衰落下采用8PSK調制時STBC與不同RS碼級聯的差錯性能比較

圖3 萊斯衰落下采用8PSK調制時STBC與不同RS碼級聯的差錯性能比較

觀察圖4、圖5和圖6得出，不同的調制方式，級聯碼性能急劇下降的交叉點所對應的SNR值也不同。BPSK調制方式下交叉點對應的SNR值為9 dB，QPSK調制方式下對應的值為12 dB，8PSK調制方式下對應的值為16 dB，16QAM調制方式下對應的值為22 dB，即星座點之間的距離越小，所對應的SNR值則相對越大。這是因為，在信噪比較低的情況下，16QAM與8PSK、QPSK和BPSK調制方式相比，星座點的誤判率大，從而造成了誤比特率性能的下降。隨著信噪比的提升，接收信號星座圖中的星座點更加收斂于發射信號中的星座點，因此誤判概率下降，誤比特率性能顯著提升。

圖4 瑞利衰落下采用BPSK調制時STBC與不同RS碼級聯的差錯性能比較 圖5 瑞利衰落下采用QPSK調制時STBC與不同RS碼級聯的差錯性能比較 圖6 瑞利衰落下采用16QAM調制時STBC與不同RS碼級聯的差錯性能比較

圖7為瑞利衰落信道環境下，采用不同發射/接收天線時空時分組碼與RS(255,223)碼級聯在8PSK調制方式下誤比特率性能比較的仿真結果圖。

圖7 瑞利衰落下采用不同發射/接收數天線時級聯碼的差錯性能比較

由空時碼理論研究知[7]，空時分組碼可實現全分集增益，且此時的分集增益為發射與接收天線數的乘積。而與RS(255,223)碼的級聯，又帶來了很大的編碼增益。因此，從仿真圖中可見，2發2收的級聯碼具有很好的誤比特率性能，且在信噪比大于11 dB時，性能開始迅速變好，相比于2發1收的級聯碼，性能增益提升了大約6 dB。

5 結 論

本文提出一種穩健的編碼結構，采用RS碼與STBC碼級聯，仿真證明了級聯方式彌補了單一空時碼或RS碼在衰落信道中性能的惡化。在此基礎上，比較了在不同衰落信道、調制方式、發送/接收天線數、空時分組編碼矩陣和RS碼參數的情況下，應用該級聯編碼結構時性能的改善情況。仿真結果顯示這種結構在一定程度上彌補了空時碼在衰落信道下的分集增益和編碼增益的損失，降低了誤碼率，尤其在信噪比較大時其優越性更為顯著。

參考文獻：

[1] Zuo J, Hung V N, Soon X N. Energy-Efficient Relay Aided Ad Hoc Networks Using Iteratively Detected Irregular Convolutional Coded, Unity-Rate Coded and Space-Time Trellis Coded Transceivers[C]∥Proc IEEE′WCNC, 2011: 1179-1184

[2] Liew T H, Hanzo L. Space-Time Codes and Concatenated Channel Codes for Wireless Communications[C]∥Proc IEEE′JPROC, 2002:185-186

[3] Luo T, Hao J J, Li X M. A Theoretical Method of Performance Estimate for Reed-Solomon Codes Concatenated Space-Time Block Codes[J]. Journal of China Universities of Posts and Telecommunications, 2002, 9(1): 302-304

[4] Amah A U T, Klein A. Non-Regenerative Multi-Way Relaying: Space-Time Analog Network Coding and Repetition[J]. IEEE Commun Lett, 2011, 15(12): 1362-1364

[5] Yan Z H, Lu Y L, Ma M D. Decoding of QOSTBC Concatenates RS Code Using Parallel Interference Cancellation[C]∥Proc IEEE′ICDIP, 2010

[6] Tarokh V, Seshadri N, Calderbank A R. Space-Time Codes for High Data Rate Wireless Communication: Performance Criterion and Code Construction[J]. IEEE Trans on Inform Theory, 1998, 44(3): 744-765

[7] Alamouti S M. A Simple Transmit Diversity Technique for Wireless Communications[J]. IEEE J Select Areas Commun, 1998, 16(10): 1451-1458

[8] Niu B, Beluri M C, Lin Z. Relay Assisted Cooperative OSTBC Communication with SNR Imbalance and Channel Estimation Errors[C]∥Proc IEEE′VTC, 2009: 950-954