斜齒輪齒向修形對承載能力的影響

楊 柯，李友榮，曾義斌，張伊波

(1.武漢科技大學冶金裝備及其控制教育部重點實驗室，湖北 武漢，430081;2.武漢鋼鐵股份有限公司設備維修總廠，湖北 武漢，430083)

某鋼廠1580熱連軋機主傳動系統采用斜齒輪傳動方式，該齒輪由于尺寸大、承受重載、工作環境惡劣、不間斷工作時間長等因素的影響，曾出現齒面劃傷甚至斷齒的事故，嚴重影響軋機的正常生產。為提高齒輪承載能力，保證軋機安全穩定運行，有必要對斜齒輪副進行強度分析。本文以該熱連軋機F1軋機主減速機斜齒輪副為研究對象，建立其三維模型，利用有限元軟件分析計算齒輪的應力分布情況，并進行強度校核，找出故障產生的原因，結合齒輪齒向修形理論提出最佳修形方案，以期減少齒輪在接觸狀態下的應力集中，提高減速機斜齒輪傳動的承載能力。

1 斜齒輪參數化模型

斜齒輪屬于標準件，當法面模數、齒數和螺旋角已知時，其他各幾何尺寸可以通過幾何關系計算而得。

表1所示為斜齒輪的基本參數。根據表1參數，在Pro/E中通過輸入方程添加關系的方式會自動生成齒輪其他部分的相應尺寸[1]，最終得到無干涉齒輪的裝配模型，如圖1所示。將得到的模型保存為IGS格式，即可導入到有限元程序中進行仿真分析。

表1 斜齒輪副基本參數Table 1 Basic parameters of the helical gear

圖1 齒輪裝配圖Fig.1 Assembly drawing of gears

2 齒輪有限元仿真分析

2.1 定義材料屬性

大小齒輪的材料均為17Cr2Ni2Mo，齒面采用滲碳淬火處理，硬度為56～61HRC，泊松比μ=0.3，彈性模量E=207 GPa。

2.2 網格劃分

采用自由網格劃分,小齒輪的單元尺度設置為50 mm,大齒輪的單元尺度設置為100 mm。為了保證得到的結果更為準確，對局部網格進行細化，即選取齒輪嚙合過程中可能會接觸的面，設置其單元尺度為10 mm。摩擦系數取為0.1。

2.3 添加約束和載荷

(1)約束。大齒輪軸輸出端全約束，輸入端只能繞軸向轉動。小齒輪軸徑向和水平方向約束，使其只能繞軸向轉動。

(2)載荷。在小齒輪輸入端施加一個逆時針方向的扭矩，其值取為該減速機的額定輸入扭矩T=424.44 kN·m。

2.4 子模型分析計算

由于該齒輪副整體結構尺寸很大，在較小的網格密度下計算機計算效率低，較大的網格密度下得到的結果又不夠精確，故采用子模型分析方法，將輪齒嚙合區從整體模型中切割出來重新計算。子模型縱向寬度取原模型整個齒寬，徑向取與內孔距離為1.8倍端面模數的范圍。子模型方法又稱為切割邊界位移法，整體模型切割邊界的計算位移值即為子模型的邊界條件[2]。子模型單元尺度設為10 mm，輪齒接觸面單元尺度設為2 mm。以下數據皆為子模型的精確計算值。

2.5 仿真結果與分析

因齒輪副中小齒輪的應力比大齒輪大，故以下僅討論小齒輪的應力及強度。在嚙合過程中接觸中心帶是沿一條平行于齒輪軸的直線移動的。因此，為得到斜齒輪在傳動過程中不同接觸位置的應力值，選取一對嚙合齒在其接觸帶中心分別位于Z=0 mm(Z為齒寬方向坐標，Z=0 mm處即為齒輪端面)、Z=175 mm(1/4齒寬處)和Z=350 mm(齒寬中心處)時的斜齒輪模型進行接觸分析。

接觸帶中心位于Z=0 mm時，小齒輪的第一、第三主應力分布云圖以及接觸云圖分別如圖2～圖4所示。由圖2和圖3中可以看出，此時小齒輪最大應力部位在其端部齒根處，該處第一主應力最大值為384.56MPa,第三主應力值為21.4 MPa，處于三向受拉應力狀態，應按第一主應力進行強度校核。由圖4可知齒面最大接觸應力為847.23 MPa。

圖2 Z=0 mm時小齒輪的第一主應力分布云圖

Fig.2FirstprincipalstressdistributionnephogramatZ=0mmofthepinion

圖3 Z=0 mm時小齒輪的第三主應力分布云圖

Fig.3ThirdprincipalstressdistributionnephogramatZ=0mmofthepinion

圖4 Z=0 mm時小齒輪的接觸應力云圖

Fig.4ContactstressnephogramatZ=0mmofthepinion

同樣可得接觸帶中心位于Z=175 mm和Z=350 mm時的相應應力值，如表2所示。

表2不同接觸帶中心位置下齒輪的最大應力值

Table2Maximumstressvalueunderthreedifferentcontactcentersofthegear

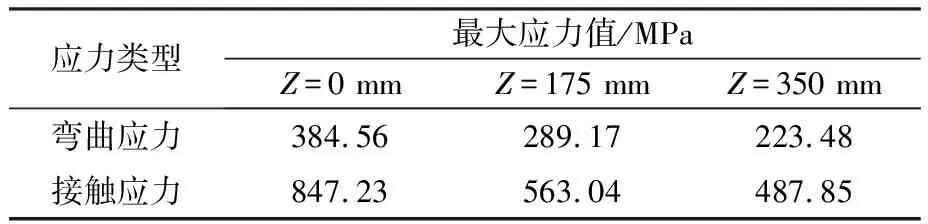
應力類型最大應力值/MPaZ=0 mmZ=175 mmZ=350 mm彎曲應力384.56289.17223.48接觸應力847.23563.04487.85

從表2中可見，在輪齒剛進入嚙合位置，即Z=0 mm時，齒輪的接觸應力和彎曲應力過大，經計算，該齒輪的接觸應力安全系數為1.33，大于最小接觸應力安全系數SHmin=1.0[3]，滿足要求，但彎曲應力安全系數為1.21，小于最小彎曲安全系數SFmin=1.25[3]，不滿足要求，因而造成齒輪的損傷，嚴重時發生輪齒端部斷裂(見圖5)。因此有必要降低接觸帶中心位于Z=0mm時齒輪的應力值。本文擬采用齒向修形的方法[4]來降低輪齒端部的應力，以提高齒輪的承載能力。

圖5 輪齒斷裂形貌Fig.5 Fracture morphology of the gear tooth

3 齒向修形后齒輪的仿真結果分析

3.1 齒向修形方法

齒輪齒向修形主要是對齒輪齒面沿齒向方向進行微量的修整[5]，使其偏離理論齒面，以改善載荷沿輪齒接觸線的不均勻分布現象，從而大大提高齒輪的承載能力。考慮到實際應用中加工難度和成本因素的影響，本文采用一種簡單的、便于實際運用的齒端修形方法，如圖6所示。

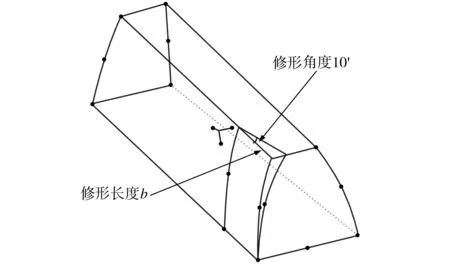
圖6 齒向修形示意圖Fig.6 Schematic diagram of modification

3.2 接觸應力分析

依據圖6建立相應的修形齒輪模型，導入到有限元軟件中進行分析。設置齒向修形長度分別為60、70、80 mm,每種修形量下取接觸帶中心位于Z=0 mm、Z=175 mm和Z=350 mm 時的齒輪應力分布云圖進行分析。

圖7所示為接觸帶中心位于Z=0 mm時，不同修形量下齒輪的接觸應力分布圖。由圖7中即可得Z=0 mm時不同修形長度下齒面的最大接觸應力值。采用同樣方法，也可獲得Z=175 mm和Z=350 mm時的相應值，結果如表3所示。

由表3中數據計算可得，與修形前相比，隨著修形長度的增加，齒面最大接觸應力在Z=0 mm和Z=175 mm時都有不同程度的降低，而在Z=350mm時其值變化不大。修形長度分別為60、70、80 mm，Z=0 mm 時齒面最大接觸應力比修形前的相應值分別降低了21.38%、27.38%和29.30%；而Z=175mm時相應的降幅分別為3.36%、5.72%和9.52%，明顯低于Z=0 mm時的降幅。

表3不同修形量及接觸帶中心位置下齒面的最大接觸應力

Table3Maximumcontactstressatdifferentmeshingpositions

b/mm最大接觸應力/MPaZ=0 mmZ=175 mmZ=350 mm0847.23563.04487.8560666.07544.87497.4570615.24531.61503.0180598.96510.16495.29

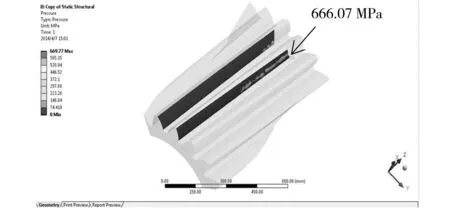
(a)b=60 mm

(b)b=70 mm

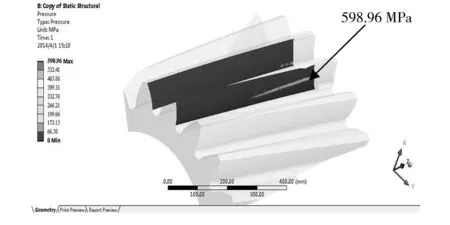
(c)b=80 mm

圖7Z=0mm時不同修形長度下齒面的接觸應力云圖

Fig.7ContactstressdistributionnephogramofthepinionatZ=0mm

3.3 彎曲應力分析

圖8所示為接觸帶中心位于Z=0 mm時，不同齒向修形長度下修形后齒輪的彎曲應力分布圖。

將圖8與圖3對比可以發現，齒向修形后，齒輪彎曲應力最大值區域偏離齒根端部一定距離，顯著地降低了齒根端部的應力值，可避免由于齒根端部應力值過大而產生的輪齒斷裂[6]。采用同樣方法可得Z=175 mm和Z=350 mm時齒根的最大彎曲應力。取3種修形量下接觸帶中心位于不同位置時齒根的最大彎曲應力值列于表4。

由表4中可見，與未修形時相比，不同修形長度下修形后齒根最大彎曲應力在接觸帶中心位于Z=0 mm和Z=175 mm時有著不同程度的變化，而位于Z=350 mm時卻變化不大，修形 長度為60、70、80mm時,Z=0mm時其降幅分別為16.85%、21.66%和22.40%；Z=175 mm時其降幅分別為8.6%、11.01%和12.75%。

(a)b=60 mm

(b)b=70 mm

(c)b=80 mm

圖8Z=0mm時不同修形長度下修形后齒輪的彎曲應力云圖

Fig.8BendingstressnephogramofthegearatZ=0mm

表4不同修形量及接觸帶中心位置下齒根的最大彎曲應力

Table 4 Maximum bending stress of root at different locations

3.4 最佳修行量的確定

綜上分析可知，齒向修形長度量為80 mm時，齒面最大接觸應力和齒根最大彎曲應力降幅最大，改善齒輪承載能力的效果最明顯，故理論上最佳修行量應為80 mm,但在實際生產中，要在減速機斜齒輪上修形80 mm，其費用要比修形70 mm時高很多，而這兩種修形量下齒輪所受應力的降幅相近，修形70 mm時已經能夠滿足要求。綜合考慮，選取70 mm為實際最佳齒向修形長度。

4 結論

(1)斜齒輪在剛進入嚙合的時候，其齒面接觸應力和齒根彎曲應力值過大，是造成輪齒劃傷、磨損甚至斷裂的主要原因。

(2)齒向修形能夠在很大程度上降低齒輪嚙合過程中的最大應力值，明顯提高齒輪的承載能力。

(3)某鋼廠1580熱連軋機主減速機最佳齒向修形長度確定為70 mm，不但能夠滿足提高齒輪承載能力的要求，而且降低了加工成本。

[1] 楊生華.齒輪接觸有限元分析[J].計算力學學報，2003, 20(2)：189-194.

[2] 田涌濤,李從心,佟維，等.基于子結構技術的復雜齒輪系統有限元三維接觸分析[J].機械工程學報, 2002,38(5):133-137.

[3] 吳宗澤.機械設計師手冊(上冊)[M]. 北京: 機械工業出版社, 2002.

[4] 潘洪鑫.齒輪修形技術研究[J].中國新技術新產品，2011(13):122.

[5] 呂少炯.漸開線圓柱齒輪修形及其對傳動性能影響的研究[D]. 南京:南京航空航天大學，2010.

[6] Giorgio Bonori,Marco Barbieri,Francesco Pellicano.Optimum profile modifications of spur gears by means of genetic algorithms[J].Journal of Sound and Vibration, 2008, 313(3-5): 603-616．