基于模糊控制的RBF神經網絡電力系統短期負荷預測

崔艷艷，程亞維

(濟源職業技術學院a.電氣工程系;b.信息工程系，河南濟源 459000)

0 前言

近年來隨著競爭機制的不斷引入，我國的電力系統正由壟斷經營階段逐步向發電競爭階段過渡，負荷預測工作也隨之逐步發生轉變［1］。負荷預測的重要性已經得到普遍重視，負荷預測的手段已由先前的人工預測方式逐步被軟件預測方式所代替，負荷預測軟件己成為能量管理系統(EMS)的重要組成部分［2］。另外，由于計算機的普及，使大量適用于電力市場環境下的負荷預測理論算法和預測模型的采用成為可能，為提高預測精度創造了有利條件。

目前，短期負荷預測的方法有很多種，神經網絡和模糊理論預測方法受到國內外廣大研究人員的高度重視，被認為是比較有效的方法［3］。在此背景下，本文針對電力系統短期負荷預測系統中的各種問題，進行了深入的探討，建立基于模糊控制理論和RBF神經網絡相結合的短期負荷預測模型，并對歷史負荷數據及影響負荷的因素進行處理，通過實例驗證了該預測模型的準確性。

1 RBF神經網絡結構

徑向基函數(Radial Basis Function，RBF)神經網絡結構包括3層，依次按左、中、右的順序分別為輸入節點、隱節點、輸出點，其網絡結構如圖1所示。每一層都有著完全不同的作用:輸入層由信號源節點構成，其作用只是接受輸入信號并將其傳遞到隱含層;隱含層由像高斯核函數那樣的輻射狀作用函數構成，是RBF網絡中最重要的一層;輸出層通常是對隱含層節點非線性基函數輸出的線性組合，從而得到最后的結果［4－5］。

對于RBF網絡的數學描述可表達為:在n維空間中，給定N個輸入樣本xi=(i=1，2，…，N)，則網絡隱含層的第k個節點的輸出可以表示為:

其中，xi表示有n維輸入向量;Tk表示第k個隱層節點的中心，k=1，2，…，l;· 通常為歐式范數; R(·)也表示RBF函數，它具有局部感受的特性，體現了RBF網絡的非線性映射能力。而網絡輸出層的第j個節點的輸出，則為隱含層節點到輸出層的線性映射，即:

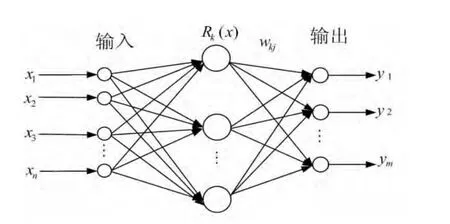
圖1 RBF網絡結構圖

其中，wkj表示隱含層到輸出層的權值;θj是第j個輸出節點的閾值;m則是輸出層的節點數。

2 基于模糊控制的RBF神經網絡電力系統短期負荷算法

隨著電力系統負荷的變化，RBF神經網絡的內在關系也應發生變化，如果用原有的神經元網絡參數進行負荷預測時，往往會產生較大的誤差，但是模糊調整可以改變這種現象，提高負荷預測的精度。本文在進行電力系統短期負荷預測時，可以在RBF神經網絡預測基礎上再進行一個在線自調整的模糊控制。假設RBF神經網絡的輸出為U，模糊調整的輸出為ΔU，則該網絡預測的最后輸出是Y=U+ ΔU，其預測流程如圖2所示。

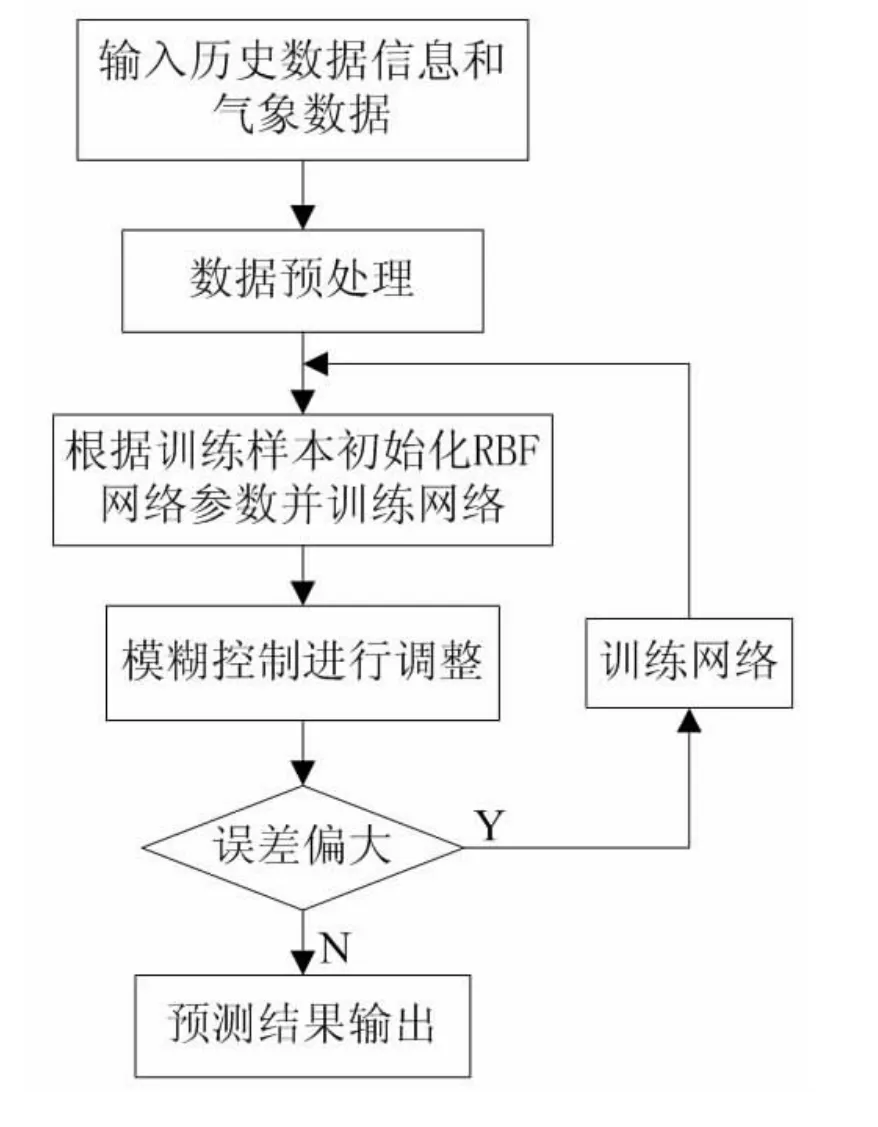
圖2 模糊控制RBF網絡預測系統工作流程

3 電力系統短期負荷預測實例分析

為了驗證該方法的有效性和精確性，選取河南省某地區某天24小時內的電力負荷進行預測。本文建立24個RBF神經網絡預測模型，每個神經網絡的輸入層節點為12個，隱含層節點為16個，輸出層節點為1個。該算法并與傳統的RBF神經網絡算法進行比較，其負荷預測曲線如圖3所示，相對誤差曲線如圖4所示。RBF和模糊控制RBF模型的預測數據進行對比，結果如表1所示。

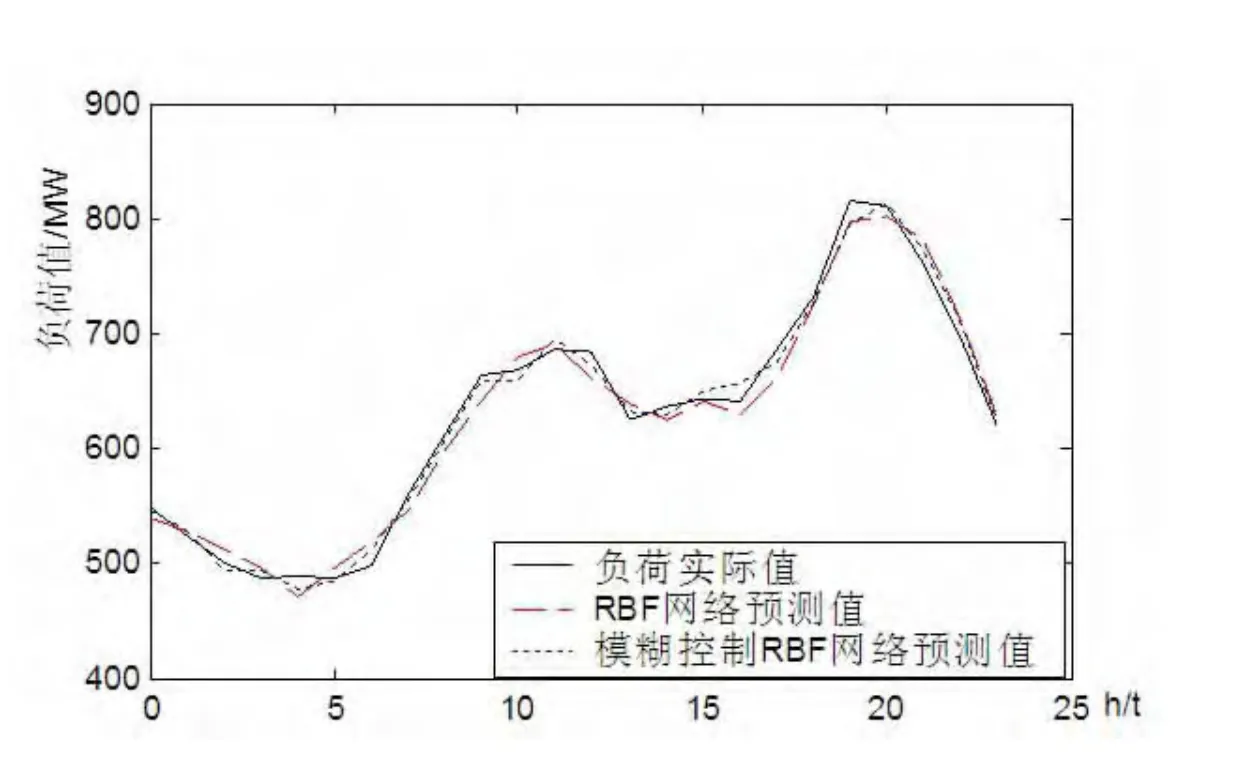
圖3 RBF和模糊控制RBF模型的負荷預測曲線

圖4 RBF和模糊控制RBF模型負荷預測相對誤差曲線

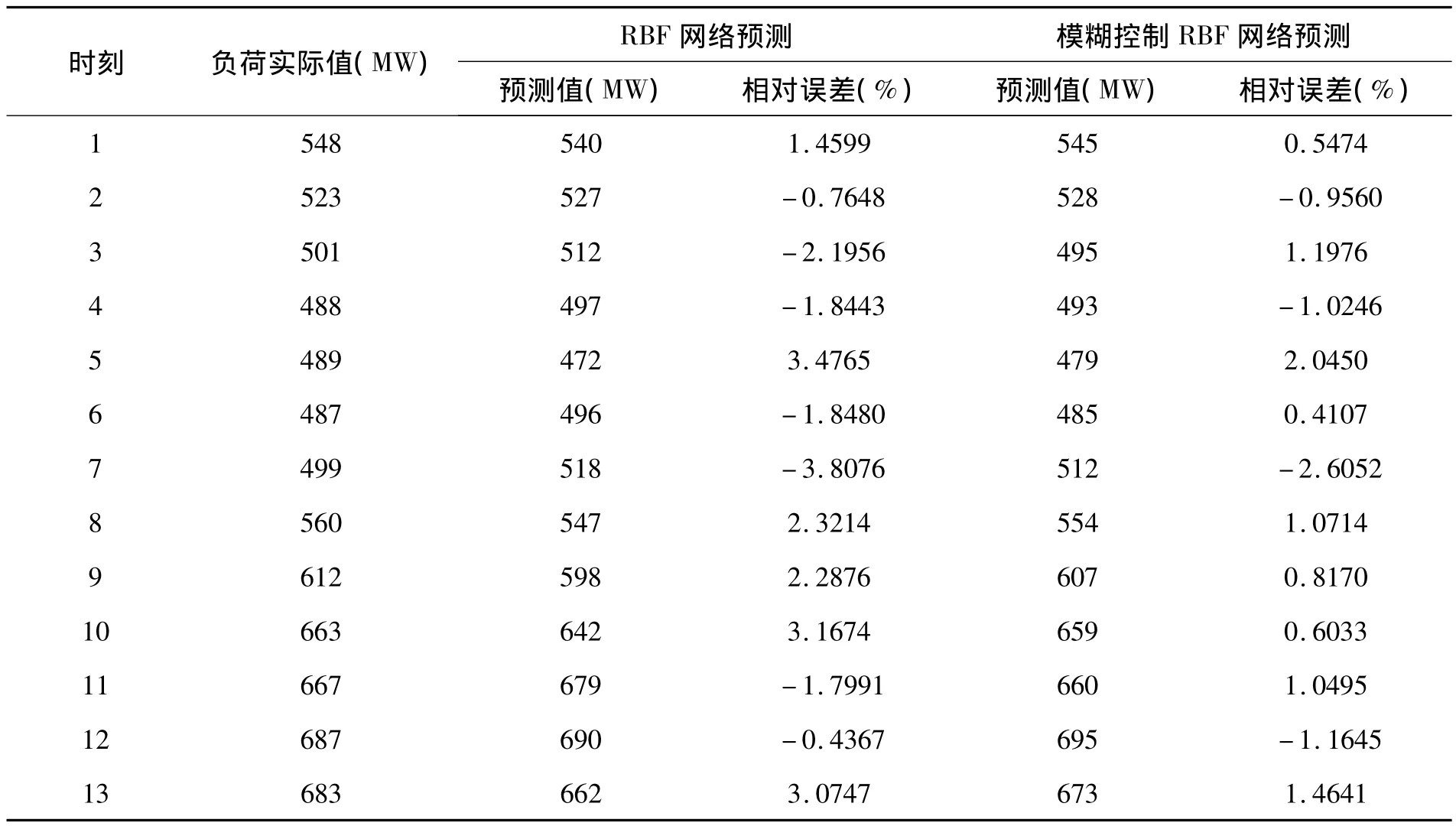
表1 RBF神經網絡和模糊控制RBF神經網絡模型的預測數據對比

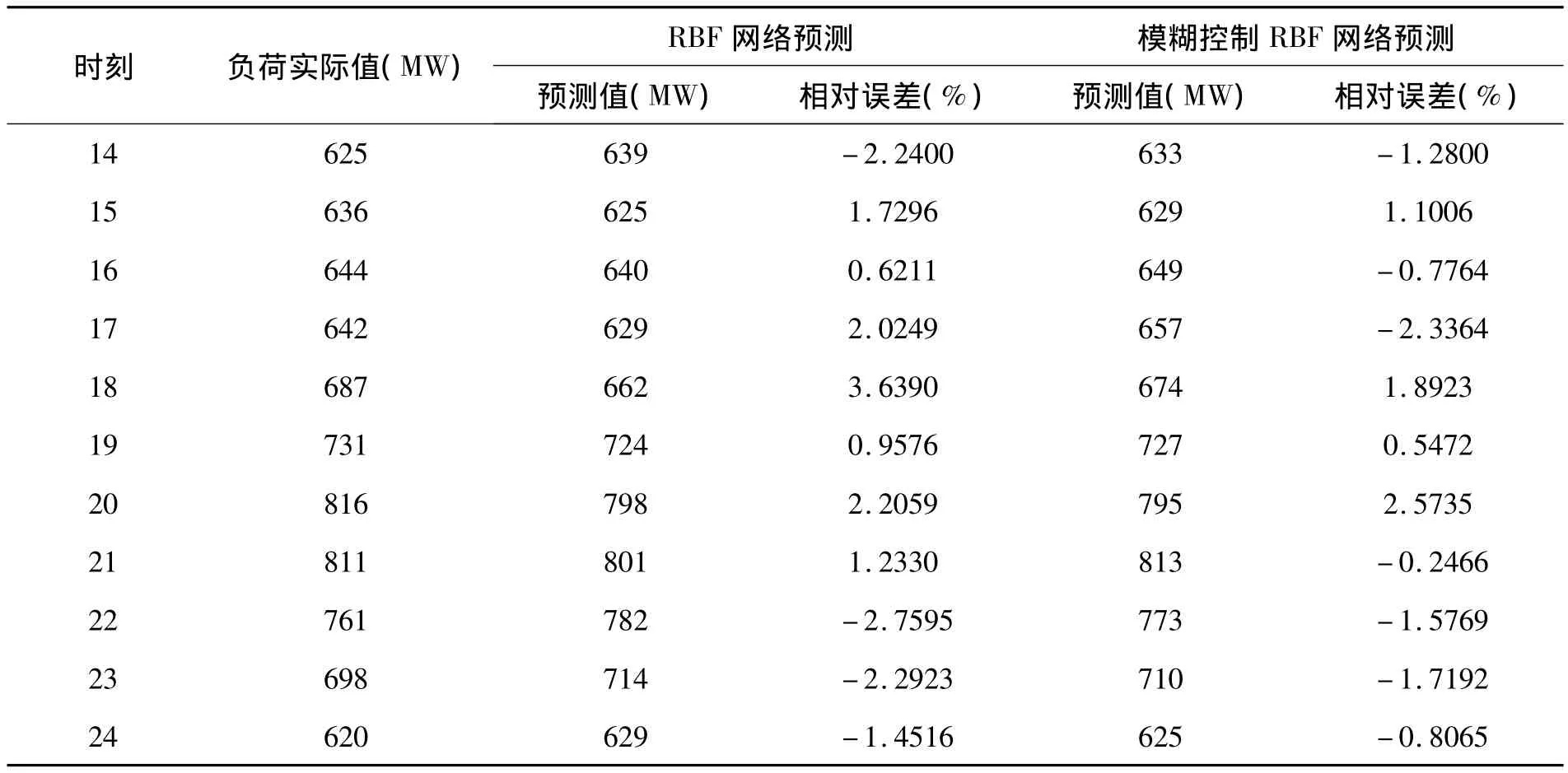
續表1

從表1中可知，RBF網絡預測的最大相對誤差為3.639 0%，最小相對誤差為－2.759 5%;而模糊控制的RBF網絡預測的最大相對誤差為2.573 5%，最小相對誤差為－2.605 2%。

4 結論

在電力系統短期負荷預測中，傳統的RBF網絡會產生較大的誤差。本文提出模糊控制與RBF神經網絡相結合的電力系統短期負荷預測算法，該算法是在RBF神經網絡預測基礎上進行在線自調整的模糊控制。結果表明，該方法與傳統的RBF神經網絡負荷預測方法相比，具有較高的預測精度。

［1］王黎明.電力系統中短期負荷預測的研究［D］.東營:中國石油大學，2008.

［2］王聰.基于RBF神經網絡與模糊控制的電力系統短期負荷預測［D］.保定:華北電力大學，2004.

［3］張寧.基于模糊推理和神經網絡的日負荷預測的研究［D］.太原:太原理工大學，2006.

［4］劉昊，張艷，高鑫，等.基于RBF神經網絡與模糊控制的短期負荷預測［J］.電網與清潔能源，2009，25(10):62－66.

［5］李楊，李曉明，黃玲，等.基于人工神經網絡和模糊集的電力系統短期負荷預測方法［J］.華中電力，2007，20(2):1－4.