城市圈互斥共生演化博弈研究

孫 銳，王源昌，李 超

(云南師范大學 數學學院，云南 昆明 650500)

20世紀80年代起，伴隨著工業化進程的不斷加速，我國的城市化進程也進入了快速發展期.進入21世紀，我國城市化進程進一步加快，城市圈大規模建設階段也已經到來.與此同時，伴隨著這場劇烈的變革，城市圈建設中不可避免的地出現了大量的經濟社會矛盾需要予以解決.而在新的城市群建設中，如何解決城市圈中城市之間錯綜復雜的關系與聯系，減少城市之間互斥，引導城市走向合作共生，成為重中之重的關鍵.

城市圈中城市的互斥與共生是一場長期的動態的博弈，而且最終達到的平衡也是一種動態的均衡.這就需要我們運用演化博弈這一新的理論去研究城市圈中的互斥共生.

1 演化博弈理論基礎

文獻[1]中定義，如果I是一個穩定策略(ESS, evolutionary stable strategy)，它必須具有下列性質：如果群體中幾乎所有個體都采取了I策略，那么采用這種策略的適應度必然將高于任何可能出現的其它策略的適應度，否則其它策略將會改變整個種群，I也就不可能穩定.假設這樣一個群體，它主要由采取I策略的個體組成，并且伴隨存在著極小比例p的采取不同策略J的個體，W0表示個體起始的適應度，W(I)和W(J)分別表示I策略和J策略所帶來的適應度；E(I,J)表示個體選擇I策略而對手選擇J策略所帶來的回報.因而有：

W(I)=W0+(1-p)E(I,I)+pE(I,J)，

(1)

W(J)=W0+(1-p)E(J,I)+pE(J,J).

(2)

由于I是ESS，那么W(I)>W(J).又因為p<<1，這就要求對所有的J≠I有：

E(I,I)>E(J,I)

或者

E(I,I)=E(J,I)，且E(I,J)=E(J,J).

(3)

這就是策略I演化穩定策略的定義.

演化博弈中博弈方策略類型的比例一直處于動態變化，博弈方通過學習模仿來調整自身的策略，通常情況下，博弈方學習模仿的速度取決于2個因素：一是模仿對象的數量大小(可用相應類型博弈方的比例來表示)，因為這關系到觀察和模仿的難易程度；二是模仿對像的成功程度(可用模仿對象策略得益超過平均得益的幅度表示)，因為這關系到判斷差異的難易程度和對模仿激勵的大小.而復制動態正是表示了某種確定策略在某群體中被采用的頻率或某個個體采用的概率變化的動態微分方程.下面給出一種復制動態微分方程的推導過程：

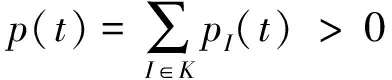
(4)

將總體平均收益表示為E(x,x)是因為這個收益與混合策略x針對自身采用時得到的收益是相同的.

假設收益代表的是博弈對個體適應性影響的增量效應，該適應性是用單位時間的后代數量來度量的.還假設，每個后代繼承了他父母的單一策略.如果生育是連續不斷的，那么按規定選擇純策略i的人們在任何時候t的出生率為β+E(i,x)，這里的β≥0是總體中人們的背景適應性(與博弈的結果無關).假設所有個體的死亡率δ是相同的.用點表示時間導數，并去掉時間自變量，就能產生如下的動態方程：

對恒等式p(t)xi(t)=pi(t)兩邊取時間的導數，得到

[β+E(i,x)-δ]pi-[β+E(x,x)-δ]pxi,

兩邊同除以p就得到

因此，對應的復制動態方程為

(5)

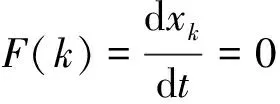
這就是動態復制微分方程的 “穩定性定理”.

接下來以演化博弈理論中的這2個基本概念為理論基礎，來進一步研究城市圈中城市間互斥共生演化博弈模型.

2 城市圈中城市間互斥共生演化博弈模型

隨著我國城市化的不斷加深，城市經濟圈的形成已經成為城市化加深的重要標志，而且在同一城市圈中的城市之間的聯系與影響也逐漸增加.由于城市圈中城市之間存在著眾多的利益沖突，每個城市為了自身利益的最大化而進行著激烈的競爭，使得城市間往往處于互斥的狀態.同時，由于存在進行分工與協作產生規模效應使合作雙方“共贏”的情況，城市圈中城市也存在合作共生的可能.在博弈的過程中，可以把城市作為一個存在有限理性的博弈方，它會根據自己以前的策略與圈內其它城市的策略來進行學習進化，從而不斷調整自己的策略.所以其選擇策略行為的過程可以視為生物學意義上的演化博弈過程，每次策略的選擇都是在考慮其他成員的策略與自身策略的適應性下做出的.因此可以用一個演化博弈模型來分析城市圈中城市互斥共生行為及其進行的動態調整.

為了方便研究，考慮兩城市之間的演化博弈模型，假設在某城市圈中存在城市A與城市B，他們之間具有一定的聯系，假設它們的策略選擇空間為互斥、共生.當城市A與城市B都采用互斥策略時(例如各自為政帶來的引資大戰、重復建設、市場分割與貿易壁壘，使城市間出現激烈競爭)，則根據各自的經濟實力與行政能力分別可以得到支付VA和VB；當城市A與城市B都采用共生策略(例如產業合作與城際分工，資源與環境合作，信息與技術的共享)，從而使兩城市達到共贏，雙方都得到在原來基礎上得到額外的收益增量W；當城市A與城市B采用的策略不同時，即一方選擇共生策略而另一方選擇互斥策略(在現實中出現這種情況往往是兩城市達成合作協議但其中一方暗中違約)，則采用互斥策略的城市能夠得到更多的收益增量Fi(i=A,B)，而采用共生策略的城市則會造成Fi(i=A,B)的損失，并假設FA

表1 不同策略下參與主體雙方的支付函數

3 演化穩定策略求解

根據上文分析，可以構建博弈雙方的收益期望函數，其中城市A采用互斥策略的期望收益為：

EA1=yVA+(1-y)(VA+FA).

而城市A采取共生策略的期望收益為：

EA2=y(VA-FA)+(1-y)(VA+W).

則城市A的平均收益為：

EA=xEA1+(1-x)EA2.

這樣根據復制動態方程，經過運算后得到城市A采取互斥策略的復制動態微分方程為：

F(x)=dx/dt=x(EA1-EA)=

x(1-x)(FA-W+Wy).

(6)

由上式對x求導得：

F′(x)=(1-2x)(FA-W+Wy).

令F(x)=dx/dt=0，解得x1=0，x2=1，y=1-FA/W.

由復制動態微分方程穩定性定理及演化穩定策略性質知，當F(x*)=0，F′(x*)<0時，x*為演化穩定策略.以下對y值進行討論：

1) 若y=1-FA/W，則F(x)=dx/dt=0，F′(x)=0，即所有y軸水平都是穩定狀態，當B城市互斥的概率達到y=1-FA/W時，城市A采取任何策略的可能性都是穩定的.

2) 若y<1-FA/W，對x1=0，x2=1，有F′(0)<0，F′(1)>0，此時x1=0為全局唯一的演化穩定策略；即當城市B采取互斥策略概率達不到一定程度并呈下降趨勢時，城市A采取互斥策略的可能性逐步減小，選擇共生策略將是城市A的最優選擇.

3) 若y>1-FA/W，對x1=0，x2=1，有F′(0)>0，F′(1)<0，此時x2=1為全局唯一的演化穩定策略；即當城市B采取互斥策略概率達到一定程度并呈增大趨勢時，城市A采取互斥策略的可能性逐步加大，最終確定為互斥策略.

城市A的復制動態相位圖如圖1所示.

同理，可以得出城市B采用互斥策略的復制動態微分方程為：

F(y)=dy/dt=x(EB1-EB)=
y(1-y)(FB-W+Wx).

(7)

由于城市B與城市A是對稱的，類似上文分析可以利用復制動態微分方程穩定性定理及演化穩定策略性質來得到類似的結果.其城市B的復制動態相位圖如圖2所示.

綜合上文城市A與城市B的復制動態相位圖，把二者結合起來，將博弈雙方的復制動態關系用一個二維的平面坐標來表示，最終得到圖3.

從圖3的二城市互斥共生演化博弈復制動態相位圖中，可以看出城市的動態演化過程.在圖3中，由點A和點C以及臨界點D構成的兩端折線，它們是使城市動態演化博弈形成兩個完全不同狀態的分界線.其中OADC區域演化博弈將收斂于O點，即相互共生；而ABCD區域的演化博弈將最終收斂于B點，即相互排斥.

從以上的演化博弈模型與復制動態相位圖可以知道，城市圈中城市的博弈可以向2個方向進行演化，既可以采取互斥策略，也可以采取共生策略，而這2種策略都是進化穩定的策略.這一結論正好可以用來解釋在現實世界中城市圈的行為.在沒有內部信任與外部約束的情況下，城市與城市政府就會傾向于考慮個體利益而不考慮集體利益，只考慮短期利益而不考慮長期利益，則必然導致城際惡性競爭并且城市間互斥的結果.而在雙方都有足夠的誠意進行合作共生，即便存在一些擾動，在多次博弈后，共生的策略也會成為唯一的穩定策略.

4 模型的參數分析與控制措施

在城市圈城市間互斥共生演化博弈策略的穩定性探討中，模型的參數變化對最終城市策略的選擇有重要的影響.在二維復制動態相位圖中可以看出，城市演化博弈過程與結果受到城市雙方初始狀態的影響.當初始狀態在OADC區域，演化博弈系統將最終收斂于O(0,0)點，即城市間將會采取相互共生策略；當初始狀態在ABCD區域時，城市雙方的演化博弈將收斂于B(1,1)點，即城市間將會采取相互排斥策略.而相同的初始狀態會因為臨界點D的變化而向不同的均衡點收斂，這是因為點D的變化會帶來上文提到的2個區域的變化，因而使得初始狀態向著不同的均衡點收斂，形成路徑不同的進化穩定狀態.

因此，可以從點D的表達式x=1-FB/W,y=1-FA/W來討論各參數變化對系統進化行為的影響和采取相應的控制措施.由于只有通過合作共生，城市圈的發展才能節能高效，長遠地可持續發展，其中的每個城市才能達到雙贏的結果.所以為了使城市間博弈最終收斂于合作共生，應該使區域OADC盡量大，即使得D點盡量接近B點.為了達到這一目的可以從兩方面入手.

4.1 參數W

參數W表示為城市圈中兩城市都采取共生策略時，給企業雙方帶來的利益的增加.當W增加時，D點坐標會向B點移動，那么區域OADC的面積隨之增大，區域ABCD的面積隨之減少，這將導致城市演化博弈以很大概率向共生穩定策略收斂.這在現實世界中表現為：當城市間采取共生合作策略所帶來的利益越大，城市間也就更趨向于合作共生.為了提高W，必須加強城市間的聯系，建立起城市間差異化產業分工、互補與合作的體系，就能夠節約生產和運輸成本，共享最新的信息與技術，從而有效利用城市圈聚集經濟和規模經濟，使得共生取得的收益達到最大.需要注意的是，在產業分工中，由于單個城市從自身利益出發，難免會有些困難與抵觸，這就需要上一級政府從戰略高度出發，統籌全局，使得各城市間職能分工明確，主導產業定位合理，實現資源優勢互補，共同提高協作共生帶來的利益.

4.2 參數FA與FB

參數FA與FB表示當城市圈中城市采取不同的策略時，采取互斥策略的城市獲得收益增加，而采取共生策略的城市的收益將減少.從表1支付可以看出同一城市采取不同策略對該城市帶來的收益增加和減少是相同的.例如當城市A采取互斥策略，而城市B采取共生策略時，FA表示城市A收益的增加，FB表示城市B收益的減少；反之，FA表示城市A收益的減少，FB表示城市B收益的增加.隨之FA與FB的增加，D點坐標會向原點O點移動，那么區域OADC的面積隨之減小，區域ABCD的面積隨之增加，那么城市雙方將極大可能采取互斥策略為進化穩定策略，這在現實世界中表現為:在城市達成共生合作的合約后，如果違約一方將能得到足夠大的利益，而守約一方將因為對方違約遭到巨大損失，那么違約方將極大可能鋌而走險繼續違約，而守約方也終將放棄合約.而隨著FA與FB的減小，D點坐標會向原點B點移動，那么區域OADC的面積隨之增大，區域ABCD的面積隨之減小，那么極大可能城市雙方將采取共生策略為進化穩定策略.即為了使城市圈中的城市能夠長期穩定的共生合作，城市雙方應該簽訂有約束的協議，并由上一級政府進行監督執行，即對違約一方進行嚴厲懲罰，盡量減少其通過違約帶來的收益；而對守約一方進行物質激勵，減小其損失，這樣就同時減小參數FA與FB的值，從而使得城市雙方達到合作共生的穩定結果.

4.3 博弈雙方的控制

在圖3中，由點A和點C以及臨界點D構成的兩端折線是使城市動態演化博弈指向2個不同結果的分界線.當已知A城市的采取互斥策略的概率x，可以根據分界線推出B城市采取互斥策略的y的范圍，使得最終城市走向合作共生.

用“兩點式”求出線段方程為

(8)

當城市A采取互斥策略的概率確定為PA，如何確定城市B采取互斥策略的概率PB取值的范圍，使雙方最終收斂于合作共生的結果.下面進行討論：

1) 當0≤PA<1-FA/W時，B城市互斥策略的概率為PB∈[0,-PAFA/(W-FB)+1)，最終可以在經過一段時間博弈后最終達成城市間的共生.

2) 當1-FA/W

5 結語

我國經濟發展與城市化建設的長期性與艱巨性決定了建設城市圈合作共生機制的重要性.運用演化博弈的基本理論對城市的策略行為進行分析，得出了影響城市進行互斥還是共生的關鍵是合作共生產生的額外收益的大小，和違反合作協約時的收益與損失的大小.這要求上級政府和城市圈中的城市統籌安排，擴大合作收益，建立良好的信用機制，對違約行為進行有效懲罰制止.并且通過了解博弈對方的合作意圖，來調整自身的策略也是達到合作共生的關鍵，這就要求城市間加強聯系，減少誤判，基于此構建的演化穩定策略也終將實現區域城市圈間的合作與共生.

參考文獻:

[1] SMITH J M, PRICE G R. The logic of animal conflicts[J].Nature，1973, 246: 15-18.

[2] SMITH J M. Evolution and the theory of games[M].Cambridge:Cambridge University Press, 1982.

[3] MAYNARD SMITH J. The theory of games and the evolution of animal conflicts[J]. Journal of Theoretical Biology, 1974, 47(1): 209-221.

[4] WEIBULL J W. Evolutionary game theory[M].Cambridge:Massachusetts Institute of Technology Press, 1997.

[5] 郭本海, 方志耕, 劉卿. 基于演化博弈的區域高耗能產業退出機制研究[J].中國管理科學, 2012, 20(004): 79-85.

[6] 劉偉兵, 王先甲. 進化博弈中多代理人強化學習模型[J].系統工程理論與實踐, 2009 (3):28-33.

[7] 達慶利，張騏驥. 有限理性條件下進化博弈均衡的穩定性分析[J].系統工程理論方法應用, 2006 (6): 279-284.

[8] FOSTER D, YOUNG P. Stochastic evolutionary game dynamics [J].Theoretical Population Biology, 1990, 38(2): 219-232.

[9] 黃敏鎂. 基于演化博弈的供應鏈協同產品開發合作機制研究[J].中國管理科學,2010(12): 163-170.

[10] 邁克爾 波特.競爭戰略[M].陳小悅,譯. 北京：華夏出版社，1997.