基于橢球約束的徑向基函數隱式曲面重建

韓 燮， 武敬民， 韓慧妍， 李定主， 孫福盛

(1.中北大學計算機與控制工程學院，山西 太原 030051；2.中國兵工集團207所，山西 太原 030051)

Han Xie1, Wu Jingmin1, Han Huiyan1, Li Dingzhu2, Sun Fusheng1

(1.School of Computer and Control Engineering,North University of China,Taiyuan Shanxi 030051,China;2.207,China Ordnance Group,Taiyuan Shanxi 030051,China)

在計算機仿真中，對散亂數據點進行曲面擬合是一項基本任務。點云表面重建的常用方法有顯式重建和隱式重建兩種：顯式方式通常描述表面的位置，可表示為映射23S:R→R；隱式方式通常用標量函數的等值面來描述，可表示為映射3F:R→R，其中顯式曲面一般又可分為參數曲面和三角化表面。三角化方法是通過點云的Delaunay三角剖分[1-3]或者Voronoi圖來構造得到的拓撲關系，該方法的優點是空間和時間復雜度僅取決于擬合的點數，能夠得到高質量的三維網格曲面。三角化方法的缺點也很明顯，第一，點云數目增大時，網格化的效率會降低；第二，點云噪聲會對剖分后的效果造成嚴重的不保形；第三，對采樣密度很敏感等。參數曲面在繪制、細分等方面表現突出。隱式曲面的優勢有以下幾個方面：第一、很容易辨別點在曲面的內側或者外側，有利于解決碰撞檢測問題；第二、擬合時對點云中的噪聲點不敏感，表面法向量易計算；第三、可以用簡單的幾何體混合成表面復雜光滑的物體等。由于隱式曲面具有的優點，尤其是簡單的徑向基函數，使得隱式曲面在很多領域廣泛使用。

1982年Franke[4]第一次提出對散亂點云進行徑向基函數插值擬合，該方法穩定且精確，但因是全局支撐，對于大規模點云擬合時，效率低下且易變形。1995年Savchebko等[5]對Franke的方法加入了一次多項式約束，但效果并未有較大改善反而計算量加大。Carr等[6]先計算出表面法向量，依據法向量約束來完成曲面重建，但計算量大，且方向不易辨別。

本文綜合了徑向基函數理論和橢球理論[7-9]，利用帶有橢球約束的徑向基函數對點云進行擬合。擬合點云時直接對散亂點云進行擬合，不需要計算法向量等信息。不過本方法較適合擬合小規模來自封閉物體的點云，否則擬合后的模型會出現冗余部分，造成擬合結果不保特征且效率低下。此時需將點云進行適當分割并同時擬合分割的點云，然后對它們進行光滑混合[10-12]。

1 徑向基函數

Blinn[13]提出元球模型，該技術采用具有等勢場值的點集來定義曲面。元球模型被定義為be-ar2，其中r是從空間特定點到等勢場的距離。這種模型有很多變形,一般情況下，影響場可用關于距離r的函數Φ(r)。對于Blinn模型中的Φ(r)=e-ar2是高斯徑向基函數，其他的基函數主要有以下幾種：

(1)Φ(r)=r(線性函數)；

(2)Φ(r)=r3(三次函數)；

(3)Φ(r)=r2log(r) (薄板樣條)；

(4)Φ(r)=(1+r2)1/2(多二次函數)；

(5)Φ(r)=(1+r2)-1/2(逆多二次函數)。

通常徑向基函數隱式曲面的公式如下：

其中，P=(x,y,z)表示任意點，Pi表示采樣點，λi表示對應每一個徑向基函數的權重，是歐幾里得距離，是一正定基函數，Ρ(Ρ)是一個多項式。多項式Ρ(Ρ)可看作一種約束，根據經驗選擇多項式時一般不超過四次，因四次以上，很難控制其擬合結果，本文選擇二次橢球。

2 基于橢球約束的RBF隱式曲面擬合

2.1 RBF隱式曲面擬合

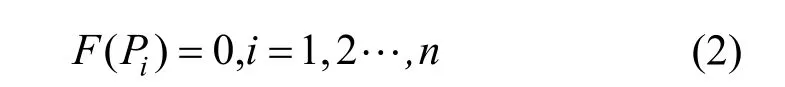
可將式(1)分解為兩部分，并將這兩部分映射到兩個空間上：

令V1代表基函數空間：

令V2代表多項式部分的空間：

式中Ρj代表多項式函數，為使能量函數最小需讓其滿足正交條件即：

在空間V1和V2中，分別假設

則式(1)可寫成下面的形式：

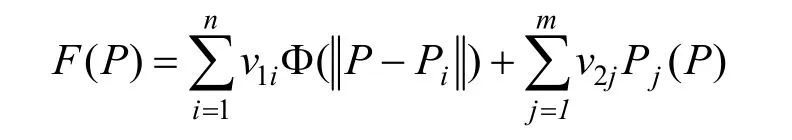
在隱式曲面上的點，均滿足F(Ρk)=0，對于k,k=1,2,…,n，有下式：

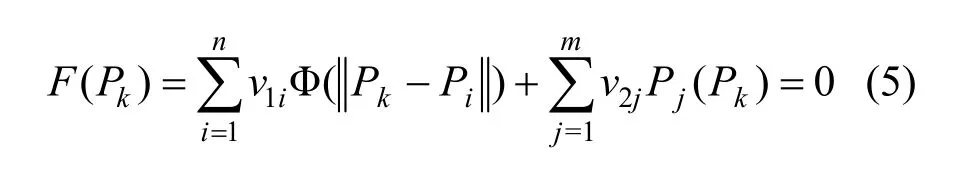
根據正交條件可將式(5)寫成矩陣的形式：

其中矩陣A=(aij)n×n且aij=Φ，矩陣B=(bij)m×n且bij=Ρj(Ρi)。

假設矩陣M和ξ分別為：

利用式(1)對點云擬合現在等價于下面的線性系統：

為避免平凡解的存在，需對ξ稍作限制。一般限制形式如下：

式中D是半正定矩陣。通常情況下，可能沒有ξ同時滿足式(1)和式(10)。所以，用式(11)更能有效地解決這種問題：

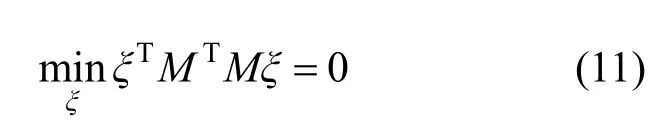
式(11)中的ξ必須滿足式(10)。

對于式(10)的解可以通過求特征值來解出：

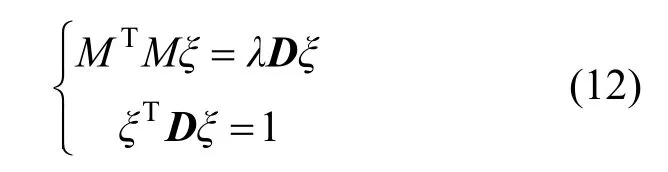
當D是一個單位矩陣時，隱式曲面的解是式(13)的特征值系統中最小特征值對應的單位特征向量0ξ。

2.2 帶有橢球約束的RBF隱式曲面擬合

通常拋物面的公式如式(14)所示：

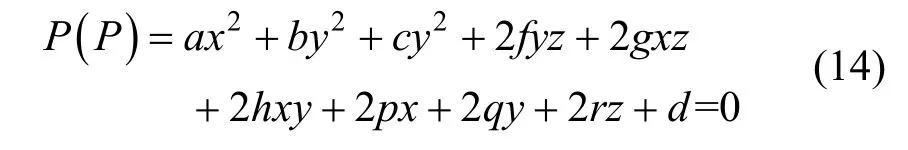
式中Ρ代表三維點數據。

令：

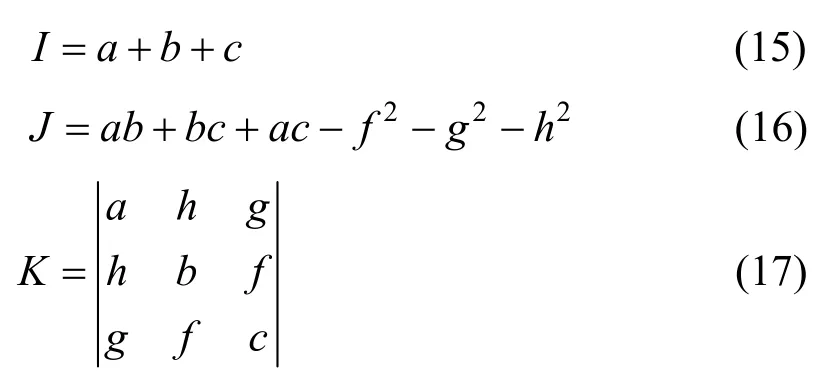
不管拋物面如何平移、旋轉，I、J、K的值是不變的，當且僅當J＞0且I、K＞0時，式(14)才表示為橢球。

使用J＞0且I、K＞0來保證式(14)為橢球時，會反復利用非線性約束來進行迭代優化等，使得計算復雜、效率低，需選用一種簡單而直接的方法。文獻[14]指出只需滿足式(18)即可達到式(14)為橢球的目的。

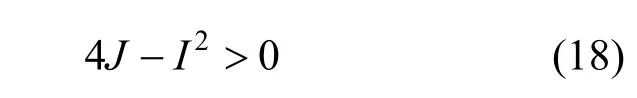
對于式(18)從幾何意義來說，它表示短軸的長度至少要大于等于長軸的一半，即24J-I必須是大于零的數。

對式(14)進行調整：

由此可以得出式(6)中代表多項式部分的空間v2。

對應過點Ρi(xi,yi,zi),i=1,2,…n的式(6)中對應的矩陣B為：

式中

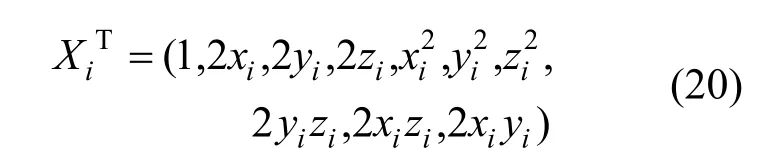
求帶橢球約束的隱式曲面方程實際上又變成求在24J-I＞0條件下的線性系統，如下式：

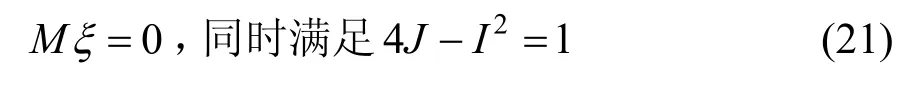
通過式(15)、(16)和(21)中的24J-I=1可以求出一個矩陣C0：

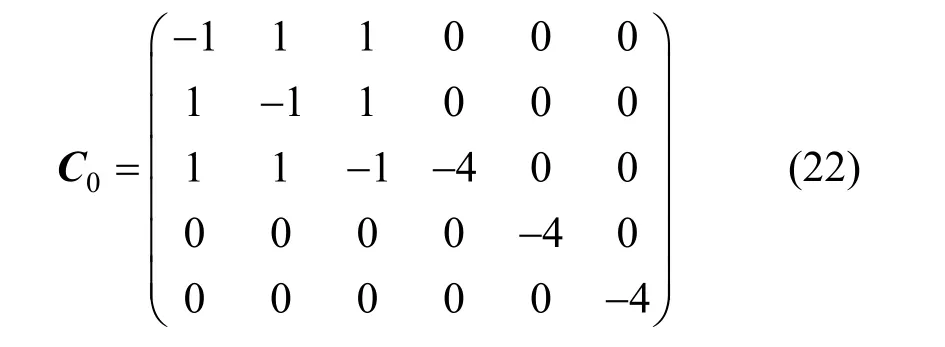
使得：

再定義一個矩陣C：

條件4J-I2=1可以轉化為：

式中的O11,O12,O21分別為(n-6)×(n-6),(n-6)×6,6×(n-6)大小的零矩陣。現將式(7)、(8)式的矩陣重新分塊：

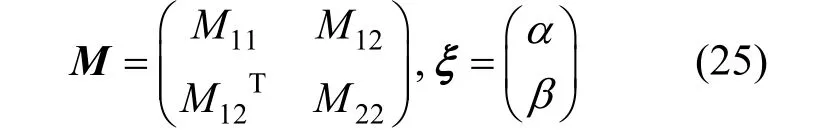
式中，M11,M12,M21分別是大小為(n-6)×(n-6),(n-6)×6,6×(n-6)，α,β的大小分別為(n-6)×1和6×1，式(21)現可簡化為：

當M11是非奇異時，式(26)的求解等價于求解下式中的β：

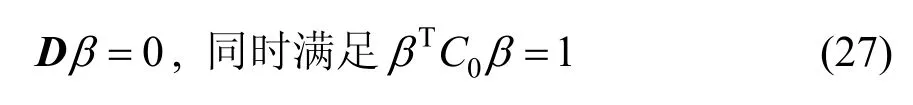
式中D=M22-MT12M11-1M12=-M12TMM11MM12,因M22是零矩陣，可以直接求出β，α。但當D是非奇異矩陣時，式(27)無解，此時通常會選用最小化方法來求解。首先矩陣D是對稱的、正定的，利用下式求解：

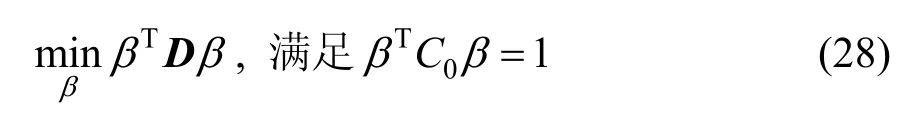
帶橢球約束徑向基函數方程的求解變換為常見的特征值系統問題：

對一般的徑向基函數，矩陣D不一定必須為正定的。不是正定時，需用至少是半正定的TDD來代替D，方程的解是最小非負特征值對應的特征向量，但解不能保證唯一。

3 隱式曲面光滑拼接

本文選用文獻[10]提出的可自行控制參數的光滑絕對函數來對分塊后的重構模型進行光滑拼接。

定義1.表示當x大于等于0時=x，當x小于0時=-x，引進如下絕對值函數：

對于光滑拼接我們只需保證光滑函數達到平方次光滑即可。式(30)的一階和二階光滑函數的顯式形式為：

式(30)可轉化為另一種等價形式：

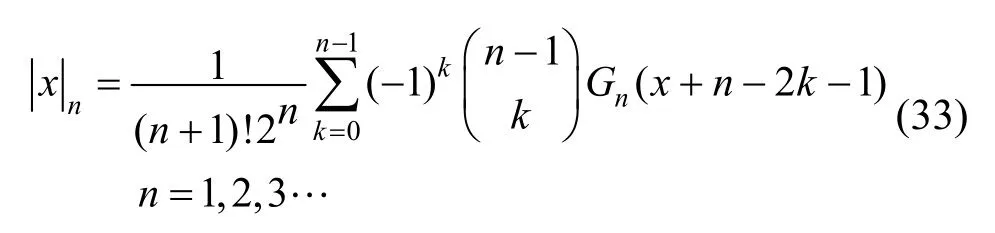
式中的Gn(x)為：

依據式(33)可以計算出和：

定義2.對于δ＞0并且n＞0，我們定義：

簡明地說就是，當＞δ時,δ=,事實上，當≥δ時有≥n。故：

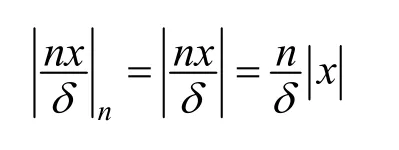
由此可得出光滑拼接的函數為：

由以上定義得出由n,δ共同控制的光滑函數，要根據具體需要來選擇參數的值。一般情況選擇n=2,因為二次光滑效率高且光滑效果不錯。對于δ，對兩個半徑大小為0.5的圓球進行實驗，根據效果來確定，如圖1所示。

4 實驗與分析

為驗證本算法的效果和效率，與文獻[1-2]、[4-5]進行了對比實驗。硬件實驗環境為：AMD X4 740，4 G內存，軟件環境為Windows8 64位操作系統、VS2008 C++、OpenGL,Matlab2013等。

下面將對femur、head兩種點云進行五種方法的重建工作，并對其重建效果進行分析，詳見圖2、3中的(b)、(c)、(d)、(e)、(f)分別對應文獻[1-2]、[4-5]和本文方法的效果圖。

圖2和表1表明各種算法對femur點云的重建效果，算法[1]、[4]、[5]三種在效果上、效率上都沒有優勢，算法[2]雖能大體上保特征，但效率卻遠低于本算法。

圖1 光滑函數操作

圖3和表1表明各種算法對head點云的重建效果，算法[1]、[4]、[5]明顯不保特征，算法[2]基本保特征，但五官信息、喉結特征沒有保留，本算法雖然出現腫脹部分，但細節特征依然保留。

圖2 femur點云擬合

總體來說，算法[1]是對點云進行三角剖分，重建模型外表比較粗糙。算法[2]對點云進行Loop細分重建，重建模型表面雖然光滑了很多，但卻丟失了細節特征。算法[4]利用基于徑向基函數隱式曲面重建，該方法雖然重建模型表面光滑連續，但模型不飽和，有失真現象。算法[5]利用平面約束的徑向基函數隱式曲面重建，相對于算法[4]而言，重建模型稍有飽和，較精確地重建出模型，但有一個明顯的平面，使得整個模型重建效果不好。

對于本文提出的橢球約束徑向基函數隱式曲面重建方法。可以看做先對點云進行基于徑向基函數方法重建，然后對整個模型曲面進行橢球曲面約束。相當于一個徑向基函數隱式曲面和一個橢球隱式曲面的線性光滑混合。利用橢球的幾何特性對徑向基函數隱式曲面進行飽和處理，從而使得整個模型飽和精確。

實驗表明基于橢球約束的徑向基函數方法重建后的模型比較精確，且圓潤飽和。但對于有尖銳特征的點云重建時(如head)，因為橢球的作用會形

表1 實驗數據對比

圖3 head點云擬合

成腫脹部分。對于此缺陷，需對點云進行簡單重疊分割。首先觀察head點云，在耳朵處(y=1.5)出現腫脹，需在此進行線性分割，分割為上下兩部分。這兩部分需要有重疊，以便拼接處理，所以將y=1.0以上部分分割為上半部分，將y=2.0以下部分分割為下部分。如圖4所示，圖中(a)表示上半部分，(b)表示下半部分。如圖5所示，將帶有尖銳特征點的云分割后，會使得尖銳特征性變小，然會對分割后的局部點云重建并進行橢球約束，從而在不出現腫脹現象的情況下，局部點云生成的模型更具有飽和性，保特征性。最后通過對局部模型進行光滑拼接。共消耗時間4.25 s，效率明顯提高。

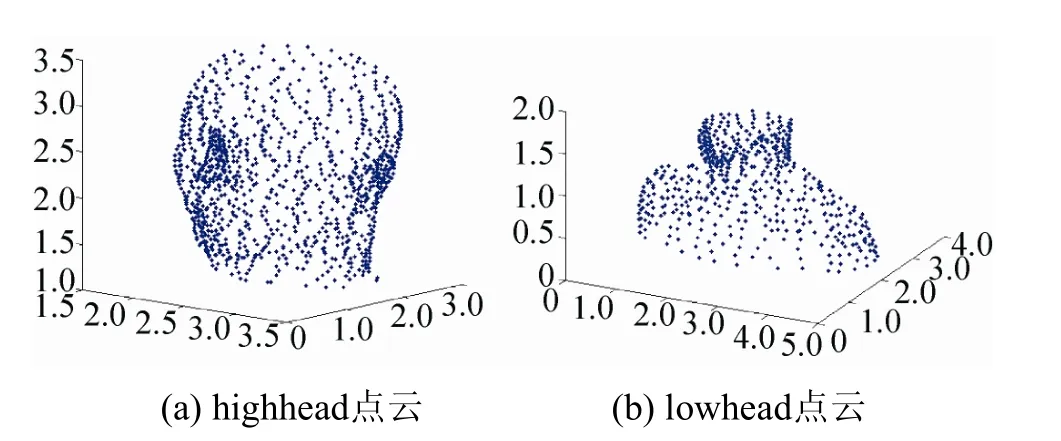
圖4 head點云分割示意圖

圖5 光滑拼接效果

5 結 論

本文提出的基于橢球約束的徑向基函數隱式曲面重建算法，直接從散亂點獲取重建信息，重建結果精確。但對大規模點云集擬合時，需解大規模矩陣，效率低下甚至擬合模型會產生冗余部分。要通過對點云進行簡單的分割再進行擬合光滑拼接，不僅效果好而且是并行擬合，這樣時間效率會飛速提高。實驗效果表明：本算法相對于上面提到的效果保特征性好而且效率很高。

[1]Kuo C C,Yau H T.A Delaunay-based region-growing approach to surface reconstruction from unorganized points [J].Computer-Aided Design,2005,37(8):825-835.

[2]Cheng Fuhua,Fan Fengtao,Lai Shuhua,Huang Conglin,Wang Jiaxi,Yong Junhai.Loop subdivision surface based progressive interpolation [J].Journal of Computer Science and Technology,2009,24(1): 39-46.

[3]陳慧群,黎景炎.基于變形網格法的高密點云曲面重建[J].工程圖學學報,2011,32(2): 64-67.

[4]Franke R.Scattered data interpolation: Tests of some methods [J].Mathematics of computation,1982,38(157):181-200.

[5]Savchenko V V,Alexander A P,Okunev OG,Kunii T L.Function representation of solids reconstructed from scattered surface points and contours [J].Computer Graphics Forum,1995,14(2): 181-188.

[6]Carr J C,Beatson R K,Cherrie J B,Mitchell T J,Fright W R,McCallum B C,Evans T R.Reconstruction and represe-ntation of 3D objects with radial basis functions [C]//Proceedings of the 28th annual conference on Computer graphics and interactive techniques.ACM,2001: 67-76.

[7]Klein P P.On the Ellipsoid and Plane Intersection Equation [J].Applied Mathematics,2012,3(11):1634-1640.

[8]Beck A,Sabach S.An improved ellipsoid method for solving convex differentiable optimization problems [J].Operations Research Letters,2012,40(6): 541-545.

[9]Reiner T,Mückl G,Dachsbacher C.Interactive modeling of implicit surfaces using a direct visualization approach with signed distance functions [J].Computers & Graphics,2011,35(3): 596-603.

[10]Li Qingde.Smooth piecewise polynomial blending operations for implicit shapes [C]// Computer Graphics Forum,2007,26(2): 157-171.

[11]Li Qingde,Tian Jie.Partial shape-preserving splines [J].Computer-Aided Design,2011,43(4): 394-409.

[12]李凌豐,譚建榮,趙海霞.Metaball 重疊區域作用效果混合[J].中國圖象圖形學報,2006,11(5): 695-699.

[13]Blinn J F.A generalization of algebraic surface drawing [J].ACM Transactions on Graphics (TOG),1982,1(3):235-256.

[14]Li Qingde.Registration techniques for computer assisted surgery [D].UK: University of Hull,2001.