基于二項式系數設計矩陣的Bézier曲線擴展

郭大勇， 成佳頤

(清華大學機械工程系，北京 100084)

在計算機輔助幾何設計(computer aided geometric design,CAGD)和計算機圖形學(computer graphics,CG)領域中，常利用參數化的曲線曲面來進行交互式設計。當在表示曲線或曲面的時候，如果想要保持曲線曲面的形狀，很重要的一點就是基函數的選取。因此，以Bernstein多項式作為基函數的Bézier曲線曲面模型有著廣泛的應用[1]。但是該模型的不足之處在于，若需要根據需求調整Bézier曲線曲面的形狀，就必須對原始控制點進行調整，這不便于實際使用。為了改善這種情況，一種可行的方法就是對Bernstein基函數添加形狀參數，使得在原始控制點不變的情況下，實現對Bézier曲線曲面的調整。

近些年來，這種Bézier曲線的擴展方法大致分成三類[2]，分別為利用三角多項式思想;利用代數雙曲思想和利用多項式思想。其中，利用多項式思想的Bézier曲線擴展的研究成果如下：文獻[3-6]分別給出了Bézier曲線的二次，三次，四次和五次含參擴展。文獻[7-10]給出了Bézier曲線的n次含參擴展，其中文獻[7-9]直接給對應的基函數表達式，而在文獻[10]中，作者利用de Casteljau算法將4次含參Bernstein基函數遞推到了n次。

本文根據二項式((1-t)+t)n-1的展開系數，引入含參的正系數矩陣Ann，在此基礎上推導出了同階含參的A-Bernstein基函數表達式，該表達式與Bernstein基函數具有類似的性質，對應A-Bézier曲線不僅有Bézier曲線的特性，而且可以通過改變參數來實現對曲線的調整。另外，通過對正系數矩陣Ann進行調節，亦可以實現對A-Bézier曲線的調整，使曲線的調控更加靈活。

1 正系數矩陣的推導及幾何解釋

定義1.當aij≥0(i,j=1,2,…,n)時

為所需的正系數方陣。

定義2.當t∈[0,1]，i=1,2,…,n時，稱關于t的多項式：

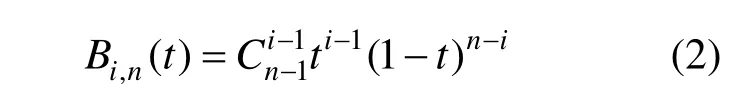
為n–1次Bernstein基函數，恰好對應二項式1((1-t)+t)n-1的展開項。其作為n–1次Bézier曲線的基函數，具有諸多優良性質，如正性、權性和對稱性等。

定義3.對于[]0,1t∈，Bézier曲線的控制多邊形頂點為p1,p2,…pn，則對應的Bézier曲線方程的矩陣形式為：

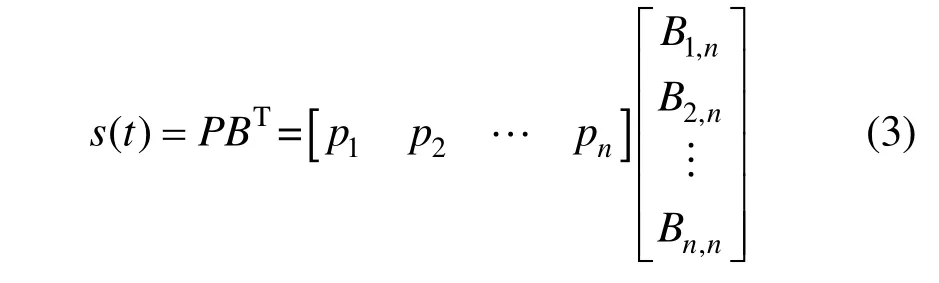
利用正系數矩陣Ann對Bernstein基函數矩陣進行調配，可得A-Bernstein基函數Tnn=AB。為了使滿足權性=1和對稱性可令Ann具有以下性質：

性質1.

性質2.

因此，A-Bernstein基函數對應的A-Bézier曲線為

對應的控制點矩陣：

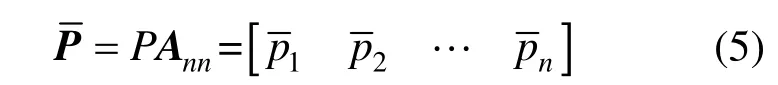
其中，=p1a1m+p2a2m+…+pnanm,m=1,2,…,n

新的控制點為原始控制點的加權平均，為了減少計算量，限定新的控制點為兩點加權平均，并分情況給出表達式：

(1) 當2,2,3,n=mm=…時

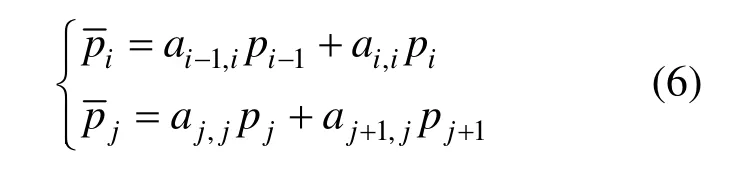
其中i=2,3,…,m，j=m+1,m+2,…,n-1

(2) 21,2,3,nmm=+=…時

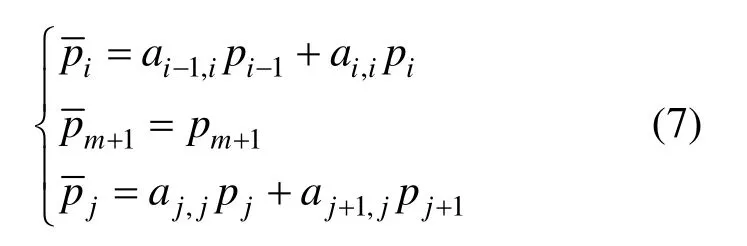
其中i=2,3,…,m，j=m+2,m+3,…,n-1

若已知，根據性質2，可得pj。且根據性質1可知=ai-1,ipi-1+ai,ipi，其代表的幾何意義為：點按比例分線段如圖1所示。

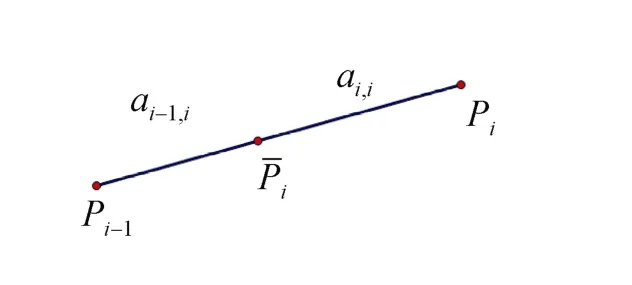
圖1 線段的定比分點

向式(1)中引入參數λ，通過改變λ的值來實現對新控制多邊形的調整，從而實現對A-Bézier曲線的調整。由于式(2) 依次對應了二項式((1-t)+t)n-1的展開項，為了減少計算量和簡化表達式，令式(1)中元素的分母與((1-t)+t)n-1的展開項系數相同，可得aij的分母為且規定當時，aij=1。對于式(1)的同一列上的兩個元素aij的分子，本文做如下分析：

為了保證擴展后的含參數λ的A-Bernstein基函數(t)在t∈[0,1]上隨著t的變化保持單調遞減，并且在0處取得最大值1，在1處取得最小值0。限定(t)=(1-λt)(1-t)n-2，因此可得式(1)的第一行：

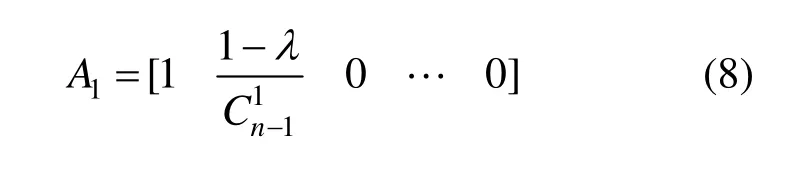
根據性質2可得Ann的最后一行：

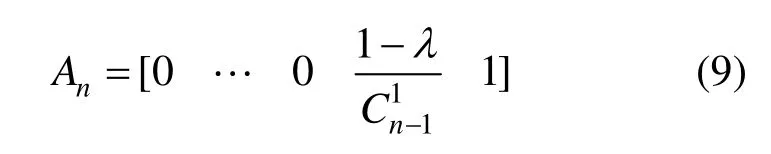
對于正系數矩陣(1)的同一列上的兩個元素aij的分子，取其中一個為(1-)λ，另一個可根據性質1求得，因此可得：

(1) 當n=2m,m=2,3,…時

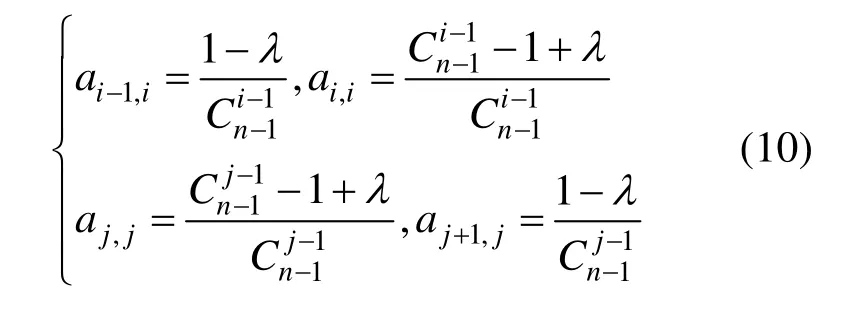
其中i=2,3,…,m，j=m+1,m+2,…,n-1

(2) 當n=2m+1,m=2,3,…時

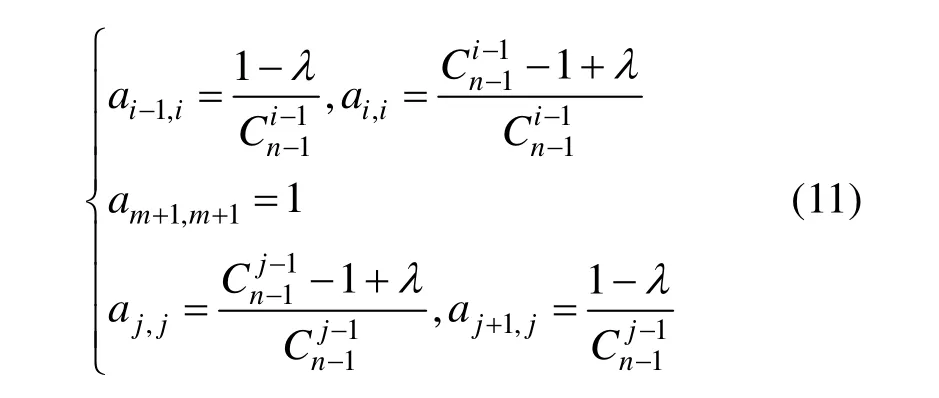
其中，i=2,3,…,m，j=m+2,m+3,…,n-1且當n=3時，a2,2=λ

由于Bézier曲線通過控制多邊形的起點p1與終點pn，所以令=p1，=pn，于是可知：

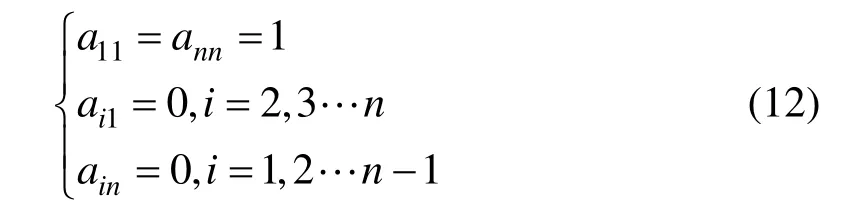
因此由式(8)~(12)可得正系數矩陣：

(1) 當n=2m,m=2,3,…時

(2) 當n=2m+1,m=2,3,…時

因為矩陣中所有元素為正，所以1-≤λ≤1。

以n=6為例，A-Bézier曲線為：

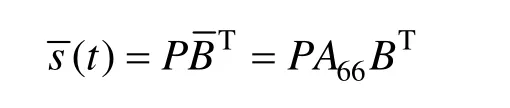
其所對應的新控制點為：

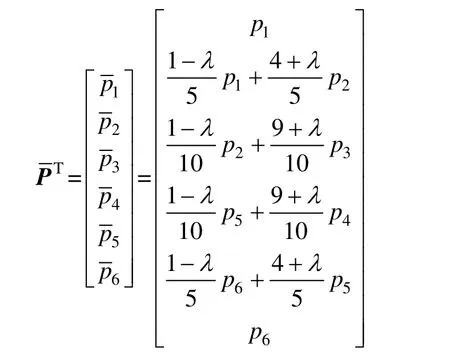
其控制多邊形如圖2所示：

其中虛線為新的控制多邊形，通過改變參數的取值可以實現對控制多邊形的調整，由于新控制點始終都是原始控制點的二點加權，所以保證了新曲線的凸包性。

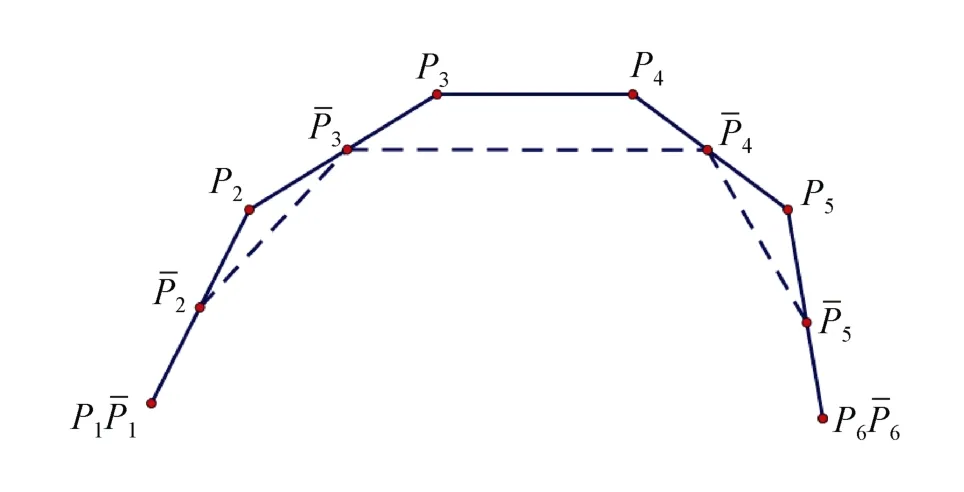
圖2 控制多邊形

2 同階含參A-Bernstein基函數表達式及性質

利用上述正系數矩陣可得擴展后的A-Bernstein基函數表達式：

(1) 當n=2m,m=2,3,…且1-≤λ≤1時

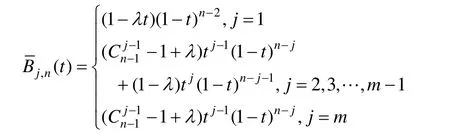
其中j=m+1,m+2,…,n時(t)=

(2) 當n=2m+1,m=2,3,…時，1-≤λ≤1時

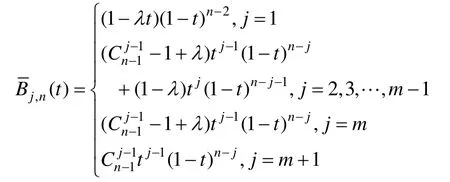
其中j=m+2,m+3,…,n時，(t)=+1-j,n(1-t)

下面給出A-Bernstein基函數的性質：

性質1.正性

(t)=ABT(t)，因為B(t)≥0,t∈[0,1]且Annnn為正系數矩陣，所以(t)≥0,t∈[0,1]。

性質2.權性

(t)=ABT(t)，因為nn且,m=1,2,…,n，所以1,t∈[0,1]。

性質3.對稱性

(t)=ABT(t)，因為B(t)=B(1-t)且nni,nn-i+1,n aij=an+1-i,n+1-j,1≤i,j≤n，所以(t)=

性質4.退化性

當λ=1時，Ann退化為單位矩陣，因為所以A-Bernstein基函數退化為Bernstein基函數。

對應的A-Bézier曲線具有如下性質：

性質1.端點特性

(1) 端點位置矢量：擴展后的曲線表達式為

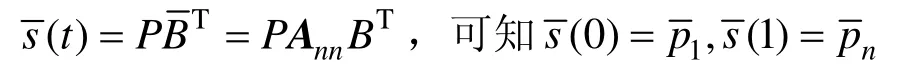
(2) 端點切矢量：擴展后的新控制多邊形頂點矩陣為：

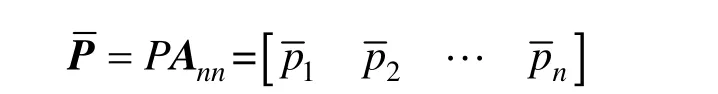
所以：

因此表明擴展后的曲線與首末兩邊矢相切，模長關系確定。

性質2.對稱性

若保持控制多邊形頂點的位置不變，只是把順序顛倒，那么新Bézier曲線與原曲線重合。

性質3.凸包性

因為(t)=1,t∈[0,1]且(t)≥0,t∈[0,1]，所以有：

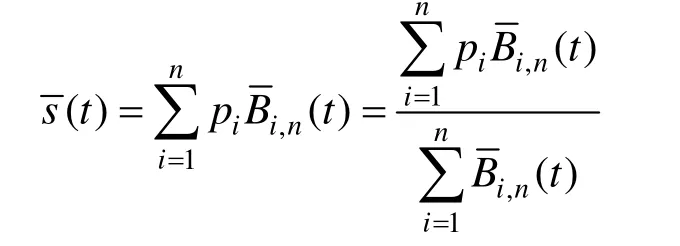
此式與重心的位置公式相同，分母可代表一個總質量為1的質點系，而該系統中各質點的位置矢量就為pi，質點的質量按照(t)分布，所以(t)為重心的位置。當t在[0,1]間變化時，各質點的質量也在隨(t)變化，所以變化的(t)的軌跡就為對應的Bézier曲線，因此，s(t)上各點必然在pi的凸包內。

性質4.幾何不變性

由于Bézier曲線具有幾何不變性，Ann為正系數矩陣且具有性質1和性質2，這使得調配后的Bézier仍有幾何不變性。

性質5.退化性

當λ=1時，A-Bézier曲線將退化成Bézier曲線。

3 n=6時的A-Bernstein基函數和A-Bézier曲線

當n=6，t∈[0,1]，λ∈[-4,1]時，對應的正系數矩陣Ann，A-Bernstein基函數和圖像，及對應的A-Bézier曲線圖像：

圖3左側為5次A-Bézier曲線，從上到下對應λ=1,0,-1,-2,-3,-4，當λ=1時退化為標準Bézier曲線；右側為λ=1,0,-1,-2,-3,-4時的A-Bernstein基函數曲線。

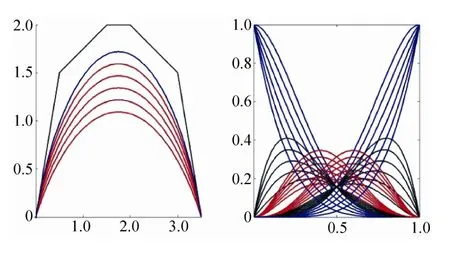
圖3 5次A-Bézier曲線與A-Bernstein基函數曲線

4 正系數矩陣的調整性

4.1 添加參數

通過改變λ的范圍，可以在某方向上調整A-Bézier曲線。在保持Ann的性質1,2的基礎上，通過添加參數的方法，可令A-Bézier曲線在多個方向上進行調整。以n=6為例，向Ann添加參數β，可得：

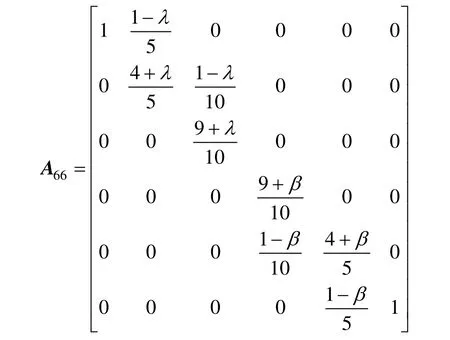
當t∈[0,1]，λ,β∈[-4,1]時，對應的A-Bernstein基函數為：

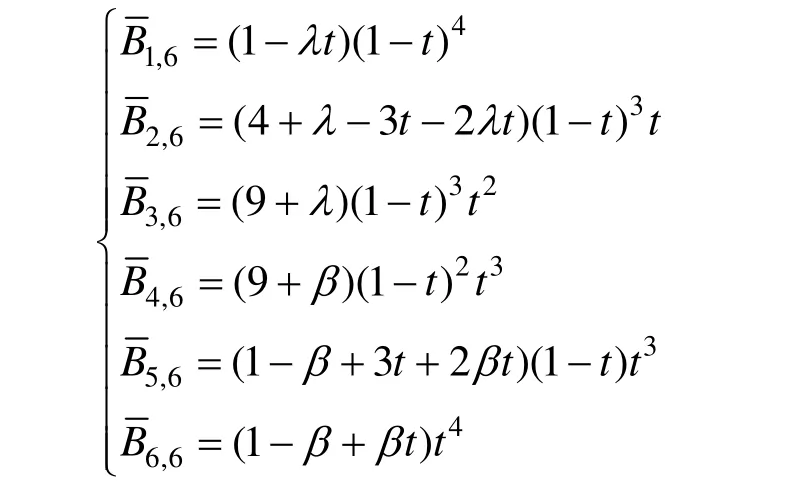
可以通過對兩個參數λ,β取不同的值實現曲線在多個方向上的調整，圖4中虛線對應的參數分別為λ=1,β=-4和λ=-4,β=1，實現在了不同方向上的調整。

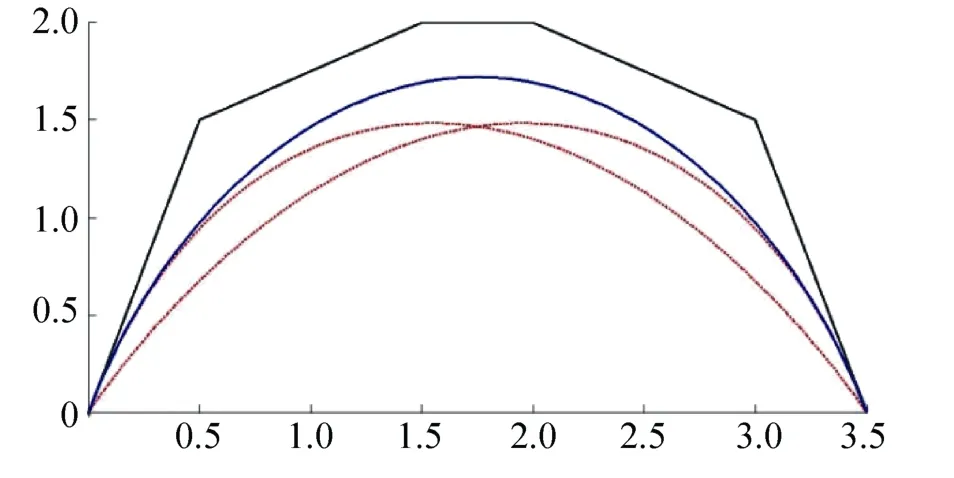
圖4 曲線的含參調整

4.2 矩陣列移位

在保證Ann的性質1和性質2的基礎上，通過對Ann的列元素進行移動，可實現對曲線“胖瘦”的調整。以n=6為例，令第三列元素循環下移一個單位，令第四列元素循環上移一個單位，可得：

當t∈[0,1]，λ∈[-5,1]時，對應的A-Bernstein基函數為：

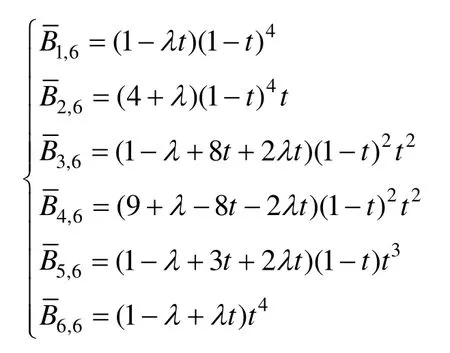
如圖5所示，上下為變化前后的A-Bézier曲線和A-Bernstein基函數曲線，由于移動了Ann的列元素，使得矩陣元素更加集中，從而導致了A-Bernstein基函數的更加緊湊，所以使得對應的A-Bézier曲線更加“瘦”，圖6中為調整前后的Bézier曲線。

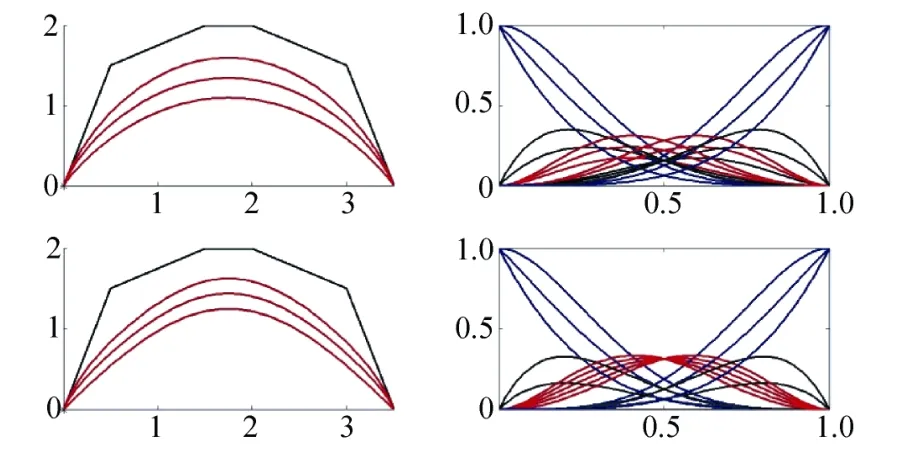
圖5 矩陣元素調整前后的曲線

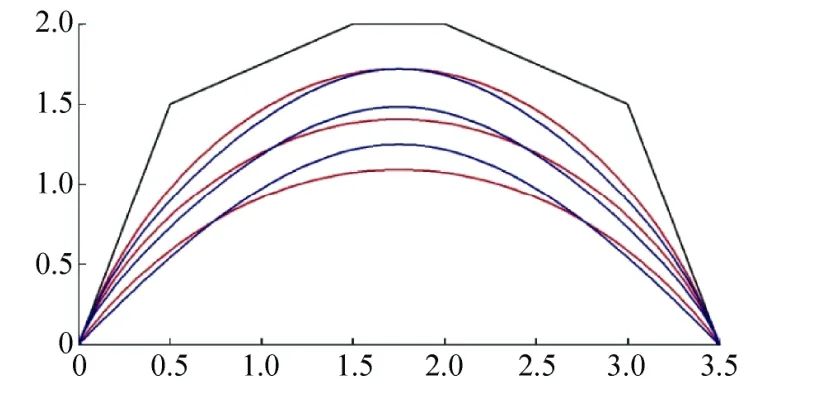
圖6 矩陣元素調整后的曲線

5 應用實例

利用5次A-Bézier曲線繪制花瓣圖形，圖7為含單參的A-Bézier曲線，其中λ=-4,-3,-2,-1,0,1。圖8為含雙參的A-Bézier曲線，其中λ=-4,-3,-2,-1,0,1，β=1,0,-1,-2,-3,-4。圖9為利用正系數矩陣的列元素位移使得A-Bézier曲線變“瘦”的實例。

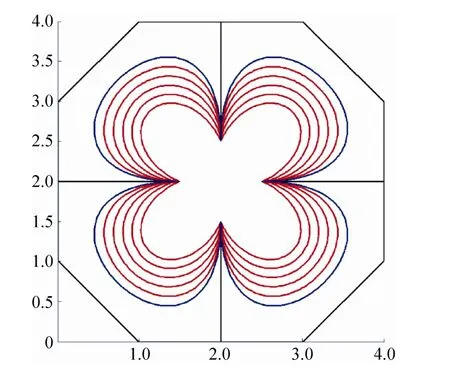
圖7 含單參的A-Bézier曲線

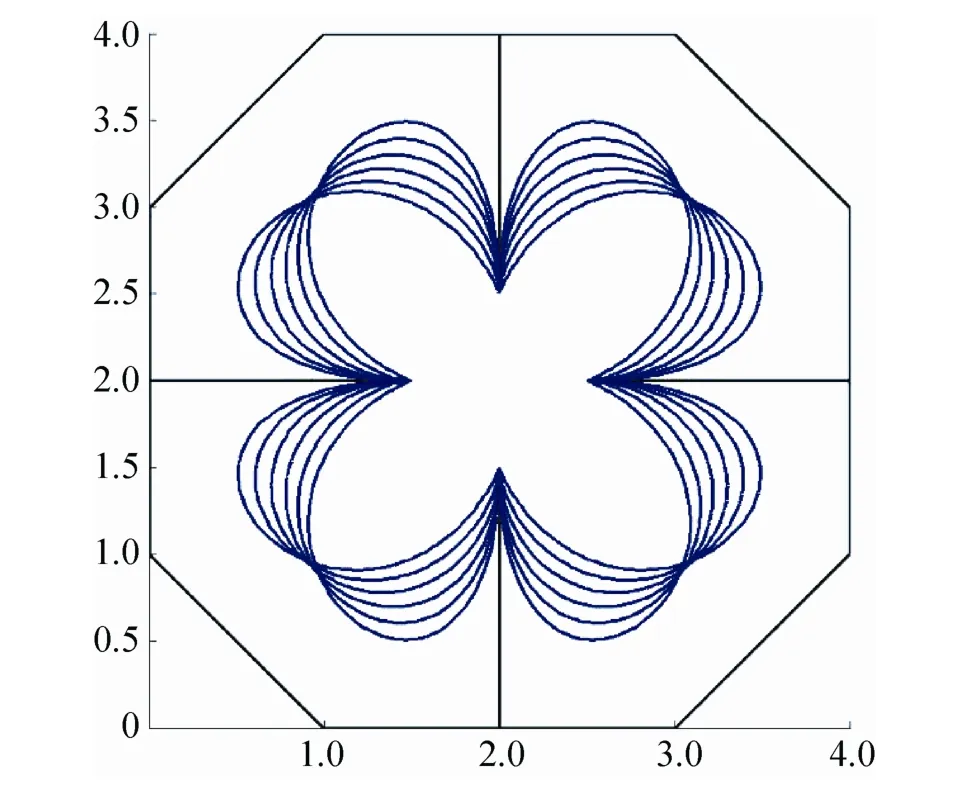
圖8 含雙參的A-Bézier曲線

6 結 論

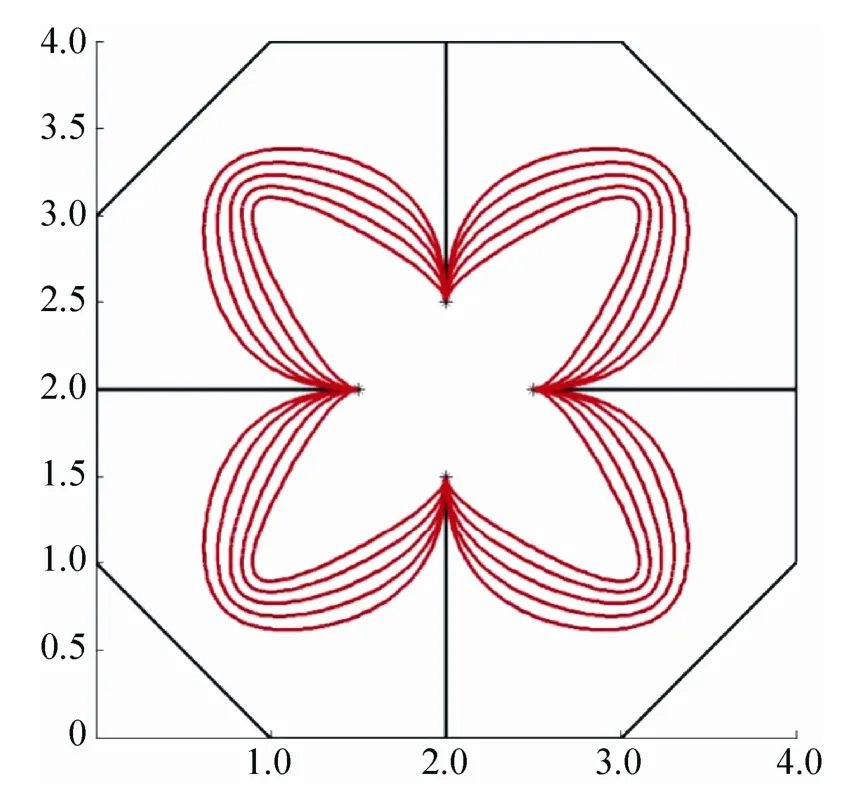
圖9 矩陣元素位移后的曲線

以Bernstein多項式作為基函數的Bézier曲線曲面，憑借著其許多良好的幾何性質，在CAGD，CG領域有著廣泛的應用。論文以二項式的展開系數為基礎，通過含參的正系數矩陣對Bernstein基函數進行調配，得到了同階含參的A-Bernstein基函數，以及對應的A-Bézier曲線。證明了A-Bernstein基函數和A-Bézier曲線分別具有Bernstein基函數和Bézier曲線類似的性質，并且A-Bézier曲線的形狀在原始控制點不變的情況下，不但可以通過形狀參數進行調整，還可以通過修改正系數矩陣進行調整。最后通過舉例說明了方法可行有效，在幾何造型中方便于交互設計。

[1]施法中.計算機輔助幾何設計與非均勻有理B樣條[M].北京: 高等教育出版社,2001: 114-163.

[2]鄒 靜.Bézier曲線的擴展研究[D].杭州: 杭州師范大學,2012.

[3]韓旭里,劉圣軍.二次Bézier曲線的擴展[J].中南工業大學學報 (自然科學版),2003,34(2): 214-217.

[4]秦新強,胡鋼,張素霞.三次Bézier曲線的新擴展及其應用[J].計算機工程與應用,2008,44(2):112-115.

[5]劉小瓊,楊國英.帶兩個形狀參數的四次Bézier曲線的擴展[J].圖學學報,2013,34(1): 41-45.

[6]翟芳芳.帶兩個形狀參數的五次Bézier曲線的擴展[J].大學數學,2012,28(3): 59-63.

[7]劉 植,陳曉彥,張 莉,時 軍.Bézier曲線曲面的同次擴展[J].中國科技論文在線,2011,6(10): 721-725.

[8]劉 植.Bézier曲線的擴展[J].合肥工業大學學報(自然科學版),2004,(8): 976-979.

[9]程黃和,曾曉明.帶形狀參數的Bézier曲線[J].廈門大學學報(自然科學版),2006,45(3): 320-322.

[10]嚴蘭蘭,宋來忠.帶兩個形狀參數的Bézier曲線[J].工程圖學學報,2008,29(3): 88-92.