基于積分協方差矩陣的粒子濾波目標跟蹤
顧 鑫,王 華,李 喆,李志國,王 倩,鄧志均
(中國運載火箭技術研究院研究發展中心,北京100076)
1 引言
目標跟蹤在眾多領域都有應用,如視頻監控、運動目標捕捉、飛行器自主導航等[1]。在實際應用中,目標跟蹤會面臨著各種環境的干擾,跟蹤的魯棒性會受到影響[2]。
目標跟蹤的一個核心是選擇表征目標的特征,常用跟蹤算法僅選取顏色、光流等單一特征表征目標,由于跟蹤系統的復雜性,單一特征跟蹤魯棒性較低[2]。本文采用一種可融合目標灰度、梯度和空間位置分布的協方差矩陣來表征目標,該特征不含特征點數量和順序信息,對目標旋轉、尺度變化及光線變化都具有較強適應性[3]。跟蹤在實際應用中的另一個重要問題是計算的實時性,為了提高計算效率,本文在粒子濾波的框架下引入積分圖的概念,用協方差矩陣表征目標,實現對目標的跟蹤。
2 協方差區域描述子
協方差區域描述子的表征如圖1所示,令I為圖像幀,從I中提取一個大小為W×H×d維的特征圖像:

其中,Φ表示任意一種映射,N=W×H,區域R用d×d維的協方差矩陣表示[4]:
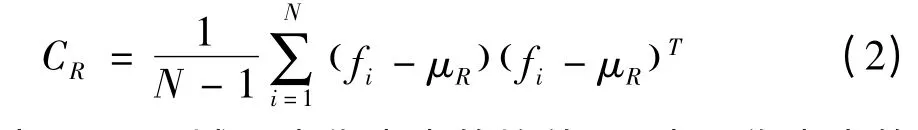
其中μR是區域R內像素點的均值;N表示像素點的數目。
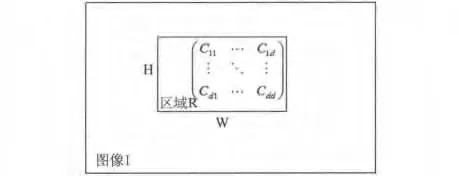
圖1 協方差矩陣表征目標區域示意圖
3 基于協方差區域描述子的目標跟蹤
3.1 積分協方差矩陣計算
粒子濾波算法中的每個粒子用協方差矩陣來表征,計算復雜度太高,難以實現實時運算,為了實現快速計算,引入積分圖的概念[5],將式(2)中的均值μ代入展開得:
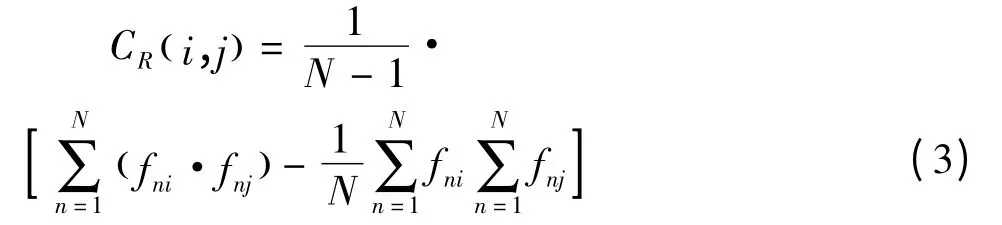
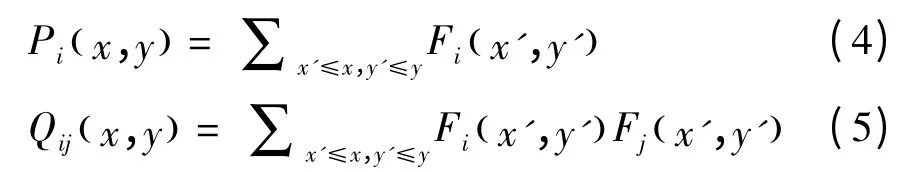
定義向量Px,y和矩陣Qx,y:
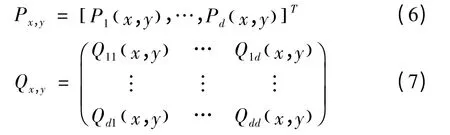
通 過 積 分 圖 計 算 Px,y和 Qx,y,則 區 域的表征因子計算如下:
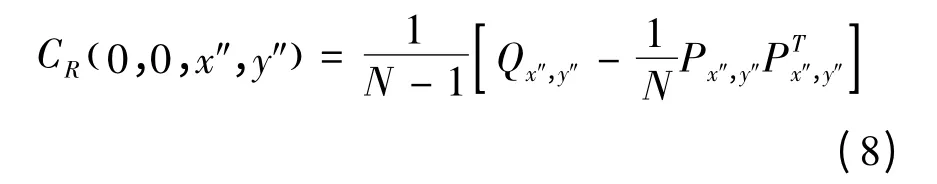
其中,N= ( x″+1 )× ( y″+1 ),經過一系列的變換可以得到區域R( x',y',x″,y″)內的協方差區域描述因子為:
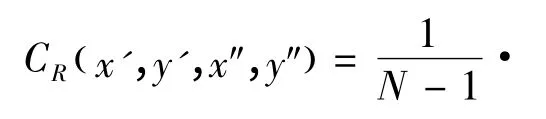
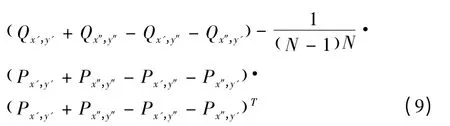
3.2 協方差矩陣之間的度量
兩協方差矩陣的相似度用兩者之間的距離來度量[6]:
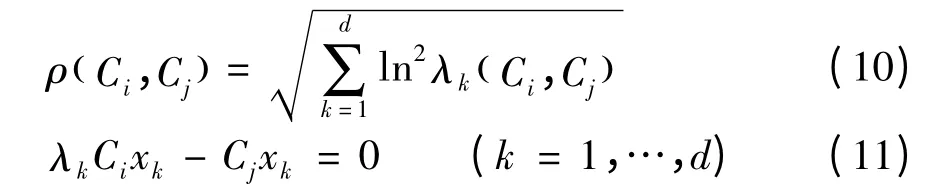
其中,xk為廣義特征向量;λk( Ci,Cj)是廣義特征值,每個粒子的觀測概率定義為:
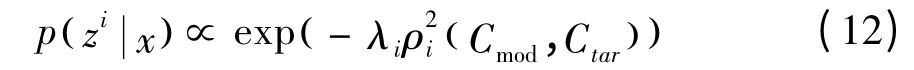
式中,Cmod和Ctar分別為目標模板和每個觀測粒子的協方差矩陣。
3.3 算法流程
本文算法實現流程如下:
(1)根據目標初始狀態x0,計算協方差矩陣模板C0,令
(2)預測:由xt=Axt-1+W,預測下一幀狀態^xt;
(3)在目標狀態xt-1周圍一定區域內計算每個粒子的協方差矩陣及其觀測概率;
(5)計算目標的當前估計狀態:珋xt=
(7)轉向步驟(2)。
4 仿真試驗結果
用目標區域內的每個像素點位置、灰度、一階導數和二階導數等9維特征向量得出一個9×9協方差矩陣。為了驗證算法的普適性,在數據源的選取上,選擇在公共視頻集上進行驗證,該視頻集共773幀,圖像的大小為640×480。在同一數據源上,針對同一目標,在人工標定初始位置的前提下,分別進行顏色跟蹤、邊緣跟蹤和本文算法跟蹤的仿真。如圖2所示,第一行是選擇顏色作為目標區域描述子的實驗結果,第二行為選擇邊緣作為目標區域描述子的實驗結果,第三行為本文算法跟蹤的結果。在第725幀,由于跟蹤目標進入陰影區,光線發生較大變化,導致目標的顏色特征發生較大變化,顏色跟蹤失效,本文算法和邊緣跟蹤可以一直跟蹤目標。在第758幀,目標受到部分樹木的遮擋,背景周圍存在較大邊緣特征的干擾,導致了邊緣跟蹤跟丟目標,協方差描述子中除了梯度特征外,還有灰度特征,因此本文算法可以穩定跟蹤目標。

圖2 試驗結果
表1是三種實驗結果的對比,由于相似目標、背景邊緣等外界因素干擾,單個特征(如顏色、邊緣)的跟蹤結果往往是不穩定的,通常情況下難以確定哪種特征的跟蹤效果更好。協方差矩陣包含目標區域每個像素點的位置信息,當特征的分布產生平移,對協方差矩陣的影響較小,因此該特征對光線變化不敏感。協方差矩陣中除了有目標區域每個像素點的梯度外,還包含了目標的灰度特征,因此對邊緣干擾有一定的糾錯能力。
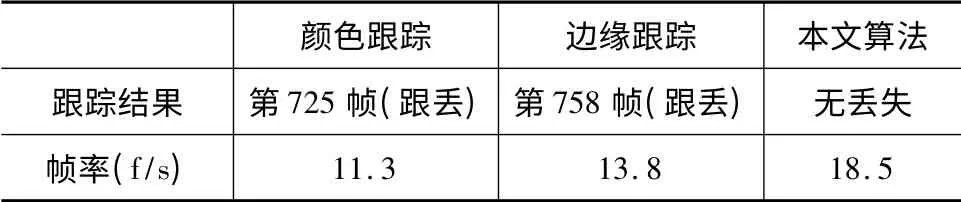
表1 試驗結果對比
本文中的所有算法均在Intel(R)Core(TM)i7 2.93 GHz 4G內存計算機上用Matlab R2010a仿真實現。本文的三種算法粒子數目均為100,采樣點數均為120,表1給出了不同算法的跟蹤速度(幀/秒),由表1可知,本文算法的復雜度比顏色跟蹤及邊緣跟蹤的算法復雜度都低,計算效率更高。
5 結論
本文提出了一種基于積分協方差矩陣的粒子濾波目標跟蹤,協方差矩陣可融合目標區域的不同特征實現復雜背景下目標的穩定跟蹤,利用積分圖實現區域協方差快速計算。試驗證明本文的跟蹤結果較單一特征跟蹤結果更穩定,算法的計算復雜度低,計算實時性更好。本文的跟蹤算法除了可以在公共安全、視頻監控等領域應用外,還可用于視覺導航、視覺導航、自主定位等方面。
[1] HOU Zhiqiang,HAN Chongzhao.A survey of visual tracking[J].Acta Automatica Sinica,2006,32(4):603-617.(in Chinese)侯志強,韓崇昭.視覺跟蹤技術綜述[J].自動化學報,2006,32(4):603-617.
[2] GU Xin,WANG Haitao,WANG Lingfeng,et al.Fusing multiple features for object tracking based on uncertainty measurement[J].Acta Automatica Sinica,2011,37(5):550-559.(in Chinese)顧鑫,王海濤,汪凌鋒,等.基于不確定性度量的多特征融合跟蹤[J].自動化學報,2011,37(5):550-559.
[3] F Porikli,O Tuzel,PMeer.Covariance tracking using model update based on lie algebra[J].IEEE Computer Vision and Pattern Recognition,2006,pages:728-735.
[4] LI Shaojun,LI Liren,LIU Zhongling,et al.Terminal guidance target tracking based on region covariance matrix[J].Laser&Infrared,2010,40(3):330-333.(in Chinese)李少軍,李立仁,劉忠領,等.基于區域協方差矩陣的末制導目標跟蹤[J].激光與紅外,2010,40(3):330-333.
[5] F Porikli.Integral histogram:a fast way to extract histograms in cartesian spaces[J].IEEE Conf.on Computer Vision and Pattern Recognition,2005,829-836.
[6] W Forstner,B Moonen.A metric for covariance matrices technical report,dept of geodesy and geoinformatics[J].Stuttgart University,1999.

