鐵路鋼軌視覺識別檢測方法

王前選 ，梁習鋒 ，劉應龍，魯寨軍 ，彭燦

(1. 中南大學 軌道交通安全教育部重點實驗室，湖南 長沙，410075；2. 中南大學 交通運輸工程學院，湖南 長沙，410075；3. 軌道交通安全協同創新中心，湖南 長沙，410075；4. 湖南科創信息技術股份有限公司，湖南 長沙，410009)

確保列車運行安全是鐵路運輸永恒的主題，然而，我國地理環境復雜、氣候變化多樣，特別是新疆、內蒙古、青海、西藏等西北部地區鐵路經常受到大風、風沙、暴雪的侵襲，引起的沙雪等異物入侵事件嚴重威脅著列車運行安全[1-3]。在新疆蘭新(蘭州—新疆)鐵路了墩、十三間房等路段，由大風引起的沙雪等異物入侵事件曾多次造成列車脫軌翻車事故：因此，對沙雪等異物入侵事件監測是鐵路安全監測的重要內容之一[4-5]。隨著機器視覺技術的發展，視頻監測在鐵路安全監測中的應用越來越廣泛[6]，然而，國內外學者利用視頻圖像技術對沙雪等異物入侵事件監測的研究較少[7-9]。對沙雪等異物入侵事件監測的前提是對監測圖像中鐵路鋼軌進行準確識別[10-11]，其識別的正確率直接影響監測結果的有效性。利用數字圖像處理的方法正確識別鋼軌，首先要分析鋼軌在監測圖像中的特征。鋼軌在監測圖像中具有3 個特征[12]：(1) 材質一致、磨損基本均勻，在同一幅圖像中，鋼軌表面灰度基本一致；(2) 鋼軌與路基、枕木等其他設施的光照反射率不一致，鋼軌邊緣具有很強的灰度邊緣特征；(3) 鋼軌在監測圖像中表現為長且連續的線。基于鋼軌在監測圖像中的特征，采用數字圖像處理對鋼軌進行識別檢測得到了廣泛研究，然而，目前的鋼軌識別檢測方法在監測圖像背景復雜的情況下仍然包含較多的非鋼軌物體。為此，本文作者結合Radon 變換思想，推導出用于鋼軌識別檢測的Bresenham 直線算法，提出鋼軌直線檢測實現方法。在此基礎上，得到一種基于圖像處理的鋼軌識別檢測方法，蘭新(甘肅蘭州—新疆烏魯木齊)鐵路現場試驗驗證了鋼軌識別檢測方法的計算效果。

1 基于Radon 變換的鋼軌檢測流程

1.1 Radon 變換

1個n 維函數f (x1, x2, x3, …, xn)的Radon 變換[13-15]定義為n-1 維超平面上的積分值。當n=2 時，Radon變換是計算圖像在某一指定角度射線方向上的投影變換，即圖像在確定方向上的線積分，反映了圖像在不同方向上的投影性質。二維平面函數 I (x , y)的Radon變換原理如圖1 所示，變換公式如下：

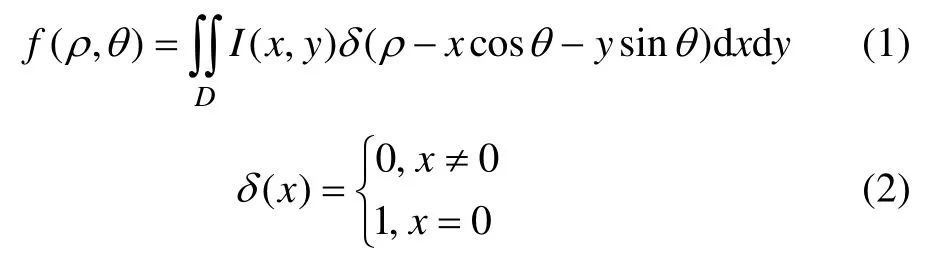
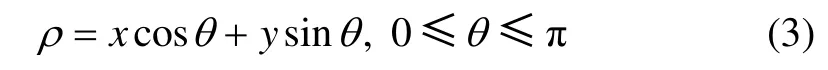
式中：D 為整個圖像平面；I(x,y)為圖像上點的灰度；θ 為投影線與水平軸的夾角；δ 為Direact 函數；ρ 為函數f(x,y)上的點在投影線的投影點到中心點的距離。Radon 變換將圖像從灰度平面映射到參數(ρ ,θ)平面，對圖像函數求出各個θ 的投影，從而對圖像進行全角度觀察。若圖像中存在直線，則直線在法線方向投影最大，在參數平面(ρ0,θ0)處該直線會形成1 個峰值，通過提取峰值對應的(ρ0,θ0)，可以得到圖像平面中直線的斜率和偏移量。

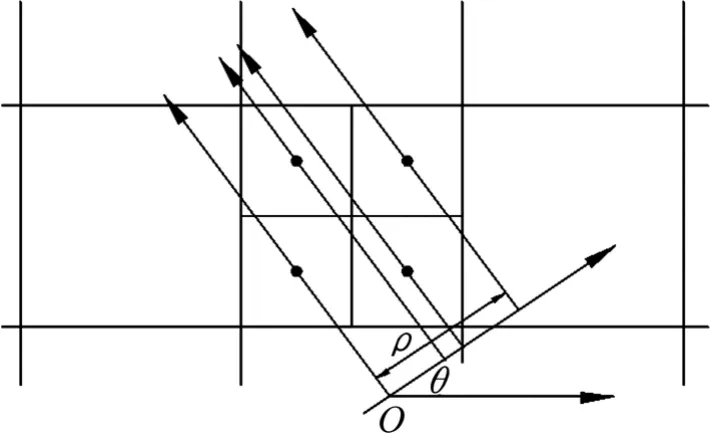
圖1 Radon 變換原理Fig.1 Principle of Radon transform

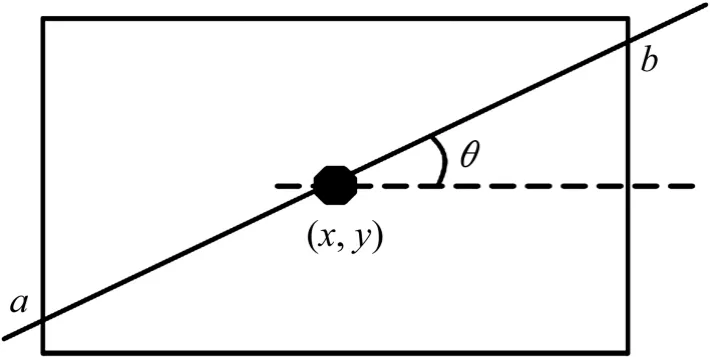
圖2 圖像中心點和角θ 的選取Fig.2 Choice of image center point and θ

1.2 鋼軌檢測算法流程

在Radon 變換中，選取圖像的中心坐標(x,y)作為計算基點，角θ 的取值為經過中心點的直線與X 軸正方向之間的夾角，圖像中心點與角θ 的選取如圖2 所示。該角度的取值范圍為-90°～90°，算法計算步長為1°。對每個角度，沿經過圖像中心點、與X 軸呈該角度的直線ab 對灰度進行積分，并用參與積分的像素個數進行歸一化，然后對積分進行差分。若該角度下存在差分的絕對值最大值大于10，即可認為該角度存在直線，差分最大值在差分向量中的位置反映了該直線在圖像中的位置。由于直線方程y=mx+b 的斜率是角度θ 的正切值，而b 可由差分最大值在差分向量中的位置計算得到，所以，鋼軌的直線方程可以由此確定。鋼軌檢測算法流程如圖3 所示。

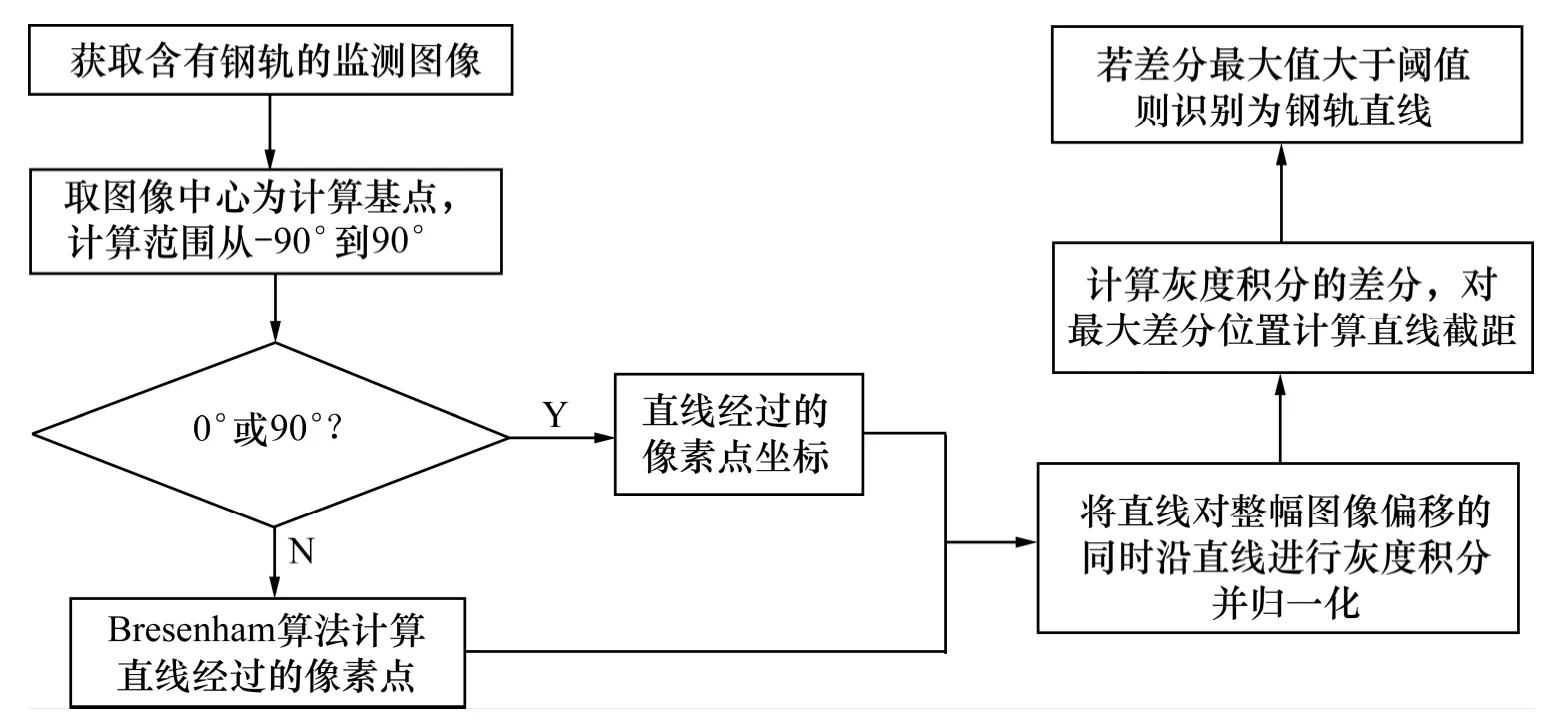
圖3 鋼軌檢測算法流程Fig.3 Process of railway rail detection algorithm

2 坐標系定義與轉換

在計算監測圖像中的鐵路鋼軌直線方程y=mx+b過程中，涉及到歐幾里得坐標系和圖像坐標系。歐幾里得坐標系的原點在圖像的左下角，X 軸的正方向水平向右，Y 軸的正方向垂直向上，而圖像坐標系的坐標原點在圖像的左上角，X 軸的正方向水平向右，Y軸的正方向垂直向下，因此，歐幾里得坐標系與圖像坐標系的轉換方程為：

其中：(xe, ye)為歐幾里得坐標系坐標；(xp, yp)為圖像坐標系坐標；nrow為監測圖像的行數。

3 Bresenham 直線檢測算法

3.1 Bresenham 算法推導

當選取1 個角度θ，確定直線ab 后(如圖2 所示)，為了沿ab 對像素灰度進行積分，采用Bresenham 算法計算出該直線y=mx+b 經過哪些像素。Bresenham 算法是計算機圖形學中為“顯示器(屏幕或打印機)系由像素構成”的這個特性而設計出來的算法，使得在求直線各點的過程中全部以整數來運算。其原理是：過各行、各列像素中心構造一組虛擬網格線，按直線從起點到終點的順序計算直線各垂直網格線的交點，然后確定該列像素中與此交點最近的像素。直線ab 斜率0＜m＜1 時，Bresenham 算法推導過程如下(當直線ab斜率m＞1，-1＜m＜0 和m＜-1 時的推導過程類似)。直線ab 斜率在0＜m＜1 時的示意圖見圖4。

圖4 中黑色圓點的y 為

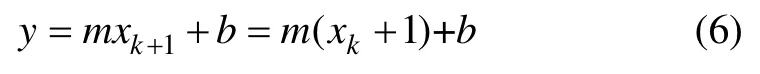
其與像素yk+1的距離為

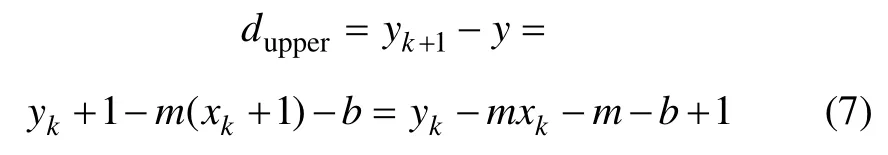
與像素yk的距離為

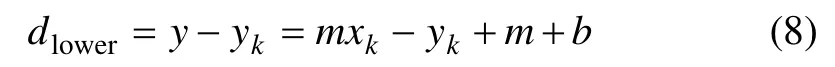
兩者之差為

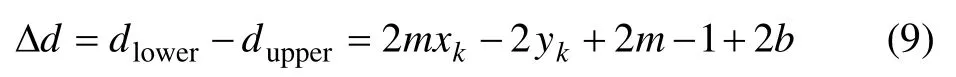
令m=Δy/Δx

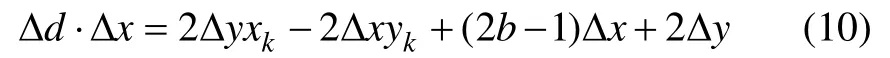
令pk=ΔdΔx ，則

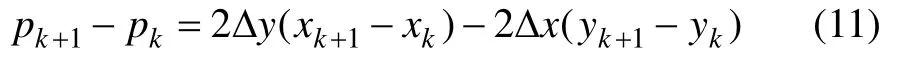
即

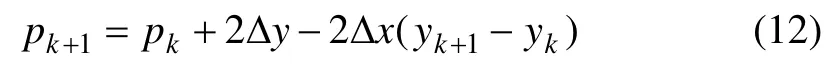
當 Δd ＞0 時，pk＞0，黑色圓點離像素yk+1更近，yk+1取為yk+1，則

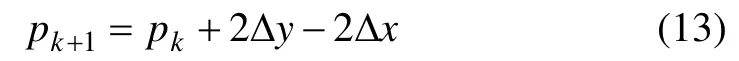
當 Δd ＜0 時，pk＜0，黑色圓點離像素yk更近，pk＜0，yk+1取為yk，則

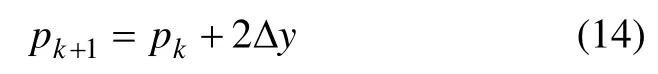
遞推關系式(13)和(14)與yk+1的取值直接關聯，決定了直線下一個像素值的位置。 Δx 和 Δy 是直線2 個端點之間的坐標差值，將m=Δy/ Δx 代入Δd?Δx，可得

3.2 直線段端點的選取

為保證在Bresenham 算法中P1點在P2點左邊，需根據圖像的對角線角度對直線進行分類。首先判斷直線是否為垂直線或水平線，若是，則按橫坐標都相同或縱坐標都相同輸出坐標點，其余的情況如圖5 所示。圖5 中，P1和P2的坐標均為圖像坐標系下的坐標，ncol，nrow分別為點P1或點P2的x 坐標、y 坐標的值。

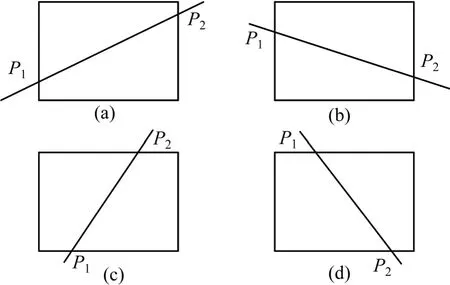
圖5 直線與圖像邊緣交點情況Fig.5 Intersections situations between straight line and image edge

從圖5(a)和圖5(b)可見：當0＜θ≤arctan(nrow/ncol)，-arctan(nrow/ncol)≤θ＜0 時，P1為直線ab 與圖像第1列的交點，x 坐標為1，y 坐標為tan θ·1+b；P2為直線ab 與圖像最后1 列的交點，x 坐標為ncol，y 坐標為tan θ·ncol+b(其中，ncol為圖像的列數)。從圖5(c)可見：當θ＞arctan(nrow/ncol)時，P1為直線ab 與圖像最下面1行的交點，y 坐標為nrow，x 坐標為(nrow-b)/tan θ；P2為直線ab 與圖像最上面1 行的交點，y 坐標為1，x坐 標 為(1-b)/tan θ。從 圖 5(d)可 見：當 θ ＜-arctan(nrow/ncol)時，P1為直線ab 與圖像最上面1 行的交點，即y 坐標為1，x 坐標為(1-b)/tan θ；P2為直線ab 與圖像最下面1 行的交點，y 坐標為nrow，x 坐標為(nrow-b)/tan θ。

3.3 Bresenham 算法實現

按上述直線段端點的選取方法選取直線ab 與圖像相交的2 個端點P1和P2，其中點P1在點P2的左端。

第1 步：計算2 點之間的坐標值差異 Δx 和 Δy ：

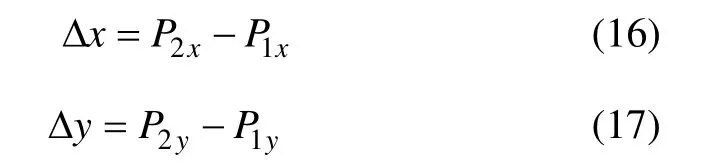
第2 步：計算初始值p0。

當直線ab 斜率0＜m＜1 和m＞1 時，

當直線ab 斜率-1＜m＜0 和m＜-1 時，

第3 步：對貫穿圖像的每個x 或y，計算Pk+1。

(1) 當直線ab 斜率0＜m＜1 時，對貫穿圖像的每個x，若 Pk＜0，則

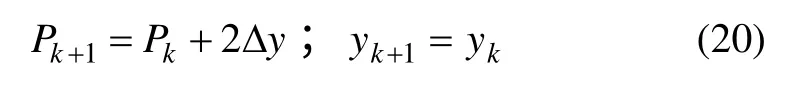
若 Pk＞0，則

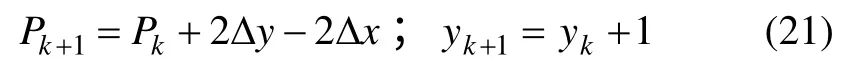
(2) 當直線ab 斜率m＞1 時，對貫穿圖像的每個y，若 Pk＜0，則

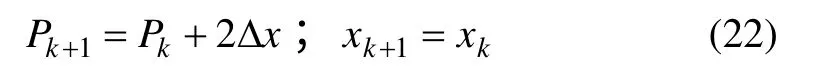
若 Pk＞0，則

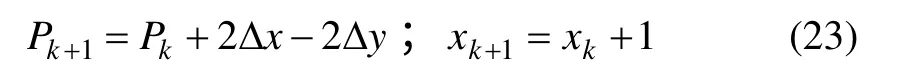
(3) 當直線ab 斜率-1＜m＜0 時，對貫穿圖像的每個x。若 Pk＜0，則

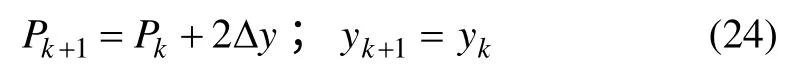
若 Pk＞0，則

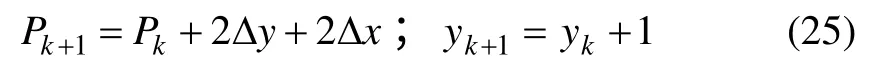
(3) 當直線ab 斜率m＜-1 時，對貫穿圖像的每個y。若 Pk＜0，則

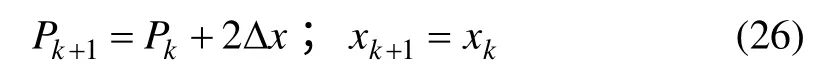
若 Pk＞0，則

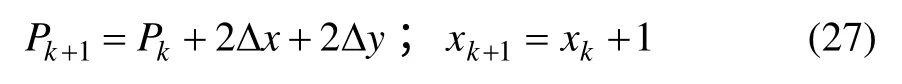
4 直線檢測算法實現

在執行完Bresenham 直線檢測算法后，得到圖像中每個角度對應的經過圖像中心的直線，并得到該直線經過的所有像素點坐標值。將該直線對整幅圖像偏移，同時沿該直線對像素值進行積分，如圖6 所示。

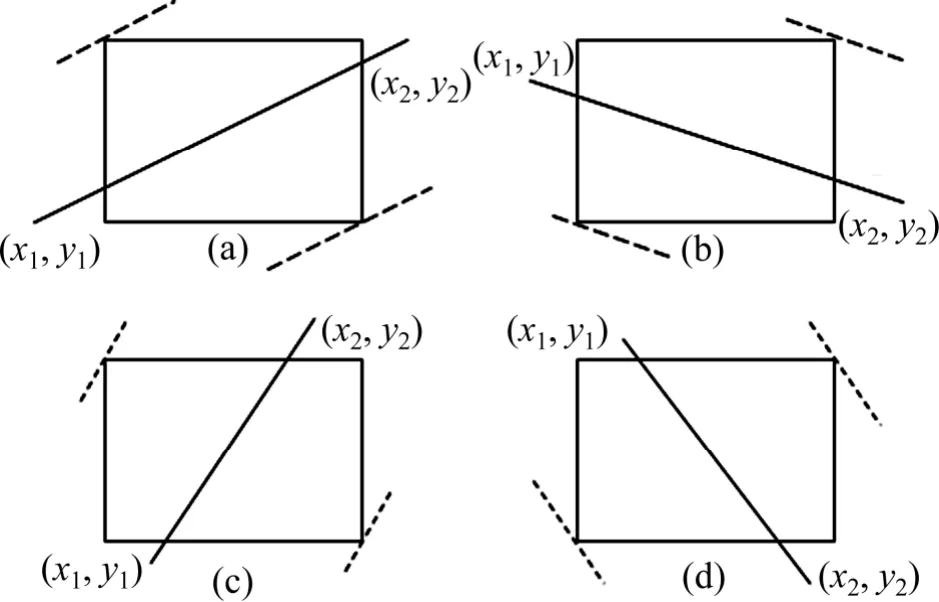
圖6 直線偏移的4 種情況Fig.6 Four cases of linear migration

如圖6(a)和圖6(b)所示，直線在圖像中作垂直偏移。每次偏移后，像素點的x 坐標不變，y 坐標加1或減1，y 坐標的偏移量分別為[-y1，nrow-y2]和[nrow-y1，y2]；如圖6(c)和圖6(d)所示，直線在圖像中進行水平偏移，每次偏移后，像素點的y 坐標不變，x 坐標加1或減1，x 坐標的偏移量均為[-x2，ncol-x1]。圖中直線每偏移1 次，則沿該直線進行像素值進行積分，同時計算參與積分的像素個數，并將積分值除以像素個數予以歸一化。當直線偏移到圖像的兩端時，直線的一部分會超出圖像界限，在計算中令此種點的像素值為0，僅有較少的圖像像素參與計算，所得的歸一化數據很大，這會對積分最大值的正常選取造成干擾，因此，對偏移到直線兩端的n 個位置不予計算，n 的取值應根據實際情況合理選取。

對圖像沿特定角度的直線進行積分，得到1 個像素值累加平均值的向量，對該向量進行差分，得到1個差分向量。當差分的絕對值大于一定值N 時，則在圖像中檢測到直線，N 的取值取決于所處理的圖像。該最大值在向量中的位置對應檢測到的直線在圖像中的位置，該位置可用于計算直線相對于經過圖像中心點直線的偏移量。直線的斜率是角度θ 的正切值，將直線上的任意一點代入直線方程可得出直線截距。

5 計算結果與分析

為了驗證鋼軌檢測算法的檢測效果，在蘭新鐵路進行現場試驗，攝像機和照明光源云臺安裝在蘭新鐵路紅層車站西約800 m上行線編號為0650的接觸網立柱上，現場安裝如圖7 所示，由現場攝像機拍攝的監測圖像如圖8 所示。

圖7 攝像機和照明光源現場安裝Fig.7 Field installation of camera and lighting light source

圖8 現場監測圖像Fig.8 Field monitoring image

對圖8 中2 條鋼軌進行灰度積分，等同于將圖中2 條鋼軌沿順時針旋轉至與X 軸垂直，然后，將整幅圖像對X 軸進行投影再進行積分。旋轉后的圖像如圖9 所示，圖像平均灰度曲線如圖10 所示，積分得到的灰度向量和差分向量分別如圖12 和圖13 所示。

由圖10 可以看出：圖像平均灰度曲線在中間部分有2 個明顯峰值，該2 個峰值即對應圖中1 號和2 號鋼軌位置的平均灰度。在圖像邊緣部分，由于參與積分的像素較少，平均后的像素值波動將較大，為了不發生鋼軌直線位置誤判，在圖像處理過程中將差分的最初n 個點和最后n 個點去掉(本次計算n=30)，則可得出理想的積分向量的差分向量曲線。鋼軌所在直線檢測結果如圖12 和圖13 所示。

圖9 旋轉后的監測圖像Fig.9 Monitoring images after rotation

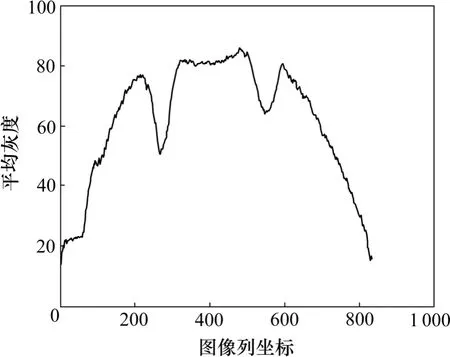
圖10 圖像平均灰度Fig.10 Average gray value of image

圖11 計算結果Fig.11 Calculation result

由圖12 可以看出：圖12(a)中的曲線峰值是1 號鋼軌所在直線的積分值，圖12(b)中曲線峰值即差分最大值則對應著1 號鋼軌直線所在位置。

由圖13 可以看出：圖13(a)中的曲線峰值是2 號鋼軌所在直線的積分值，圖13(b)中曲線峰值即差分最大值則對應著2 號鋼軌直線所在位置。從圖10 可以看出：由本文提出的鐵路鋼軌視覺檢測算法計算得出的2 條直線準確落在監測圖像中的2 條鋼軌上。在圖像坐標系下，1號和2號鋼軌所在直線的檢測結果見表1。

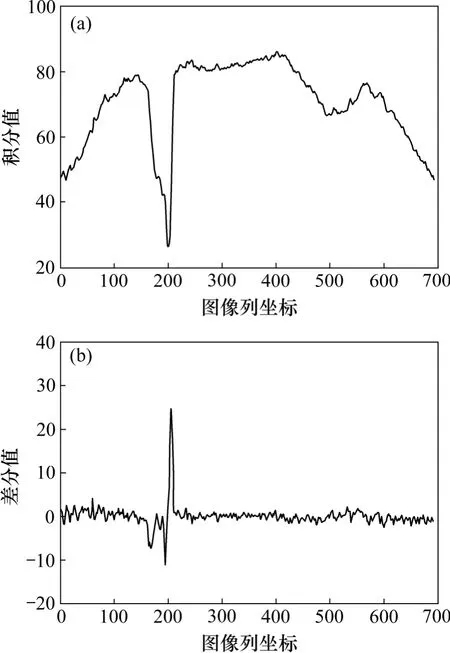
圖12 1 號鋼軌檢測結果Fig.12 No.1 rail test results

圖13 2 號鋼軌檢測結果Fig.13 No.2 rail test results

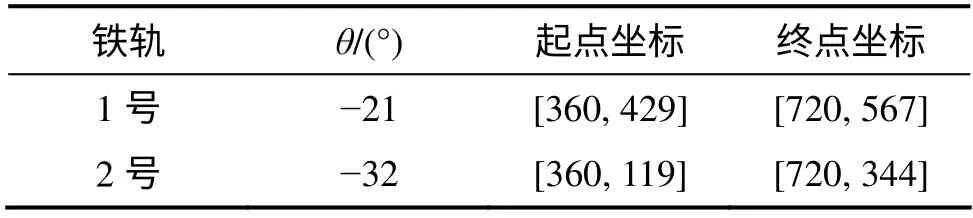
表1 鋼軌直線檢測結果Table 1 Test results of rail lines

據表1，在圖像坐標系下，由兩點式可求出2 條鋼軌所在的直線方程。兩鋼軌直線方程分別為：

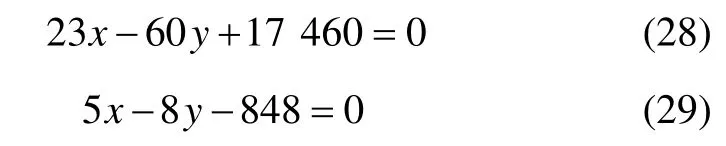
6 結論

(1) 基于鋼軌在監測圖像中的特征，提出了一種基于Radon 變換思想和Bresenham 直線檢測算法的鐵路鋼軌識別檢測方法。

(2) 在蘭新鐵路現場試驗計算得出的2 條直線準確落在監測圖像中的兩鋼軌上，并計算得出了在圖像坐標系下的2 條鋼軌直線方程。

(3) 該方法可準確檢測出監測圖像中鋼軌所在的直線，即可準確識別檢測出監測圖像中的鐵路鋼軌，為準確監測沙雪等異物入侵事件提供了必要支撐。

[1] Maneesha S, Sameer S, Jay J, et al. Autonomous rail track inspection using vision based system[C]// IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety. Alexandria, USA, 2006: 56-59.

[2] Bogdan S, Andrzej C. Fast detection and impulsive noise removal in color images[J]. Real Time Imaging, 2005, 11(5/6):389-402.

[3] 何茜. 基于雙目立體視覺的高速鐵路異物侵限檢測系統研究[D]. 北京: 北京交通大學機械與電子控制工程學院, 2012:1-6.HE Xi. Research on clearance intrusion detection system for high-speed railway based on binocular stereo vision[D]. Beijing:Beijing Jiaotong University. School of Mechanical and Electronic Control Engineering, 2012: 1-6.

[4] 胡慶武, 陳智勇, 吳莎. 基于移動雙目視覺的鐵路建筑物限界快速自動檢測方法[J]. 鐵道學報, 2012, 34(1): 66-71.HU Qingwu, CHEN Zhiyong, WU Sha. Fast and automatic railway building structure clearance detection technique based on mobile binocular stereo vision[J]. Journal of the China Railway Society, 2012, 34(1): 66-71.

[5] Davey J, Wallace A, Stenson N, et al. The experiences and perceptions of heavy vehicle drivers and train drivers of dangers at railway level crossings[J]. Accident Analysis and Prevention,2008, 40(2): 1217-1222.

[6] Susumu K, Tsuyoshi N, Yasukazu O. A global optimization algorithm for real-time onboard stereo obstacle detection systems[C]// Proceedings of the 2007 IEEE Intelligent Vehicles Symposium Istanbul. Turkey, 2007: 13-15.

[7] 同磊. 基于機器視覺的軌道交通線路異物檢測技術研究[D].北京: 北京交通大學機械與電子控制工程學院, 2012: 23-40.TONG Lei. A study on railway obstacle detection using machine vision[D]. Beijing: Beijing Jiaotong University. School of Mechanical Electronic and Control Engineering, 2012: 23-40.

[8] 同磊, 朱力強, 余祖俊, 等. 基于車載前視攝像機的軌道異物檢測[J]. 交通運輸系統工程與信息, 2012, 12(4): 79-84.TONG Lei, ZHU Liqiang, YU Zujun, et al. Railway obstacle detection using onboard forward-viewing camera[J]. Journal of Transportation Systems Engineering and Information Technology,2012, 12(4): 79-84.

[9] 王志斌. 哈大鐵路客運專線雪深監測系統研究[J]. 鐵道標準設計, 2012(5): 165-168.WANG Zhibin. Approach to snow depth detecting system on Harbin-Dalian passenger dedicated line[J]. Railway Standard Design, 2012(5): 165-168.

[10] 柴世紅. 基于邊緣檢測的鐵軌識別[J]. 鐵路計算機應用, 2009,18(4): 1-3.CHAI Shihong. Railway recognition based on edge detection[J].Railway Computer Application, 2009, 18(4): 1-3.

[11] 關鵬, 顧曉東, 張立明. 一種基于圖像處理的鐵軌自動檢測方法[J]. 計算機工程, 2007, 33(19): 207-210.GUAN Peng, GU Xiaodong, ZHANG Liming. Automatic railroad detection approach based on image processing[J].Computer Engineering, 2007, 33(19): 207-210.

[12] 鄭河榮, 熊麗榮, 王天舟. 基于HOUGH 變換的二維條碼圖像矯正[J]. 浙江工業大學學報, 2003, 31(2): 169-172.ZHENG Herong, XIONG Lirong, WANG Tianzhou. Study on 2D-Barcode image slant correction based on HOUGH transform[J]. Journal of Zhejiang University of Technology,2003, 31(2): 169-172.

[13] 胡東紅, 譚輝, 陳莘萌. Radon 變換在二維條碼圖像識別中的應用[J]. 武漢大學學報(理學版), 2005, 51(5): 84-88.HU Donghong, TAN Hui, CHEN Xinmeng. The application of Radon transform in the 2D-Barcode image recognition[J].Journal of Wuhan University (Natural Science Edition), 2005,51(5): 84-88.

[14] 馬婧, 徐守時, 陳克. 基于Radon 變換的圖像角點角度提取算法[J]. 光電工程, 2009, 36(2): 126-131.MA Jing, XU Shoushi, CHEN Ke. Method of angles picked-up of corners in images based on radon transform[J].Opto-Electronic Engineering, 2009, 36(2): 126-131.

[15] 林萌, 李翠華, 黃劍航. 基于Radon 變換的運動模糊圖像參數估計[J]. 計算機技術與發展, 2008, 18(1): 33-36.LIN Meng, LI Cuihua, HUANG Jianhang. Parameters estimation of motion blurred images based on radon transform[J]. Computer Technology and Development, 2008, 18(1): 33-36.