考慮交通管理策略的交叉口信號控制多目標優化

龍瓊 ，胡列格，張謹帆，周昭明，彭爍

(1. 湖南城市學院 土木工程學院，湖南 益陽，413000；2. 長沙理工大學 交通運輸工程學院，湖南 長沙，410004)

隨著城市人口數量的不斷增長和人們物質生活水平的逐漸提高，機動車保有量迅猛增長，進而使道路交通需求急劇增加，交通擁堵問題日益凸顯。針對交通擁堵問題，僅僅通過加強交通基礎設施的建設是難以解決的，而根據實際交通狀況實時優化交通信號控制方案是一種有效緩解交通擁堵的手段。交叉口作為城市交通網絡中的重要組成部分，是城市交通擁擠的主要發生地，所以，針對城市道路交叉口交通信號控制問題開展研究，對于改善城市道路交通擁堵狀況、提高道路通行能力、減少交通事故、減少交通環境污染等方面具有十分重要的現實意義。交通信號控制是調控路網交通流運行的主要交通管理措施之一，應體現安全、通暢、高效等多方面的控制意圖[1]。在優化交通信號協調控制參數時，需要考慮交通管理策略，權衡平均延誤時間、排隊長度、通過流量等指標[2-3]，因此，交通信號控制問題是一個考慮交通管理策略的多目標優化問題。近年來，采用多目標優化方法研究城市道路交通信號控制問題已成為研究熱點。早期的多目標優化是Akcelik[4]在F-B 法的基礎上引入停車補償系數，結合車輛延誤時間參數，共同評價信號配時的優化程度。Vincent 等[5]以TRANSYT 系統為對象，將延誤時間和停車次數轉換為燃油消耗指標，基于爬山法和遺傳算法對模型求解。常健等[6]建立了車輛排隊延誤和路段行程時間的加權線性組合優化模型，求解獲得控制參數，并定性地探討了權重系數與優化目標之間的變化關系。Zeng 等[7]基于元胞傳輸模型，模擬車流在道路交叉口的運行規律，建立了以平均延誤和通行能力為優化目標的多目標優化模型，采用MOGA 多目標遺傳算法進行了模型求解。曹成濤等[8]引入交通控制飽和度約束，建立了以機動車流的平均延誤、平均停車次數和總通過流量為優化目標的加權組合優化模型，基于遺傳算法對模型進行求解。高云峰等[1]以交叉口群為對象，建立了交通信號協調控制參數的多目標優化模型，基于非支配排序遺傳算法設計了相應的多目標優化算法求解模型。但是，由于實際交通系統的復雜性和多變性，交通狀況難以精確描述，多目標優化模型往往通過簡單加權來轉化為單目標優化模型進行求解，忽略了交通管理者對交通流疏導的策略和意圖，因而，這類多目標優化模型往往難以適應實際復雜多變的城市道路交通系統控制需求。為此，本文作者面向復雜多變的交通系統控制需求，充分考慮交通管理者對交通疏導的控制策略，基于模糊分析法(fuzzy analytic process，FAP)設計了一種城市道路交叉口信號控制多目標優化模型，同時，考慮Q 學習算法具有快速收斂特性的同時，無需過多顧及環境指標的動態變化，基于Q 學習算法對多目標優化模型進行求解，從而實時產生考慮交通管理者策略的交叉口信號控制方案。

1 基于FAP 的多目標優化模型

1.1 交叉口優化模型

交叉口交通信號控制優化模型的評價指標一般為單位時間內通過的車流量最大、車輛總延誤時間最短、車輛排隊長度最短、車輛在交叉路口的平均停車次數最少等，控制模型根據交通控制目標構造評價函數，結合交通管理者的控制意圖，對交叉口進行優化控制。以典型的平面十字交叉城市道路口為例，本文選用排隊長度l、延誤時間d 和停車次數n 作為模型優化評價指標，構建綜合評價指標函數為

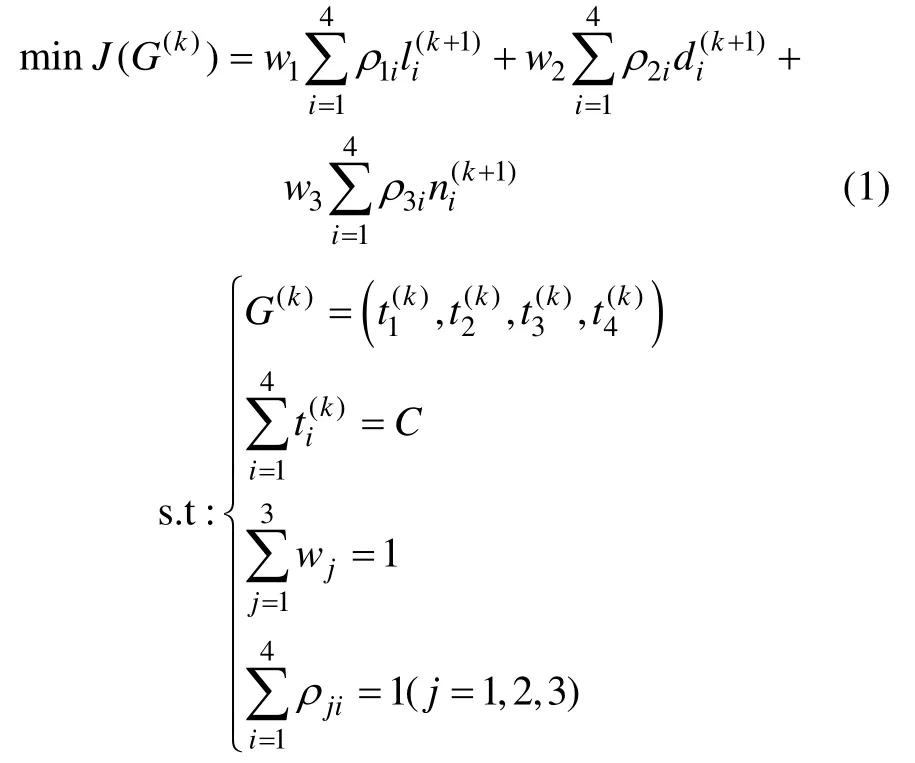
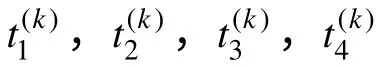
值得說明的是：在模型(1)中，排隊長度l、延誤時間d 和停車次數n 的量綱不同，在實際操作過程中，需要經過統一歸一化處理。同時，在模型中，wj和 ρji體現了交通管理者對指標和相位的重視程度，而交通管理者的認識本身具有主觀性和模糊性，增加了模型求解的復雜程度。本文考慮引入模糊分析法(FAP)對這些權重系數進行量化，從而簡化交通管理者判斷交通優化指標相對重要性的復雜過程，解決交通指標優化排序過程中的一致性問題，使優化模型更好地反映交通管理者的控制需求。

1.2 基于FAP 的權重系數確定

實際問題往往具有復雜性和模糊性，用模糊數表示判斷的結果能夠更好地反映事物的客觀本質。因此，本文在權重確定過程中引入模糊數學理論，即應用模糊分析法對交通優化模型進行權重確定。與一般方法相比，模糊分析法簡化了人們判斷評價相對重要性的復雜程度，解決了權重確定過程中的一致性問題。

基于模糊分析法進行權重確定的基本過程是[9-10]：在構建交叉口優化模型的基礎上，以矩陣形式表達各單項優化指標的相對重要性，從而建立相應的模糊矩陣：

其矩陣元素按如下的模糊邏輯確定：

對模糊矩陣F 進行一致化處理，構成模糊一致矩陣：

其中，rij按照如下方式確定：

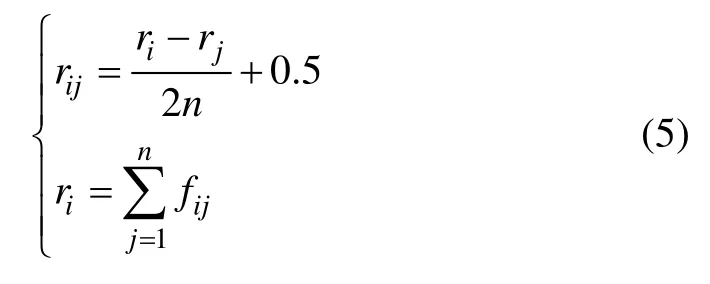
然后進行權重確定，即根據模糊一致矩陣計算對于交通管理者而言的指標重要性相對權重(不含自身比較)：

進行歸一化后可得

基于上述思想，對于交叉口優化模型(1)，交通管理者根據交通管理策略，僅需確定排隊長度l、延誤時間d 和停車次數n 等指標的相對重要性，就可確定相應的指標權重wj(j=1, 2, 3)。同理，對于各優化指標在不同相位的權重系數 ρji，亦可以通過類似方法確定，由此可以看出：基于模糊分析方法，交通管理者僅需兩兩比較優化指標的相對重要性，大大降低了交通管理者根據自身意圖來設置指標權重的復雜程度，且該方法還能夠有效保證權重確定過程中的一致性問題。

2 基于Q 學習的模型優化

2.1 Q 學習算法

Q 學習算法最早在1989 年由Watkins 等提出[11]，是模擬動物學習行為的一種強化學習算法，該算法因操作簡單且收斂性好而受到研究者的重視。Q 學習算法通過從環境中得到獎懲的方法來獲得不同狀態下的最優策略。Q 學習的積累回報函數 Q (s , a)是指在狀態s 執行完動作a 后希望獲得的積累回報，它取決于當前的立即回報和期望的延時回報。

在Q 學習算法中，模型通過不斷反射學習優化1個可以迭代計算的Q 函數提高學習能力，Q (s , a)函數的初始值可任意給定，其學習規則為[12]

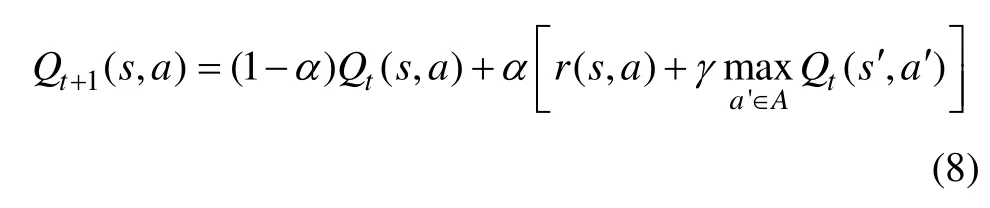
式中：α ∈[ 0,1]為學習速率； γ ∈[ 0,1]為折扣因子；a為所有可供選擇的動作的集合；r (s, a)為回報函數值；Qt(s ′, a′)為在下一個狀態s’時系統選擇任何行為a′的Q 函數值。

Q 學習算法不同于其他學習算法[13]的是不需要建立面向外部狀態環境變化的模型，適合于在線學習。近年來，Q 學習在人工智能、機器學習等領域取得了諸多研究成果，在此，本文采用Q 學習算法用于求解交叉口的信號控制優化問題。

2.2 基于Q 學習的交叉口模型優化

根據交叉口模型(1)，控制參數集和決策參數集可以分別表達為：

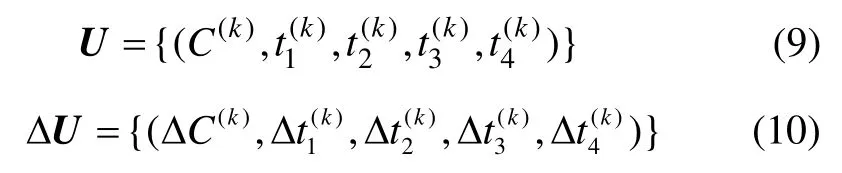
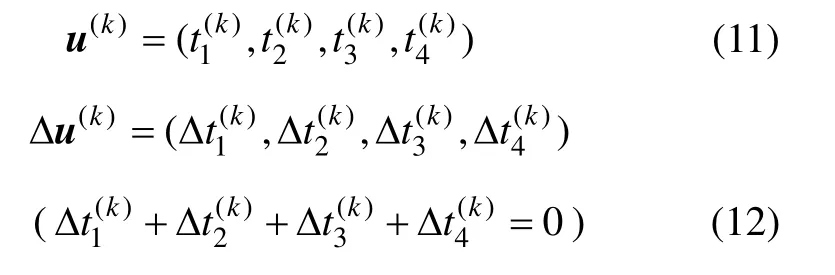
同時，在實際交通信號控制中，信號燈時間通常以秒(s)為單位計時，因而，控制參數集U 和決策參數集ΔU 均為有限可數集合。這給Q 學習算法的應用帶來了方便。

根據模型(1)，設計收益函數如下：

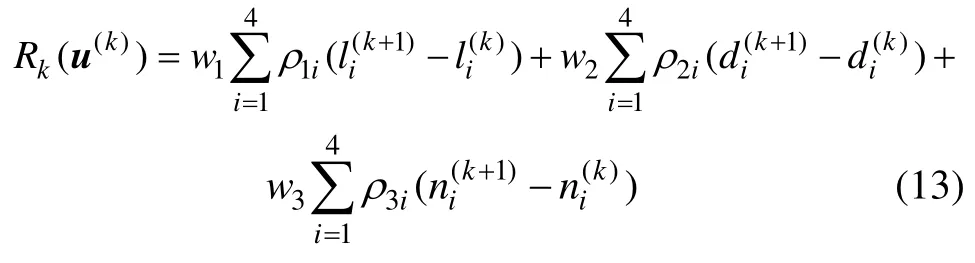
在權重系數wj和 ρji確定后，下面參照文獻[14]并作以改進，設計獲得相應的交通信號控制策略。

2.2.1 初始控制參數

初始控制參數的確定依據

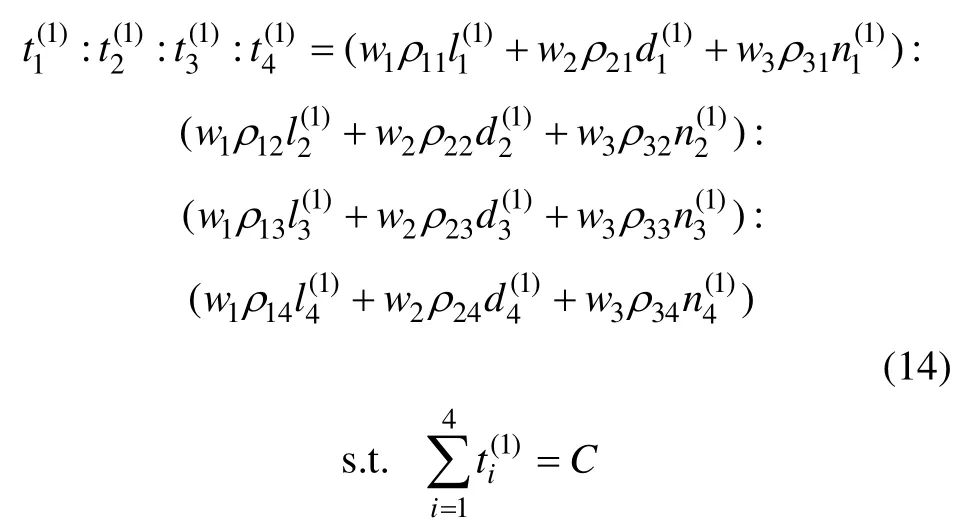
2.2.1 過程控制策略

在第k+1 個周期個控制周期，控制策略設計如下。

(1) 若Rk(u(k))＜0，則說明控制系統趨于收斂，交通狀況漸趨通暢，

(2) 若Rk(u(k)) ＞0，則說明控制系統趨于發散，交通狀況漸趨惡化。令

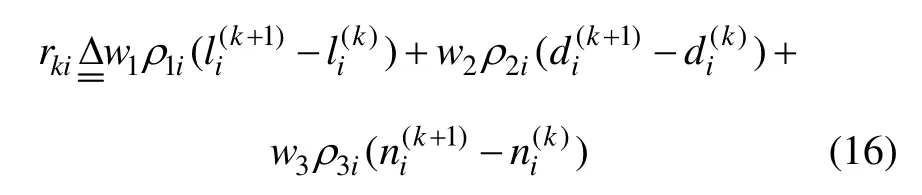
若對所有相位i=1, 2, 3, 4，均有rki＞0，則說明交通流量逐漸增大而導致交通系統整體惡化，此時，重新調整控制策略，依據下式

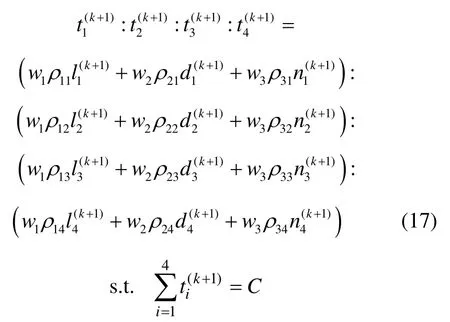
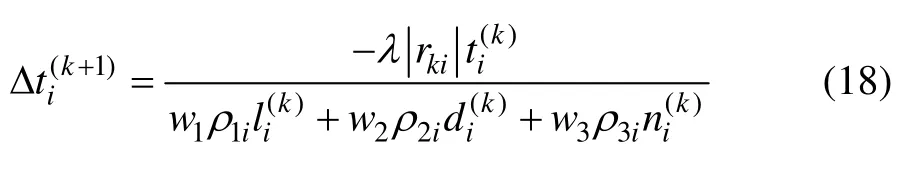
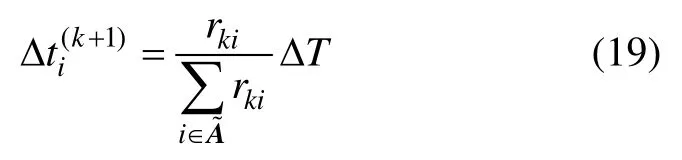
由此獲得Δu(k+1)，從而可求得第k+1 個周期的控制量u(k+1)。與文獻[14]相比，本文在此引入了保守因子λ，避免了對交通惡化相位的過度反應，保證了漸趨通暢相位的收斂性。

(3) 若Rk(u(k))=0，則說明交通整體狀況沒有發生變化，此時，對應的交叉口交通狀況是：部分相位惡化，部分相位向好(理論上存在所有相位交通狀況均沒有變化的情況)，參照情況(2)進行研究微調。

3 實驗仿真

為了驗證本文方法的有效性，以典型的十字交叉路口為例，針對如下2 種想定情況進行仿真實驗，并與傳統的定時控制方法進行對比。

(1) 情況1：不考慮交通管理策略。

在不考慮交通控制策略的情況下，交通管理者對各優化指標和相位無偏好，因此，在模型(1)中，權重系數取值為 w1=w2=w3=1/3，ρji=1/4(j=1, 2, 3;i=1, 2, 3, 4)。

(2) 情況2：考慮交通管理策略。

假設交通管理者面向大區域交通系統需求，設置其優化指標的相對重要性為：排隊長度相對重要性＞延誤時間相對重要性=停車次數相對重要性。

同時，大區域交通環境要求優先保障處于第1 和第2 相位的車輛通過，同時兼顧第3 和第4 相位車輛，則相位相對重要性設置為：第1 相位相對重要性=第2相位相對重要性＞第3 相位相對重要性=第4 相位相對重要性。

根據前面的權重系數確定方法，求得

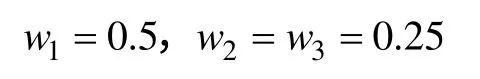
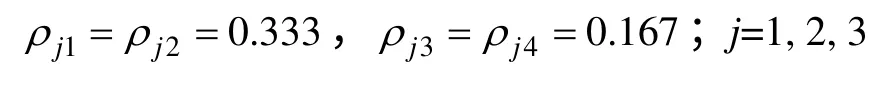
取控制周期C=120 s，保守因子λ=0.9，在不同交通流量下獲得的仿真結果如圖1～3 所示。

從圖1～3 可以看出：本文所提出的多目標優化控制算法能夠較大幅度地縮短排隊長度、延誤時間和減少停車次數，與傳統定時控制方法相比具有明顯的優勢，這種優勢隨著交通流量的增大更加明顯。

表1 所示為各種控制模型的各種具體控制結果。從表1 可以看出：在不同車流量條件下，采用本文方法能夠有效減小排隊長度、延誤時間和停車次數，大大提高了交通系統的運行效率。特別地，根據情況2獲得的實驗結果，與第3 和第4 相位相比，第1 和第2 相位更加通暢，尤其是在不同車流量下，第1 和第2相位的排隊長度較短，較好地體現了交通管理者的控制意圖。

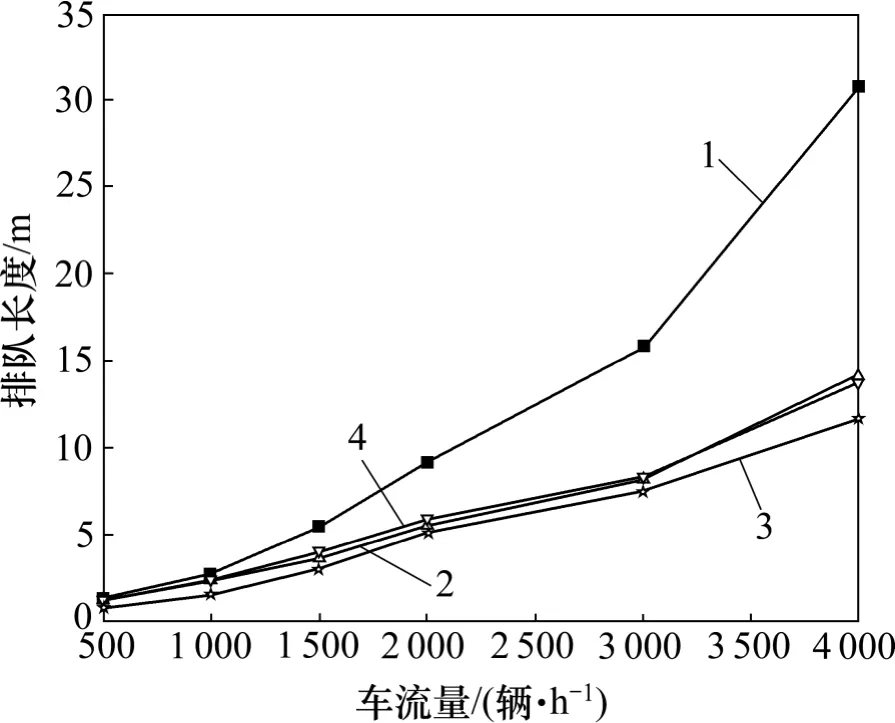
圖1 不同車流量條件下的排隊長度對比Fig.1 Comparison of queue length at different traffic conditions

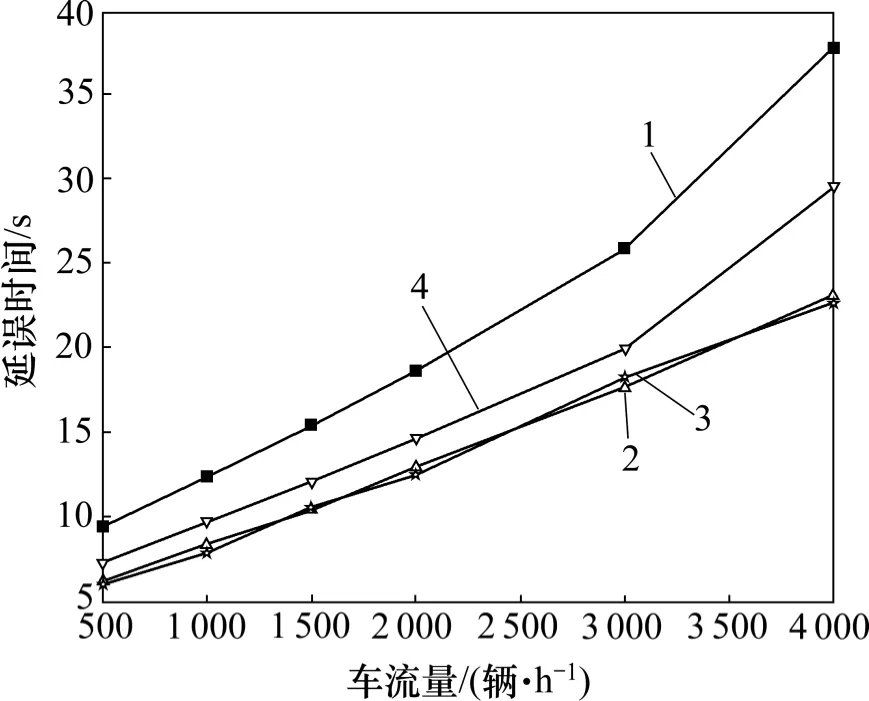
圖2 不同車流量條件下的延誤時間對比Fig.2 Comparison of delay time at different traffic conditions

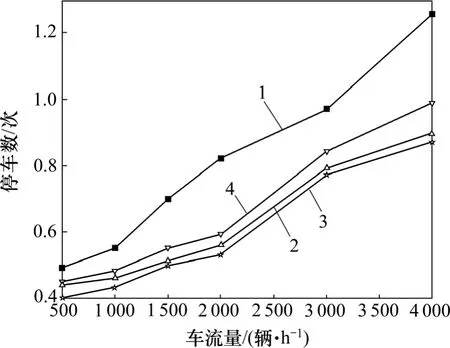
圖3 不同車流量條件下的停車次數對比Fig.3 Comparison of number of parking at different traffic conditions

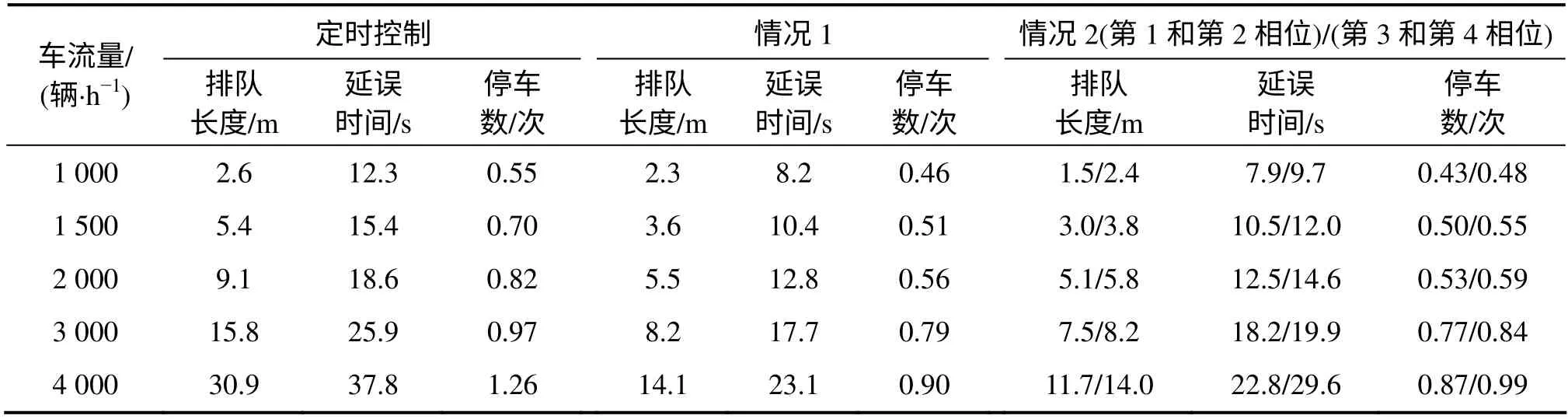
表1 不同車流量條件下的仿真結果比較Table 1 Comparision of simulation results at different traffic conditions

4 結論

面向復雜多變的交通系統控制需求，基于模糊分析法設計了一種城市道路交叉口信號控制多目標優化模型，并基于Q 學習算法對多目標優化模型進行求解，該方法具有如下特點：

(1) 在建模過程中，充分考慮了交通管理者對交通疏導的控制策略，有利于保持與大區域交通環境的一致性。

(2) 引入模糊分析法確定優化指標權重系數，簡化了人們判斷評價相對重要性的復雜程度，解決了權重確定過程中的一致性問題。

(3) 構建了交叉口多目標最優模型，克服了以往優化方法目標單一的缺點。仿真結果表明該模型能夠兼顧多種優化指標，獲得折中解。

(4) 基于Q 學習算法對多目標優化模型進行求解，簡化了求解過程，保證了求解結果的收斂性。

[1] 高云峰, 胡華, 韓皓, 等. 城市道路交叉口群信號協調控制多目標優化與仿真[J]. 中國公路學報, 2012, 25(6): 129-135.GAO Yunfeng, HU Hua, HAN Hao. Multi-objective optimization and simulation of groups of intersections’ signal coordinate control[J]. China Journal of Highway and Transport,2012, 25(6): 129-135.

[2] DAI Yujie, ZHAO Dongbin. A traffic signal control algorithm for isolated intersections based on adaptive dynamic programming[C]// Proceedings of 2010 International Conference on Networking, Sensing and Control (ICNSC 2010). Chicago,USA, 2010: 255-260.

[3] Abdulhai B. Reinforcement learning for true adaptive traffic signal control[J]. ASCE Journal of Transportation Engineering,2003, 129(3) : 278-285.

[4] Akcelik R. Traffic signals: Capacity and timing analysis, ARR No.123[R]. Vermont South, Australia: ARRB Transport Research Ltd, 1981: 26-29.

[5] Vincent R A, Mitchell A I, Robertson D I. User guide of transport, Version 8, TRRL Report LR888[R]. Crowthorne, UK:Transport and Road Research Labortory, 1980: 356-361.

[6] 常健, 吳大為. 多目標交叉口信號控制模型[J]. 大連理工大學學報, 2000, 40(6): 653-656.CHANG Jian, WU Dawei. Multi-objective model of intersection signal control[J]. Journal of Dalian University of Technology,2000, 40(6): 653-656.

[7] Zeng J Q, Wang J J, Liu K, et al. CTM-MOGA based crossroad traffic signal control[J]. Journal of University of Science and Technology of China, 2005, 35(2): 284-290.

[8] 曹成濤, 徐建閩. 單交叉口交通多目標控制方法[J]. 計算機工程與應用, 2010, 46(16): 20-22.CAO Chengtao, XU Jianmin. Multi-objective control method at single intersection[J]. Computer Engineering and Applications,2010, 46(16): 20-22.

[9] XU Runing, ZHAI Xiaoyan. Extention of the analytic hierarchy process in fuzzy environment[J]. Fuzzy Sets and Systems, 1992,52: 29-32.

[10] 汪培莊. 模糊集合論及其應用[M]. 上海: 上海科學技術出版社, 1986: 329-332.WANG Peizhuang. Fuzzy set theory and its applications[M].Shanghai: Shanghai Science and Technology Press, 1986:329-332.

[11] Watkins C, Dayan P. Technical note: Q-learning machine learning[M]. Kluwer Academic Publishers, Boston, 1992:279-292.

[12] 魏赟, 邵清. 基于Q-學習和粒子群算法的區域交通控制模型[J]. 系統仿真學報, 2011, 23(10): 2108-2111.WEI Yun, SHAO Qing. Regional traffic control model based on Q-learning and particle swarm optimization[J]. Journal of System Simulation, 2011, 23(10): 2108-2111.

[13] 席燕輝, 葉志成, 彭輝. 一種基于自適應粒子濾波的多層感知器學習算法[J]. 中南大學學報(自然科學版), 2013, 44(4):1397-1402.XI Yanhui, YE Zhicheng, PENG Hui. An algorithm for MLPs training based on adaptive particle filter[J]. Journal of Central South University (Science and Technology), 2013, 44(4):1397-1402.

[14] 崔吉峰, 乞建勛, 楊尚東. 基于粒子群改進BP 神經網絡的組合預測模型及其應用[J]. 中南大學學報(自然科學版), 2009,40(1): 190-194.CUI Jifeng, QI Jianxun, YANG Shangdong. Combined forecasting model based on BP improved by PSO and its application[J]. Journal of Central South University (Science and Technology), 2009, 40(1): 190-194.

[15] 馬躍峰, 王宜舉. 一種基于Q 學習的單路口交通控制方法[J].數學的實踐與認識, 2011, 41(24): 102-106.

[16] MA Yuefeng, WANG Yiju. A traffic control method for single intersection based on Q-learning algorithm[J]. Mathematics in Practice and Theory, 2011, 41(24): 102-106.