利用柱殼法求立體的體積

邱香蘭

(萍鄉學院，江西萍鄉 337000)

所以，本文討論一個封閉的平面圖形繞坐標軸或與坐標軸平行的直線旋轉得到一個立體時，求其體積的方法，其中坐標軸不在已知的平面圖形內。［1］中利用已知平行截面的面積求其旋轉體的體積有過探討，本文利用柱殼法來求簡便得多，也容易推廣。

1 定義及命題

旋轉體是由一個平面圖形繞這平面內一條直線旋轉一周而成的立體，這條直線叫旋轉軸。由［1］知，當平面圖形是由連續曲線y=f(x)、直線x=a、x=b及x軸所圍成的曲邊梯形，而旋轉軸為 x軸時，所得旋轉體的體積為 V =f (x)]2dx;當平面圖形是由連續曲線x=φ(y)、直線y=c、y=d及y軸所圍成的曲邊梯形，而旋轉軸為y軸時，所得旋轉體的體積為V= φ (y)]2dy。下面討論:

命題1:當平面圖形是由連續曲線y=f(x)、直線x=a、x=b及x軸所圍成的曲邊梯形，而旋轉軸為y軸時，所得立體的體積為:Vy=.

命題2:當平面圖形是由連續曲線x=φ(y)、直線y=c、y=d及y軸所圍成的曲邊梯形，而旋轉軸為x軸時，所得立體的d體積為:Vx=.

2 命題證明

利用［1］證明命題1，如圖2－1

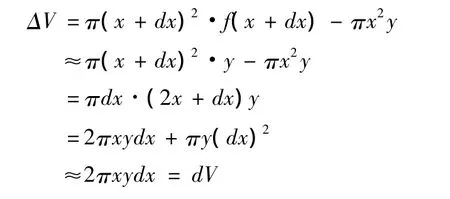
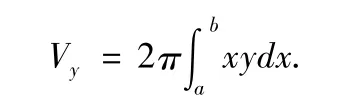
圖 2－1

命題2同理可證.

3 命題推廣

命題3:由連續曲線y=f(x)及y=g(x)圍成的封閉平面圖形繞y軸旋轉而得的立體體積為(如圖3－1):

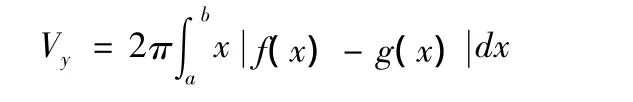
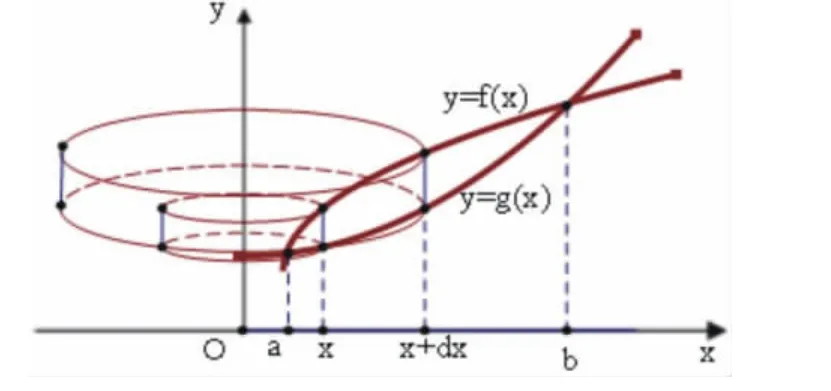
圖 3－1

命題4:由連續曲線x=φ(y)及x=ψ(y)圍成的封閉平面圖形繞x軸旋轉而得的立體體積為:

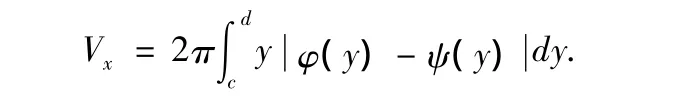
4 應用舉例

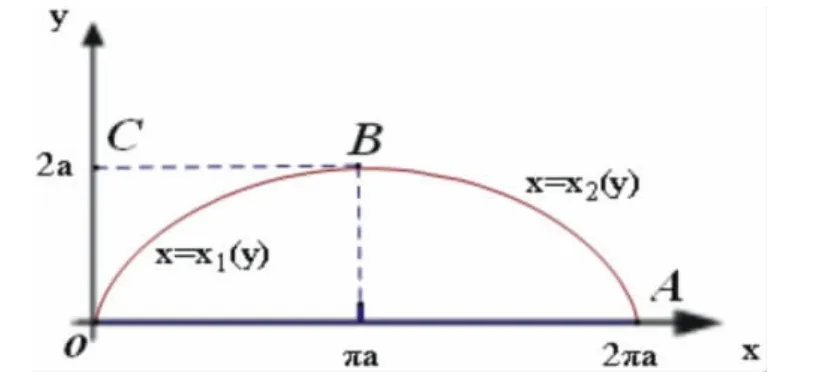
圖 4－1

解:方法一 利用［1］求出，如圖4－1.

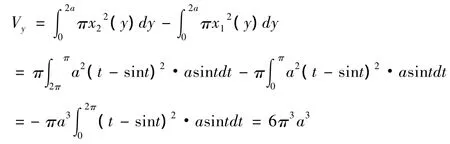
方法二 用柱殼法求出，如圖4－2.

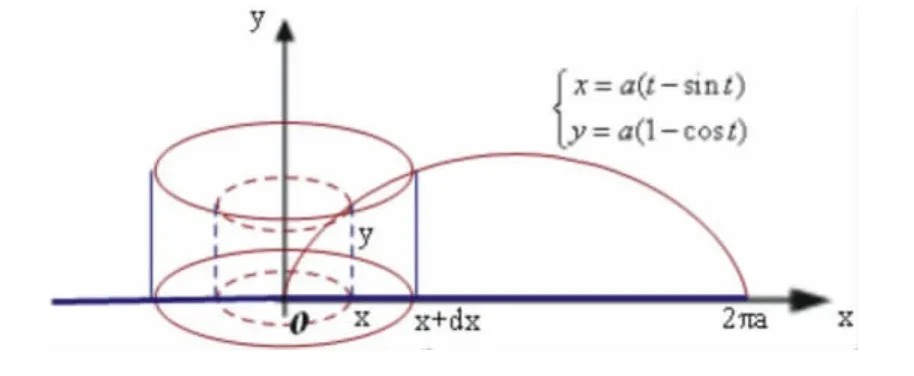
圖 4－2

柱面面積 2πx·y，柱殼體積 2πxy·dx.

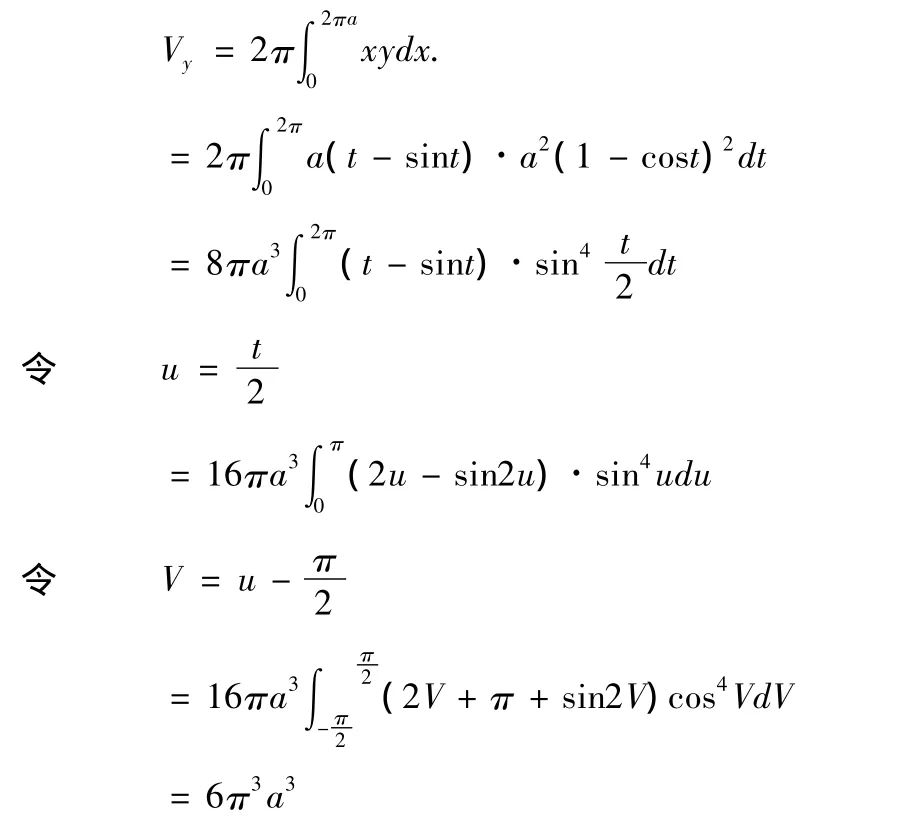
例2:求拋物線y=x2與直線y=x所圍成圖形繞x軸旋轉而得的立體體積.

解:方法一 利用［1］求出，如圖4－3.

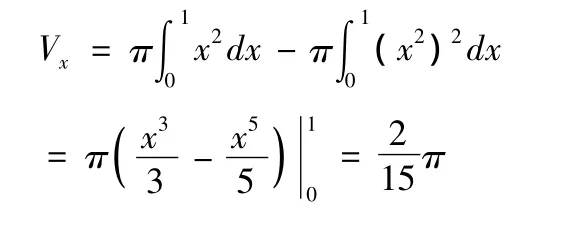
方法二 用柱殼法求出，如圖4－4.

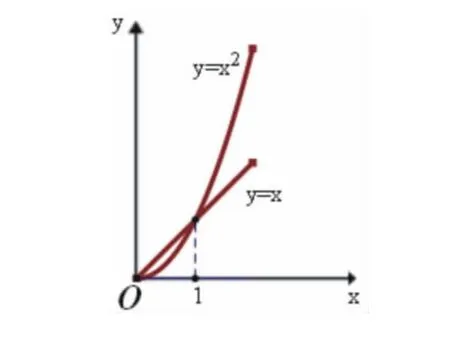
圖 4－3

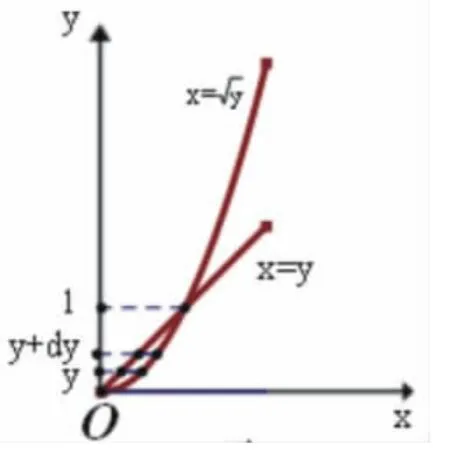
圖 4－4

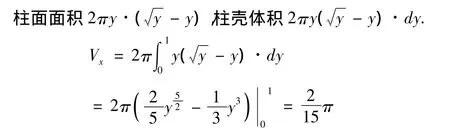
例3:設y=f(x)在x≥0時為連續的非負函數，且f(0)=0，V(t)表示y=f(x)，x=t(t＞0)及x軸所圍成圖形繞直線x=t旋轉一周所成旋轉體體積，證明:V'(t)=2πf(t).

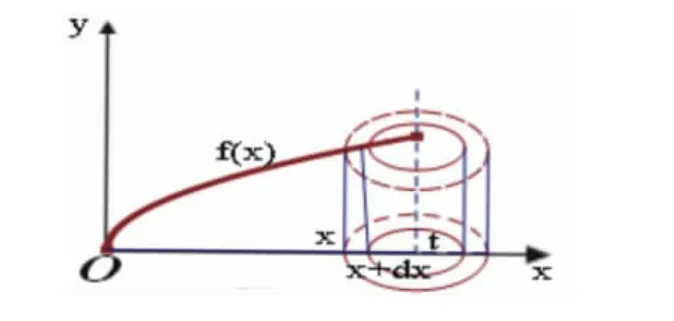
圖 4－5

證:利用柱殼法求出，如圖4－5.

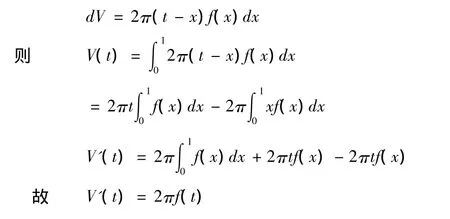
［1］同濟大學數學系.高等數學(上冊)［M］.第6版.北京:高等教育出版社，2007:278－280.