軌道交通荷載下飽和地基中波阻板主動隔振研究
高廣運, 王 非, 陳功奇, 張 博
(1.同濟大學地下建筑與工程系, 上海 200092;2.同濟大學巖土及地下工程教育部重點實驗室, 上海 200092;3.北京方興地產有限公司, 北京 100022)
引 言
近年來,多層的高架道路、地下鐵道、輕軌交通正日益形成一個立體空間交通體系。鐵路“十二五”規劃表明,中國將有30個左右的城市有發展城市軌道交通的可能,投入運營的城市軌道交通線路可能達到2 000~2 500 km。列車運行引起的振動對周圍環境的影響為成為人們關注的問題。
列車荷載引起的沿地面傳播的振動,可以采用不同隔振和減振措施。其中屏障隔振較為常見,高廣運將屏障分為兩類[1]:連續屏障(空溝、填充溝、鋼筋混凝土墻等)和非連續屏障(孔列、樁列和板樁等)。Woods在大量試驗的基礎上[2],提出有關屏障隔振設計的基本準則,并給出了衡量屏障隔振效果的參數——振幅衰減系數。
一種可供選擇的隔振措施是在振源或被保護結構下一定深度內埋置波阻板進行隔振。研究表明,基巖上單一土層的振動存在截止頻率,當地表作用的簡諧線荷載的頻率低于這個截止頻率時,土層中沒有波的傳播;僅當激振頻率大于截止頻率時,土層中才會出現波的傳播現象。根據土層中波的傳播存在截止頻率這個現象,Chouw等建議人工設置一個有限尺寸的人工基巖來進行隔振[3],并稱之為波阻板(簡寫為WIB)。Peplow等采用邊界積分方程法研究了二維雙層地基波阻板主動隔振的隔振效果[4]。Takemiya提出了采用蜂窩形柱狀波阻屏障(Honeycomb WIB)[5],對高架鐵路樁基振動Honeycomb WIB隔振進行了現場試驗,得到了令人滿意的隔振效果。李偉采用薄層法-邊界元建立三維層狀地基模型[6],分析了波阻板的隔振。高廣運和李寧等對波阻板進行了現場模型試驗[7],得出了一些有益的結論。
上述研究均假設土體為單相介質,忽略了孔隙水的影響,實際上孔隙水的存在對列車荷載作用下土體內波的傳播有很大影響。因此采用飽和多孔土體模型比線彈性模型更符合實際。高廣運等采用2.5維有限元法對飽和地基上列車運行引起的地面振動進行了分析[8]。徐斌采用積分方程法分析了飽和地基上移動荷載引起的排樁隔振效果[9]。
本文對列車-軌道子結構進行簡化計算,求得車輛對地基的激振力,對飽和土三維Biot波動方程進行積分變換,求解獲得飽和半空間表面位移的積分解答,最終得到飽和層狀地基的薄層法基本解答。同時運用旁軸近似原理,對飽和空間頻域-波數域內的剛度矩陣進行二階Taylor級數展開,獲得適應于薄層法底部邊界的旁軸近似解答。將軌道交通荷載作用下薄層法基本解作為格林函數,代入飽和土半解析邊界元中,編制相應的程序,針對飽和均質地基WIB隔振體系,詳細研究了影響隔振效果的主要參數(波阻板寬度、厚度、埋深和彈性模量),得到了軌道交通荷載作用下飽和地基WIB主動隔振的規律。
1 列車激振荷載的計算
軌道道床體系由鋼軌、軌枕、連接零件、道床、防爬設備及道渣等部件組成,直接承受由車輪傳來的巨大壓力,并將其傳遞給路基,故是十分復雜的系統。本文基于環境振動預測的需要,采用一種基于實測結果確定軌道交通荷載的方法,通過簡單的運算即可獲取列車通過軌道時的激振荷載。井上賸夫等在現場實測的基礎上提出了軌道激振力的合成方法[10],即通過對不同列車以不同車速通過無縫鋼軌時作用在道床上動力荷載的實測結果,得到以下主要結論:列車車輪對軌道產生的激振荷載主要由兩部分組成——隨列車移動的低頻豎向準靜荷載和車-軌共振產生的高頻動荷載。基于這兩部分動力荷載合成所得的作用在道床上的動力荷載與實測結果表明,二者在50 Hz以內十分接近。蔣通等同樣利用該法[11],對上海市軌道交通列車激振力進行計算,得到一些有益的結論。故本文采用文獻[10]的列車激振力的合成方法生成軌道交通的列車激振荷載。
根據文獻[10]可知單輪通過軌道時作用在道床上的激振力時程
P1(t)=P1msin(2πf1t)+P2msin(2πf2t)
(1)
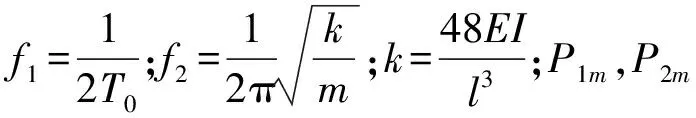
當n個輪子的列車通過軌道時,作用在道床上的激振荷載可以疊加求得。
設xi為第i個輪子與第一個輪子的距離,x1=0。則n個輪子的列車通過軌道時在激振點處作用在道床上的激振荷載為
(2)
式中P1(t)為式(1)所示單輪通過軌道時作用在道床上的激振力時程。
2 飽和地基的薄層法基本解答
薄層法屬于一種半解析半數值方法,即對波動微分方程在豎向進行與有限單元法(或采用其它數值逼近方法)類似的離散,將土層劃分為有限個薄層,而在其余坐標方向進行解析求解。
考慮簡諧運動(eiωt)的形式, 以孔壓和土骨架位移為基本量的Biot方程為
(3)
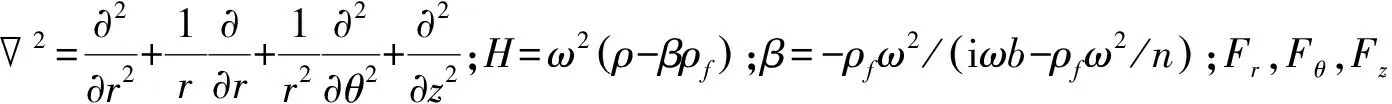
考慮水平面上的應力,并定義水平面上的“等效力”T={τrz,τθz,σz,qz}T,qz為孔隙流體的流量,故有
(4)
首先對豎向坐標z進行有限元離散,將半空間地基離散為ns個水平薄層。當每一層的厚度較小時,對于該層內的位移可采用線形插值模擬。假定沿薄層厚度方向的位移為二次分布,即對層內位移采用二次插值。第i層內的土體位移ur,uθ,uz,p為
(5)
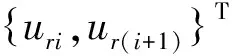
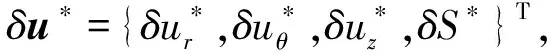
(6a)

(6b)
式(6)可以通過振型疊加法求解,得頻域波數域內力和位移的關系式。對給定的力P先進行切向坐標的Fourier分解,然后進行軸向坐標r的Hankel變換,可得頻域波數域內的位移表達式,再對該表達式進行Hankel逆變換和Fourier綜合,可求得頻域笛卡兒坐標系內的位移表達式,即薄層法的基本解。
以上推導和計算是在柱坐標系下進行的,根據坐標變換有
(7)
通過坐標變換即可求出直角坐標系下薄層法基本解。
對豎向坐標z進行的有限元離散,僅能將半空間離散為一定深度的有限個薄層,若這些薄層的總深度較小,則會產生較大的誤差。為了提高計算精度,且采用較少數量的離散結點,需要采取某些方法模擬底層半空間。旁軸近似是Kausel和Seale為解決薄層法模擬半空間的難題而提出的一種精度較高的措施[12],但僅給出了適用于彈性介質中底層半空間的旁軸近似解答。時剛等結合類似上述的推導[13],對飽和半空間波數域內的剛度矩陣進行二階Taylor級數展開,得到適合于薄層法的底層半空間的近似解答,提高了薄層法的計算效率。推導方法見文獻[13]。
3 飽和地基半解析邊界元法
研究飽和土地基的波動問題時,常規邊界元法一般采用全空間動力Green函數。因此,在進行邊界單元劃分時,不僅需要在結構-土體交界面上進行離散,還需要在半空間表面及不同土層的交界面上進行離散,從而大大增加了未知自由度的個數,導致計算時間和計算成本急劇增加,計算效率較低。為了減少未知量的個數,提高邊界元的計算效率,采用飽和半空間的位移、孔壓基本解答作為飽和土邊界元法的Green函數。這樣,在分析上述問題時,只需要在土與結構物的表面進行離散,而不需要在半空間表面和土層交界面上劃分單元,從而使邊界元法更好的適用于飽和半空間的情況。將飽和地基的薄層法基本解答與飽和土邊界元法結合起來,就構成了半解析邊界元法。所謂的半解析,就是指邊界元中采用的土骨架位移、孔壓、面力和流量的基本解是由薄層法所獲得的數值解答。
首先,將邊界Γ離散成E個單元,單元中任意點的位移、孔壓、面力和流量可以用單元節點對應量通過形函數來進行近似:
(8)
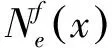
將式(8)代入邊界積分方程中,最終得到邊界元方程如下
(9)
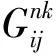
(10)
利用給定的邊界條件,即將給定的邊界節點上的位移、面力、孔壓和流量帶入上述方程組中,分離已知量與未知量及其相應的系數,得到可以求解的線性代數方程組,求解這個方程組即可得到所有邊界節點上的未知量。最后,可利用邊界單元的插值函數及各節點上的位移、面力、孔壓和流量來獲得邊界上任意點的對應量。
若飽和土的ρf→0和n→0時,則退化成彈性介質。因此可以采取退化的方法對飽和土半解析邊界元法進行驗證。為驗證薄層法基本解的正確性,這里選取Lamb問題進行對比分析[14]。王貽蓀利用突加力問題的閉合解求得了Lamb問題的精確解答[15]。針對Lamb問題,運用本文的算法與王貽蓀的解答進行了對比,如圖1示,計算結果較接近,因此驗證了本文的薄層算法。為了驗證半解析邊界元法的正確性,選取文獻[16]進行對比分析。Ahmad采用了常規邊界單元法求解出了均質地基中的三維空溝隔振問題[16]。從圖2中可以看出,兩者結果非常接近。
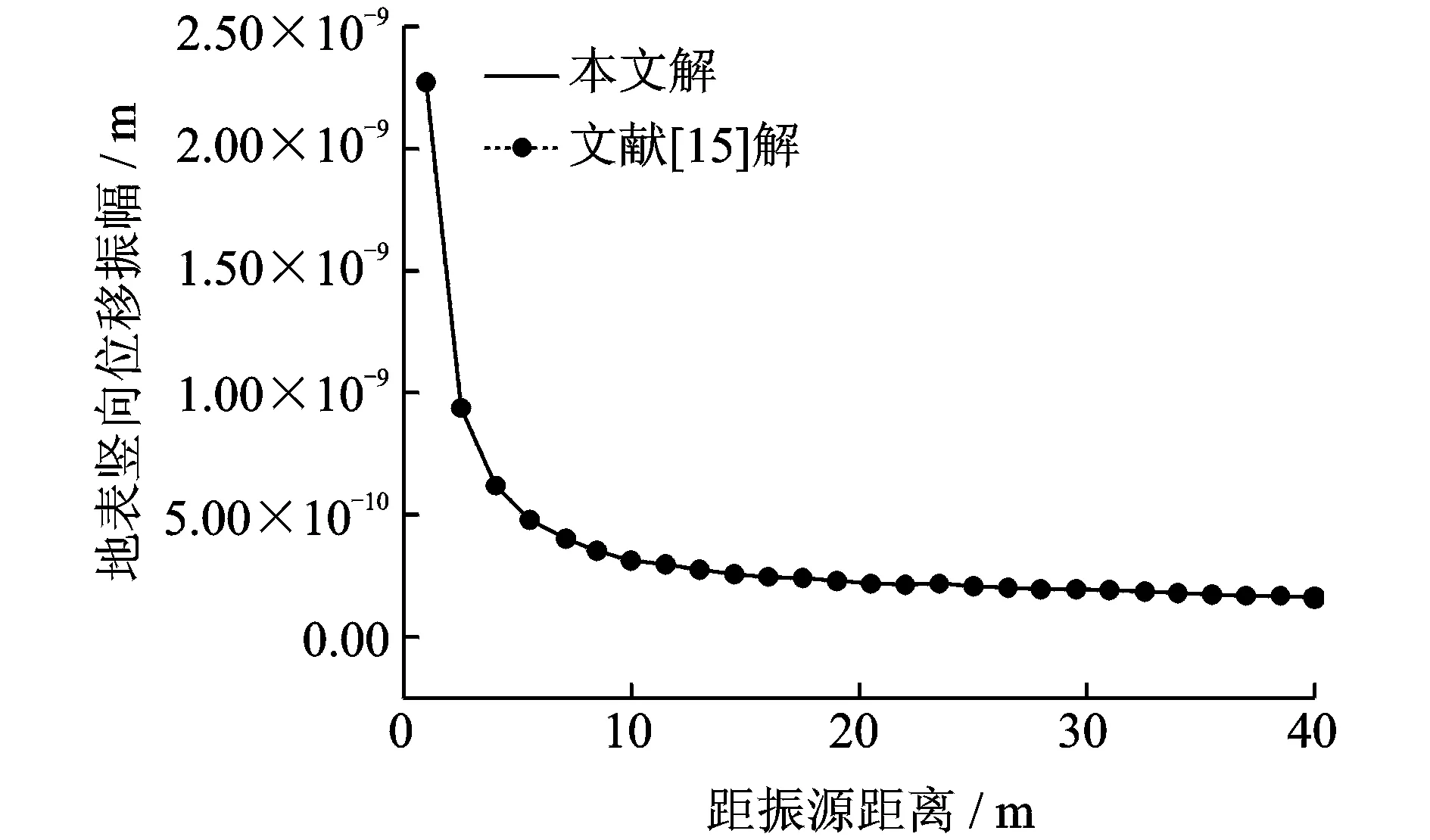
圖1 SH荷載激振地表位移解答對比
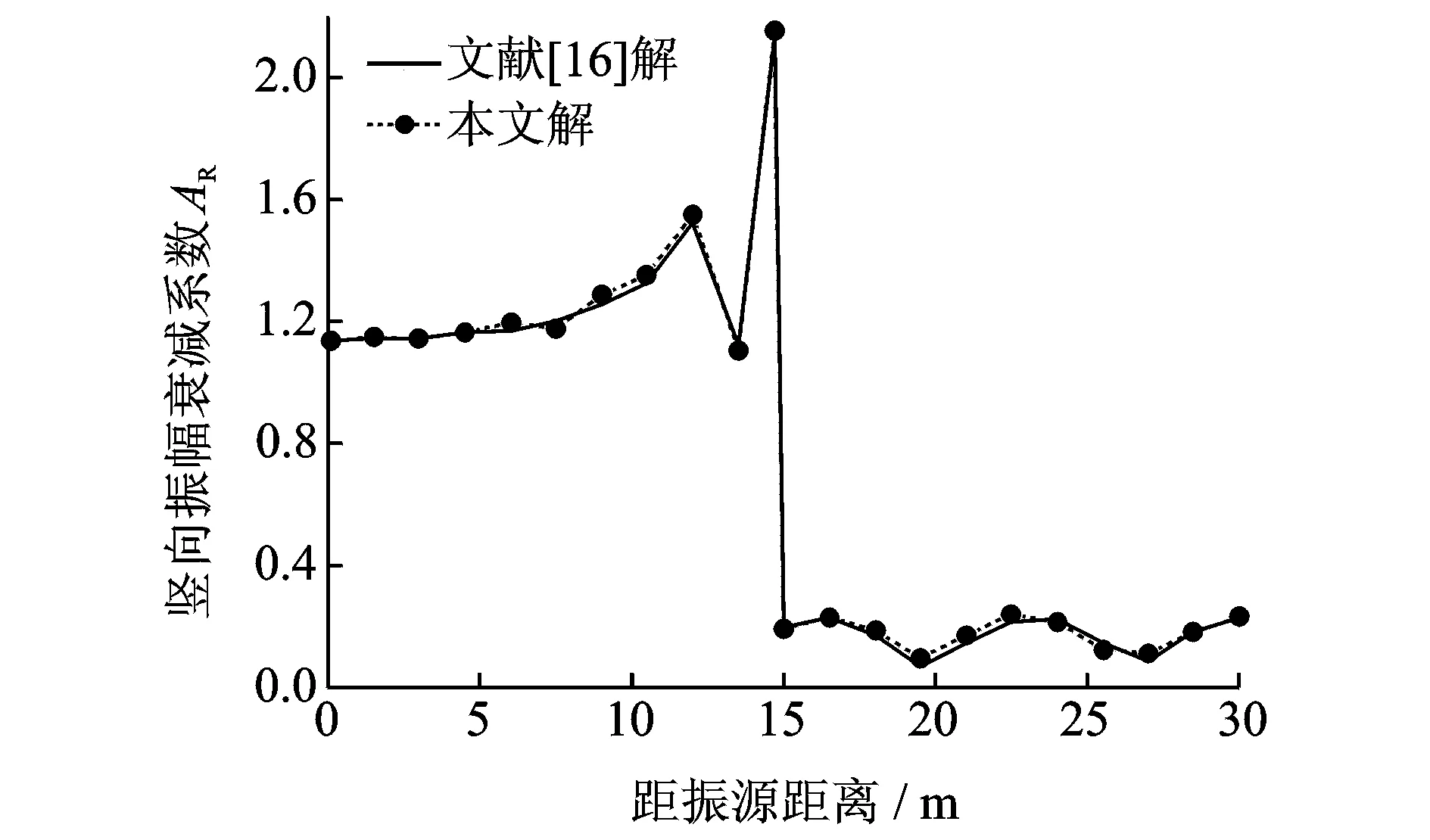
圖2 空溝隔振結果對比
4 列車荷載下飽和地基波阻板主動隔振分析
利用本文推導的結果,可以對軌道交通荷載作用下三維飽和地基中波阻板隔振效果進行分析。波阻板隔振計算模型如圖3所示。
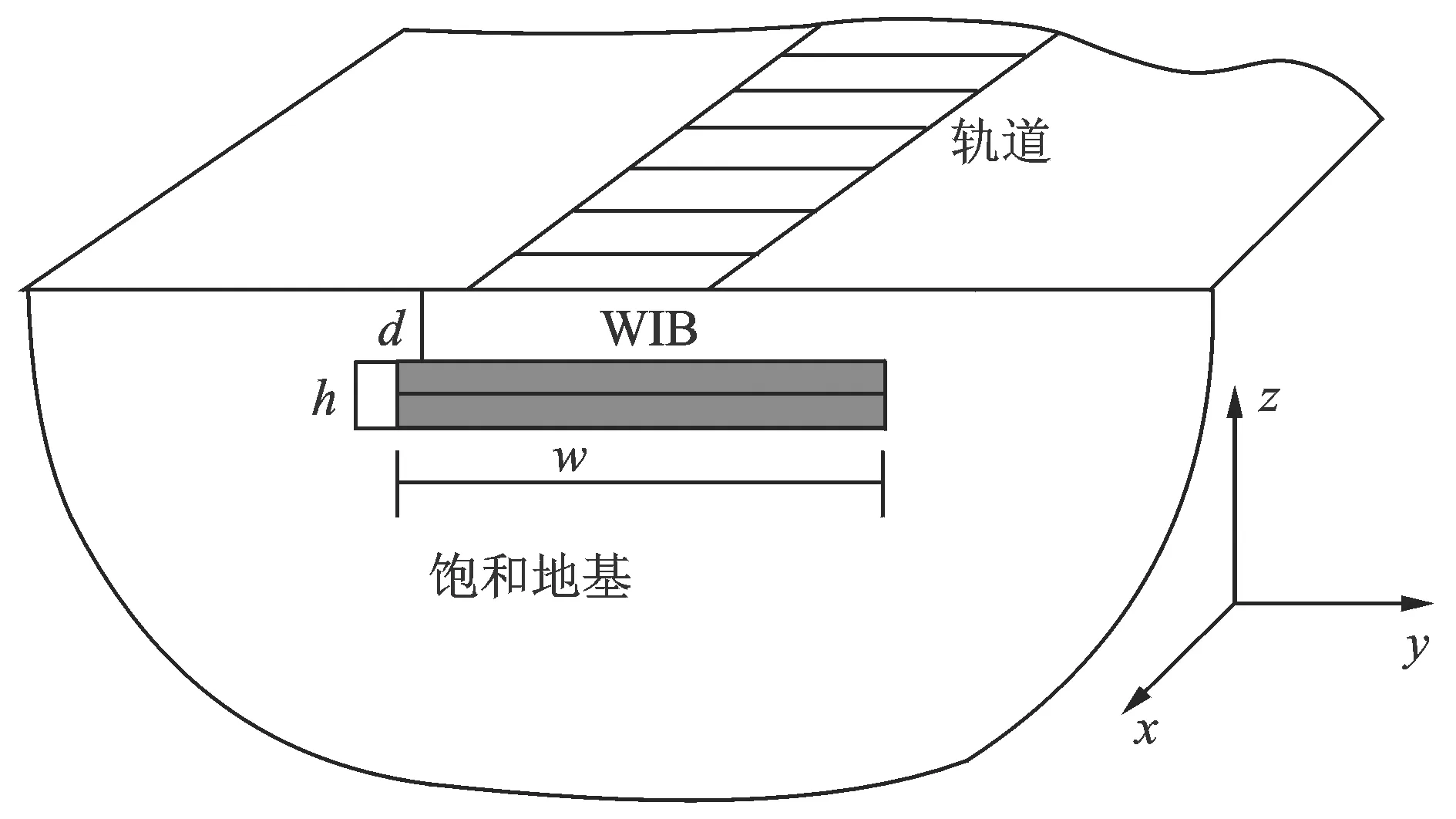
圖3 波阻板隔振示意圖
考慮上海市軌道交通列車通過軌道時對道床產生的激振荷載,每節車廂有2個輪對,各輪對質量為2 808 kg,空車質量為24 t,載重12.3 t(考慮定員的一半),車廂的長度為22.8 m,轉向架的間距為15.7 m,輪距為2.5 m,車速取60 km/h。軌道為60 kg/m的無縫鋼軌,取軌道結構計算寬度為3.0 m,鋼軌彈性模量取2.06×105MPa,軌道的彎曲剛度EI=6.627×106N·m2,將其代入式(2)即可得到列車激振荷載。飽和土體計算參數如下:土骨架密度為1 800 kg/m3,剪切波速為100 m/s,材料阻尼為0.05,泊松比為0.40,動力滲透系數為1×10-7m2,孔隙率為0.47,孔隙流體密度為1 000 kg/m3,流體體積模量為2×109Pa。假定下邊界為不透水基巖,則土骨架位移為零。考慮基礎為無質量的剛性基礎,WIB的寬度和厚度分別記為w,h;WIB頂面埋深為d,WIB的彈性模量記為E。WIB密度取ρb=2 000 kg/m3,泊松比取νb=0.20,WIB的粘滯阻尼比取ξb=0.05。
在分析某一模型參數時,其余參數則固定不變。用振幅衰減系數評價隔振效果[2]
(11)
4.1 WIB彈性模量對隔振效果的影響
圖4表示h=0.667B,w=6B,d=0.333B,B=3 m,為列車荷載作用寬度。WIB的彈性模量E變化時,地表水平向和豎向隔振效果隨距離的變化曲線。 由圖可知, 在軌道交通荷載作用下,豎向隔振效果略優于水平向隔振效果。隨著WIB彈性模量的增加,其隔振效果增加;即使當波阻板的彈性模量趨近于地基土的彈性模量時,其隔振效果也大于30%;當WIB的彈性模量E≥200 MPa時,豎向隔振效果可達50%以上。
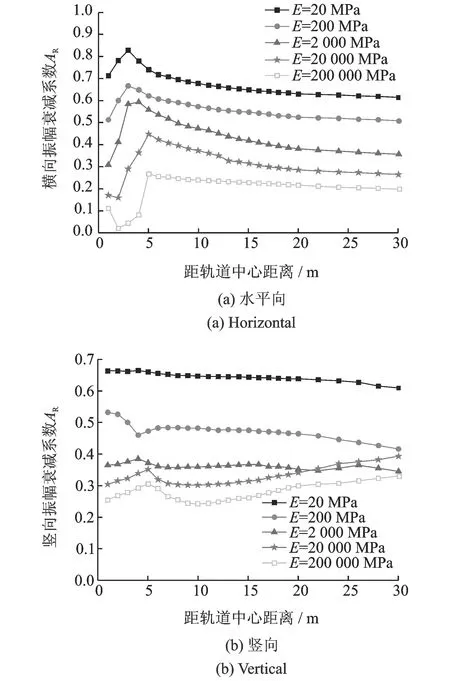
圖4 波阻板彈性模量對隔振效果的影響
4.2 WIB寬度對隔振效果的影響
圖5表示h=0.667B,d=0.333B,E=20 000 MPa,WIB的寬度w變化時,地表水平向和豎向隔振效果隨距離的變化。由圖可知,飽和地基采用WIB可取得理想的隔振效果。在軌道交通荷載作用下,豎向隔振效果略優于水平向隔振效果。如圖示,水平向隨WIB寬度的增加隔振效果增大;豎向的隔振效果略為復雜,當WIB的寬度較小(w≤6B)時,隨WIB寬度的增加,隔振效果增大,當WIB的寬度較大(w=9B和12B)時,隔振效果反而小于w=6B的工況,距軌道中心15 m外又小于w=4B的工況,但是總體來說,隔振效果均可達50%以上。
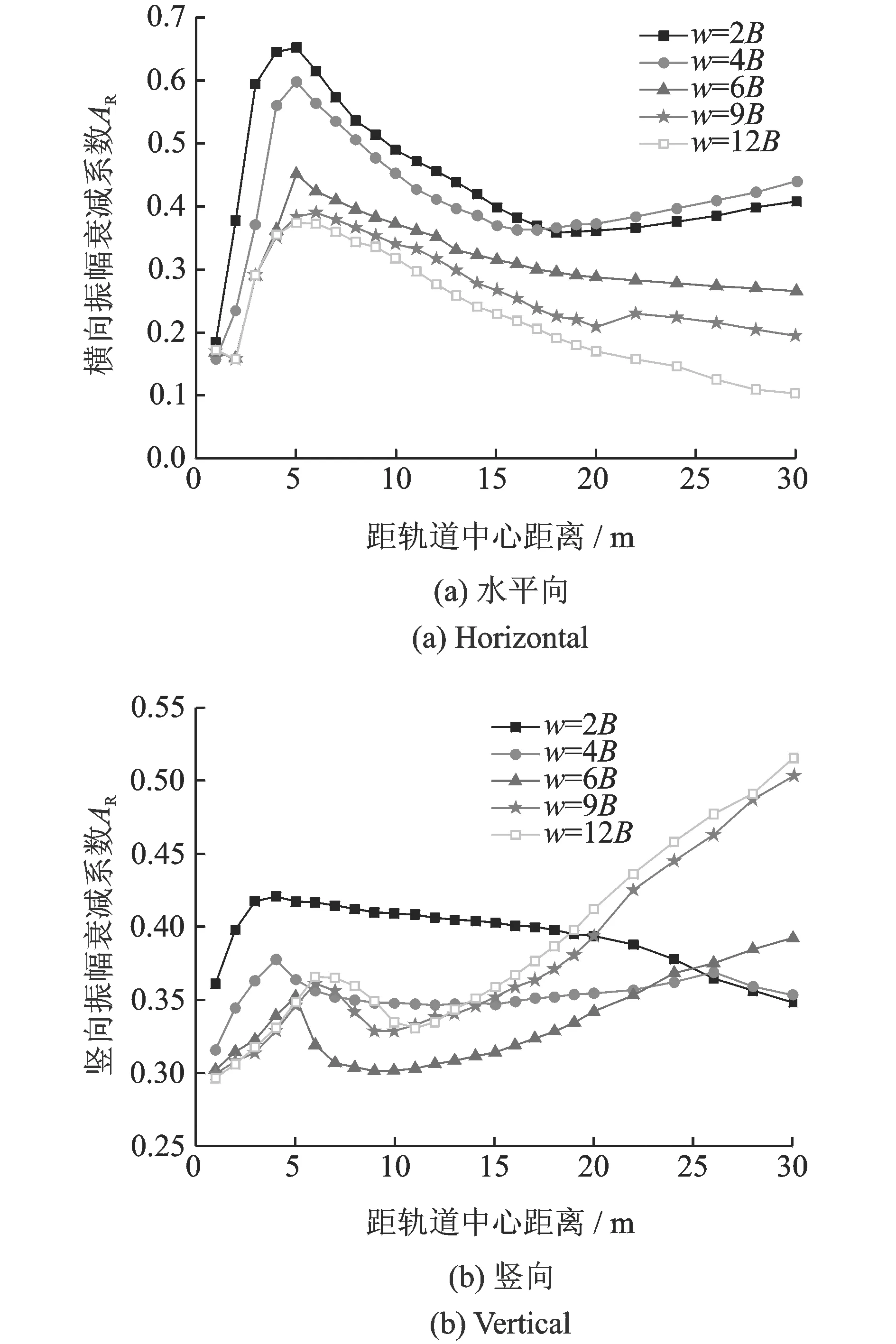
圖5 波阻板寬度對隔振效果的影響
4.3 WIB厚度對隔振效果的影響
圖6為w=6B,d=0.333B,E=20 000 MPa,WIB的厚度h變化時,地表水平向和豎向隔振效果隨距離的變化。由圖可知,在軌道交通荷載作用下,隨著WIB厚度的增加,隔振效果明顯增加;當WIB的厚度較小(h=0.333B)時,水平向和豎向位移隔振效果分別達40%和45%;當h≥0.667B時,豎向隔振效果增幅明顯減小,而水平向仍保持好的增幅。
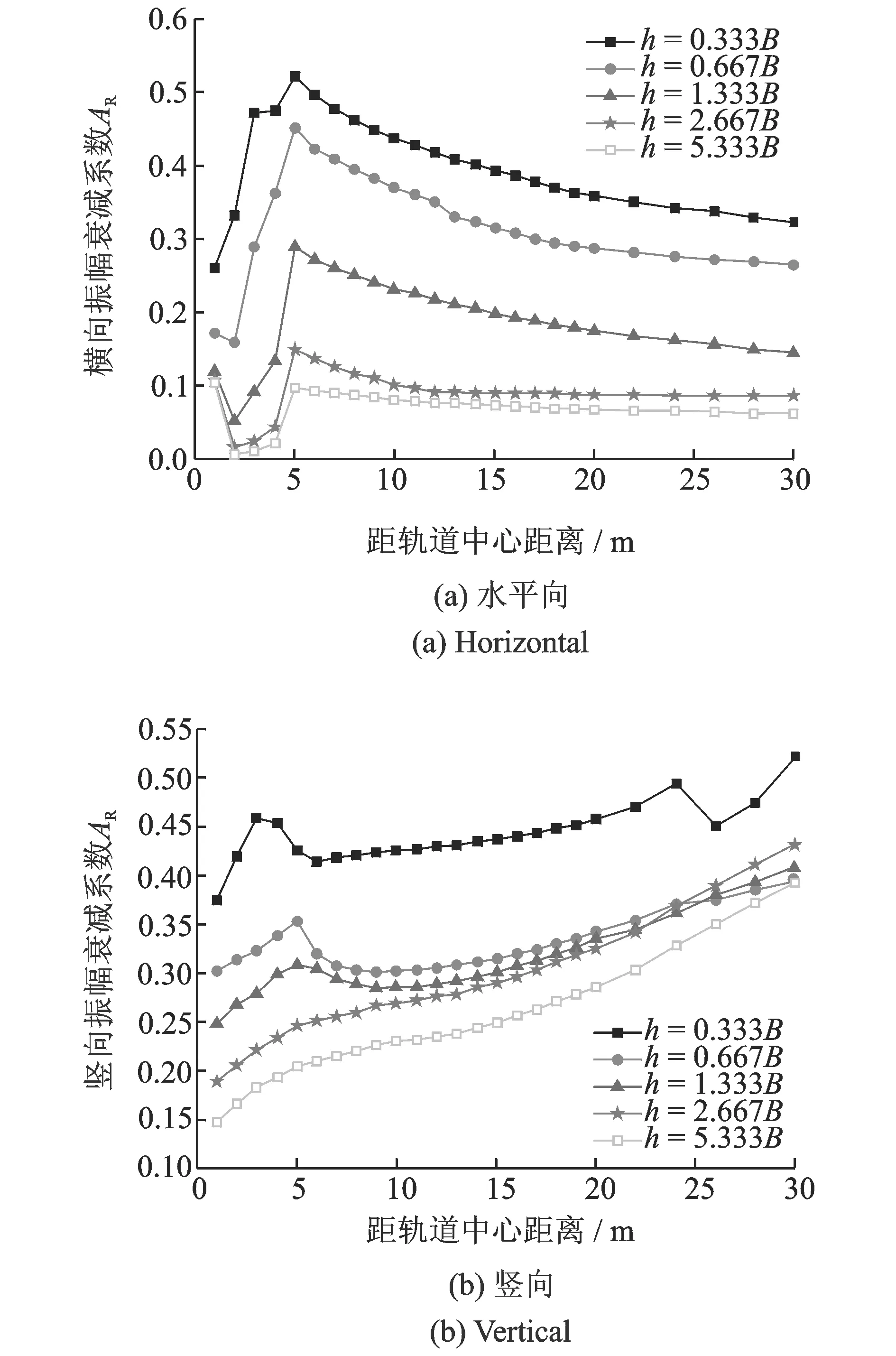
圖6 波阻板厚度對隔振效果的影響
4.4 WIB埋深對隔振效果的影響
圖7為h=0.667B,w=6B,E=20 000 MPa,WIB的埋深d變化時,地表水平向和豎向隔振效果隨距離的變化。由圖可知,在軌道交通荷載作用下,隨WIB埋深的增加,其隔振效果逐漸變差。當WIB的埋深較小(d≤0.667B)時,水平向和豎向隔振效果均可達60%,當WIB的埋深為0.667B 圖7 波阻板埋深對隔振效果的影響 本文首先建立了列車-軌道子結構進行了簡化計算,得到了列車的激振荷載,在飽和土頻域半解析邊界元法的基礎上詳細分析了軌道交通荷載作用下飽和地基WIB隔振體系的主動隔振效果,研究了參數變化時WIB的隔振性狀,結論如下: (1)利用薄層法基本解答建立的半解析邊界單元法,是分析土與結構動力相互作用的一種有效方法。在求解飽和三維地基中WIB隔振問題時,只需在土與WIB交界面進行離散,與常規邊界元法和有限元法相比,可以大大提高計算效率。 (2)增加WIB彈性模量和厚度均可增大其隔振效果。計算表明當WIB的彈性模量和厚度較小時,WIB也會達到理想的隔振效果。 (3)隨WIB寬度的增加,隔振效果增大;豎向隔振效果較復雜,設計時應充分考慮。分析表明,即使WIB寬度取小值時,隔振效果也可達50%以上。 (4)WIB埋深越小,隔振效果越好。計算表明當WIB的埋深較小時,水平向和豎向隔振效果均可達60%,當WIB的埋深變大時,隔振效果稍差。 參考文獻: [1] 高廣運.非連續屏障地面隔振理論與應用[D].杭州:浙江大學,1998.Gao Guang-yun. Theory and application of ground vibration isolation by discontinuous barriers[D]. Hangzhou: Zhejiang University, 1988. [2] Woods R D. Screening of surface waves in soils[J]. Journal of the Soil Mechanics and Foundations Division, ASCE,1968,94(4):951—979. [3] Schmid G, Chouw N, Le R. Shielding of structures from soil vibrations[J]. Proceedings of Soil Dyn. and Earth. Eng. V, Computational Mechanics Publications,1992:651—662. [4] Peplow A T, Jones C J C, Petyt M. Surface vibration propagation over a layered elastic half-space with an inclusion[J]. Applied Acoustics, 1999,56:283—296. [5] Takemiya H. Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct[J]. Soil Dyn. Earth. Engin., 2004,24:69—87. [6] 高廣運,馮世進,李偉,等.三維層狀地基豎向激振波阻板主動隔振分析[J].巖土工程學報,2007,29(4):471—476.Gao Guang-yun, Feng Shi-jin, Li Wei, Zheng Jian-guo. 3D analysis of active vibration isolation with wave impeding block in layered ground under vertical loading[J]. Chinese Journal of Geotechnical Engineering, 2007,29(4):471—476. [7] Gao G Y, Li N, Yue Z Q. Experimental study on active vibration isolation by WIB in layered ground under vertical loading[A]. 4th Int. Symposium on Environmental Vibration: Prediction, Monitoring and Evaluation[C]. Beijing, China. Beijing: Science Press, Xia and Takemiya (ed.) 2009:245—253. [8] 高廣運,何俊峰,楊成斌,等.2.5維有限元分析飽和地基列車運行引起的地面振動[J].巖土工程學報,2011,33(2):234—241.Gao Guang-yun, He Jun-feng, Yang Cheng-bin, et al. Ground vibration induced by trains moving on saturated ground using 2.5D FEM[J]. Chinese Journal of Geotechnical Engineering, 2011,33(2):234—241. [9] 徐斌.移動荷載引起飽和土動力響應及排樁隔振研究[D].上海:上海交通大學,2009.Xu Bin. A moving loads and analysis of vibration isolation effectiveness with pile rows[D]. Shanghai: Shanghai Jiao Tong University, 2009. [10] 井上勝夫,木村翔,北村訓久. 軌道上建築物に対する固體音制御のための列車走行時の加振力特性に関する研究[A]. 日本建築學會計畫系論文集[C].1992,432:11—20. [11] 蔣通,田治見宏.地基-結構動力相互作用分析方法—薄層法原理及應用[M].上海:同濟大學出版社,2009.Jiang Tong, TAJIMI Hiroshi. Soil-structure Dynamic Interaction Method: Principle and Application of Thin Layered Method[M]. Shanghai: Tongji Press,2009. [12] Kausel E, Seale S H. Dynamic and static impedances of cross-anisotropic halfspaces[J]. Soil Dyn. Earthq. Engrg., 1990,9(4):172—178. [13] 時剛,高廣運,馮世進.飽和層狀地基的薄層法基本解及其旁軸邊界[J].巖土工程學報,2010,32(5):664—671.Shi Gang, Gao Guang-yun, Feng Shi-jin. Basic solution of saturated layered ground by thin layered method and its paraxial boundary[J]. Chinese Journal of Geotechnical Engineering, 2010,32(5):664—671. [14] Lamb H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society, London (SerA), 1904,203:1—42. [15] 王貽蓀.地面波動分析若干問題[J].建筑結構學報,1982,4(2):16—17.Wang Yi-sun. Some issues about analysis of ground surface wave-motion[J]. Journal of Building Structures, 1982,4(2):56—67. [16] Ahmad S, Al-Hussaini T M. Simplified design for vibration screening by open and in-filled trenches[J]. Journal of Geotechnical Engineering Division, ASCE, 1991,117:67—88.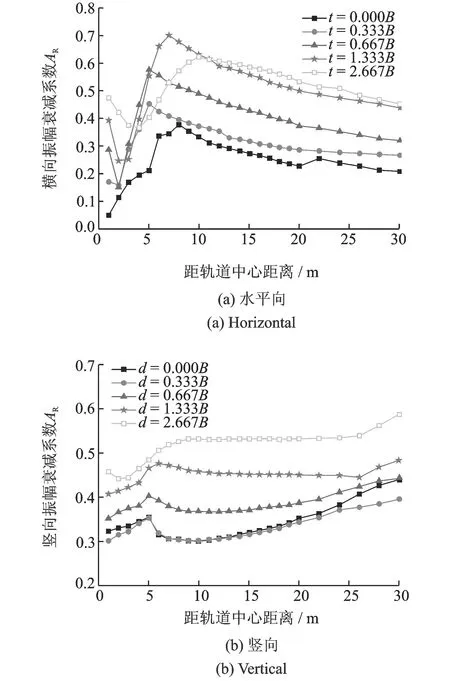
5 結 論

