基于DV-hop定位的誤差加權改進算法

(太原理工大學信息工程學院,山西 太原 030024)

0 引言

無線傳感器網絡(wireless sensor network，WSN)是部署大量低廉的智能傳感器節點，并以自組織、多跳方式構成的無線網絡系統。在傳感器監測區域內,傳感器將采集的數據進行傳輸和處理，實現對該目標區域的監測。無線傳感器網絡(WSN)具有無線自組織、高容錯性、動態性強的特點，被廣泛應用于軍事、環境監測、農業生產、醫療衛生等領域[1-2]。節點定位是網絡重構、檢測和定位必不可少的研究基礎。

按照是否要測量傳感器節點之間的距離，現有的傳感器定位算法可分為基于測距算法(range-based)和距離無關定位算法(range-free)兩類[3]。距離相關的定位是指網絡錨節點具有測量自身到鄰居節點的距離、信號的角度和強度的能力，然后通過三邊測量法、極大似然估計法等算法得出未知節點的坐標。傳感器距離定位包括到達時間法(time of arrival, TOA)、到達角度法(angle-of-arrival,AOA)、到達時間差法(time difference of arrival,TDOA)和接收信號強度指示法(received signal strength indication,RSSI)等方法。這些方法定位精度較高，但對硬件的要求高。距離無關的定位是通過節點間相互網絡連通度和通信半徑等，利用三邊測量法、極大似然估計法等算法得出未知節點的坐標。定位方法包括質心算法、APIT算法、DV-hop算法[4]等。距離無關定位算法不需要測量距離或角度的硬件，能耗較低，應用前景廣泛。

1 DV-hop算法

1.1 DV-hop算法流程

DV-hop算法是由Niculescu等學者提出的免于測距的算法，它的算法定位過程分為以下3個階段。

① 計算未知節點與每個錨節點的最小跳數

錨節點通過向傳感器網絡的鄰居節點發送自身的信息分組，每個節點維護1個數據表{i,(xi,yi),hi}。其中，(xi,yi)為結點i的二維坐標，hi為起始節點到節點i的跳數，初始化時設置為0。鄰居節點收到錨節點i的數據包后，將跳數hi加1，然后向鄰居節點廣播該數據包。接收節點保存每個錨節點的最小跳數，對于同一錨節點的較大的跳數則釋放。

② 校正值的計算和廣播

錨節點i記錄的信息包括其他錨節點j的坐標信息和跳數信息。所有錨節點的平均每跳距離Ci的計算式為：

(1)

式中：(xi,yi)、(xj,yj)分別為錨節點i和錨節點j的二維坐標；hij為兩錨節點之間的跳數距離。

將錨節點的平均每跳距離廣播至傳感器網絡中，未知節點僅接收第一個錨節點的每跳距離，并將其作為自身傳播的每跳距離，則可得出節點k與錨節點i的距離為Cik=Cihik。

③ 未知節點位置的計算

假設未知節點的二維坐標為(x,y)，錨節點i的坐標為(xi,yi)，而未知節點與網絡錨節點i的估算距離為di,則可得出以下公式：

(2)

設:

(3)

(4)

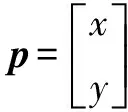
(5)

由最小二乘法,可得p=(ATA)-1ATB。

DV-hop算法在實際應用中存在以下不足。

① 算法中的每個節點要接收和轉發所有錨節點的數據包結構，這些節點處于活動狀態，需要較長時間等待數據包，網絡中的通信開銷和能量消耗隨之增加。

② 錨節點所占的比例不同，平均跳段距離也就不同。比例越高，平均跳段距離就越精確。當比例增加到一定程度時，距離保持穩定，但費用隨之增加。

根據試驗發現，未知節點與錨節點的估算距離影響了節點的定位精度。當未知節點與錨節點間距為一跳段時，測得的距離約為準確距離的1.2倍。隨著節點之間間距的增大，估算誤差也隨之增加。因此，使用全部錨節點反而降低了節點的定位精度。

1.2 粒子群算法在DV-hop中的應用

粒子群算法是對DV-hop算法中三邊測量法或最大似然估計法的未知節點坐標的誤差進行修正和優化，是非線性方程求解的有效解決方案。每個可行解相當于粒子群中的一個粒子，粒子通過個體最優解P和全局最優解G，利用式(6)更新下一個節點的個體最優解的位置和速度信息數據；然后在這個空間中改變位置和速度，向最優解靠攏。

(6)

式中：i為第i個粒子；t為粒子群的迭代次數；c1、c2為學習因子，以平衡局部搜索和全局搜索能力；xi為粒子i的位置信息。

粒子群初始化時要設置粒子位置信息的上下限xmax和xmin、粒子速度信息的上下限vmax和vmin、最大迭代次數[5-7]。

1.3 典型DV-hop改進算法

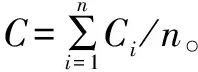
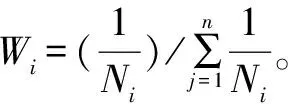
2 改進的DV-hop算法

本文對傳統的DV-hop算法進行了適當的改進。改進算法主要體現在以下3個方面：第一階段采用限定數據包的廣播范圍；第二階段采用了基于誤差修正加權和跳距估計算法；第三階段采用了基于粒子群的定位算法。粒子群算法通過不斷舍棄最遠節點而降低算法的復雜度。

DV-hop算法屬于無需測距的定位算法，硬件要求簡單，但網絡中錨節點與未知節點的排列方式并非成直線排列，所以節點之間跳數越多，估算平均每跳距離的誤差越大。改進的算法采用在錨節點向網絡中廣播的數據包結構中增加一個生存周期數據data，所以改進算法中的錨節點數據包中包括4個字段，分別為錨節點的標志i、錨節點的二維位置坐標(xi,yi)、跳數hi和data數據段。data數據表示錨節點能夠傳輸的最大傳播跳數，用于限定錨節點數據包傳輸的最大范圍。定位算法根據錨節點在無線傳感器網絡中的比例和網絡的規模來設置不同的data值。

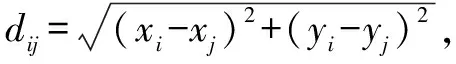
若網絡中總的錨節點數有M個，則錨節點i的平均每跳距離誤差值εi為：

(7)

某一錨節點i的距離誤差值越小，越能準確地估計出錨節點i的平均每跳距離。因此，誤差值越小，權值應該越大。

假設網絡中未知節點收到n個錨節點的數據報信息，錨節點i的平均每跳距離對應的加權值為：

(8)

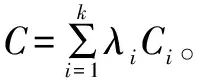
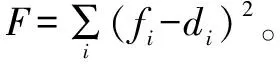
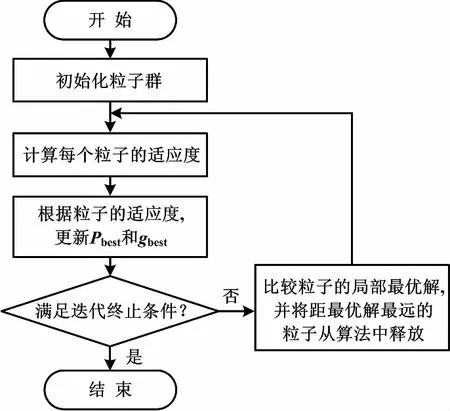
圖1 改進的粒子群優化算法流程圖

3 算法仿真及試驗分析

為了驗證本文所提改進算法在應用中的有效性和可行性，采用Matlab對本文提出的算法和DV-hop算法進行仿真和分析。試驗中將仿真節點隨機分布在二維平面上，在區域100 m×100 m 的范圍內隨機布置100個節點，仿真次數為200次。改進算法中的生存周期Hmax設置為6，學習因子c1=c2=2，粒子群的最大迭代次數為20。

平均定位誤差定義為：

(9)

歸一化的節點定位誤差定義為：

(10)

式中：xi,yi為節點i的估算距離；x,y為節點i的實際距離；R為節點通信半徑；m為網絡中的節點數，錨節點的個數按5、10、15、20、25、30、35、40依次增加。

3.1 錨節點對定位誤差的影響

仿真通過設置網絡中不同的錨節點數量，采用平均定位誤差對DV-hop算法和本文的算法進行比較。本文取網絡節點的數量為100，網絡節點通信半徑為20 m。在無線傳感器網絡中，錨節點的數量對節點的定位精度有一定的影響。當節點間通信半徑R=20 m時，不同的錨節點數量對DV-hop算法和本文算法的定位精度的比較如圖2所示。從圖2可以看出，隨著錨節點數的增加，兩種算法中節點能夠獲取的信息越多，節點獲得的定位距離信息越精確，定位精度呈現上升的趨勢。

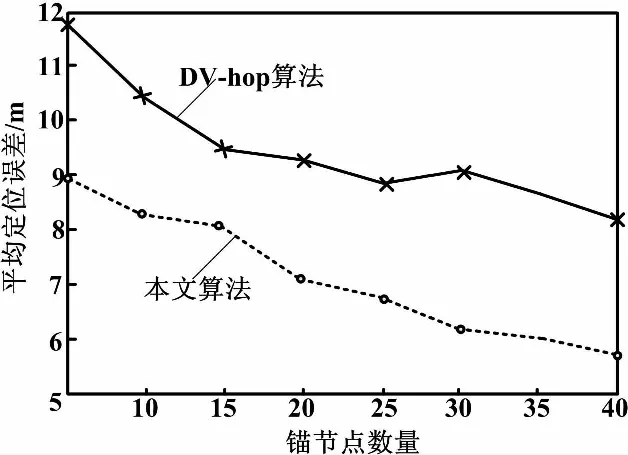
圖2 平均定位誤差曲線

當錨節點數增加到20時，本文提出的定位誤差有了明顯的改善；當錨節點數增加到30時，本文提出的算法相比于DV-hop算法,定位精度達到了3.4。從總體上來看，本文提出的算法比傳統的定位算法在定位精度上有了明顯的改善。

3.2 不同通信半徑對本文算法的影響

當錨節點按比例增加時，在節點間通信半徑為15 m、20 m、25 m、30 m這4種不同情況下，本文提出的改進算法的歸一化定位誤差的比較情況如圖3所示。從圖3可以看出，在4種不同通信半徑下，網絡的定位精度都隨著網絡中錨節點數的增加而更加精確。當錨節點達到一定比例時，定位精度趨于平穩。

圖3 歸一化平均定位誤差曲線

4 結束語

本文分析了DV-hop算法[10-14]的3個階段，闡述了兩種典型的改進算法，提出了基于DV-hop定位的誤差加權改進算法。

通過設定最大傳輸距離，減小了節點之間的傳播跳數，提高了未知節點的定位精度，降低了網絡的能耗開銷。同時對接收到的k個錨節點的平均每跳距離誤差加權和處理，使未知節點算出的平均每跳距離相比DV-hop更為準確，改善了無線傳感器網絡中的定位精度。改進的粒子群算法通過適應度函數減小了迭代的粒子數，縮短了不必要的迭代過程，從而有效改善了定位精度，減少了無線傳感器網絡定位的計算復雜度和計算時間，降低了定位誤差。仿真試驗驗證了本文提出的DV-hop定位改進算法的可行性。

[1] He T,Huang C D,Blum B M,et al.Range-free localization schemes in large scale sensor networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking.New York:ACM Press,2003:70-95.

[2] Cenedese A,Ortolan G,Bertinato M.Low-density wireless sensor networks for localization and tracking in critical environments[J].IEEE Transactions on Vehicular Technology,2010,59(6):2951-2962.

[3] 于弘毅，李鷗，張效義.無線傳感器網絡理論、技術與實現[M].北京：國防工業出版社,2008:143.

[4] Liu W Y,Wang E S,Chen Z J,et al.An improved DV-Hop localization algorithm based on selection of beacon nodes[J].Journal of Convergence Information Technology,2010,5(9):157-164.

[5] Kulkarni R V,Venayagamoorthy G k.Particle swarm optimization in wireless sensor networks:a brief survey[J].IEEE Transaction on Systems Man and Cybernetics,2011,41(2):262-267.

[6] Low K S,Nguyen H A,Guo H.A particle swarm optimization approach for the localization of a wireless sensor networks[C]//Proceedings of IEEE International Symposium on Industrial Electronic,2008:1820-1825.

[7] 黃艷，臧傳治，于海斌.基于改進粒子群優化的無線傳感器網絡定位算法[J].控制與決策，2012,27(1)：156-160.

[8] 朱紅松，孫利民.無線傳感器網絡技術發展現狀[J].中興通訊技術，2009,15(8):35-38.

[9] 肖美華，周之平.無線傳感器節點加權平均跳距定位算法[J].計算機工程與設計，2010,31(1)：78-81.

[10]劉凱，余君君，譚力雄.跳數加權DV-Hop定位算法[J].傳感技術學報，2012,25(11):1539-1542.

[11]趙林鎧,洪志全.基于無線傳感器網絡的DV-Hop定位算法的改進[J].計算機應用，2011,31(5):1189-1192.

[12]張愛平,賴欣.在JSP中調用JavaBean實現Web數據庫訪問[J].計算機時代,2007(1):15-18.

[13]仲偉和.基于JSP網頁自動生成工具的設計與實現[J].科技信息,2007(15):21-23.

[14]Lin C R, Gerla M.Adaptive clustering for mobile wireless networks[J].IEEE Journal on Selected Areas Communications, 1997,15 (7) :1265-1275.