FR共軛梯度法與泰勒級數展開法協同定位算法

(河北聯合大學電氣工程學院,河北 唐山 063009)

0 引言

在無線定位應用廣泛的今天，射頻識別(radio frequency identification,RFID)由于其非視距識別以及低成本的優點，被廣泛應用于室內定位。通過物理測量得到標簽與讀寫器之間的距離或角度的定位算法包括：到達時間法、到達時間差法、到達角法、接收信號強度法(received signal strength indication,RSSI)。在這四種方法中，到達時間法和RSSI比較常用。但由于到達時間法硬件要求太高，所以RFID定位系統中多采用RSSI[1]。

基于RSSI的無線射頻識別技術(RFID)是在已知發射功率的情況下，讀寫器測量接收功率，使用理論或經驗的信號傳播損耗轉化為距離。在獲得各個讀寫器到待測標簽的距離之后，根據標簽到各讀寫器的差值建立一組雙曲線方程。由于方程具有非線性，需要將其轉化為線性方程后求解[2]。在線性化方程的求解過程中，應用泰勒級數展開法，由于其具有很高的定位精度，在初始估計位置和實際位置相接近的情況下，可以得到較精確的定位結果；但在初始位置偏差較大的情況下，算法的收斂性難以保證[3]。為了確保定位結果的收斂性，本文采用FR共軛梯度法進行初始位置的計算[4]。

1 基于RSSI的定位算法

RSSI定位算法首先需要建立待測標簽環境的距離-損耗模型，然后設定已知讀寫器的參考位置。通過測量對比信號發射端與接收端的信號衰減情況來計算兩者之間的距離，設置多個讀寫器便可利用三邊或多邊定位法來完成對待測標簽的定位[5]。

電磁信號在室內空間傳播的過程中，會受到墻壁、障礙物等影響，產生能量損耗與衰減。這種因外界環境引起的衰減與電磁波發射與接收過程中所傳播的距離有直接的關系。RSSI采用的信號距離-損耗模型一般為對數距離衰減模型，其表達式為：

(1)

式中：d為發射機和接收機之間的距離；do為參考距離；η為信道衰減指數，一般取值2～4；Xσ為均值為零、均方差為σ的高斯隨機噪聲變量；P(do)為距離發射機do處的信號強度；P(d)為距離發射機d處的信號強度；P(do)可以通過經驗得出，通過信號強度P(d)求出距離d[6]。

如果四個讀寫器參與定位，則使用雙曲線模式建立方程組。根據對數距離衰減模型得到待定位標簽到各個讀寫器的距離后，可建立方程：

Di,1=Di-D1

(2)

(3)

如果三個讀寫器參與定位，則使用圓周模型建立方程：

(4)

式中：(Xi,Yi)為讀寫器坐標；(x，y)為待測標簽坐標；Ri為讀寫器與標簽之間的距離；N為參與定位的讀寫器數目。

式(2)的求解過程為求解非線性方程組，求解非線性方程組相當于無約束非線性最優化問題，非線性問題需要進行線性化處理[7]。

FR共軛梯度法是由線性問題發展而來的求解無約束非線性最優化問題的方法。其具有二次終止性，計算量小，因而得到廣泛應用。將FR共軛槽度法與泰勒級數展開算法相結合，可有效提高定位精度，保證定位的準確性[8]。

2 泰勒級數展開法

以下為四個讀寫器參與定位時，所建立的方程組通過泰勒級數展開法求解的過程。

根據式(2)定義函數：

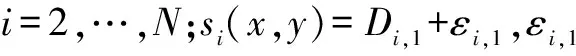
假設(x0,y0)為待定位標簽位置坐標的初始值：

x=x0+δxy=y0+δy

(5)

采用泰勒級數展開，僅保留前兩項可得：

(6)

(7)

式(6)可以寫為：

Aδ=D+e

(8)

令:

(9)

(10)

(11)

(12)

對于式(8)的加權最小二乘的解為:

δ=[ATR-1A]-1ATR-1D

(13)

令:

如果δz>10,則算法發散;如果δz<0.000 1,則算法收斂，停止計算，輸出定位結果。

3 FR共軛梯度法

首先將si(x,y)計算式改寫成：

ψi(x,y)=si(x,y)-di,1+εi,1i=2，…，N

(14)

使用FR共軛梯度法對式(14)構造模函數：

(15)

FR共軛梯度法將共軛性和最速下降方向相結合，利用已知迭代點處的梯度方向構造一組共軛方向，并沿此方向進行搜索，求出函數極小點。

設算法中所使用的各估計點為wk，對應的坐標為(xk,yk)，k=0，1，……。函數Ψ(x,y)在一點的梯度方向為G，-G即為最速下降方向[9]。在FR共軛梯度法中，第一個搜索方向取最速下降方向，即d0=-G0，其他搜索方向根據FR共軛梯度法得到：

dk+1=-Gk+1+βkdk

(16)

βk根據FR法計算，即：

(17)

設(x0,y0)為解的一個近似值，從此點開始進行搜索，搜索方向為最速下降方向，即d0=-G0。計算Φ在此點的梯度方向：

G0=(g10,g20)T

(18)

(19)

若‖G0‖<ε，則停止，w0為所求極小點；否則繼續計算。

若‖G0‖>ε，沿負梯度方向-G0跨一適當的步長λ0。步長的求取方法采用非精確線性搜索法Armijo準則，即：

(20)

式中：ξ∈(0,1)；σ∈(0,0.5)；gk為梯度方向；dk為搜索方向，令步長λk=ξmk，其中mk為滿足式(19)的最小非負整數。

搜索過程中，由m=0，mk=m開始搜索，wk+1=wk+ξmkdk，如果不等式成立，則停止運算；否則m=m+1，繼續運算。

求出的λ0可以使得新的點(x1,y1)為Ψ(x,y)在方向d0上的相對極小值，即：

Ψ(x1,y1)≈min{Ψ(x0-λ0g10,y0-λ0g20)}

(21)

將λ0代入下式：

wk+1=wk+λkdk

(22)

求得w1之后計算G1，若‖G1‖<ε，則停止，w1為所求極小點；否則重復上述過程，直到‖Gk‖足夠小為止。

4 改進算法仿真及分析

搜索過程中，首先使用FR共軛梯度法進行搜索定位。在位置比較接近之后，得到初步定位結果。然后使用Taylor級數展開算法對初步定位結果進行精確。

本文使用Matlab進行定位仿真[10]，仿真采用四個讀寫器，讀寫器的分布以及各個讀寫器大概的讀卡范圍如圖1所示。

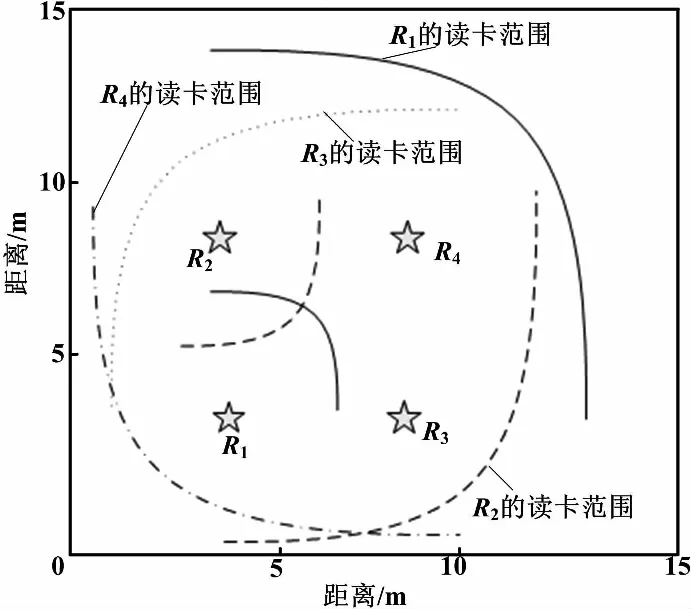
圖1 讀寫器分布圖

四個讀寫器的讀卡范圍分別為R1(5,5)，R2(5,10)，R3(10,5)，R4(10,10)。

每個讀寫器的識別距離在10 m以內，在仿真區域的中間部分，四個讀寫器均參加定位；在比較邊緣的位置，三個較近的讀寫器參與定位。

為了對比改進效果，本文對傳統泰勒級數展開法也做了仿真。仿真中協同定位算法和傳統泰勒級數展開法的仿真精度均取0.000 1。

根據所有仿真結果，當四個讀寫器均參加定位的情況下，定位結果受到初始值是否接近真實值，以及所得的測量值是否精確的影響。定位結果可以分為四類。

① 初始值接近真實值，所得的測量值精確，協同定位算法的結果與傳統泰勒級數展開法的結果相同。

② 初始值遠離真實值，所得的測量值精確，協同定位算法定位結果準確，且收斂情況良好，而傳統泰勒級數展開法則不能收斂。

③ 初始值遠離真實值，所得的測量值不精確，協同定位算法定位結果較為準確，且收斂情況良好，而傳統泰勒級數展開法則不能收斂。

④ 特殊情況為所得的測量值誤差較大，無論初始值是否接近真實值，協同定位算法與傳統泰勒級數展開法均不收斂，此時定位結果采用FR共軛梯度法的定位結果。

誤差采用均方根誤差RMSE:

(23)

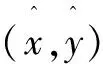
第二種情況，以真實點(6.3，7.9)為例，如表1所示，協同定位算法解決了傳統泰勒級數展開法不收斂的問題。

第四種情況，以真實點(3.3，6.9)為例，如表2所示，協同定位算法與傳統泰勒級數展開法均不收斂的問題，采用FR共軛梯度法的定位結果。

表1 初始值遠離時定位結果

表2 測量誤差較大時定位結果

定位結果分為以下兩類。

① 初始值接近真實值，協同定位算法比傳統泰勒級數展開法更加精確。

② 初始值遠離真實值，協同定位算法定位結果較為準確，且收斂情況良好，而傳統泰勒級數展開法則不能收斂。

以上兩種情況均以真實點(11.7，13)為例，一號讀寫器不參與定位。

第一種情況如表3所示，協同定位算法提高了傳統泰勒級數展開法的精度。第二種情況如表4所示，協同定位算法解決了傳統泰勒級數展開法不收斂的問題。

表3 初始值接近時定位結果

表4 初始值遠離時定位結果

5 結束語

分析仿真結果可得，FR共軛梯度法與泰勒級數展開法協同定位算法相結合，有效改進了傳統泰勒級數展開法在初始估計值距離真實值差距較大的情況下算法難以收斂的問題。當三個基站參與定位時，協同定位算法提高了定位精度。當三個基站參與定位、測量誤差較大的情況下，兩種算法均不收斂，可以采用FR共軛梯度法的定位結果，使得協同定位算法具有很強的應用性。

[1] 王保云.物聯網技術研究綜述[J].電子測量與儀器學報,2009(12):1-7.

[2] 徐加偉,牛清偉.淺談煤礦井下人員定位系統[J].煤礦開采，2009,14(4):72-74.

[3] 譚民,劉禹,曽雋芳.RFID技術系統工程及應用指南[M].北京:機械工業出版社,2007.

[4] 葉晨成,校景中,肖麗.基于RFID的井下人員定位系統[J].武漢理工大學學報：工學版,2010,32(15):146-149.

[5] 羊紅光,邢亞斌,張湃.基于RFID的井下人員定位系統[J].河北省科學院學報,2011,28(4):53-56.

[6] 劉宗元.基于射頻識別(RFID)的室內定位系統研究[D].中山：中山大學,2009.

[7] 李俊.基于RFID的室內定位系統的研究和設計[D].成都：電子科技大學,2009.

[8] 薛毅.最優化原理與方法[M].北京:北京工業大學出版社,2001.

[9] 林敏.RFID標簽定位技術研究[D].鎮江：江蘇大學,2007.

[10]樊榮.RFID讀寫器定位算法研究[D].成都：電子科技大學,2010.