時間窗下單船岸橋調度——基于數學規劃和規則的啟發式算法

樂美龍，趙彥營，劉秀玲

LE Meilong,ZHAO Yanying,LIU Xiuling

上海海事大學 物流研究中心，上海 201306

The Logistics Research Center,Shanghai Maritime University,Shanghai 201306,China

1 引言

隨著集裝箱運輸的不斷發展，集裝箱港口競爭日益激烈，為此，提高集裝箱港口生產率尤其重要。涉及集裝箱港口生產率的操作有兩項：岸橋、龍門吊的裝卸操作和集卡的水平運輸。其中，岸橋是集裝箱港口最重要也是最昂貴的設備。合理制定岸橋的調度計劃，有助于提高岸橋的生產率，減少船舶作業時間，降低港口運作成本，對提高集裝箱港口的競爭力具有重要意義。

岸橋問題分為兩種：岸橋安排問題QCAP（Quay Crane Assignment Problem）和岸橋調度問題QCSP（Quay Crane Scheduling Problem）。QCSP是指給已指定的一組岸橋進行裝卸排程。為此，必須定義裝卸任務屬性和岸橋屬性。

裝卸的任務屬性定義包括三個方面：

（1）任務的定義

①貝位域（Bay areas）：一個任務是由某些貝位上的裝卸集裝箱組成。

②單個貝位（Bays）：一個任務是一個貝位上的所有裝卸集裝箱。

③堆垛（Stacks）：同一貝位同一個列位置的一些集裝箱。

④集裝箱組（Groups）：同一貝位上的某幾個列上的集裝箱。它們通常有相同的目的地、類型等。

本文任務的定義：先根據貝位和裝卸操作分為一系列大任務，再將每個貝位上的有裝卸操作任務的一個集裝箱視為一個小任務，只有當岸橋出現替接移動時，才會出現大任務的分割。

（2）任務的優先順序：根據集裝箱在船上同一貝位的位置和裝還是卸操作而定。如一艘船舶：同一貝位先卸后裝；先卸甲板再卸艙內；先裝艙內再裝甲板。

（3）任務的不可同時執行性：由于岸橋的安全距離要求，有些任務不可以同時執行。

岸橋屬性定義包括六個因素：

（1）準備時間（Ready times）：每臺岸橋的最早可獲得時間。

（2）時間窗（Time windows）：每臺岸橋都有一個可作業的時間窗。

（3）位置（Position）：每臺岸橋都有一個初始位置和終止位置。

（4）轉移時間（Travel times）：每臺岸橋在貝位之間轉移的時間。

（5）安全距離（Safety margins）：同時作業的兩臺岸橋之間都有一個最小的安全距離，即8個貝位距離。

（6）岸橋的裝卸速度：由于岸橋或岸橋司機的操作熟練程度不一樣，每臺岸橋的裝卸速度也不一樣。

理論研究中主流的岸橋調度目標函數有兩個：一是最小化岸橋的最遲作業完成時間和所有岸橋作業時間總和，前者權重大于后者；二是最小化岸橋的最遲作業完成時間。

在岸橋調度研究方面，Dirk Steenken[1]等人建立了just-in-time調度模型，研究了出口集裝箱船的每個集裝箱的船上儲位問題，目的是減少岸橋的等待時間。Kim和Park[2]研究了單艘船舶的岸橋調度問題，在考慮岸橋任務的優先順序、岸橋之間的安全距離等因素下，建立混合整數線性模型，運用分支定界法和貪婪隨機自適應算法進行了求解。Luigi Moccia[3]等人在Kim和Park模型基礎上進一步拓展了約束條件的范圍，他們運用CPLEX和分支-切割算法來分別求解小、大規模岸橋問題。Young-Man Park[4]等人研究了在堆場龍門吊干擾下的岸橋調度問題，運用貪婪隨機自適應算法進行了求解。Marcello Sammarra[5]等人采用Kim和Park的模型，將岸橋調度問題分解為路徑和排程兩個子問題，從而轉化為求解最小化最長路徑問題，分別運用禁忌搜索算法和局部搜索算法進行求解。Der-HorngLee[6]等人在以一個船艙為一個任務、岸橋之間沒有相互干涉限制的條件下建立了混合整數線性模型，運用遺傳算法進行了求解。R.Tavakkoli-Moghaddam[7]等人拓展了Kim和Park的模型，從岸橋成本角度，通過建立混合整數線性規劃模型，研究了多條船舶的岸橋安排問題和岸橋調度問題QCSAP（Quay Crane Scheduling Assignment Problem），并運用 LINGO和一種有效的遺傳算法分別求解了小、大規模問題。Frank Meisel[8]等人研究了單向移動的岸橋調度問題，他們通過建立分割圖模型（Disjunctive graph model），運用分支定界啟發式算法進行求解，并提出了新的分支原則。Kap Hwan Kim[9]等人研究了雙吊具技術下的岸橋調度問題，它以最大的雙吊具岸橋的操作次數（也就是最小化岸橋的操作次數）為目標函數，運用一種混合啟發式算法進行求解。Der-Horng Lee[10]等人研究了關于進口集裝箱的岸橋和集卡聯合調度問題，通過建立混合整數線性模型，并運用遺傳算法和改正的規則啟發式算法（Modified Johnson’s Rule-based Heuristic Algorithm，MJRHA）進行了求解。Frank Meisel[11]建立了帶有時間窗的岸橋調度模型，并運用樹枝搜索啟發式算法進行了求解。Frank Meisel[12]等人研究了單艘船舶的岸橋調度問題，在不同工作效率、時間窗，并向同一個方向移動條件下，建立混合整數線性模型，運用分支定界法求解模型，并提出了新的分支原則。

在上述研究基礎上，綜合考慮岸橋屬性和任務屬性因素，提出了基于規則的、更貼近實際的、帶有時間窗的岸橋調度優化問題，并進行了分階段求解。

2 問題描述

在文獻[11-12]基礎上，給定一組岸橋，采用最小化單艘船舶岸橋最遲作業完成時間為目標函數；考慮任務屬性中任務的優先順序、不可同時執行性和岸橋屬性中岸橋的時間窗、轉移時間、初始位置、安全距離、裝卸速度等因素，通過建立混合整數線性模型P1，得出各臺岸橋的裝卸任務時序表。岸橋調度問題流程如圖1所示。

圖1 岸橋調度問題流程

模型基于以下假設：

（1）岸橋在同一軌道上作業，因此岸橋不能交叉作業；

（2）岸橋只能在可獲得的時間窗內作業；

（3）同時作業的兩臺岸橋之間都有一個最小的安全距離，即8個貝位距離；

（4）岸橋的裝卸速度：岸橋是同一性的。但由于港口每臺岸橋司機的操作熟練程度不一樣，岸橋的工作速度也不一樣。

3 數學模型P1

3.1 參數

3.2 決策變量

W ，船舶裝卸完成時間；Ci，任務i的完成時間；Ek，k岸橋的結束時間。

Zij，任務i和任務 j不能同時執行；任務i完成后，任務 j才能開始取1，反之0。

3.3 目標函數

目標函數式（1）表示單艘船舶的最小化作業完成時間。目標函數也可以表示為：

3.4 約束條件

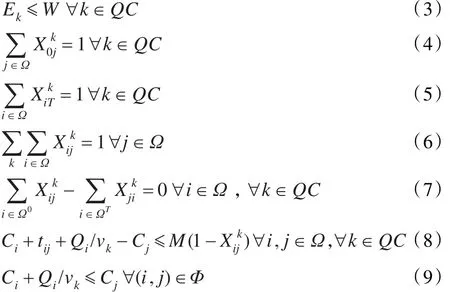
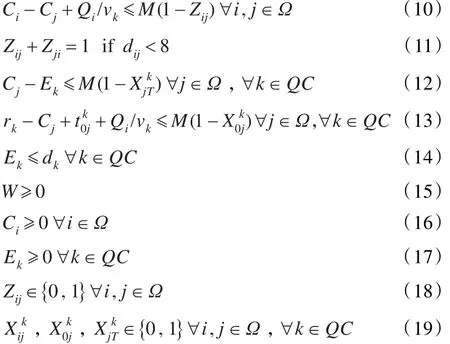
模型最終給出船舶的岸橋作業完成時間和帶時間窗的岸橋調度時序表，其中岸橋調度時序表包含了每臺岸橋的任務次序、每項任務的開始時間和結束時間。公式（3）表示船舶作業完成時間不早于任何一臺岸橋的最遲作業完成時間。公式（4）定義了每臺岸橋的第一項任務。公式（5）定義了每臺岸橋的最后一項任務。公式（6）定義了一項任務一次只能有一臺而且必須有一臺岸橋去執行。公式（7）表示岸橋執行任務的流動平衡，即每臺岸橋不管從哪個任務進入任務 j，就必須從任務 j轉入別的任務。公式（8）定義了每項任務的完成時間。公式（9）定義了有優先順序的集合對(i，j)，任務i必須在任務 j開始之前完成。公式（10）表示若任務i在任務 j之前，任務 j開始時間必須在任務i完成后。公式（11）定義了當任務i和任務 j距離小于8個貝位時，任務i和任務 j不能同時作業；要么任務i作業在前，任務 j作業在后；要么任務 j在前，任務i在后。公式（12）定義了每臺岸橋的完成時間。公式（13）和公式（14）定義了每臺岸橋可作業的時間窗。公式（15）～（17）定義了三個正數變量。公式（18）和公式（19）定義了四個0-1變量。

4 基于規則的啟發式算法

4.1 簡單模型P2

為降低上述模型P1的求解復雜度，在文獻[11-12]基礎上建立了簡單模型P2。P2只初步求解單艘船舶岸橋的最短作業完成時間，不求每臺岸橋的每項任務的開始時間和完成時間。

4.1.1 簡單模型P2問題描述

給定一組岸橋，考慮岸橋的時間窗、移動時間和裝卸速度三個因素，建立以單艘船舶岸橋的最短作業完成時間為目標函數的模型P2。基于下述假設，建立模型P2。

（1）岸橋之間不存在干擾，不考慮岸橋之間的安全距離。

（2）不考慮裝卸任務之間的優先關系。

（3）每臺岸橋都有可作業的時間窗。

（4）岸橋在兩個貝位間有一定的轉移時間。

4.1.2 簡單模型P2引入新的決策變量如下：

Dk1，如果k岸橋；0，否則。

簡單模型P2：

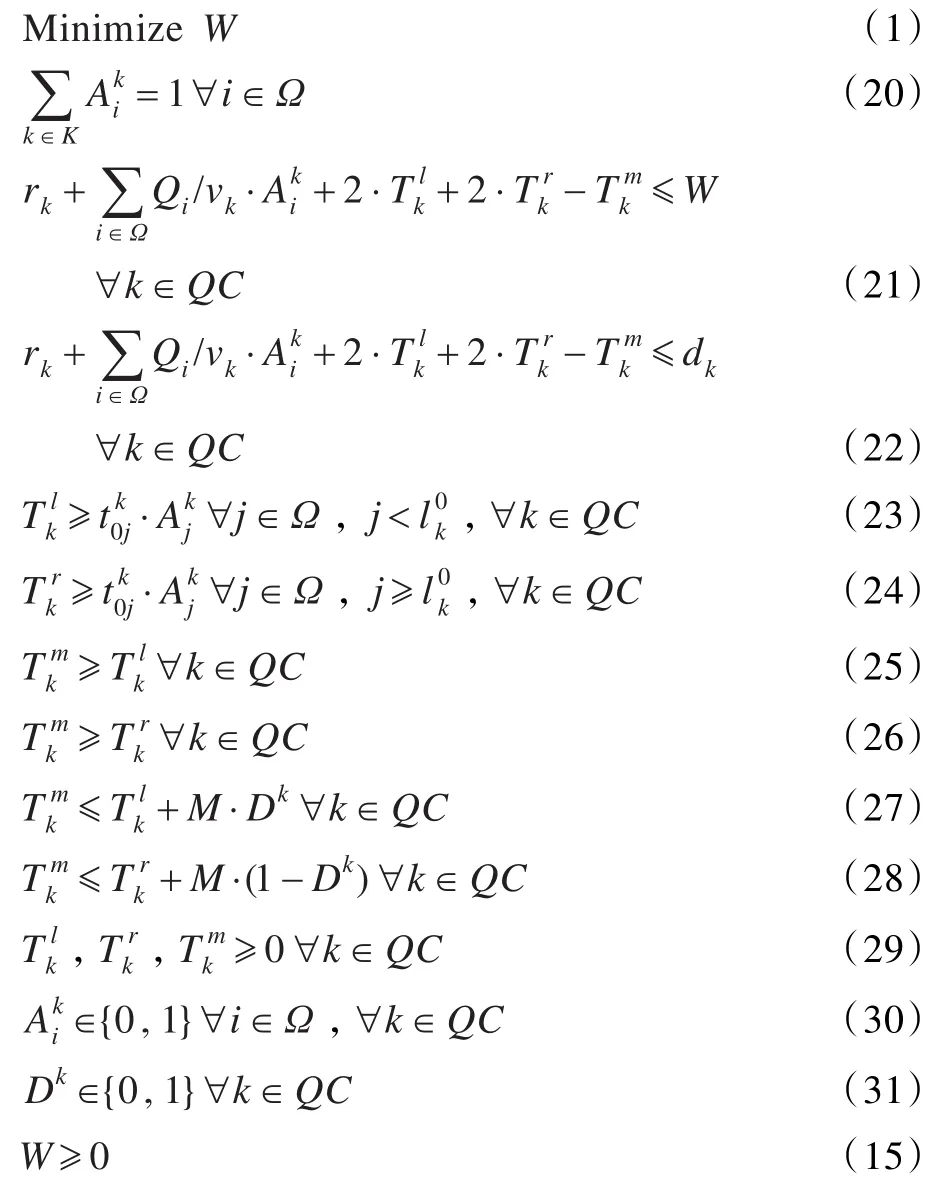
公式（1）仍是目標函數，表示單艘船舶的最短作業完成時間。公式（20）定義了船舶作業完成時間不早于任何一臺岸橋的最遲作業完成時間。公式（21）定義了每臺岸橋可作業的時間窗。公式（22）～（28）定義了每臺岸橋的最小移動時間。公式（29）定義了三個正數變量。公式（30）和公式（31）定義了兩個0-1變量。

4.2 基于規則的啟發式算法

在給定的岸橋時間窗下，為岸橋制定岸橋調度時序表，它是指給各岸橋分配船舶裝卸作業任務并安排作業先后順序。目標是使各岸橋結束作業必須在岸橋的時間窗內結束，并且船舶在港的作業時間最短。啟發式算法的主要思想：階段1，根據裝卸船基本原則構建模型初始值。階段2，在初始值基礎上，根據裝卸船基本原則和岸橋的具體工作時間進行局部調整，如果求得的解優于當前解，則更新當前解；否則，不斷迭代，直到得到滿意解。基于規則的啟發式算法流程圖如圖2所示。

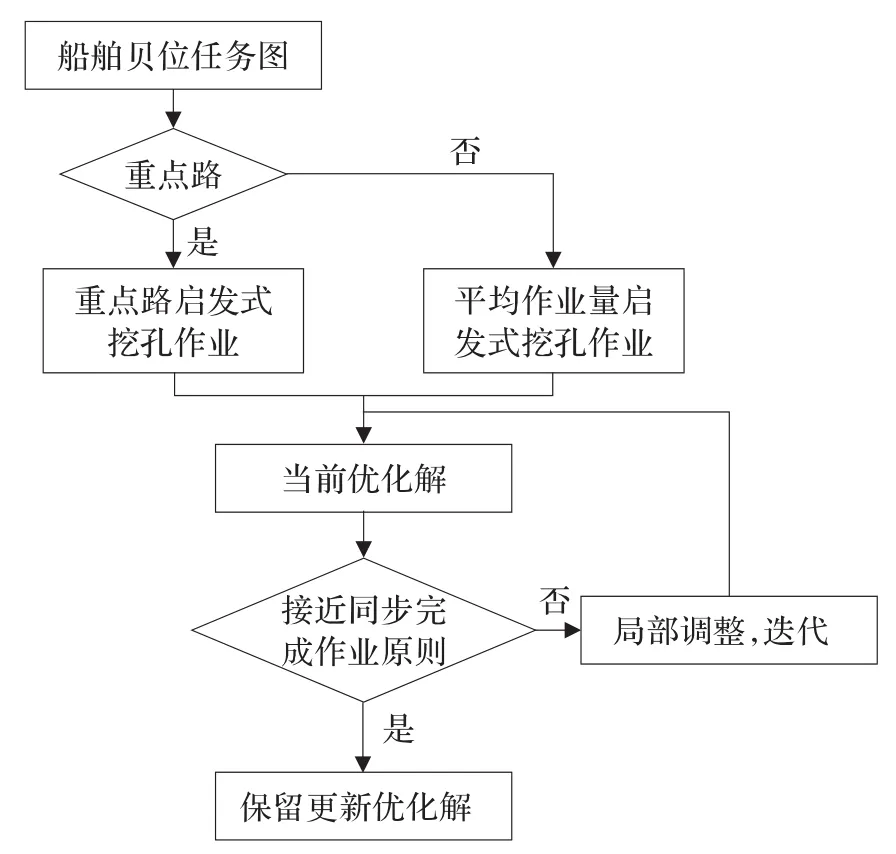
圖2 基于規則的啟發式算法流程圖

4.2.1 啟發式算法階段1

階段1根據裝卸船基本原則構建模型初始值。

裝卸船規則的優先級：

首先進行重點路的判斷。

（1）如果有重點路，保證重點路作業，保證不使次重點路人為變成重點路。

（2）如果沒有重點路，先做高柱貝位，避免產生重點路；盡量平衡各路作業量。

其次考慮挖孔作業，方便后來同時多路作業。

最后按照岸橋的移動方向完成整艘船舶作業。

步驟1根據船舶的貝位任務柱形圖3確認是否有重點路。

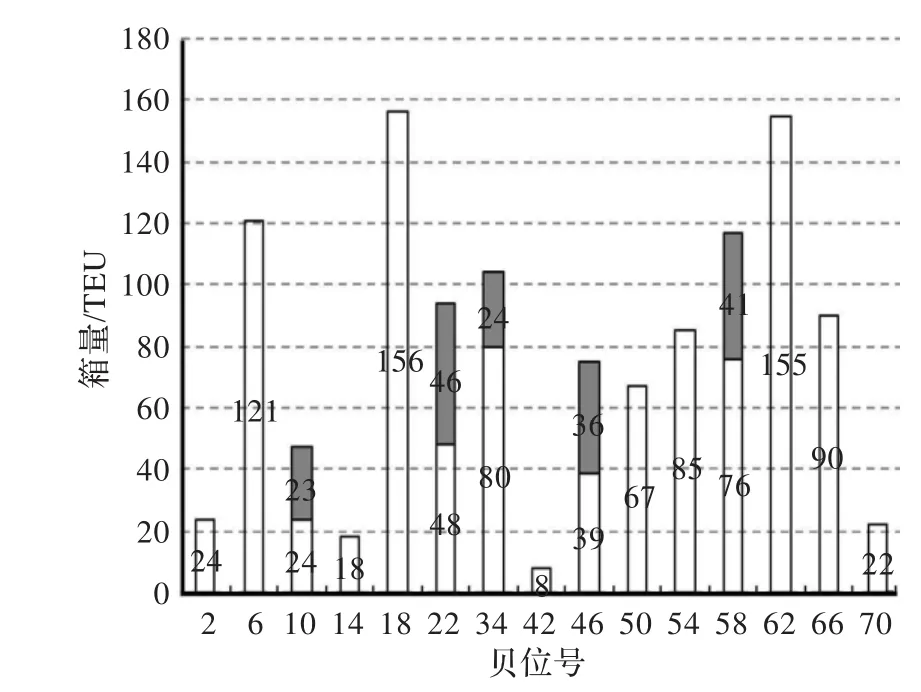
圖3 船舶貝位柱形集裝箱圖

重點路定義為：單船相鄰兩個大貝位上的任務箱量大于平均作業路數箱量。兩個大貝位（八個貝位）的最大箱量 Qz：當時，。平均作業路數箱量Qm=總作業量/作業路數，Qm=Q/m。當Qz≥Qm，此為重點路，進入步驟2和步驟3；當Qz＜Qm，此船無重點路，進入步驟2和步驟4。

根據船舶的貝位任務數量，即船舶的貝位任務柱形圖（見圖3），結合該船總的裝卸箱量，可確認該船舶是否有重點路。

步驟2挖孔作業思想

挖孔作業是指單船上連續三個大貝位都有裝卸任務時，安排岸橋先執行中間的一個貝位上的任務，即當li+4=lj，且lj+4=ll，先安排岸橋執行lj貝位上的 j任務。目的是方便后來的任務i和任務 j被不同的岸橋同時作業。

步驟3如果該船舶有重點路，則運用有重點路情況下的啟發式算法。具體步驟如下：

第3.1步：結合挖孔作業思想，安排作業速度最快的岸橋作重點路任務。

第3.2.1步：如果li和lj是重點路任務，li+4=lj，且lj+4=ll，那么安排作業速度最快的岸橋k作lj貝位上的 j任務。

第3.2.2步：如果li和lj是重點路任務，li+4=lj，且lj+4≠ll，ll+4≠li，那么可以安排作業速度最快的岸橋從重點路的任意一個貝位開始執行任務。

第3.3步：如果li+4=lj，且lj+4=ll，安排岸橋作lj貝位上的任務；再根據貝位上的優先任務順序執行。

第3.4步：岸橋的替接移動。當岸橋QC1完成li貝位上的任務，li+4=lj，且岸橋QC2在執行ll貝位上的任務，lj+4=ll；即當兩項任務的間隔距離dij≥8時，當其中一臺岸橋有空閑時，可以發生一次替接移動。兩臺岸橋同時向有未完成任務的方向移動，形成兩臺岸橋平行作業。

第3.5步：岸橋在完成一項任務時，去執行距離它最近的任務。岸橋任務依次循環，直至所有任務都被執行結束。

步驟4如果沒有重點路，則用沒有重點路情況下的啟發式算法。具體步驟如下：

第4.1步：將總的裝載箱量除以作業路數，得到平均每路作業的箱量。

第4.2步：按前后順序將任務分配給各作業路。

第4.3步：對分配給各路的作業，結合挖孔思想，先安排各岸橋執行柱形圖中的高柱貝位任務。

第4.4步：岸橋的替接移動。當岸橋QC1完成li貝位上的任務，li+4=lj，且岸橋QC2在執行ll貝位上的任務，lj+4=ll，即當兩個任務的間隔距離dij≥8時，當其中一臺岸橋有空閑時，可以發生一次替接移動。兩臺岸橋同時向有未完成任務的方向移動，形成兩臺岸橋平行作業。

第4.5步：岸橋在完成一項任務時，根據各作業路任務群去執行距離它最近的任務。岸橋任務依次循環，直至所有任務都被執行結束。

4.2.2 啟發式算法階段2

階段2在初始值基礎上，進行局部調整，尋求最優解。

根據岸橋作業的均衡化原則，及各岸橋的相應任務的同步性原則，在初始值的基礎上進行局部調整，得到新解。如果求得的新解優于當前解，則更新當前解；否則，繼續迭代，直到得到滿意解。

5 算例

5.1 算例數據

計算數據為寧波某集裝箱港口數據。具體數據見表1～表4。表4為兩兩任務距離表。另外岸橋的單位貝位移動時間t為0.003 h，岸橋間的最小距離為8個貝位距離。

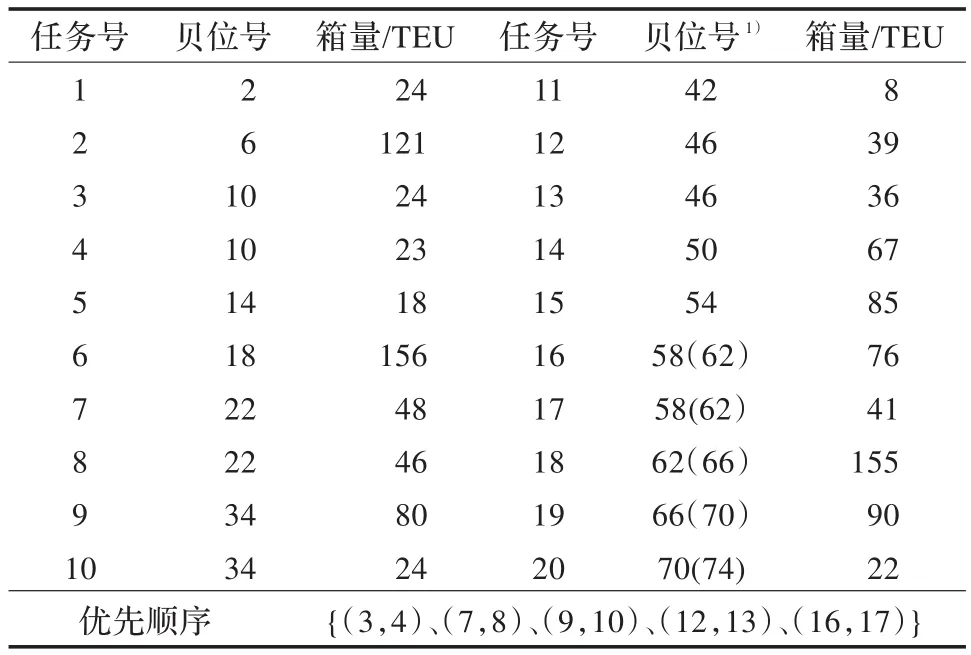
表1 船舶裝卸任務數據表

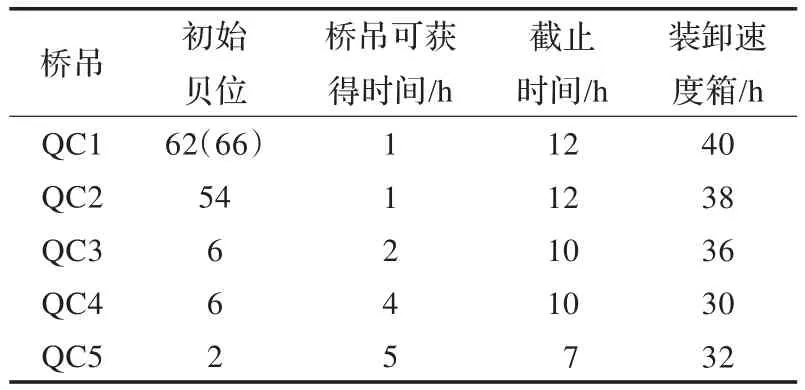
表2 岸橋數據表

5.2 模型P2解算

采用上述數據，運用LINGO9.0軟件對P2模型進行求解。在惠普6515bADM Athlon64 X2雙核處理器、內存為1 GB和硬盤為160 GB的個人計算機上，運行了24.5 h，得到了全局最優解，最短完成時間9.971111 h，它為模型P1的下限邊界值。詳細求解結果如表5，每臺岸橋的工作任務、完成時間和左右最小移動時間。

表3 岸橋首個任務距離表

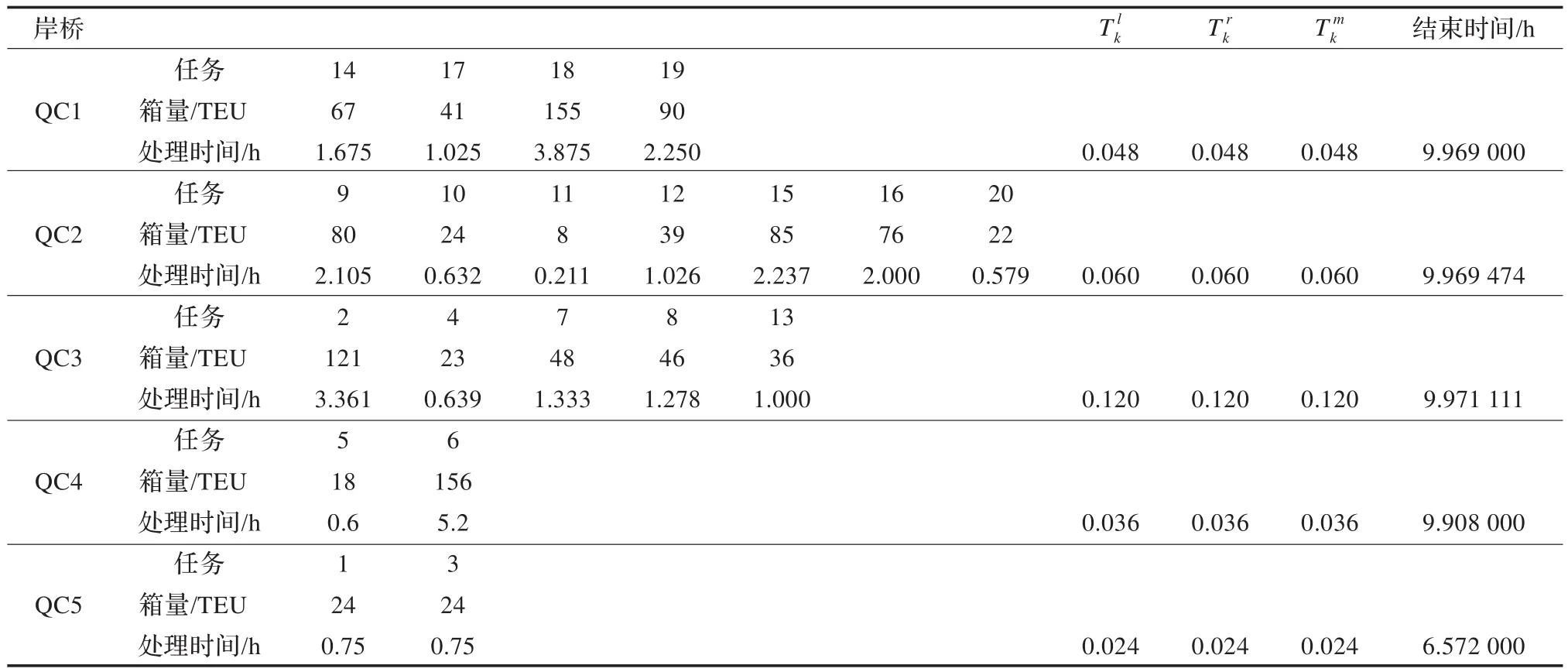
表5 簡單模型P2求解結果

5.3 基于規則的啟發式算法解算P1

同樣采用上述數據，根據3.2節所述基于規則的啟發式算法對模型P1進行求解，得到船舶的岸橋調度時序表如表6～表10。

5.4 數據分析

對模型P2和模型P1的求解結果（表11）進行比較，發現目標值從9.971111 h上升到10.427 h，增加了0.456 h。但是模型P2中有些岸橋的某些任務安排不符合港口實際，如岸橋在實際執行任務時不能相互跨越；模型P2中的岸橋1的任務14，岸橋2的任務20。

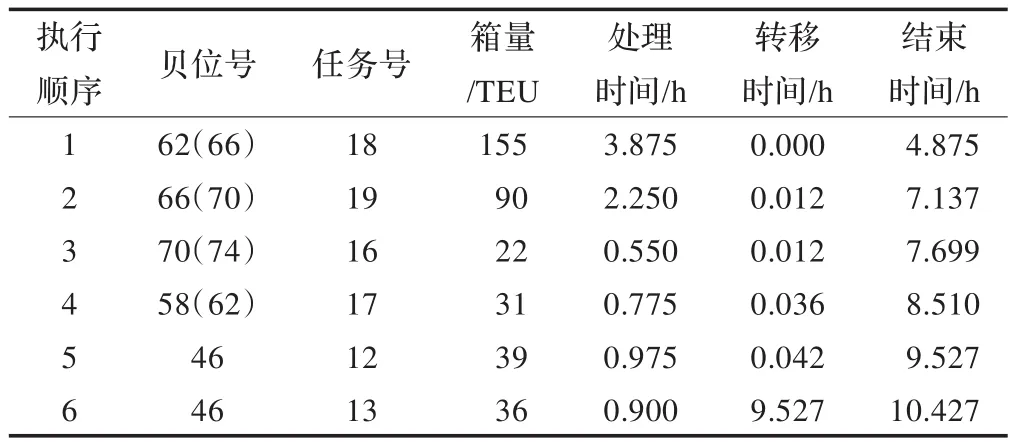
表6 QC1調度時序表1）

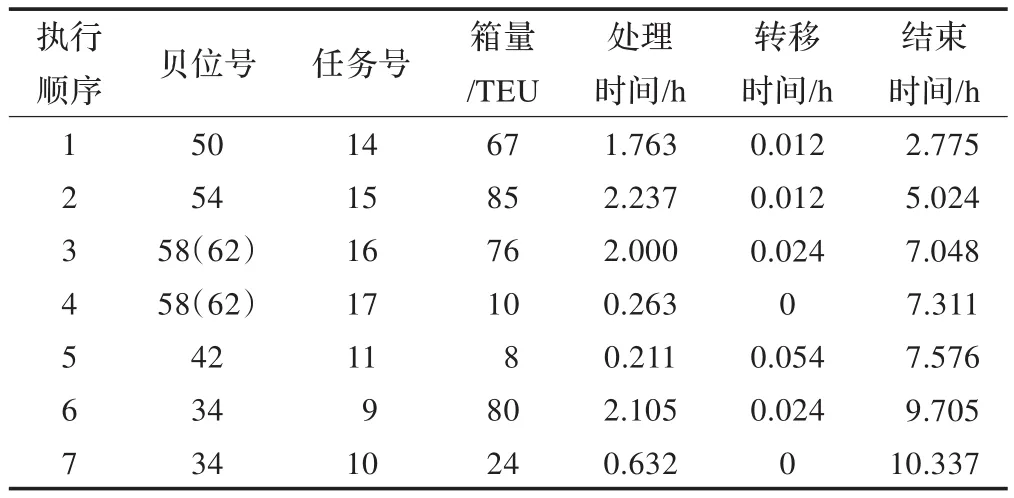
表7 QC2調度時序表1）

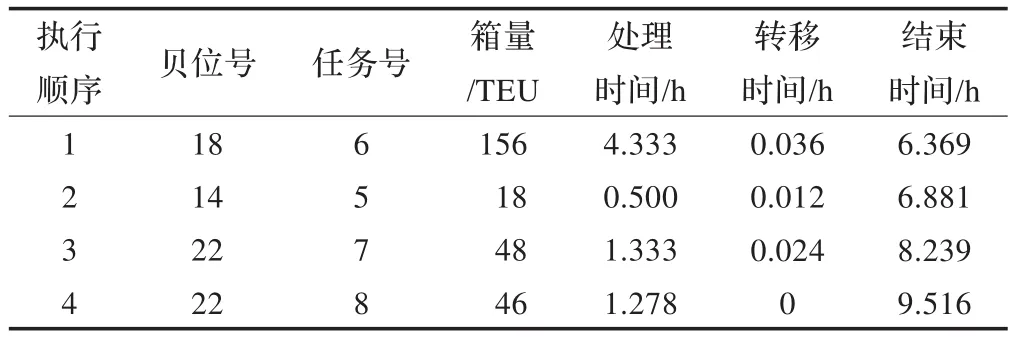
表8 QC3調度時序表1）

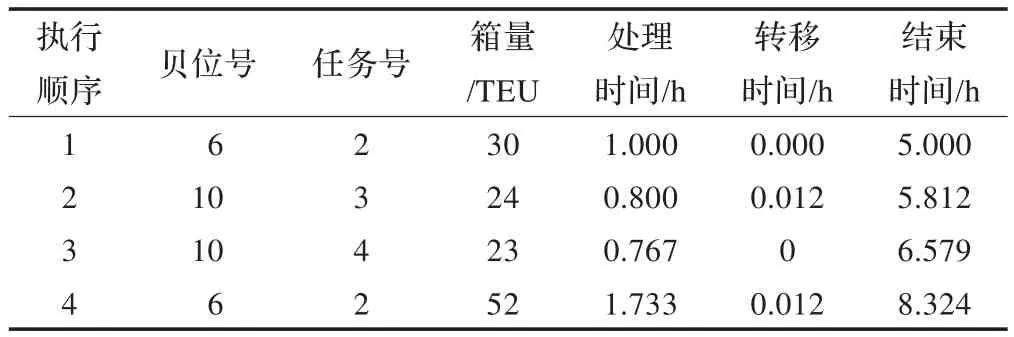
表9 QC4調度時序表1）

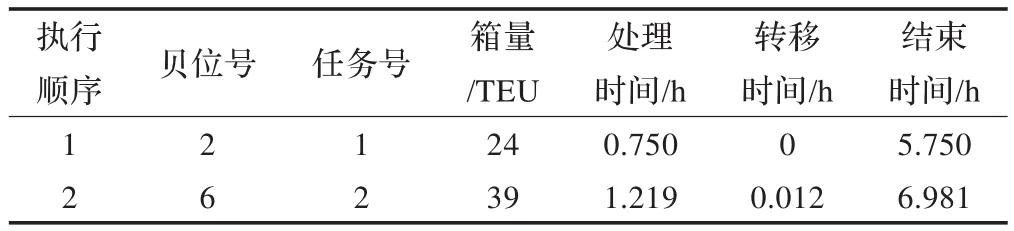
表10 QC5調度時序表1）

表11 兩種方法結果比較表

由模型1的岸橋調度時序表，可得到任務銜接圖（圖4）。由圖4可以直觀看出各岸橋的相應任務完成時間很接近，這與港口的實際操作相符；另外各岸橋均在時間窗內作業。由此可見：該艘船舶的岸橋調度時序表和目標值10.427 h是符合實際的較好的滿意解。

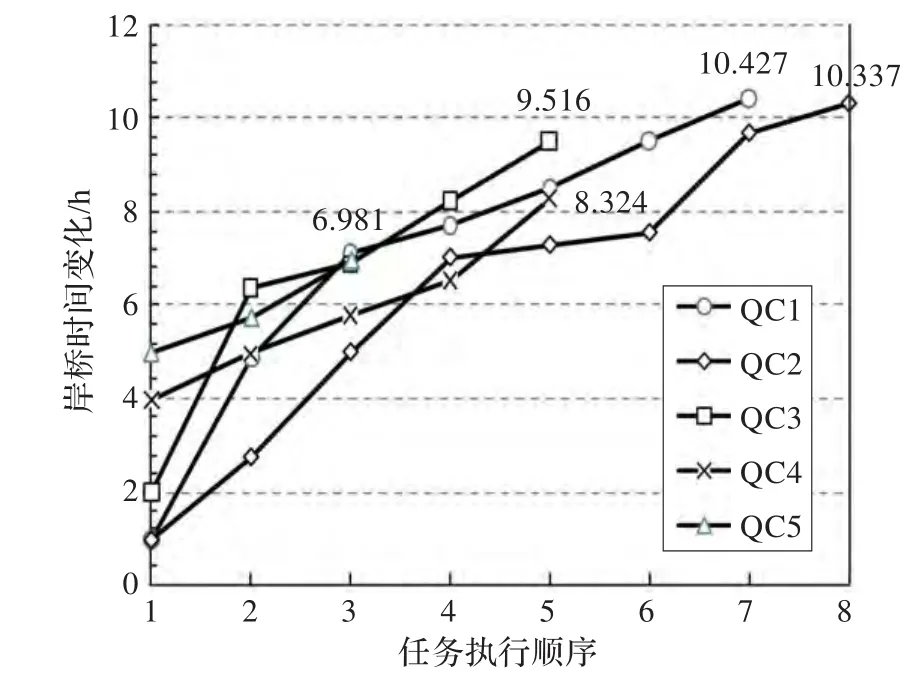
圖4 單艘船舶岸橋任務時間分布圖

6 結語

岸橋調度研究有利于縮短船舶在港作業時間，提高港口生產率。本文的主要創新點是在注重理論研究的基礎上，更加關注實際應用，表現在：一是考慮了岸橋屬性中岸橋的時間窗、裝卸速度等實際因素。二是根據港口中控人員的實際操作，抽象出岸橋的工作原則，提出了基于規則的啟發式算法，將其求解結果與下限值進行比較分析，發現該解屬于較好的滿意解。

本文的不足之處是沒有考慮其他設備（集卡、龍門吊）對岸橋調度問題的影響，也沒有考慮實際港口作業中的隨機因素影響，如岸橋故障、天氣的影響。因此，隨機因素可作為進一步研究的方向。

[1]Steenken D，Winter T，Zimmermann U T.Stowage and transport optimization in ship planning[M]//Grotschel M，Krumke S，Rambau J.Online Optimization of Large Scale Systems.Berlin：Springer，2001：731-745.

[2]Kim K H，Park Y M.A crane scheduling method for port containerterminals[J].European JournalofOperational Research，2004，156：752-768.

[3]Moccia L，Cordeau J F，Gaudioso M，et al.A branch-andcut algorithm for the quay crane scheduling problem in a container terminal[C]//AIRO Annual Conference，Cameerino，Italy，2005.

[4]Da Hunjung，Park Y M，Lee B K，et al.A quay crane scheduling method considering interference of yard cranes in container terminals[C]//LNAI 4293：Proceedings of the Fifth Mexican International Conference on Artificial Intelligence（MICAI2006）.Berlin Heidelberg：Springer-Verlag，2006：461-471.

[5]Sammarra M，Cordeau J F，Laporte G，et al.A tabu search heuristic for the quay crane scheduling problem[J].Journal of Scheduling，2007，10：327-336.

[6]Lee Der-Horng，Wang Huiqiu，Miao Lixin.Quay crane scheduling with non-interference constraints in port container terminals[J].Transportation Research Part E，2008，44：124-135.

[7]Tavakkoli-Moghaddam R，Makui A，Salahi S，et al.An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports[J].Computers&Industrial Engineering，2009，56：241-248.

[8]Bierwirth C，Meisel F.A fast heuristic for quay crane scheduling with interference constraints[J].Journal of Scheduling，2009，12：345-360.

[9]Zhang Haipeng，Kim K H.Maximizing the number of dualcycle operations of quay cranes in container terminals[J].Computers&Industrial Engineering，2009，56：979-992.

[10]Cao Jinxin，Shi Qixin，Lee Der-Horng.Integrated quay crane and yard truck schedule problem in container terminals[J].Tsinghua Science and Technology，2010，15：467-474.

[11]Meisel F.The quay crane scheduling problem with time windows[J].Naval Research Logistics，2011，58（7）：619-636.

[12]Legato P，Trunfio R，Meisel F.Modeling and solving rich quay crane scheduling problems[J].Computers&Operations Research，2012，39：2063-2078.

[13]Meisel F，Bierwirth C.A survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research，2010，202：615-627.