基于組合模型的原子鐘時差數據修正算法

翟靜董蓮 陸福敏張樹生

Zhai Jing1,2 Dong Lian2 Lu Fumin2 Zhang Shusheng1

1.中國計量學院 機電工程學院，浙江 杭州 310018

2.上海市計量測試技術研究院，上海 201203

1. College of Electrical and Mechanical Engineering China Jiliang University Hangzhou 310018;

2. Shanghai Institute of Measurement and Test Technology, Shanghai 201203

1 引言

原子鐘廣泛應用于守時系統或衛星導航系統中，基于完好性，這些系統均需要對原子鐘進行檢測，然而在原子鐘運行過程中，任何測量比對系統可能會由于外界因素造成測量數據的突變，如外電系統突然斷電、鐘失鎖或比對系統故障等，導致系統采集的數據不完全反映原子鐘的性能。因此，在利用比對數據進行時間尺度的計算前必須對其進行分析，檢測并修正錯誤或丟失的數據。目前。常用的修正方法就是考慮原子鐘過去數據的變化趨勢，利用二次多項式模型進行修正[1]，盡管能夠預報丟失的數據，但隨著丟失數據點的增多，預報誤差逐漸增大，預報精度降低。

本文利用灰色模型對原子鐘丟失數據進行預報并修正，盡管預報的時差數據精度較二次多項式模型有所提高，但仍不理想。通過對二次多項式模型和灰色模型的預報殘差分析，建立了兩種組合模型來對原子鐘丟失的時差數據進行修正。

2 數學模型

理想情況下,原子鐘的時差模型主要由初始相位偏差、初始頻率偏差和線性漂移三部分組成.在實際應用中,時間偏差 x(t)的數學模型用下式表示[2]:

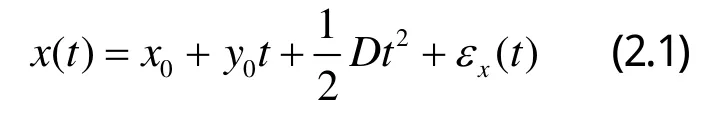
其中 x0為原子鐘的初始相位偏差, y0為原子鐘的初始頻率偏差,D為原子鐘的線性漂移,為原子鐘隨機噪聲所引起的變化量。

2.1 二次多項式模型

由式2.1知，原子鐘讀數T和系統時間t之間的關系可以用一個二次多項式表示[2]：

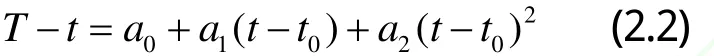
其中a0、a1和a2分別是t0時刻原子鐘相對于系統時間t的鐘差、鐘速(頻差)和半加速度(頻率漂移的一半)。

設相對于時間 t1，t2,…,tn，觀測誤差為 e，根據式2.2可建立誤差方程

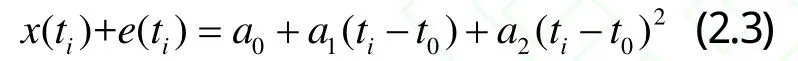
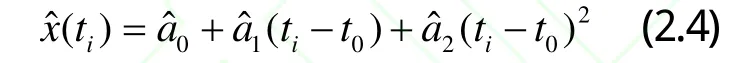
根據最小二乘估計原則，記

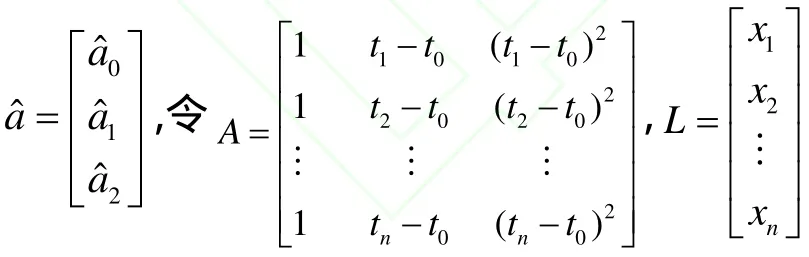
由最小二乘原理得估計值

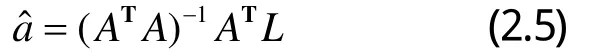
采用二次多項式模型進行丟失數據修正，其實質是利用過去數據，通過最小二乘法擬合后的曲線預測缺失點數值，但由于僅依賴過去數據變化的特點，未考慮公式 2.1中隨機誤差項會造成丟失點數據的實際應測值逐漸偏離擬合曲線，使得隨著丟失數據個數的增加，預測誤差逐漸積累，修正精度越來越差。

2.2 GM(1,1) 灰色模型

GM(1,1)灰色模型是將原子鐘時差的變化過程看做一個隨時間變化的灰色過程[3][4]，它由只包含單變量的一階微分方程構成，適用于對本身數據的預測[5]。

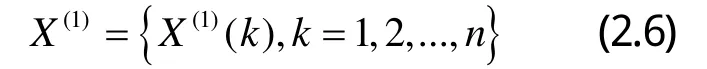
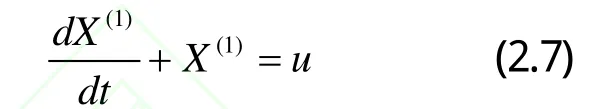
即GM(1,1)模型，其解為：

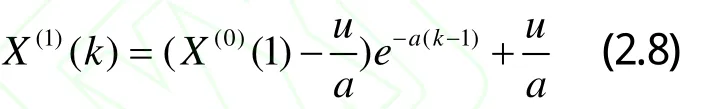
式中：k為時間序列，a為發展灰度，u為內生控制灰度。

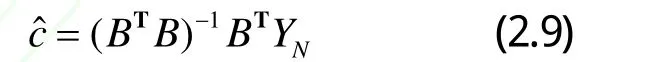
式中：B為數據陣；YN為數據列,B和YN的表示如下：

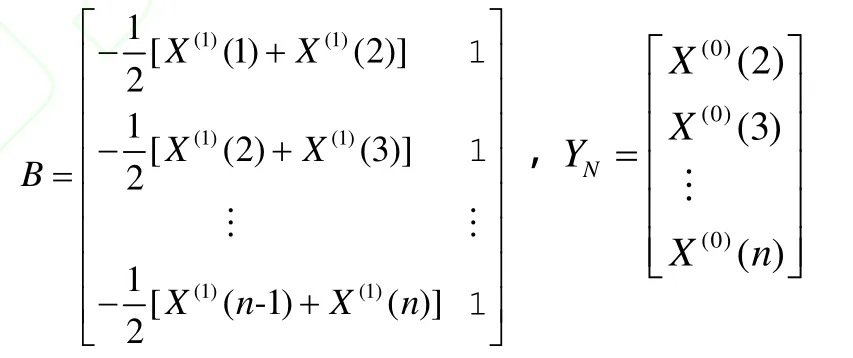
則最終預測值如下所示

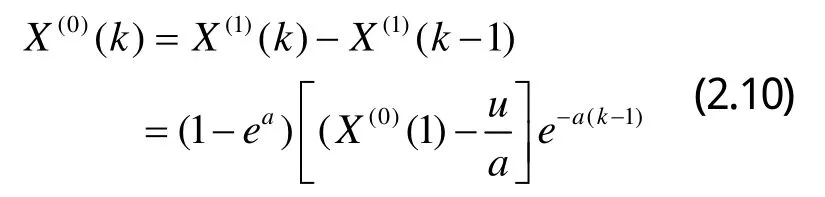
2.3 組合模型

針對二次多項式模型的缺陷，筆者提出了兩種組合模型來進行時差的預報和修正，兼顧考慮了丟失點前后數據列的變化特點，減小隨機誤差項對丟失點數據預測的影響。

設m為丟失數據點數，2n為參與修正的實際觀測數據的個數，算法流程如圖1所示。設Δt?為丟失數據初次建模后估值，為其二次建模后預估值，為最終預報值。

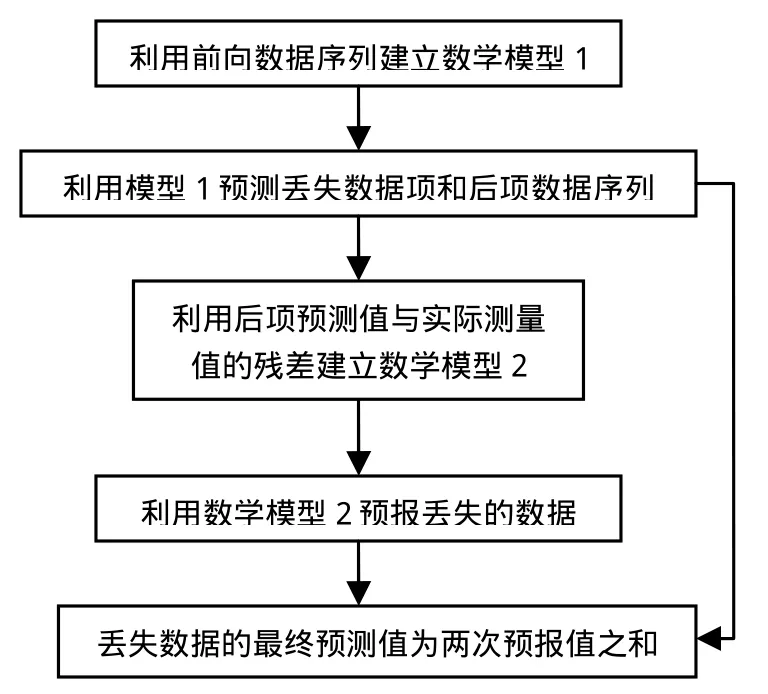
圖1 組合模型算法流程

2.3.1 組合模型1

對于組合模型1，前向數據采用二次多項式模型建模，并對丟失點數據和后項數據進行預測，其中丟失點的預測值滿足如下公式：

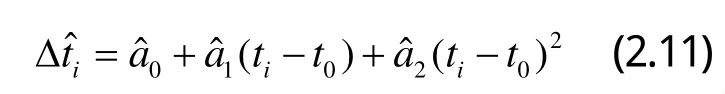
利用后項數據的預報值與其實際觀測值的殘差建立二次多項式模型，對丟失點數據進行預測，其預測值滿足如下公式：

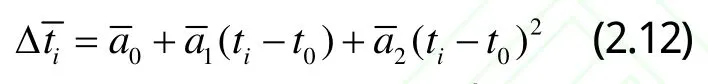
因此丟失點最終預測值itδ為：

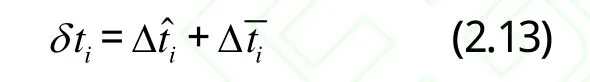
式中i=n+1,n+2,…,n+m。

2.3.2 組合模型2

對于組合模型2，前向數據采用灰色模型建模，對丟失點數據和后項數據進行預測，其中丟失點的預測值滿足如下公式：

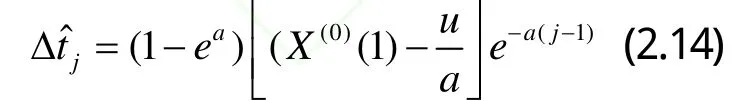
利用后項數據的預報值與其實際觀測值的殘差建立二次多項式模型，對丟失點數據進行預測，其預測值滿足如下公式：

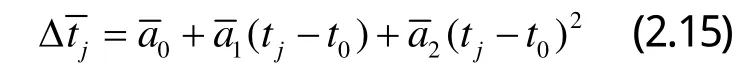
因此丟失點最終預測值jtδ為：

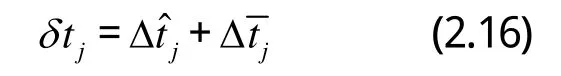
式中j=n+1,n+2,…,n+m。

3 算例分析

本文采用兩臺銫原子鐘與主鐘的小時差比對數據進行分析。丟失點的前向數據和后項數據長度可根據條件設定，當數據個數較少時，進行建模的信息點較少，預測精度較差，當數據個數較多時，預測精度高，但要求對系統進行長時間的觀測。為驗證四種模型的優劣，前向數據和后項數據分別采用48小時的時差數據。由于在守時系統中，丟失點數據個數超過10個時(即10小時數據)，此鐘將不再參與地方原子時的計算[7]，因此假設丟失8小時數據。

測試方案：方案1：用二次多項式模型對丟失點預測；方案2：利用灰色模型對丟失點預測；方案三：利用組合模型1對丟失點預測；方案四：利用組合模型2對丟失點預測。比較結果如表1和圖2、圖3所示。

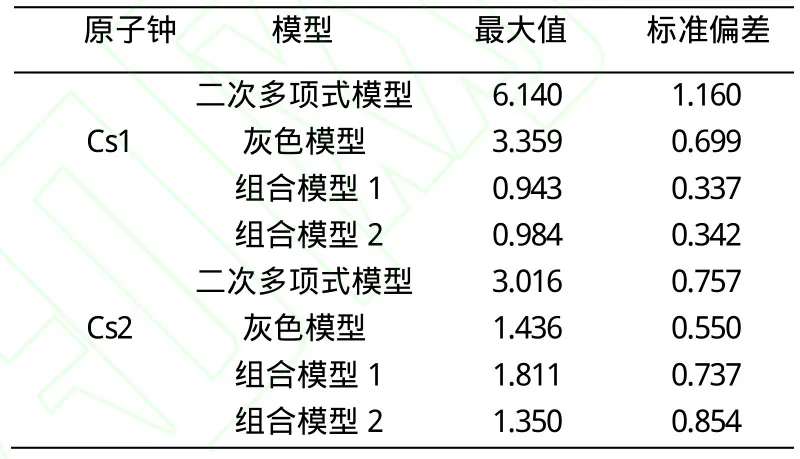
表1 四種模型對丟失點預報殘差的比較(單位：ns)

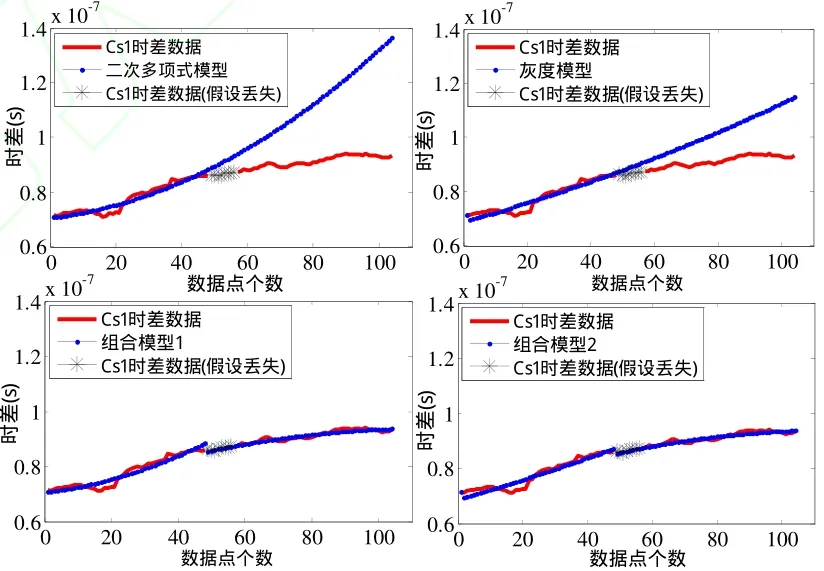
圖2 利用四種模型預測原子鐘Cs1丟失數據點

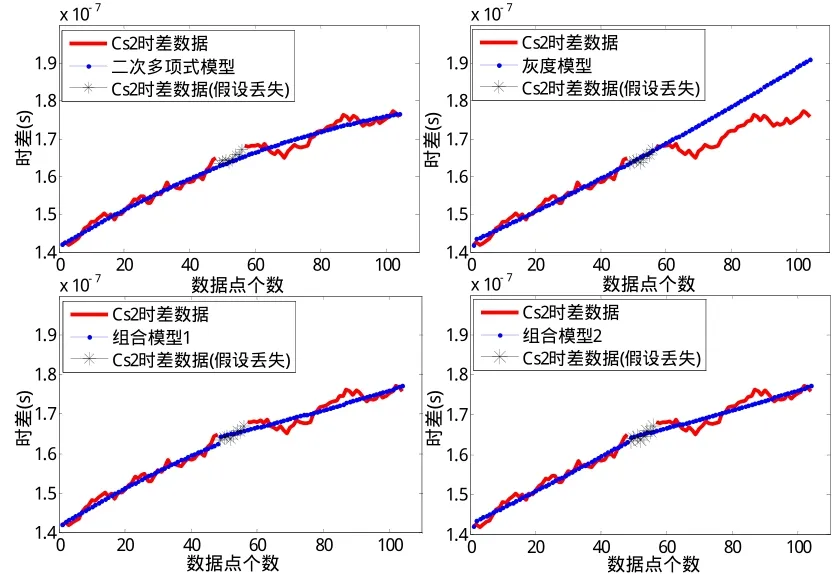
圖3 利用四種模型預測原子鐘Cs2丟失數據點

通過以上算例可以分析出：

(1) 如圖2所示，當原子鐘丟失點的前向數據上下波動性較強時，所建模型受局部波動影響較大，因此原子鐘Cs1采用二次多項式模型和灰色模型都無法精準的預測丟失數據，誤差較大。如圖3所示，當前向數據規律性較強、波動不大時，原子鐘Cs2采用二次多項式模型和灰色模型能夠較好的預報丟失數據，其中灰色模型的預測精度高于二次多項式，這表明灰色模型更適合于對上下波動不大的數據建模；

(2)采用兩種組合模型進行預報時，能取得較高的預報精度，優于二次多項式模型：對于Cs1而言，采用兩種組合模型，其預測精度較二次多項式模型和灰度模型均提高了一個數量級，對于Cs2而言，兩種組合模型的預測精度較二次多項式模型有所提高；

(3)對于兩種組合模型而言，對前項數據選擇何種模型需要考慮數據本身的變化特性，對變化平穩、規律性較強的數據建模時，應選擇組合模型2，而當前向數據上下波動性較強時，應選擇組合模型1進行丟失數據預測并修正。

4 結束語

二次多項式模型預報丟失數據具有很大的弊端，而采用灰色模型進行預報并修正時，盡管精度有一定程度的提高，但仍不理想，這主要是沒能充分利用系統信息，忽視了丟失點后項時差序列的變化趨勢和原子鐘隨機誤差影響導致，而采用兩種組合模型預測，兼顧考慮了丟失數據前后的時差序列變化趨勢，能夠取得較高的精度，因此，在原子鐘數據分析中具有一定的實用性。

[1]朱亞敏.守時系統用戶信號監測方法研究與軟件設計[D].西安: 中國科學院國家授時中心,2010:30-36.

[2]郭海榮.導航衛星原子鐘時頻特性分析理論與方法研究[D].鄭州:信息工程大學測繪學院，2006:92-94.

[3]路曉峰,賈小林,崔先強.灰色系統理論的優化方法及其在衛星鐘差短期預報中的應用[J].測繪工程,2006,15(6):12-15.

[4]朱凌鳳,唐波,李超.兩種模型用于衛星鐘差預報的性能分析[J].飛行器測控學報, 2007,26(3):39-43.

[5]朱凌風,吳曉平,李超,等.灰色模型在衛星鐘差預報中的缺陷分析[J].宇航計測技術,2007,27(4):42-44.

[6]劉永義,黨亞民,張承飛.一種組合模型在衛星鐘差長期預報中的應用研究[J].測繪科學，2012,37(2):17-19.

[7]何大林.守時數據處理及其可視化實現[D]. 西安: 中國科學院國家授時中心,2010:28-31.

[8]陳正生,呂志平,張華清,等.基于時間序列分解的 GPS衛星鐘差預報[J]. 測繪科學，2011,36(3):116-118.