細長三角翼滾轉/側滑耦合運動效應分析

楊小亮，劉偉，吳天佐，劉緒

(國防科學技術大學航天科學與工程學院宇航科學與工程系，湖南 長沙 410073)

0 引言

滾轉/側滑雙自由度耦合運動如圖1所示，戰斗機在繞體軸發生搖滾的同時，質心左右移動。這種耦合運動形式與荷蘭滾(Dutch Roll)現象有一定的相似之處:從后面看戰斗機就像鐘擺左右擺動，從上面看戰斗機沿蛇行路線前進，但滾轉/側滑雙自由度耦合的搖滾運動比荷蘭滾更為復雜。荷蘭滾是橫側小擾動模態［1］，可采用線性氣動模型描述，而搖滾是大迎角下的非線性氣動現象，必須采用非線性的氣動模型進行研究。

研究多自由度耦合的運動特性具有實際意義，賈區耀［2-3］在對飛行器大氣自由飛的結果和風洞實驗數據進行對比分析時就發現，風洞實驗或數值計算表明是穩定的某些飛行器，自由飛的結果卻是不穩定的，分析認為自由度不相似可能是導致這些差異的重要原因之一。事實上，真實飛行條件下，搖滾現象通常是多自由度耦合的運動，因此，根據飛行器運動的特點，分析并滿足主要的自由度相似，研究多自由度耦合的翼搖滾特性是非常必要的。

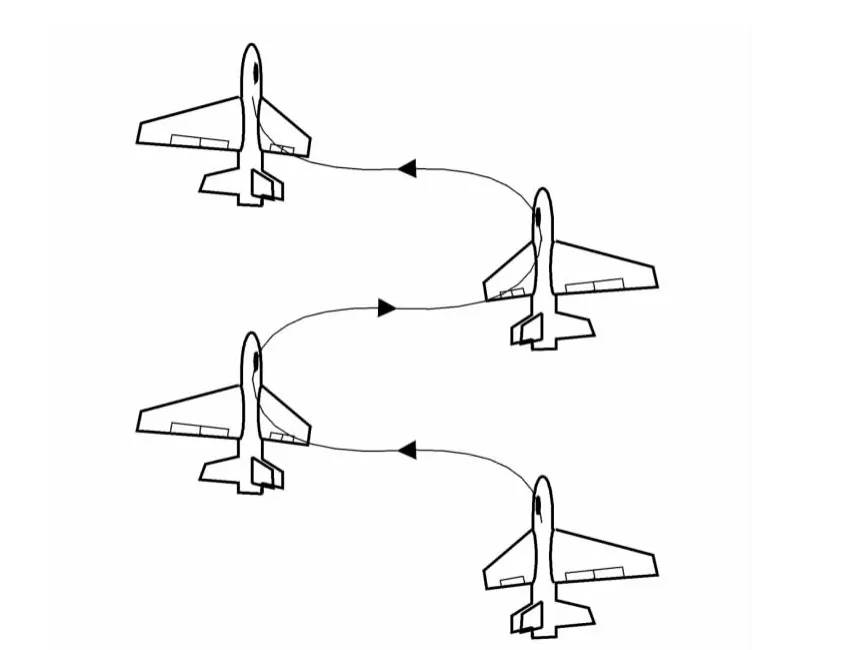
圖1 飛行器滾轉/側滑耦合運動示意圖Fig.1 Schematic of aerocraft in combined free roll and free sideslip motion

三角翼結構簡單、流場中有豐富的渦結構，被認為是動態特性研究最理想的對象之一，國內外涌現了大量針對三角翼開展的動態實驗和數值模擬研究，也取得了重要的進展。通過分析發現，這些研究主要針對三角翼單自由度俯仰或滾轉的運動特性，僅有少量文獻涉及了多自由度耦合運動，文獻［4-5］研究三角翼俯仰/滾轉耦合運動特性，文獻［6］則對三角翼滾轉/側滑耦合運動進行探索，可見對多自由度耦合運動特性的研究還很不充分。另外，文獻［7-8］采用純強迫運動研究三角翼的耦合運動，雖然能夠從一定程度反映三角翼氣動力/力矩的遲滯特性，但對縱橫向運動交感耦合特性的模擬有其無法回避的局限性。

除滾轉自由度外，搖滾過程中的側力，可導致戰斗機在搖滾同時發生側滑運動，因此，側滑也是主要自由度之一。本文數值模擬尖銳前緣的80°后掠平板三角翼自由滾轉、自由側滑雙自由度耦合的運動特性，并與單自由度翼搖滾比較，分析三角翼滾轉/側滑耦合的運動機制，研究耦合運動過程中的耦合效應及其流場特性。

1 研究方法

數值模擬研究細長三角翼自由滾轉、自由側滑的耦合運動，需要建立滾轉/側滑雙自由度耦合運動的模型，采用合理的數值方法離散控制方程組，然后生成計算網格數值模擬三角翼非定常的動態運動過程。

1.1 滾轉/側滑雙自由度耦合運動模型

本文研究的雙自由度運動涉及自由滾轉和自由側滑，將轉動運動方程建立在體坐標系下可以保持三角翼轉動慣量為常量，將質心運動方程建立在慣性坐標系中便于描述三角翼質心的運動。三角翼耦合運動的無量綱控制方程組可寫為:

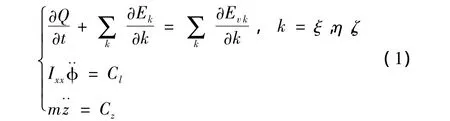
式中Ek和Evk分別為對流通量和粘性通量，φ和z分別為滾轉角和慣性系下質心Z坐標，Cl和Cz分別為滾轉力矩系數和側向力系數，無量綱轉動慣量Ixx和無量綱質量m分別為:

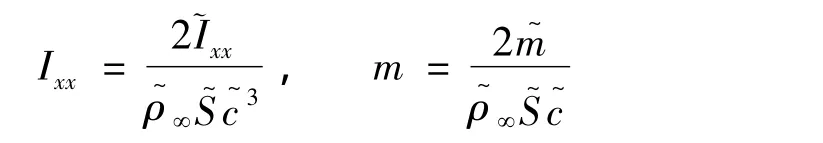
帶上標“～”表示有量綱量，式中S～和 c～分別表示參考面積和參考長度。由此建立了三角翼自由滾轉、自由側滑雙自由度耦合的動力學方程組，采用無量綱化的NS方程組作為流動控制方程組，則構成對三角翼滾轉/側滑雙自由度運動的完整描述，可應用適當的數值方法進行離散求解。

1.2 數值方法

采用二階迎風型NND格式［6］有限體積離散流動控制方程組的空間導數項，采用含雙時間步的LUSGS方法［7］來提高時間求解的效率和精度。三角翼背風面的流動具有典型的湍流特征，引入基于工程經驗和量綱分析的SA模型［8］模擬三角翼上多渦流結構的湍流效應。

剛體動力學方程組采用二階精度的單邊差分離散求解，流動控制方程組和剛體動力學方程組采用松耦合算法求解。

計算時，遠場邊界的處理采用基于Riemann不變量、適用于動態運動的無反射邊界條件［9］。壁面邊界，速度采用無滑移條件，溫度采用絕熱壁條件，壓力條件計入離心力的影響。

1.3 三角翼模型及網格

計算采用80°后掠的三角翼模型，前緣及尾緣采用向下削尖處理。對于這類具有尖銳前緣的外形，生成OH型的計算網格能夠較好平衡模擬精度和網格規模［10］。本文采用的計算網格整體情況如圖2所示，網格大小為73×77×47，對應流向、周向和法向，網格上游邊界距離三角翼的頂點3倍根弦長度，周向邊界分別距離體軸3倍根弦長度，下游邊界距離三角翼的尾緣5倍根弦長度。截面網格采用O型拓撲結構，壁面第一層網格法向尺度控制為5×10-5倍根弦長度，利用Laplace方程作適當正交優化。

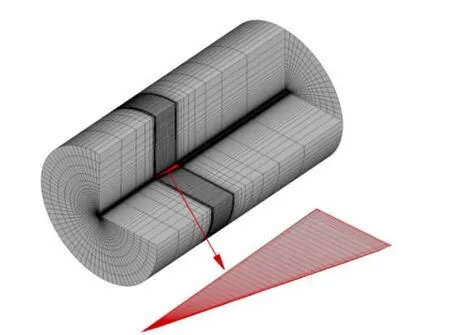
圖2 80°后掠三角翼模型及空間網格分布Fig.2 The 80°swept delta wing model and space computational grid distribution

2 結果及分析

2.1 三角翼滾轉/側滑耦合搖滾特性及與單自由度搖滾特性的比較

首先數值模擬三角翼的單自由度自激搖滾特性，作為對程序的考核，并用于與三角翼雙自由度耦合搖滾運動特性的比較，研究側滑自由度對搖滾特性的影響。采用來流馬赫數Ma=0.35，基于根弦長度的雷諾數Re=2.5×106，三角翼繞體軸的無量綱轉動慣量Ixx=0.0622，給定30°名義迎角和0°初始滾轉角，三角翼單自由度搖滾特性如圖3所示。三角翼搖滾振幅逐漸增大，經過10個周期的發展，形成頻率穩定的、極限環形式的、振幅約為37.7°的自維持等幅振蕩。圖3(b)所示的搖滾相曲線顯示三角翼的搖滾逐漸收斂到極限環形式的周期吸引子形態。國內外實驗和數值模擬研究表明，細長三角翼單自由度搖滾表現為極限環形式的周期性等幅振蕩，由于模型加工、支架安裝以及軸承摩擦等因素的影響，這些結果之間存在著一定的差異。本文模擬得到三角翼單自由度自激滾轉的振幅約 37.7°，與實驗［11］和數值模擬［9］結果(振幅在30°～40°)能夠較好的吻合。

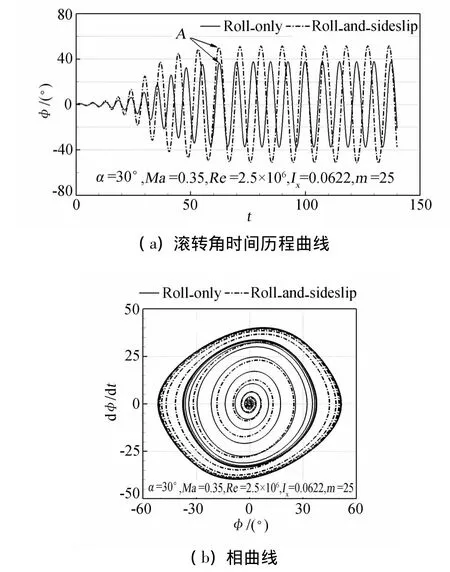
圖3 滾轉/側滑耦合運動與單自由度自激搖滾運動特性的比較Fig.3 The comparison of characteristics between combined roll and sideslip motion and wing rock

研究滾轉/側滑耦合的雙自由度運動涉及三角翼的轉動和平動，除轉動慣量外，還應指定三角翼的質量。采用與單自由度相同的計算條件，并指定三角翼的無量綱質量m=25.0，模擬80°后掠三角翼滾轉/側滑的雙自由度耦合運動，結果如圖3所示。同時允許自由滾轉、自由側滑條件下，三角翼從0°滾轉角位置開始，滾轉振幅逐漸增大，經過約9個周期的發展，形成振幅和頻率穩定的周期性等幅搖滾振蕩。在本文條件下，三角翼滾轉/側滑耦合運動的搖滾振幅約為51.5°，如圖3(a)所示，顯著大于單自由度自激搖滾時37.7°的振幅，雙自由度條件下滾轉運動的頻率較低、周期較長，雖然二者達到極限環形式的周期性振蕩所經歷的周期數不同，但所歷經的時間大致相同，圖中位置A所示。圖3(b)所示的相曲線上可以看到，在側滑自由度的影響下，三角翼滾轉運動的相曲線仍收斂到極限環形式的周期吸引子形態，在本文的質量和轉動慣量條件下，雙自由度耦合運動的極限環顯著大于單自由度搖滾的極限環，也就是說:在相同的滾轉角下，雙自由度條件下的滾轉角速度更大;在達到相同的角速度時，雙自由度條件下的三角翼所達到的滾轉角更大。

隨著市場經濟體制的發展以及與之相匹配的法律法規的完善，現代社會為個體追求和實現自我利益提供了相對公平的場域。 任何個人、團體都可以作為市場主體參與市場競爭，并以此實現自身的合法利益。 “為我”的利益訴求日益為更多的個體所認可，利益主體迅速多元化，市場成為“各種利益主體不斷角逐的活動過程”[2]。 在這一過程中，個體與個體之間，個體與社會群體之間、群體與群體之間的利益矛盾此消彼長、盤根錯節。

滾轉/側滑耦合運動的搖滾振幅與質量有關，進一步的計算表明，隨著質量增大，滾轉/側滑耦合的搖滾振幅有所減小，但三角翼滾轉/側滑雙自由度耦合條件下的搖滾振幅均大于單自由度搖滾的振幅。當質量特別大時(比如m=1000.0)，滾轉/側滑耦合運動的搖滾特性和單自由度搖滾的特性接近。

2.2 滾轉/側滑耦合運動的流場特性

為研究三角翼滾轉/側滑耦合運動時的流動機理，選擇極限環振幅建立后的一個滾轉“正”行程(ωx＞0)繪制截面流場，分析三角翼背風面的非定常流動特性。圖4是滾轉“正”行程x/c=0.67截面流向渦量Ωx隨滾轉角的演化，顯示前緣集中渦在翼面上的非對稱發展過程。虛線表示流向渦量Ωx＜0，實線表示流向渦量Ωx＞0。按照滾轉角的變化，該過程大致分為三個階段:

第一階段，圖4(a～d)，三角翼具有負滾轉角，翼面右側前緣產生的集中渦占主導，形成正的滾轉力矩，使三角翼滾轉角速率增大。右側翼面上除了主翼渦外，還有結構清晰的二次分離結構。隨著三角翼的滾轉，兩側渦非對稱增長，左側渦迅速增強，右側渦緩慢增長，由非對稱造成的滾轉力矩逐漸減小，因此，雖然三角翼滾轉的角速率持續增大，但角加速率越來越小。

第二階段，圖4(e)，此時三角翼位于0°滾轉角附近，由于滾轉導致的遲滯效應，右側渦較為貼近翼面，結構較為緊湊，翼面兩側渦強度大致相當，使三角翼滾轉的力矩顯著減小，滾轉的角速率接近極值。此時，由于左側渦顯著增強，其正下方靠近前緣的位置開始形成二次渦。

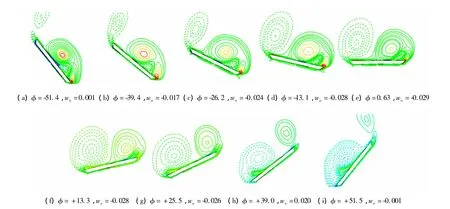
圖4 滾轉正行程(ωx＞0)截面(x/c=0.67)流向渦量Ωx的演化Fig.4 The evolution of sectional(x/c=0.67)streamwise vorticity in positive rolling procession

第三階段，圖4(f～i)，這一階段三角翼具有顯著的正滾轉角，翼面左側前緣產生的集中渦占主導，形成負的滾轉力矩，使三角翼的滾轉減速。在0°滾轉角位置附近，圖4(e)，翼面兩側的主渦強度相當，隨著三角翼左滾，背風面左右兩側的主渦非對稱減弱，左側渦強度緩慢減弱但更加靠近翼面，右側渦強度迅速衰減且遠離翼面，翼面兩側渦結構非對稱逐漸加劇，形成負的滾轉力矩，使得三角翼滾轉速率減小。

在第三階段滾轉減速的過程中，二次渦的發展與第一階段滾轉加速的過程不同。由于渦結構隨滾轉運動的遲滯特性:抬起一側翼面上二次渦區域隨著滾轉減速逐漸縮小，直至25.5°滾轉角時，圖4(g)中右側仍有顯著的二次渦區域，而在滾轉加速時，圖4(c)中左側翼面上這一特征不明顯;下沉一側翼面上二次渦區域隨著滾轉減速逐漸擴大，至最大滾轉角51.5°時達到最大，圖4(i)中左側，而在滾轉加速的過程中，下沉一側二次渦區域的范圍變化較小，圖4(a～d)中右側。由此可見，滾轉動態遲滯特性使得渦結構在滾轉加速和減速過程中的發展具有不同的特征。

圖4顯示在最大滾轉角位置，滾轉角速度為零，側滑速度也趨于零。在負滾轉角時，圖4(a～d)，三角翼背風面的外法向偏向圖中右側，法向力是沿外法線方向的，因此法向力的側向分量也指向圖中右側，將使得三角翼向右的側滑加速;滾轉角回到0°滾轉角位置時，圖4(e)，集中渦產生的法向力指向翼面上方，側向作用面積較小，沒有顯著的側向分量，三角翼以較大的速度繼續向右側滑運動;在正的滾轉角時，圖4(f～i)，上翼面前緣集中渦轉到左側，前緣集中渦產生的吸力區將產生向左的側力，使得向右的側滑減速，當達到最大滾轉角時，圖4(i)，右側滑速度趨于零。三角翼的右側滑停止以后，集中渦引起向左的側力，使得三角翼開始左側滑的加速，進入側滑運動的“正”行程，如此往復形成三角翼的側滑振蕩。

2.3 滾轉/側滑雙自由度耦合運動機制分析

正如翼搖滾命名所指，滾轉是最主要的自由度。導致三角翼側滑運動的側力源于法向力在側向的分量，伴隨三角翼滾轉運動所產生，與滾轉角的方向密切相關，因此三角翼側滑運動的頻率特性主要與滾轉運動相似。圖5是滾轉/側滑雙自由度耦合運動時滾轉角速度和側滑速度隨時間變化的曲線，如圖所示，二者幾乎是同頻率、反相位的關系。

依據2.2節對三角翼上渦流演化特性的分析以及圖5所示的運動學關系，可分析三角翼的雙自由度耦合運動機制。圖6是三角翼滾轉/側滑耦合運動的示意圖，采用飛行視角繪制，即從三角翼尾緣向頂點方向觀察，圖中彎轉細實線箭頭表示滾轉方向，水平粗虛線箭頭表示側滑速度方向。

在滾轉運動的“正”行程(ωx＞0，即左滾:左側翼面下沉，右側翼面上升，圖中①～⑤號位置)，位置①三角翼具有最大的負滾轉角，滾轉角速度和側滑速度都接近零，三角翼左右兩側翼面上渦流結構的非對稱形成正的滾轉力矩，使得三角翼左滾加速，負的滾轉角導致法向力存在向右的分量，三角翼向右側滑并加速，運動到位置②，形成左滾右側滑的運動;正的滾轉力矩和法向力向右的分量使得三角翼的左滾和右側滑進一步加速，到達位置③，這時左滾角速度和右側滑速度都接近極值(由于遲滯特性，左滾可能還會繼續加速，不完全等于極值)，形成滾轉“正”行程中最顯著的左滾右側滑運動;位置④，由于翼面兩側渦流位置和強度的非對稱狀況發生改變，形成負滾轉力矩使三角翼左滾減速，此外正滾轉角引起法向力向左的分量，使三角翼右側滑運動也減速，但仍保持左滾右側滑的運動狀態;隨著左滾和右側滑運動的進一步減速，運動到達位置⑤，三角翼左滾角速度和右側滑速度減小到零，三角翼左滾右側滑的過程終止。

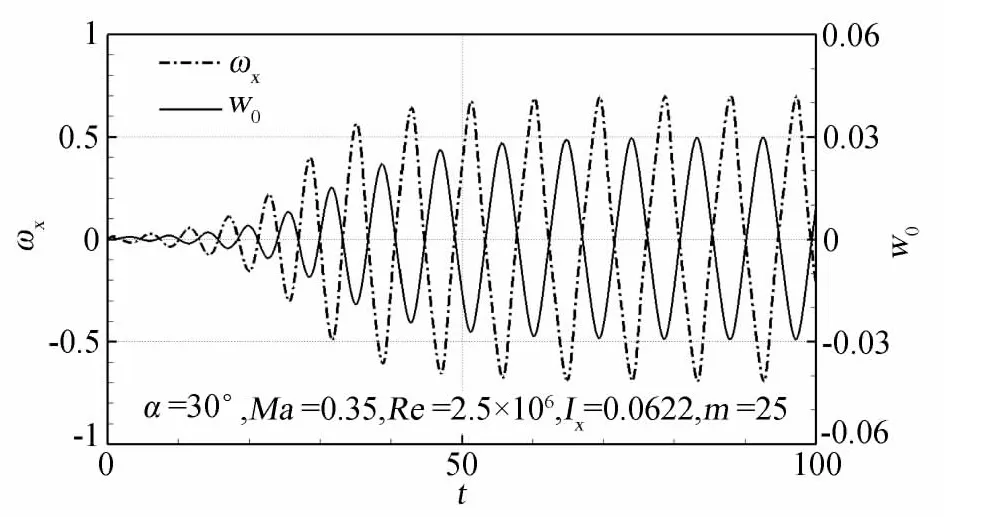
圖5 側滑速度和滾轉角速度時間歷程曲線Fig.5 The time history curves of sideslip velocity and roll angular velocity

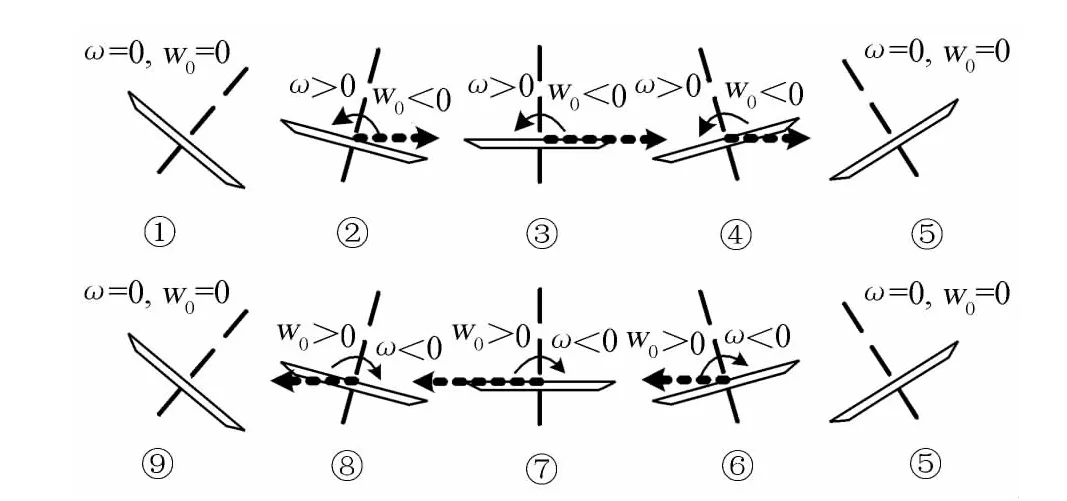
圖6 三角翼滾轉/側滑耦合運動機制示意圖Fig.6 Schematic of the kinematic coupling mechanism of combined free roll and free sideslip motion

滾轉運動的“負”行程(ωx＜0，右滾:右側翼面下沉，左側翼面上升，圖中⑤～⑨號位置)，與“正”行程的情況相反，以正行程終止的位置⑤為起始位置，該位置具有最大的正滾轉角，滾轉角速度和側滑速度都接近零，翼面上非對稱渦流結構產生負的滾轉力矩，使三角翼進入右滾，正滾轉角引起法向力向左的分量，三角翼開始左側滑加速，到達圖中位置⑥，形成右滾左側滑的運動;負的滾轉力矩和法向力向左的分量使得三角翼的右滾和左側滑進一步加速，到達位置⑦，此時左滾角速度和右側滑速度接近極值，形成“負”行程最顯著的右滾左側滑運動;到位置⑧，翼面兩側渦的位置和強度的非對稱狀況發生改變，正滾轉力矩使得三角翼右滾減速，正滾轉角引起向左的法向力分量，三角翼左側滑減速，但仍保持右滾左側滑的運動狀態;隨著右滾和左側滑運動進一步減速，運動到達位置⑨，三角翼右滾角速度和左側滑速度減小到零，三角翼右滾左側滑的過程終止。位置⑨和位置①的情況相同，三角翼又進入左滾右側滑，往復形成三角翼滾轉/側滑雙自由度耦合的運動。

綜上所述，三角翼滾轉/側滑雙自由度的耦合運動機制可以描述為:飛行視角下左滾右側滑，右滾左側滑的耦合運動。

2.4 滾轉/側滑運動的耦合效應分析

可以證明，三角翼單自由度搖滾的迎角和側滑角與滾轉角有如下關系:

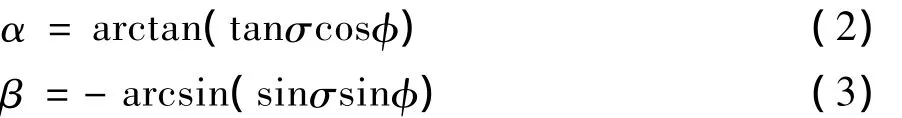
名義迎角σ為根弦與來流的夾角，等于初始時刻的迎角。由此可知單自由度條件下，σ不變時，迎角和側滑角與滾轉角一一對應。

然而滾轉/側滑耦合的運動，迎角和側滑角還受到無量綱側滑速度w0的影響，可以證明滾轉/側滑雙自由度耦合運動條件下，迎角和側滑角有如下表達式:

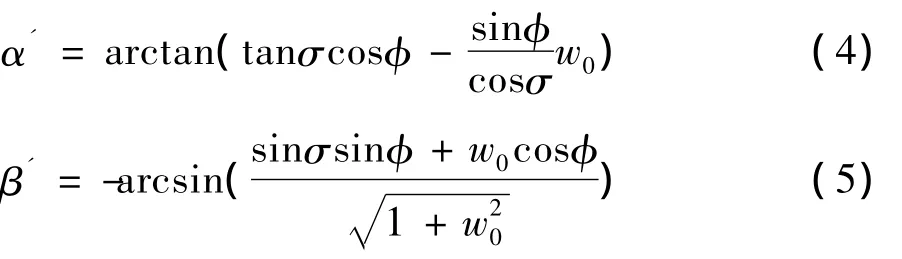
由圖5可知，滾轉/側滑耦合運動下，側滑運動并不劇烈，側滑速度比來流速度小兩個量級，可以作為小量處理，因此式可以簡化為:

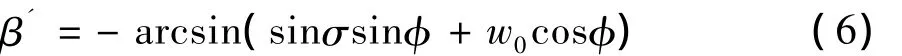
對比(6)式和(3)式，可求得側滑運動引起的側滑角增量dβ=β'－β表示為:

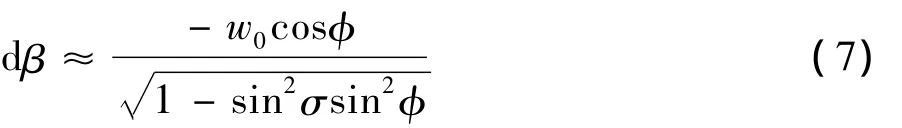
根據上式可知，側滑運動引起側滑角的增量與側滑速度符號相反，也就是說正的側滑速度引起側滑角減小，負的側滑速度引起側滑角增大。繪制側滑角隨滾轉角的變化，如圖7(a)所示，圖中實線為單自由度翼搖滾的側滑角，點劃線為滾轉/側滑耦合運動的側滑角。在滾轉運動的正行程，側滑運動導致三角翼的側滑角增大，在滾轉運動的負行程，側滑運動使得三角翼的側滑角減小，說明側滑運動導致了側滑角在搖滾過程中的遲滯效應，由2.2節的分析知，側滑速度與滾轉角速度反相，圖示的滯后效應與分析相符。圖7(b)是側滑運動引起的側滑角增量隨滾轉角的變化，曲線以順時針的螺旋線收斂到一個“菱形化的圓”，表明周期性的耦合搖滾形成以后，側滑運動將固定地在滾轉運動的正、負行程分別引起側滑角增大和減小。

同理可得，側滑運動引起迎角的增量為:

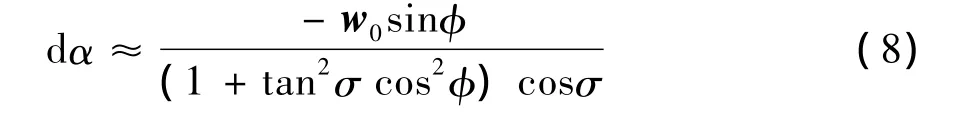
側滑速度與滾轉角速度反相，則三角翼在滾轉運動的正負行程經過同一滾轉角位置的側滑速度相反，由上式可知將引起符號相反的迎角增量，如圖8所示。可見，側滑運動的引入導致了迎角隨滾轉角的變化也產生了遲滯效應，加速滾轉的過程，側滑運動使得迎角減小，減速滾轉的過程，側滑運動使得迎角增大。

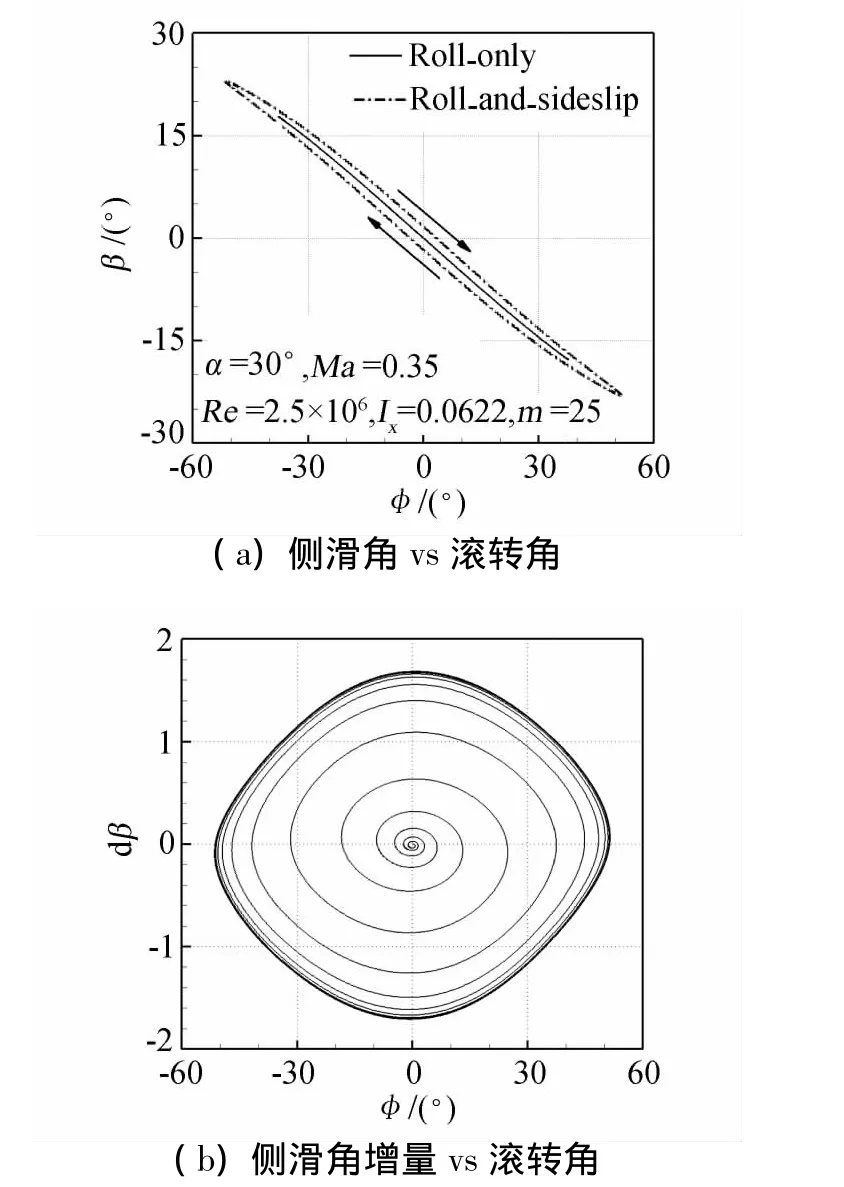
圖7 三角翼滾轉/側滑耦合運動對側滑角的影響Fig.7 Influence of the coupling effects in combined roll and sideslip motion on sideslip angle

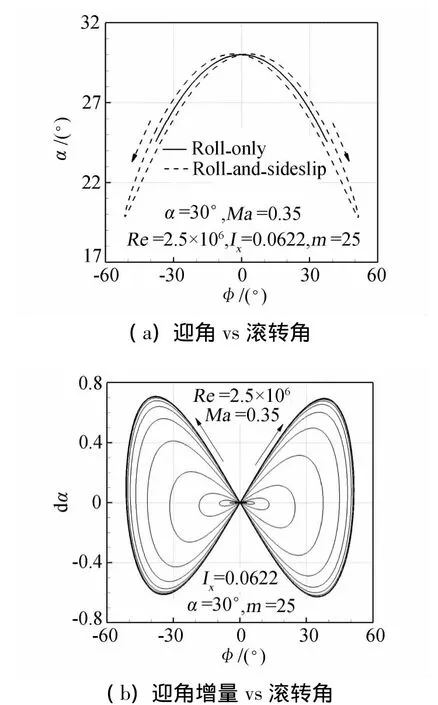
圖8 三角翼滾轉/側滑耦合運動對迎角的影響Fig.8 Influence of the coupling effects in combined roll and sideslip motion on attack angle

3 結論

(1)三角翼自由滾轉/自由側滑雙自由度耦合的搖滾運動比單自由度翼搖滾復雜，振蕩更劇烈:相同的滾轉角時，雙自由度耦合運動的滾轉角速度更大;在達到相同的角速度時，滾轉/側滑耦合條件下的三角翼所達到的滾轉角更大。

(2)滾轉/側滑雙自由度耦合運動條件下，渦流的非對稱遲滯特性仍是維持三角翼搖滾的流動機理;側滑運動強化了渦流的遲滯特性，引起迎角和側滑角隨滾轉角遲滯變化，從而加劇三角翼上渦流的非對稱變化，可能導致滾轉/側滑雙自由度耦合的搖滾更為劇烈。

(3)三角翼滾轉/側滑耦合的運動，滾轉是主要的自由度，側滑速度與滾轉角速度同頻率、反相位，左滾右側滑和右滾左側滑是三角翼滾轉/側滑雙自由度耦合運動的作動機制。

［1］胡兆豐，何植岱，高浩.飛行力學——飛機的穩定性和操縱性［M］.國防工業出版社，1985.

［2］賈區耀.天空飛行與地面風洞實驗動態氣動相關性研究［J］.實驗流體力學，2006，20(4):87-93.

［3］賈區耀，楊益農，陳農，天空飛行與地面風洞實驗動態氣動相關中的雷諾數影響［J］.實驗流體力學，2007，21(4):91-96.

［4］唐敏中，張偉，何宏麗.俯仰-滾擺耦合復雜流場試驗研究［J］.空氣動力學學報，2001，19(1):47-55.

［5］楊小亮，劉偉，趙云飛，劉君.80°后掠三角翼強迫俯仰、自由滾轉雙自由度耦合運動特性數值研究［J］.空氣動力學學報，2011，29(4):421-426.

［6］楊云軍，崔爾杰，周偉江.細長三角翼滾轉/側滑耦合運動的數值研究［J］.航空學報，2007，28(1):14-19.

［7］KANDIL O A，MENZIES M A.Coupled rolling and pitching oscillation effects on transonic shock-induced vortex-breakdown flow of a delta wing［R］.AIAA96-0828，1996.

［8］郭迪龍，楊國偉，康宏琳，王發民.三角翼受迫俯仰滾轉耦合運動的氣動特性研究［J］.空氣動力學學報，2007，25(1):65-69.

［9］SHEN Q，ZHANG H X.A new upwind NND scheme for Euler equations and Its application to the supersonic flow［A］.The Proceedings of ASIA Workshop on CFD［C］.Sichuan，China，1994.

［10］JAMESON A.Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings［R］.AIAA 91-1596，1991.

［11］SPALART P R，ALLMARAS S R.A one-equatlon turbulence model for aerodynamic flows［R］.AIAA 92-0439，1992.

［12］劉偉.細長機翼搖滾機理的非線性動力學分析及數值模擬方法研究［D］.［博士學位論文］.長沙:國防科學技術大學，2004.

［13］劉剛，周鑄，黃勇，等.三角翼大迎角繞流數值模擬中網格的影響研究［J］.空氣動力學學報，2004，22(4):481-485.

［14］NGUYEN L E，YIN L P，CHAMBERS J R.Self-induced wing rock of slender wings［R］.AIAA paper 81-1883，1981.