均勻照明方形光斑的LED自由曲面透鏡設計
張 康,蘇成悅,王維江
(廣東工業大學 物理與光電工程學院,廣東 廣州 510006)
1 引言
LED由于其壽命長、能耗低等優點,在各個領域得到了廣泛的應用,如道路照明、投影機以及室內照明等[1]。但是由于LED光源發出的光近似朗伯型,發散角度比較大,這就需要對LED光源進行二次配光設計,來滿足目標照明面的要求[2~3]。
目前自由曲面的求解方法主要有:剪裁法、劃分網格法和SMS法。Ries等人提出了剪裁法,其基本思想是根據目標面的照度分布和光源特性建立一個關于光學面形的非線性偏微分方程組,通過解這個微分方程組得到光學面形[4~6]。丁毅等提出了基于偏微分方程組數值求解法得到了用于均勻照明的自由曲面透鏡和反射器[7~8]。蔣金波等提出基于光學擴展量守恒的LED路燈透鏡設計[9]。劃分網格法的基本思路是根據邊緣光線理論,通過求解能量守恒方程,得到光源每個小網格與目標平面每個小網格能量的對應關系,最后,通過斯涅耳定律構造自由曲面。王洪等人利用劃分網格法得到了矩形光斑的自由曲面透鏡和反射器[10]。王愷等人提出非圓對稱自由曲面透鏡的算法[11]。上述方法都是針對點光源,當光源尺寸較大時,目標面的光斑會出現較大的惡化。SMS法針對擴展光源設計,可同時設計透鏡的多個表面,從而控制光源發出的兩個波面,變換成給定的兩個輸出波面,但是這種方法求解比較繁瑣,設計難度大。
本文以非成像光學原理為基礎,利用劃分網格的方法,在特定的坐標系內建立光源面與目標面網格的對應關系,設計了一種適用于大功率LED均勻照明的自由曲面透鏡,該透鏡實現了方形區域的均勻照明,并且當LED光源尺寸較大時,仍然能保持較高的能量利用率和照度均勻性,特別適用于投影顯示和道路照明等領域。隨著光源模組的應用推廣,通過對形成方形光斑光源模組的拼接,可投射出各種矩形光斑,能應用于各種照明領域,因此對方形光斑的研究有較強的理論和應用價值。
2 設計原理
根據邊緣光線理論,采用劃分網格的方法設計自由曲面透鏡。設計思路如下:首先建立LED光源與方形目標平面的能量對應關系;然后計算自由曲面透鏡上的點坐標和法相矢量,得到自由曲面面形。
2.1 網格劃分
根據光源與目標面的特點,對于光源選取空間球坐標系,網格劃分如圖1所示,對于目標面選取直角坐標系,網格劃分如圖2所示。光源位于坐標原點O,主光軸為z軸,沿著z軸方向的中心光強為I0,θ為光線與z軸的夾角,φ為光線在xoy平面內的投影與x軸的夾角。則光源發出的整體光通量為:

(1)
式中I(θ)=I0cos(θ)。

圖1 光源網格劃分Fig.1 Grid division of light source

圖2 目標平面網格劃分Fig.2 Grid division of target plane
假設目標照明面的平均照度為Ev,該1/4方形區域的長和寬分別為a和b,中心線為AC,首先,將第一象限AB和AD等分為m份,將方形的中心線AC劃分成n等分,這樣就形成了2m×n個三角形。對應光源面,則是在φ角上分成2m份,θ角上分成n份。
根據能量守恒原理可得:
(2)
根據式(2),就可以求出一系列的θ值。同樣,根據能量守恒有:

(3)
根據式(3)即可求得一系列的φ值。
2.2 構造自由曲面透鏡
如圖3所示,根據光源和目標照明面的能量對應關系在光源上選擇一條初始光線I0,經自由曲面折射后對應于目標照明面上的初始位置Q0,我們選取P0(0,0,z0)作為光學表面面型頂點作為計算的初始點,光源位于坐標原點。由這兩點坐標可求出初始光線入射光方向的單位矢量In和折射光方向的單位矢量Out,再由折射定律的矢量公式可求出自由曲面在初始點處的單位法矢量N為
(4)
式中n——自由曲面介質的折射率。

圖3 自由曲面透鏡表面生成示意圖Fig.3 Sketch of generating freeform lens surface
由法矢量和初始點坐標可求出過P0點的切平面T0。根據光源和目標照明面的能量對應關系,在光源上選擇第二條出射光線I11,經自由曲面折射后對應于目標照明面上的點Q11,光線I11與切平面T0的交點P11(x1,0,z1),由這兩點坐標可求出光線I11入射光方向的單位矢量In11和折射光方向的單位矢量Out11,再由折射定律的矢量公式可求出自由曲面在P11點處的單位法矢量N11,按照上面的方法迭代,以此類推,依次求出P12到P1n,這樣就可以得到第一條初始曲線。第二條曲線的頂點仍然是P0,與第一條曲線構造方法不同的是,第二條曲線上的第二點P21為相應的入射光線I21與前一條曲線上點P11的切平面的交點。按照求解一條曲線的方法,可以依次求出P21到P2n。在上述曲線構造過程中,P2i的真實法線方向與計算得出的法線方向存在一定的誤差,保證誤差角度小于5°,否則刪除該條曲線,并重新計算初始曲線。按照上述方法,依次類推可以求得第三條直至第2M條曲線。
3 模擬與分析
為簡化模型,所求透鏡的內表面為半球面,LED位于坐標原點,LED發出的光線透過該內表面不發生偏折,透鏡外表面即為自由曲面。假設透鏡所用材料為PMMA,折射率為1.49,且光線通過時無損耗,即系統能量守恒。
實例設計:設計實現10m×10m正方形區域均勻照明。選取初始點坐標P0(0,0,10),即取透鏡高度為10mm;光源距離目標面的距離H=3m。通過上述原理編程計算,求得離散的數據點,再將離散點導入到三維建模軟件中,通過放樣擬合成曲面,最后生成實體如圖4所示,透鏡縱向最大長度為11mm,橫向最大長度為24mm。將該透鏡導入到tracepro中,選取光源的尺寸為1mm×1mm進行光線追跡,光線數目為100萬,模擬的光強分布圖如圖5所示,目標面照度圖如圖6所示。

圖4 透鏡三維模型圖Fig.4 3D model of the lens

圖5 極坐標光強分布圖Fig.5 Polar Candela Distribution plot
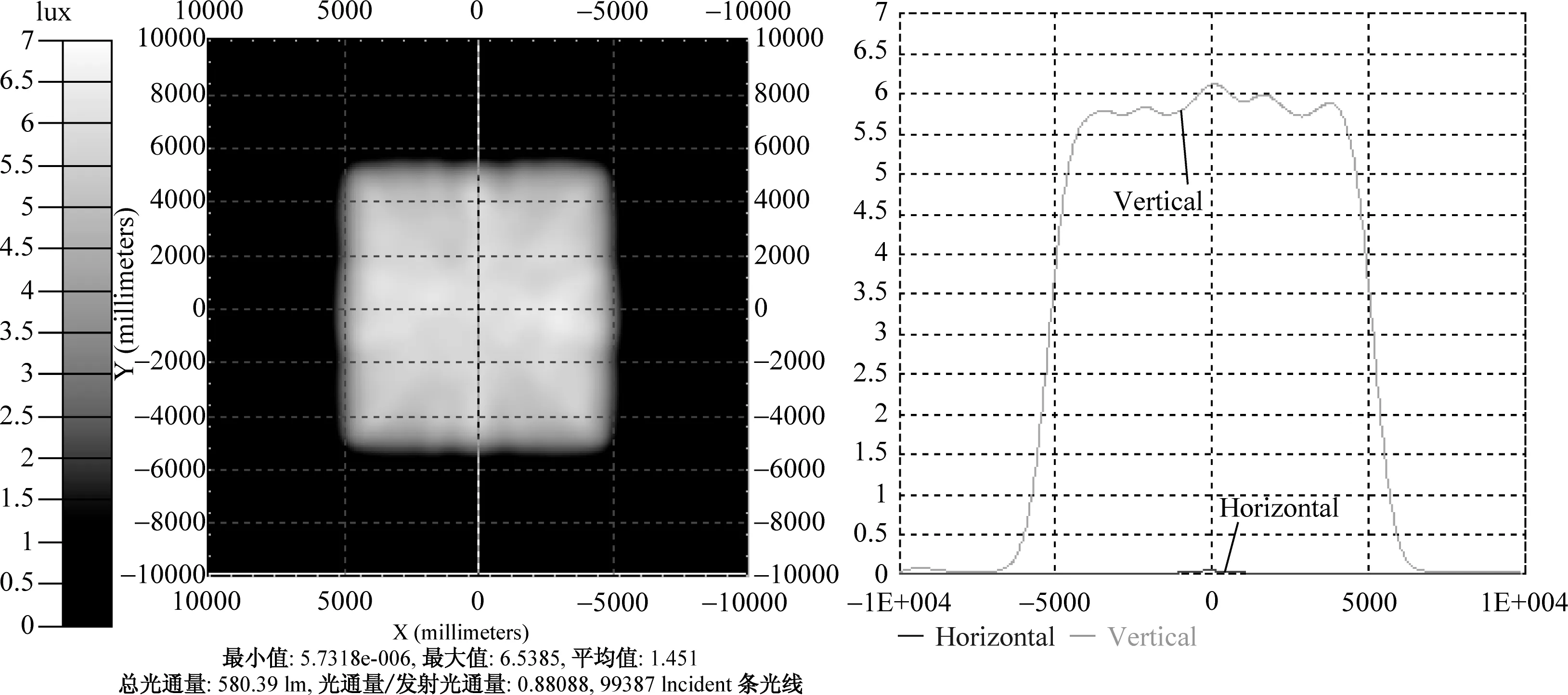
圖6 光源為1mm×1mm的照度圖Fig.6 Illuminance map of 1mm×1mm source
為了更好的評價均勻照度透鏡的性能,借鑒照度中的平臺均勻度的概念,我們重新明確了照度平臺均勻度的含義。即在照度曲線分布圖中,平臺段內的照度分布曲線的多個峰谷中,這些峰谷的最小照度和最大照度之比,即U=Emin/Emax,其值表征了平臺區域內照度分布的均勻性,這里我們選擇了其中一個方向進行討論。從照度圖中我們可以看出,目標面的照度均勻性為90%,系統光能利用率為88.2%,LED光強分布為蝙蝠翼配光。在距離光源不同的高度H處設置接收面,H變化時接收面上的能量利用率基本不受影響,均勻性略微有一點波動,可見系統的效率基本不受接收面高度H的影響。下面我們通過仿真的方法來討論光源的尺寸變化對系統的影響,并確認了這款透鏡適用于擴展光源配光。
3.1 光源尺寸對系統的影響
在其他條件不變的情況下,增大LED光源的尺寸,分析其配光效果以及LED尺寸對配光效果的影響。下面是光源尺寸為2mm×2mm,3mm×3mm,4mm×4mm,5mm×5mm的照度圖,如圖7~圖10所示。根據上面的照度圖,我們可以得到表1中的照度均勻度和能量利用率。
從表1數據我們可以看出:當光源尺寸增大時,接收面的能量利用率基本保持不變,而目標面的照度均勻性略有降低,但仍處于較高的水平。當光源尺寸與透鏡高度尺寸之比為3∶10,1∶2.5,1∶2時,該比例已超過1∶5,可以理解為擴展光源的情況,目標面的照度均勻度都在80%以上,均勻性較高,這說明該透鏡對一定尺寸比例的擴展光源仍然適用。

圖7 光源為2mm×2mm的照度圖Fig.7 Illuminance map of 2mm×2mm source

圖8 光源為3mm×3mm的照度圖Fig.8 Illuminance map of 3mm×3mm source

圖9 光源為4mm×4mm的照度圖Fig.9 Illuminance map of 4mm×4mm source

圖10 光源為5mm×5mm的照度圖Fig.10 Illuminance map of 5mm×5mm source

表1 光源尺寸對系統的影響Table 1 Influence of LED’s size on the system
3.2 光源尺寸為10mm×10mm的配光
針對更大尺寸的擴展光源,比如為10mm×10mm,如果仍使用上述透鏡進行配光,此時光源尺寸與透鏡尺寸之比為1∶1,仿真結果如圖11所示,目標面的照度均勻光斑區域減小,只在約6mm×6mm的區域內保持較好的照度均勻性,邊緣過渡區域變大。對于這種情況,可以通過對透鏡高度的調整和優化來保證10mm×10mm區域內的照度均勻性,以達到設計要求。選取初始點坐標P0(0,0,20),即取透鏡高度為20mm,重新按上述過程編程計算,建模仿真后,其照度圖如圖12所示,此時目標面均勻照度區域變大,照度均勻度為86%,照明效果得到了明顯的改善。由此可見對于集成LED光源可以通過增大透鏡的尺寸來完成配光,實現均勻照明的效果。

圖11 透鏡高度為10mm,光源為10mm×10mm的照度圖Fig.11 Lens height is 10mm,illuminance map of 10mm×10mm source

圖12 透鏡高度為20mm,光源為10mm×10mm的照度圖Fig.12 Lens height is 20mm,illuminance map of 10mm×10mm source
4 結論
集成光源配光是目前研究的一個熱點,因為計算困難也是配光設計的一個難點。本文根據邊緣光線理論,選用劃分網格法求解自由曲面,設計出針對集成光源的可實現方形區域內均勻照明的自由曲面LED透鏡。光學仿真的結果表明:在透鏡大小不變的情況下,增大LED的尺寸,當LED光源尺寸與透鏡高度之比為1∶10和1∶5時,LED可被認為是點光源,目標面的照度均勻度高達90%,透鏡的能量利用率為88%,這說明設計的透鏡對點光源有較好的光學配光性能。當LED光源尺寸與透鏡高度之比為3∶10等大于1∶5比例時,LED可被認為是擴展光源,目標面的照度均勻性有所降低,但均勻度在80%以上,仍然處于較高的水平,透鏡的能量利用率在88%左右,基本保持不變,這說明該透鏡對一定尺寸的擴展光源仍然適用。特別是當LED光源尺寸與透鏡高度之比為1∶1時,照明區域均勻光斑區域變小,但通過優化透鏡高度仍能達到設定的均勻照明區,獲得理想的均勻照度。由于本方法設計的透鏡可應用于LED集成光源,有較好的配光性能,適用于投影照明和室內外照明等領域,應用前景廣闊。
[1] 史永勝,買迪,寧磊. 實現道路均勻照明的LED自由曲面透鏡設計方法綜述[J].照明工程學報,2010,21(5):73~77.
[2] 劉正權,孫耀杰,林燕丹.基于LED的自由曲面反射器設計軟件研究[J].照明工程學報,2012,23(4):56~60.
[3] 周鎮,蘇成悅,付倩,等.一種基于自由曲面的LED準直透鏡設計[J].應用光學, 2012,33(6):1058~1062.
[4] Ries H,Muschaweck J. Tailoring freeform lenses for illuminations[J]. SPIE, 2001,4442: 43~ 50.
[5] Ries H,Muschaweck J. Tailored freeform optical surfaces[J]. J. Opt. Soc. Am. A, 2002, 19(3): 590~ 595.
[6] Timinger A,Muschaweck J,Ries H. Designing tailored freeform surfaces for general illumination[J]. SPIE,2003,5186: 28~ 32.
[7] Ding Y,Liu X,Zheng ZR,et al. Freeform LED lens for uniform illumination[J]. Opt. Express, 2008,16(17):12958~ 12966.
[8] 丁毅,顧培夫. 實現均勻照明的自由曲面反射器[J].光學學報,2007,27(3): 540~544.
[9] 蔣金波,杜雪,李榮彬. LED路燈透鏡的二次光學設計簡介[J]. 照明工程學報,2008,19(4): 59~65.
[10] 王洪,張奇輝,張小凡,等. 實現道路均勻照明的自由曲面反射器設計[J].光電工程,2009,36(12):143~66.
[11] 王愷.大功率LED封裝與應用的自由曲面光學研究[D]. 武漢:華中科技大學,2011.

