吊環對商用車前少片簧懸架性能的影響

劉兆英，李躍偉，洪 良

（中國第一汽車集團股份有限公司技術中心，長春130011）

懸架剛度及運動特性對汽車操縱穩定性以及平順性有重要的影響［1－2］。對前懸架采用少片簧的商用車而言，吊環長度和基礎吊環角的合理設計將影響到汽車的行駛性能［3］。目前國內各主機廠對于該類型懸架系統的設計還基本停留在板簧的應力和剛度計算階段；國外部分樣車為了提高制動時懸架系統的性能，增加了防S變形［3－4］緩沖塊，而制動時板簧的運動特性還未見報道。目前關于吊環的布置與懸架性能的匹配仍依賴于設計人員的經驗，缺乏相關的計算理論依據。本文擬建立商用車前少片簧懸架系統的有限元分析模型（Finite element analysis，FEA），采用仿真方法研究了吊環長度和基礎吊環角對懸架剛度和運動特性的影響規律；結合試驗結果，驗證了仿真方法以及結果的正確性，并最終形成了設計可參考使用的結論。

1 考慮吊環布置的前少片簧懸架有限元模型

本文研究的某商用車前少片簧懸架系統布置如圖1（a）所示，該懸架系統布置特點描述如下：彈性元件為對稱的兩片少片鋼板彈簧；鋼板彈簧前端采用銷軸與支架連接，后端通過銷軸與吊環連接；吊環通過銷軸與后支架連接。上跳限位采用橡膠緩沖塊，通過減振器進行振動衰減。本次仿真模型不包括減振器以及緩沖塊。

采用Proe建立的少片簧幾何模型如圖1（b）所示，進而采用Hypermesh進行有限元網格三維前處理，鋼板彈簧采用六面體C3D8R進行建模［3，5－11］，如圖1（c）所示；并采用Abaqus軟件進行分析求解。根據上述方法計算得到的某商用車前少片簧自由和夾緊狀態剛度曲線如圖2所示。

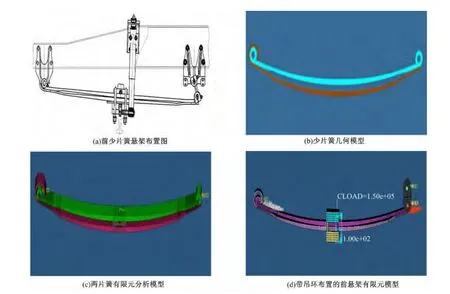
圖1 考慮吊環布置的前少片簧懸架有限元模型Fig.1 FEA model of front taper-leaf suspension system with hinger

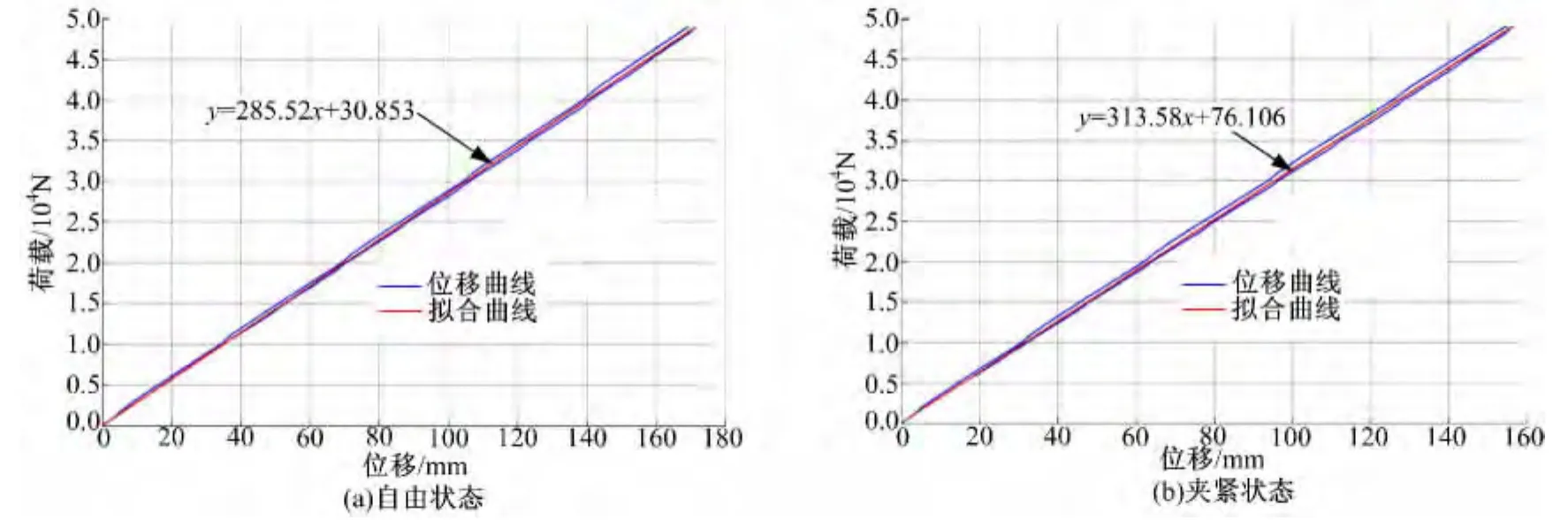
圖2 自由剛度及夾緊剛度模擬Fig.2 Simulation of free stiffness and clamped stiffness

表1給出了基于有限元計算得到的剛度擬合值與試驗值對比結果。可見兩者存在一定的誤差，但誤差在可接受范圍之內，目前板簧的剛度誤差要求在±7%之內。綜合上述對比結果及分析，該鋼板彈簧模型可以應用于系統分析。

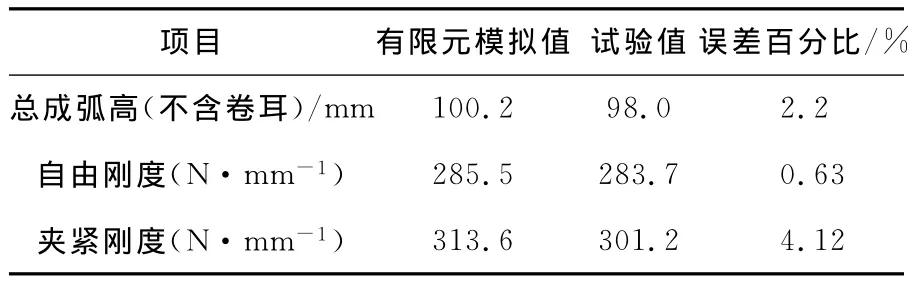
表1 有限元模擬結果與理論計算值Table 1 FEA results and theoretical calculation values

本次懸架系統分析主要是分析吊環的布置對懸架剛度的影響，所以前懸架系統主要包括如下部件：鋼板彈簧、吊環、U形螺栓以及上、下蓋板。為了方便有限元模擬，在自由狀態將兩個卷耳中心的連線設為水平。同時，為了方便對比結果，須引入以下定義：

基準線：對于帶有卷耳的鋼板彈簧總成來說，基準線是指通過兩個卷耳中心的連線；對于兩端無卷耳的鋼板彈簧總成，基準線是指通過總成端部的外載荷作用點的連線。

基準吊環角：是指當鋼板彈簧第一片為平直狀態時，基準線與吊環兩個連接孔的連線所形成的夾角。具體的有限元模型如圖1（d）所示。

2 吊環對懸架系統剛度的影響

為了更好地做對比分析，本次模擬主要分以下兩種情況［12－14］：①僅吊環長度l發生變化，分別取l為100 mm和180 mm，板簧長度為1700 mm。吊環長度與板簧長度比值近似為6%和10.5%；②僅基準吊環角θ發生變化，分別取60°、100°。

為了直觀，模擬的曲線橫坐標為輪胎跳動量與板簧長度的比值，其中“0”位置為板簧第一片為平直狀態時的輪心位置，正值代表上跳，負值代表下跳。前懸架系統自由及加載狀態下的FEA模型見圖3和圖4。

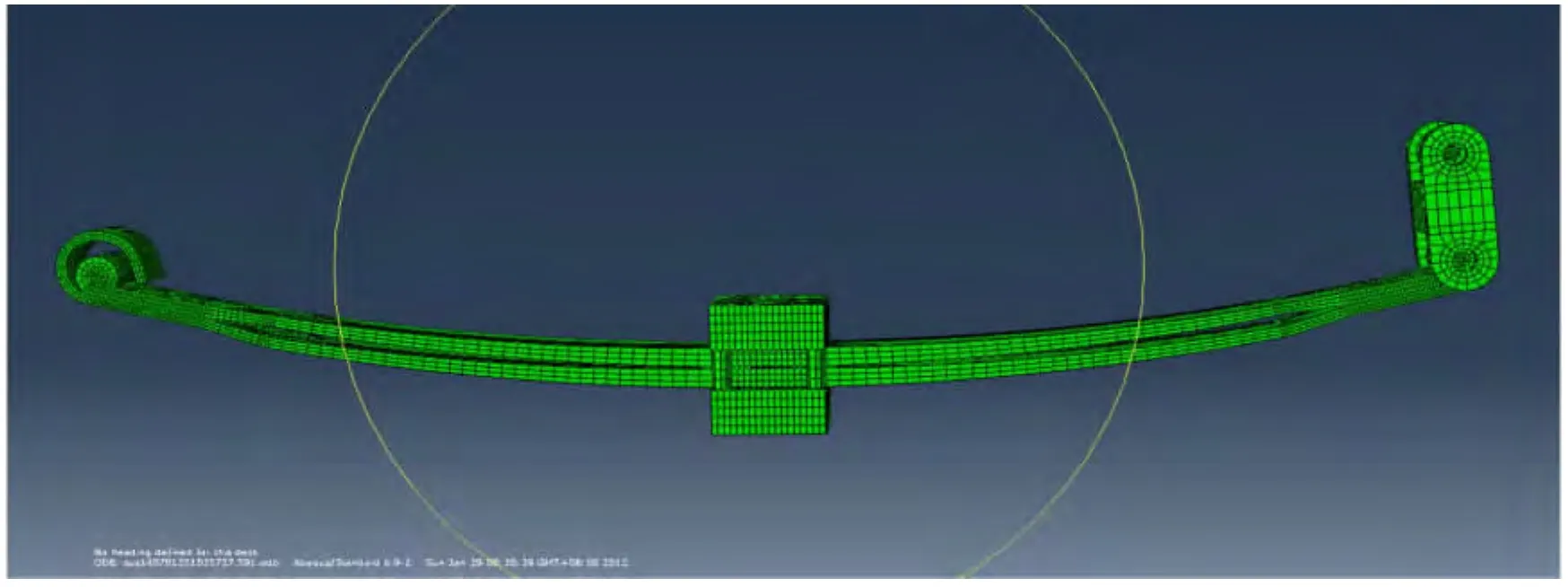
圖3 前懸架系統自由狀態Fig.3 Free situation of front suspension system

圖4 前懸架系統加載后狀態Fig.4 Loaded situation of front suspension system

由圖5及表2中的分析結果可見：懸架系統如果布置不合理，會帶來懸架系統性能的惡化，在懸架系統設計時應考慮吊環長度以及基礎吊環角的選擇；當l＝100 m，θ＝60°時，懸架系統剛度與板簧剛度差別較大；隨著車輪上跳，懸架剛度急劇增加；當θ增大到100°時，隨著車輪上跳，懸架剛度急劇下降，增加了限位塊碰撞的幾率。當吊環長度增加時，上述情況有所改善，但改善效果不明顯。

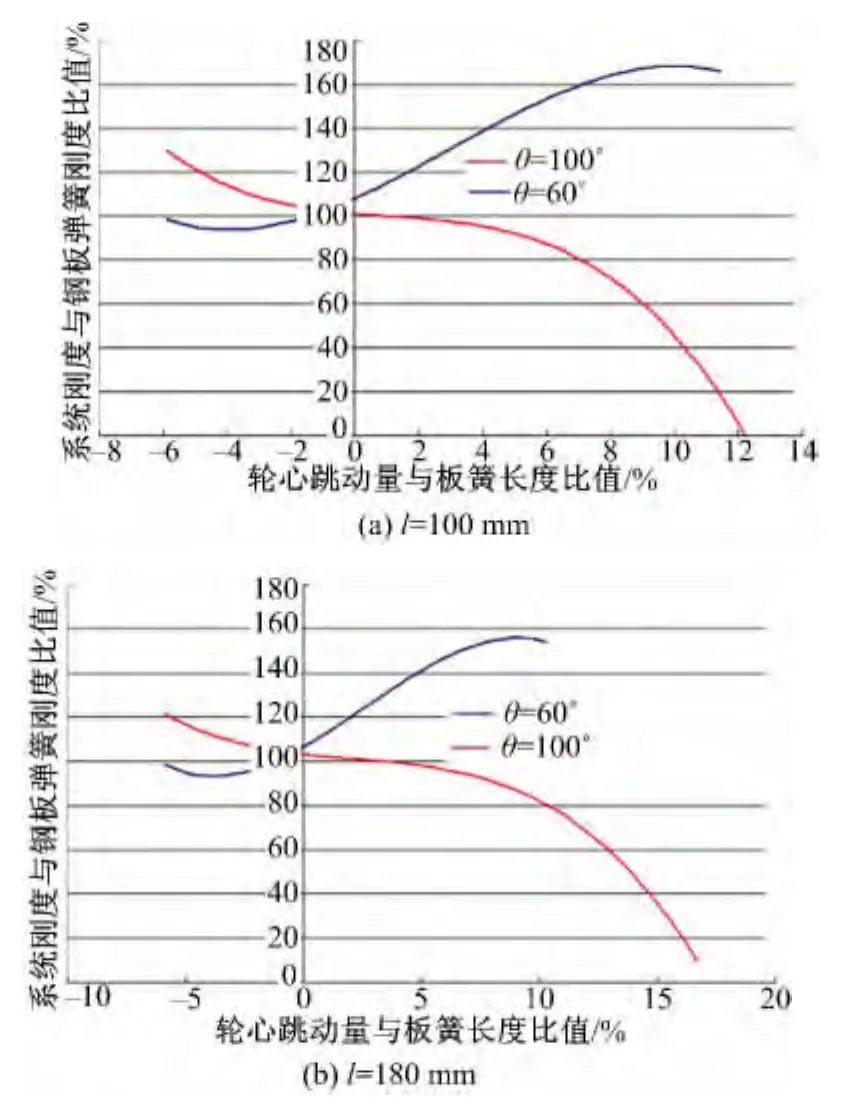
圖5 不同情況下懸架剛度變化曲線Fig.5 Curve of suspension stiffiness in different cases

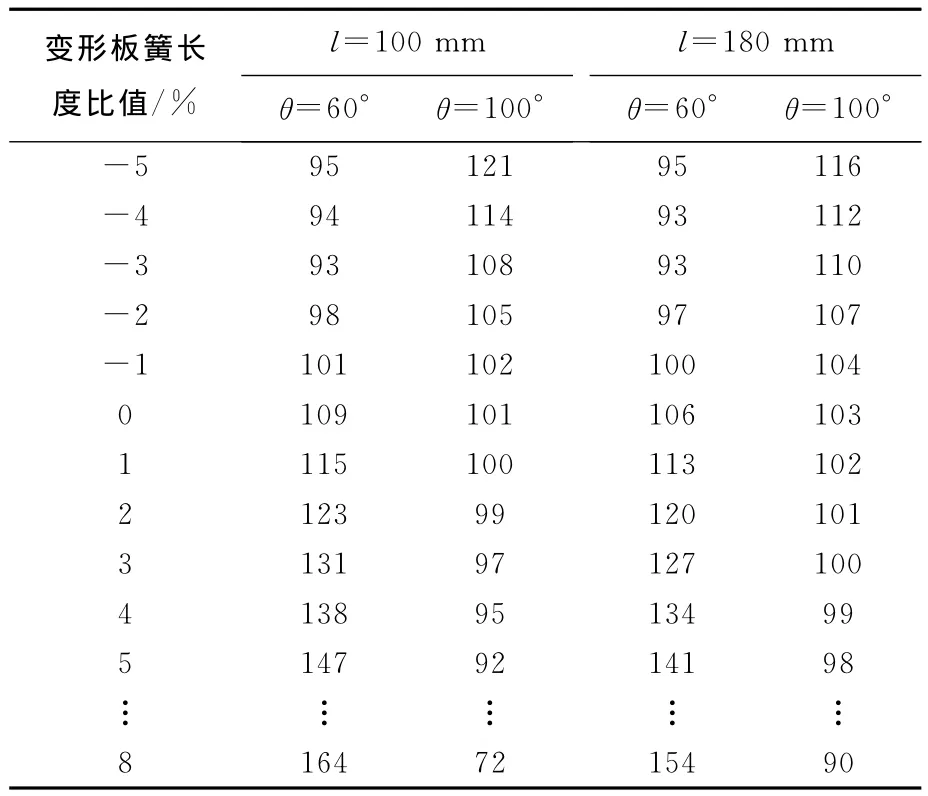
表2 懸架系統剛度與板簧剛度比值Table 2 Ratio of suspension system stiffness and spring stiffness

3 吊環對懸架系統運動的影響

3.1 吊環的擺動與板簧運動軌跡的關系

由圖6可見，隨著吊環長度的增加，車輪在上下跳動過程中，吊環的擺角減小；圖7表明吊環長度的變化對于前軸的運動軌跡幾乎沒有影響。

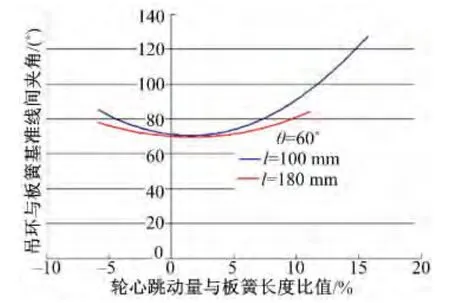
圖6 吊環角度隨車輪上跳變化曲線Fig.6 Hinger angle curve with wheel jump-up

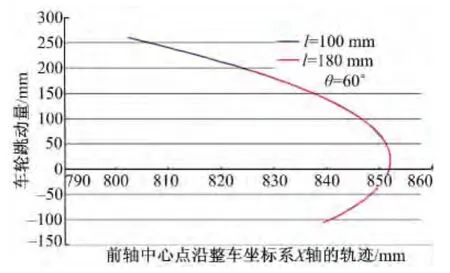
圖7 前軸軌跡Fig.7 Trail of front axle

3.2 制動時板簧的S變形與前軸轉角的關系

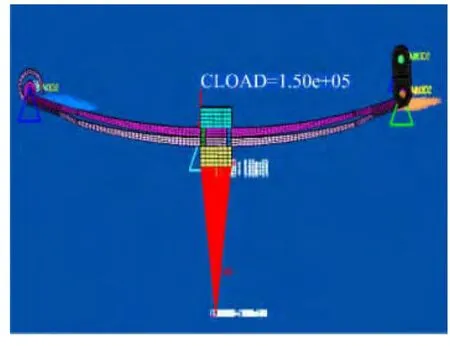
圖8為在Hypermesh中搭建制動工況下板簧S變形的分析模型。從圖9的分析結果可以看出，對于對稱板簧來說，車輪在上下跳動過程中，由于吊環的影響，前軸有很小的轉角，在垂直校核時可以忽略，這與目前的理論分析比較一致；在同樣的制動力情況下，理論計算前軸轉角為3.9°，與有限元結果比較一致，所以在后續設計過程中可以直接用試驗值進行初步校核；在制動時對于少片簧懸架來說，由于其剛度較小，由于S變形會導致懸架轉向干涉量以及板簧后半段應力提高，故在一些特殊條件下，需增加防S變形緩沖塊。

圖8 制動工況板簧S變形模擬分析Fig.8 S-shape deformation FEA of leaf-spring in brake case

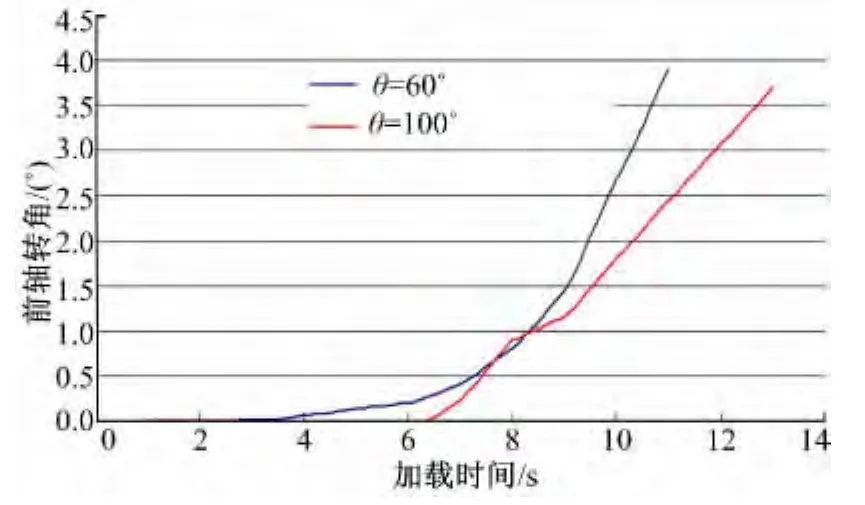
圖9 前軸轉角變化曲線Fig.9 Roation angle change curve of front axle

4 吊環布置與懸架剛度匹配試驗

為了驗證上述模擬分析結果以及結論的正確性，同時驗證上述結論是否對于其他長度的少片簧懸架系統同樣適用，采用了五十鈴中型車的前懸架系統進行臺架試驗，板簧長度為1300 mm，吊環長度為77 mm，吊環長度與板簧長度的比值為5.9%。臺架試驗圖見圖10，臺架試驗與有限元分析模擬的對比結果見圖11和表3。上述數據表明有限元模擬結果與臺架試驗結果一致性良好，驗證了本文方法的正確性。

圖10 五十鈴前懸架系統臺架試驗圖Fig.10 Photo of ISUZU front suspension bench test

圖11 臺架試驗與模擬結果對比Fig.11 Comparison between bench test and FEA result

表3 懸架剛度與板簧剛度的比值Table 3 Ratio of suspension system stiffness and spring stiffness

5 結 論

（1）本文在國內首次采用了FEA方法對商用車用前少片簧懸架系統的匹配進行了研究；驗證了該方法的可行性以及有效性。

（2）通過模擬分析，給出了懸架剛度隨吊環長度以及基礎吊環角變化的一般規律。

（3）利用前少片簧懸架系統的FEA模型進行了運動特性的模擬，掌握了前軸隨車輪上跳的運動規律，對懸架系統的校核具有一定的指導意義。

（4）搭建了帶有吊環的系統試驗臺，驗證了模擬分析結果的正確性。

［1］余志生.汽車理論［M］.北京：機械工業出版社，2000.

［2］劉惟信.汽車設計［M］.北京：清華大學出版社，2001.

［3］SAE Spring Committee.Spring Design Manual［M］. New York：Society of Automotive Engineers，Inc，1996.

［4］郭孔輝.汽車操縱動力學［M］.長春：吉林科學技術出版社，1991.

［5］Bittencourt E，Creus G J.Finite element analysis of three-dimensional contact and impact in large deformation problems［J］.Comput Struct，1998（69）：219-234.

［6］Pradade U，Medepalli S，Moore D，et al.Beam element leaf spring suspension model development and assessment using road load data［C］∥SAE Paper，2006-01-0994.

［7］Kirby D，Charniga R.A finite element and experimental analysis of a light truck leaf-spring system subjected to pre-tension and twist loads［C］∥SAE Paper，2005-01-3568.

［8］Jayakumar P，Alanoly J，Johnson R.Three-link leaf-spring model for road loads［C］∥SAE Paper，2005-01-0625.

［9］Yong J Y.Frictional behavior of automotive leaf spring［C］∥Proceedings of the 4th Korea，Russia International Symposium on Science and Technology，2000：5-10.

［10］Nogueira F，Teixeira R，Ueda O，et al.Nonlinear finite element study of the windup geometry of a parabolic front suspension leaf spring［C］∥SAE Paper，2000-01-3279.

［11］ABAQUS user＇s manual.version 5.8.H.K.S［S］. 1999.

［12］于安和，桂良進，范子杰.鋼板彈簧剛度特性的有限元分析［J］.汽車技術，2007，27（2）：123-125.

Yu An-he，Gui Liang－jin，Fan Zi-jie.FEA on the stiffness of leaf spring［J］.Automobile Technnnology，2007，27（2）：123-125.

［13］Kumar M S.Static analysis and fatigue life prediction of steel and composite leaf spring for light passenger vehicles［J］.Journal of Scientific and Industrial Research，2007，66（2）：128-134.

［14］Sugiyanm H，Shabana A A.Development of nonlinear elastic leaf spring model for muhibody vehicle systems［J］.Computer Methods in Applied Mechanics and Engineering，2006，195：50-51.