連續配筋混凝土路面力學行為的溫度效應

鐘春玲，李 娜，孟廣偉

（1.吉林建筑大學，長春130118；2.吉林大學機械科學與工程學院，長春130022；3.中元國際（長春）高新建筑設計院有限公司，長春130000）

0 引 言

連續配筋混凝土路面（CRCP）是在路面縱向配置連續的鋼筋，中間不設橫向脹縮縫，與普通混凝土路面相比，其耐久性和整體性以及行車舒適性都較好，而且CRCP的養護維修費用小，在歐洲和美國被廣泛采用［1－2］。在CRCP的設計計算過程中，冬夏溫差產生的路面變形受到地基及連續鋼筋的約束，所以CRCP的溫度應力是造成路面破壞的主要因素［3－4］，它往往超過荷載應力成為路面設計的主要控制指標。

國內外學者對CRCP的溫度效應進行了研究，形成了設計規范，并給出了該類路面的設計指標［5－6］。設計規范存在一定的局限性，例如我國的設計規范不能考慮裂縫寬度等因素的影響，而AASHTO設計方法則是基于觀測數據得出的經驗公式。

對CRCP開裂情況的研究，國外學者主要采用現場觀測和加速加載試驗的方法［7－8］，缺乏深入的理論分析。同樣我國學者也對CRCP的裂縫發展情況進行了現場觀測［9］。在理論分析方面，國內學者典型的研究成果為以兩條相鄰裂縫之間的路段為研究對象，假定裂縫處鋼筋的位移為零，推導了CRCP在季節性溫差作用下受力性能［10－11］。然而在實際工程中，裂縫處鋼筋的位移并不為零，使得各裂縫間隔段存在耦合，從而導致現有的理論求解模型在端部區域存在較大誤差。

為了解決上述問題，基于有限元方法的基本理論，建立了連續配筋混凝土路面力學行為的溫度效應分析模型。該理論模型最大的特點是能夠考慮裂縫處鋼筋的實際位移當作約束條件，從而考慮各裂縫間隔段的耦合效應。此特點決定了用本文的理論分析模型可以精確計算出溫度作用下連續配筋混凝土路面整個路段各區段的靜力響應。

1 理論模型的建立

1.1 基本假定

如圖1所示，CRCP通常在端部設置錨固地梁來約束由于混凝土干縮和溫度變化引起的路面位移（見圖1（a））。也可以通過計算在端部設置橋梁用伸縮縫的方式滿足端部位移（見圖1（b））。因為在連續配筋混凝土路面中，鋼筋是等間距布置的，根據彈性力學基本原理可取出任意含一根鋼筋、寬度為一個鋼筋間距的板條進行分析。基本假定如下：①鋼筋和混凝土之間的粘結應力與兩者之間的位移差成正比；②地基摩阻應力與混凝土路面板的位移成正比；③假設混凝土路面板與地基始終不脫離［5］。

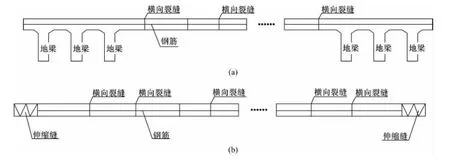
圖1 連續配筋混凝土路面Fig.1 Continuously reinforced concrete pavement

1.2 求解方程的形成

單元模型如圖2所示，路面在溫度應力作用下的位移包括混凝土路面板的軸向位移uc（x），鋼筋的軸向位移us（x）。混凝土路面板與連續鋼筋的粘結應力系數為ks，地基摩阻力系數為kc。

1.2.1 單元的位移模式

在連續配筋混凝土路面中，鋼筋位于路面的中性層位置，先給出鋼筋的位移模式對結構分析的影響，令鋼筋的縱向位移為

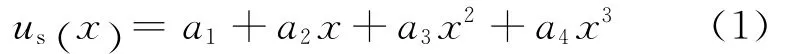
如圖3所示，根據微元體的受力平衡關系可得：

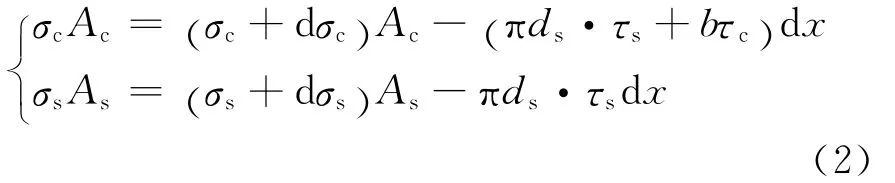
式中：As為鋼筋的橫斷面面積；Ac為混凝土板的截面積；ds為鋼筋直徑；b為混凝土路面板的寬度；σs為鋼筋應力；σc為混凝土應力；τs為鋼筋與混凝土之間的粘結應力；τc為混凝土路面板與地基之間的摩阻應力。

圖2 單元結點位移Fig.2 Node displacement of element

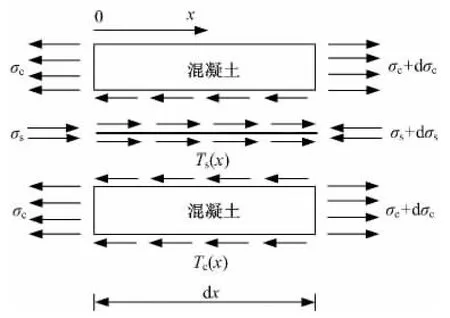
圖3 微元體Fig.3 Micro-unit

由式（2）可知：

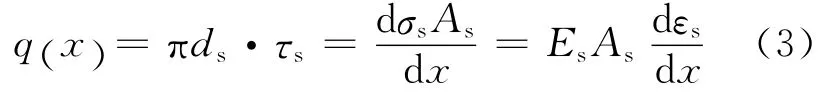
式中：εs為鋼筋的應變；Es為鋼筋的彈性模量；Ec為混凝土的彈性模量。

由材料力學可知：

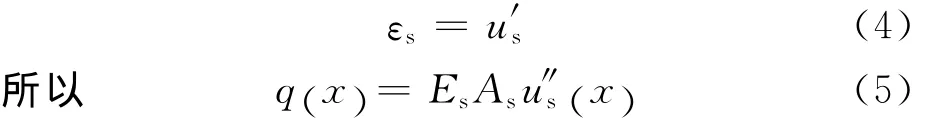
由基本假定可知：

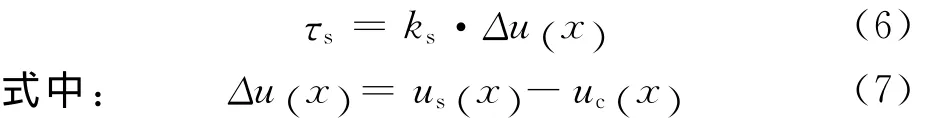
根據式（1）（3）（5）（6）可得：

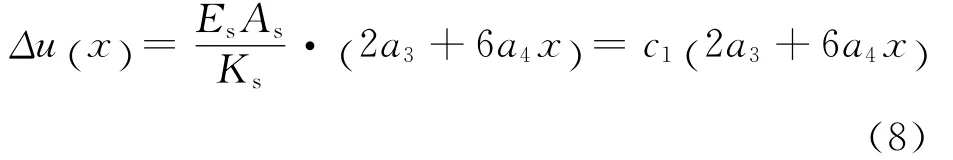
式中：c1＝（EsAs）／Ks，Ks＝ks·∑πds。

由式（1）（7）（8）可得：

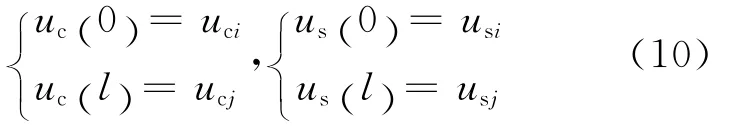
將式（10）代入式（1）和式（9）可得

寫成矩陣形式為

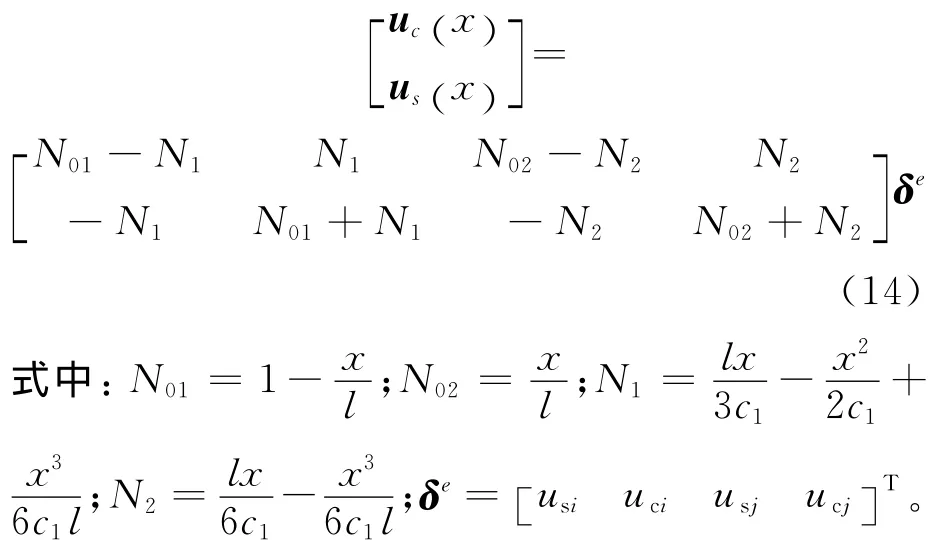
1.2.2 單元的幾何方程

令混凝土路面板和連續鋼筋的應變分別為εc（x）、εs（x）。根據式（4）和彈性力學的基本原理可知，單元上任意點的應變可表示如下：

式中：B為應變矩陣：

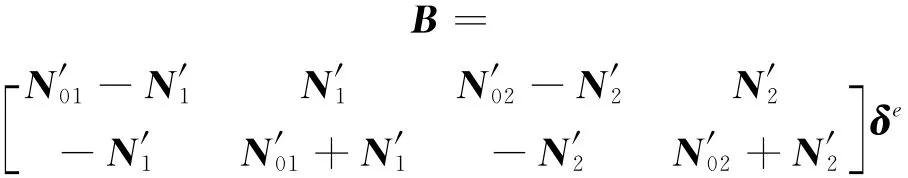
根據式（7）（8）可知連續鋼筋與混凝土路面板之間的滑移量為

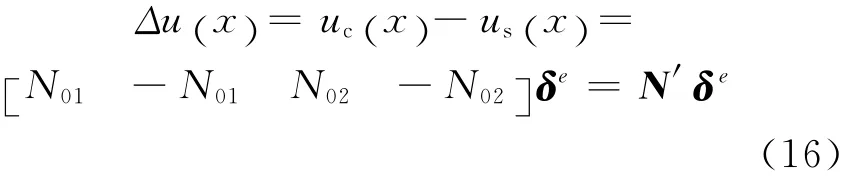
1.2.3 單元的物理方程

2.1.2拯救瀕危物種加快實施中華鱘、長江鱘、長江江豚等長江珍稀水生生物拯救行動計劃，建立完善的自然種群監測、評估與預警體系。在三峽水庫、長江故道、河口、近海等水域建設一批中華鱘接力保種基地。制定中華鱘規模化增殖放流規劃。在長江中下游夾江、故道、水庫、湖泊等水域建設一批長江江豚遷地保護水域。支持有條件的科研單位和水族館建設長江珍稀瀕危物種人工繁育和科普教育基地。

（1）應力與應變的關系

根據彈性力學的基本原理，路面單元的節點力列陣可表示為

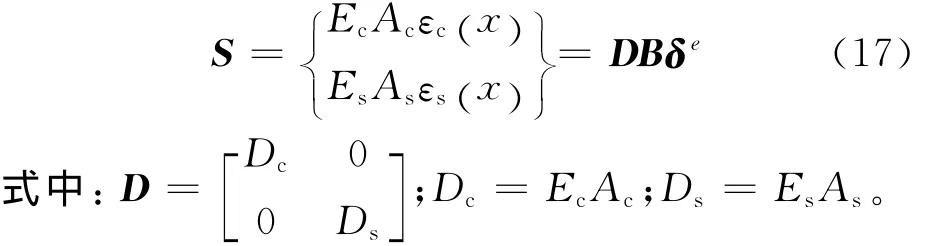
（2）鋼筋與混凝土之間的粘結力與滑移量之間的關系

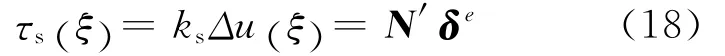
（3）混凝土的位移與地基摩阻力之間的關系

假定在一個單元內地基摩阻力與混凝土路面的位移之間的關系為線性，則地基應力為

式中：

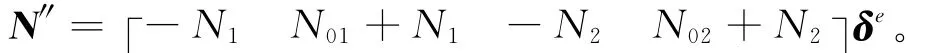
1.2.4 單元的剛度方程

設單元結點力列陣為

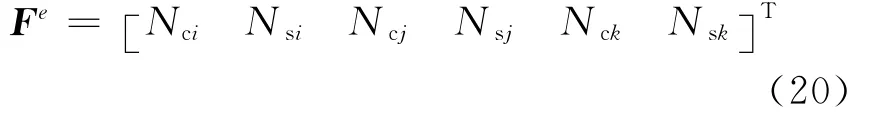
則單元的總勢能為

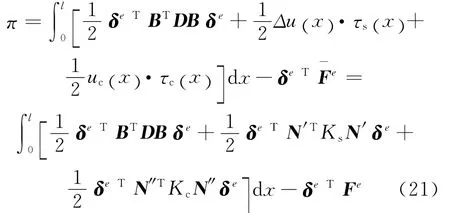
式中：Kc＝kcb。

根據最小勢能原理，對系統的勢能函數π取一階變分，并令π的一階變分為零：

由式（22）可得到路面部分的單元剛度方程為

2 算例分析

利用上述公式，分析了降溫30℃時（假設施工溫度為10℃，統計資料表明長春地區月平均最低氣溫為－20℃），圖4為一條1000 m長的CRCP的位移和應力狀態，其中板厚為25 cm，鋼筋間距為10 cm，ds＝14 mm，鋼筋和混凝土的線膨脹系數α＝1.0×10－5，kc＝4 kPa／mm，Ec＝3.25×107k Pa，Es＝2.1×108k Pa，ks＝50×103kPa／mm。CRCP中鋼筋和混凝土的位移計算結果如圖5～圖7所示。

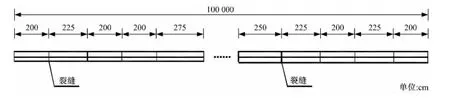
圖4 CRCP裂縫分布圖Fig.4 Crack distribute of CRCP

圖5給出的是全路段鋼筋和混凝土路面板的位移狀態，圖6給出的是路段坐標0～8 m范圍內的鋼筋和混凝土路面板的位移狀態，圖7給出的是路段坐標496～504 m范圍內的鋼筋和混凝土路面板的位移狀態。根據圖4給出的裂縫分布情況，可知路段在坐標為2 m、4.25 m、6.25 m處均存在裂縫，從圖6中可以看出，裂縫處的鋼筋位移不等于零，圖7中混凝土位移有突變的位置即為裂縫存在的位置。從圖6和圖7中可以，看出在降溫作用下CRCP的鋼筋位移不等于零，但是在路面的中段區域裂縫處的鋼筋位移較小。因此當端部設置的橋梁用伸縮縫時，應采用全路段聯合分析CRCP的位移和應力狀態。

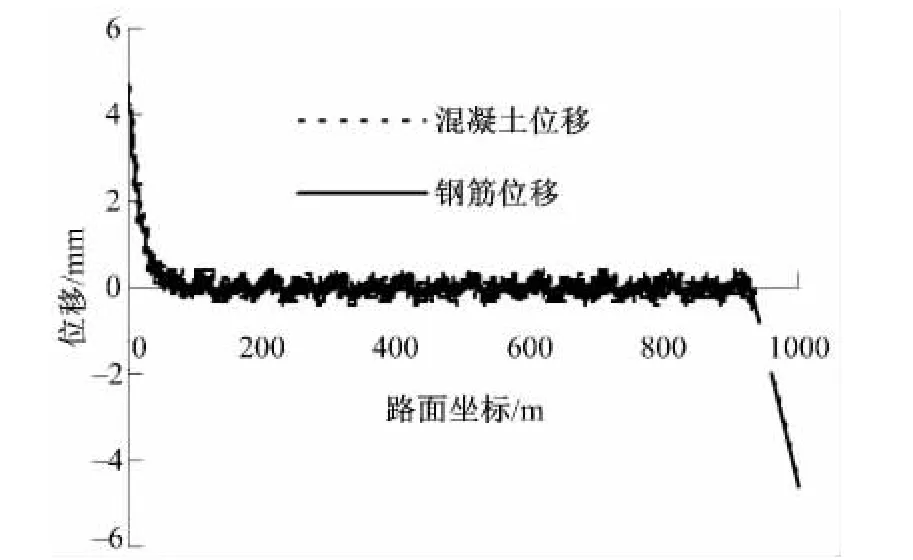
圖5 路面位移曲線Fig.5 Displacement curve of pavement

圖6 路面端部位移狀態Fig.6 Displacement magnifier of pavement end

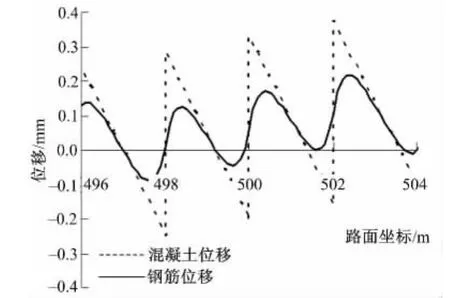
圖7 路面中段位移狀態Fig.7 Displacement magnifier of pavement mid

為了說明上述計算理論的合理性，利用本文推導的計算理論結合裂縫發展規律得到的裂縫平均間距和文獻［9］中的觀測結果進行了對比分析，如圖8所示，可以看出二者吻合得較好，說明利用本文的分析方法能夠較為精確地計算連續配筋混凝土路面在溫度作用下的位移狀態。

圖8 裂縫間距隨混凝土齡期的變化Fig.8 Crack spacing vs.age of concrete

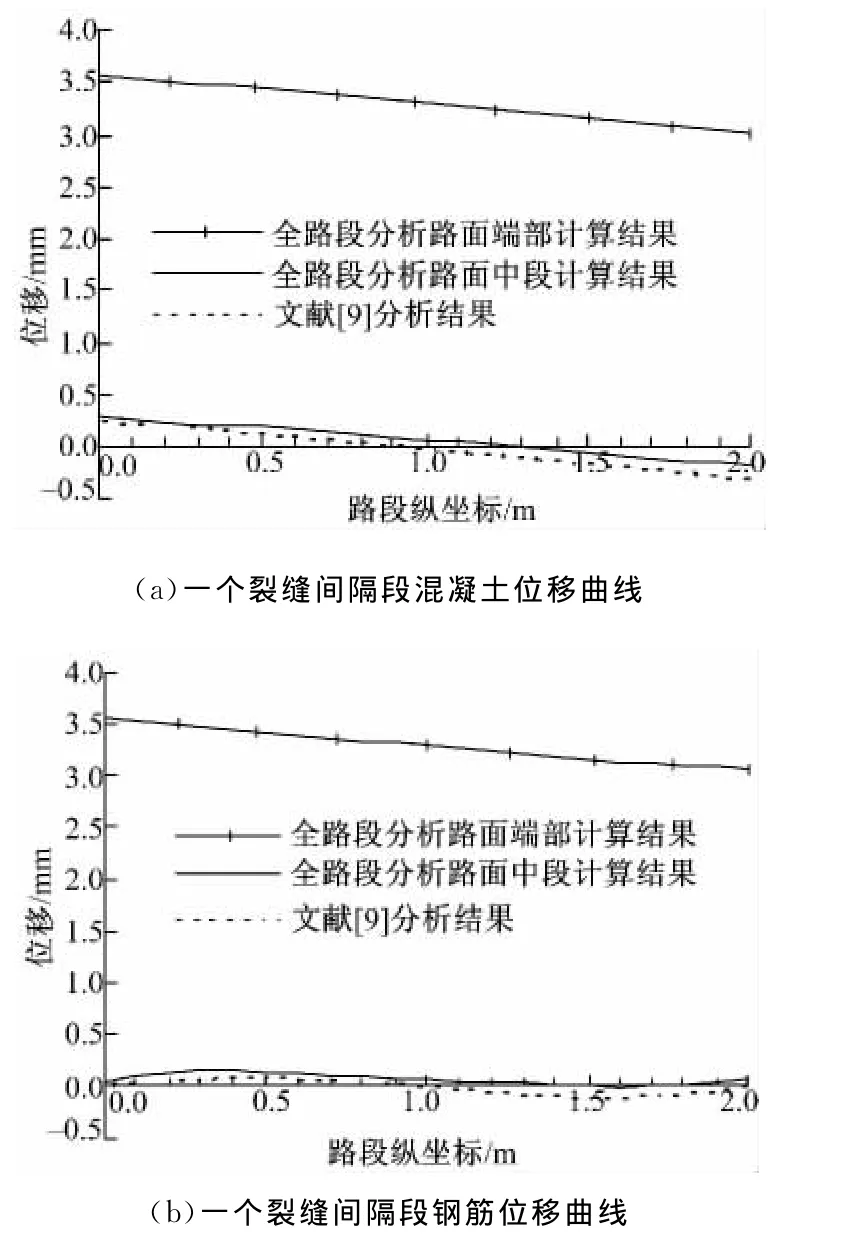
圖9 路面位移對比分析Fig.9 Comparative analysis of pavement displacement

目前對CRCP位移的計算大多采用文獻［11］給出的計算理論，該理論是取一個裂縫間隔段單獨分析，以裂縫處的鋼筋位移為零作為前提進行計算，由于忽略了各個裂縫間隔段的相互作用，會給計算結果帶來一定的誤差，本文計算理論考慮了路面全長內所有裂縫間隔段的聯合作用，更符合實際受力情況。二者的計算結果如圖9所示，可以看出：以某路段端部計算出的鋼筋和混凝土位移，均與以該路段中部計算出的相應位移存在一定差異，混凝土的位移最大相差20%左右，在道路的端部區域差別較大，說明本文給出的計算結果有較高的應用價值。

對于兩端設置伸縮縫的CRCP，其端部位移的計算是控制伸縮縫設置類型的關鍵，因此本文給出了不同地基摩阻力系數對端部位移的影響，如圖10所示。從圖10可以看出，地基摩阻力系數越大，端部位移越小，說明地基對路面板的約束越強，從控制端部位移的角度分析，地基摩阻力系數越大對結構越有利。

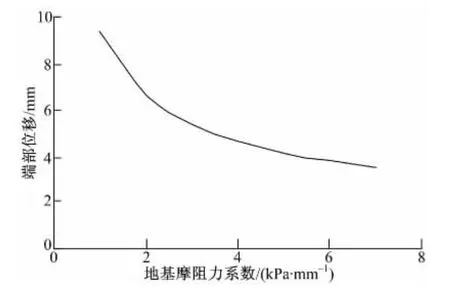
圖10 地基摩阻力系數與路面端部位移的關系Fig.10 Relatioship between subgrade friction and displacement of pavement end

3 結束語

基于有限元方法，建立了連續配筋混凝土路面力學行為的溫度效應分析模型。該模型最大的特點是能夠考慮裂縫處鋼筋位移的實際狀態，從而考慮各裂縫間隔段的耦合效應。采用數值模擬方法計算了溫度作用下連續配筋混凝土路面整個路段各區段的靜力響應，并與現有的計算理論進行了對比分析。結果表明本文給出的計算理論有較高的推廣應用價值。最后給出了設置伸縮縫的連續配筋混凝土路面端部位移與地基摩阻力系數的對應關系，為設置伸縮縫的允許寬度提供了理論依據。

［1］查旭東，王燕，韓春華.歐洲水泥混凝土路面綜述［J］.國外公路，1999，19（3）：16-22.

Zha Xu-dong，Wang Yan，Han Chun-hua.Summary of cement concrete pavement in Europe［J］.Journal of Foreign Highway，1999，19（3）：16-22.

［2］McCullough B F.Criteria for the design，construction and maintenance of continuously reinforced concrete pavement［J］.Australian Road Research， 1983，13（2）：79-99.

［3］陳云鶴，鄧學鈞，楊樹才，等.連續配筋混凝土路面早期裂縫寬度分析［J］.中國公路學報，1998，11（Sup）：36-42.

Chen Yun-he，Deng Xue-jun，Yang Shu-cai，et al. Analysis of crack width in continuously reinforced concrete pavement（CRCP）at early ages［J］.China Journal of Highway and Transport，1998，11（Sup）：36-42.

［4］陳鋒鋒，黃曉明，秦永春.連續配筋混凝土路面橫向裂縫分布模型的研究［J］.公路交通科技，2006，23（6）：18-21.

Chen Feng-feng，Huang Xiao-ming，Qin Yongchun.Study on the probability distribution model of continuously reinforce concrete pavement transverse cracks［J］.Journal of Highway and Transportation Research and Development，2006，23（6）：18-21.

［5］中華人民共和國交通部.公路水泥混凝土路面設計規范（JTG D40-2002）［S］.北京：人民交通出版社，2002.

［6］AASHTO.AASHTO Guide for Design of Pavement Structures［M］.Washington DC：AASHTO，1993.

［7］Kohler E，Roesler J.Crack spacing and crack width investigation from experimental CRCP sections［J］. International Journal of Pavement Engineering，2006，7（4）：331-340.

［8］Gharaibeh Nasir G，Darter Michael I，Heckel Laura B.Field performance of continuously reinforced concrete pavement in Illinois［C］∥Transportation Research Record，1999，1684：44-50.

［9］查旭東.連續配筋混凝土路面橫向開裂發展規律［J］.交通運輸工程學報，2008，8（2）：65-68.

Zha Xu-dong.Elastic solution for thermal stress in continuously reinforced concrete pavement（CROP）［J］.Chinese Journal of Applied Mechanics，2000，17（4）：36-42.

［10］曹東偉.連續配筋混凝土路面結構研究［D］.西安：長安大學，2001.

Cao Dong-wei.Research on structure of continuously reinforced concrete pavement［D］.Xi＇an：Chang＇an University，2001.

［11］曹東偉，胡長順.連續配筋混凝土路面溫度應力分析［J］.西安公路交通大學學報，2001，21（2）：1-5.

Cao Dong-wei，Hu Chang-shun.Analysis of the thermal stress for continuously reinforced concrete pavement（CRCP）［J］.Journal of Xi＇an Highway U-niversity，2001，21（2）：1-5.