CVT 插電式混合動力汽車全局優化控制策略

楊官龍，秦大同，劉永剛，林毓培

(重慶大學 機械傳動國家重點實驗室，重慶，400044)

控制策略對插電式混合動力電動汽車(PHEV)的能耗經濟性有著至關重要的影響，是插電式混合動力電動汽車的研究熱點之一。有關控制策略的優化方法有多種，其中等效消耗最小值控制策略(ECMS)和動態規劃(DP)算法得到廣泛的關注。Geng 等[1]采用極小值原理對ECMS 進行了求解，結果表明：ECMS 能較大的提高燃油經濟性；Chen 等[2]分別對ECMS 和DP 算法進行了研究，結果表明：DP 算法的優化效果更加明顯；Yang 等[3]采用DP 研究了道路坡度以及未來工況的劃分對能耗經濟性和排放的影響；Gong 等[4]采用DP 算法加強對PHEV 的電量消耗(CD)模式下電池荷電狀態(SOC)下降幅度的控制，有效地改善了車輛的能耗經濟性；張博等[5]應用DP 全局優化算法對PHEV在不同行駛里程下的控制策略進行了全局優化，得到動力總成在典型循環工況下的全局最優控制規律以及不同行駛里程下的最優控制規律；Moura 等[6-7]采用隨機動態算法對比研究了PHEV 電池SOC 軌跡為混合模式和電量消耗維持模式對電池容量和能耗經濟性的影響；Mojtaba 等[8]采用DP 算法研究了發動機冷熱起動對PHEV 能耗經濟性的影響；舒紅等[9]采用DP 算法研究了模型預測控制策略對燃油經濟性的影響。由文獻分析可知，諸多研究者采用了DP 算法對特定工況進行全局優化以最大限度的提高整車的能耗經濟性，但沒有對采用機械無級變速器(CVT)的插電式混合動力汽車進行過全局尋優，且由于DP 算法的計算時間較長，不適合控制策略的在線實時控制；因此，本文作者針對一款新設計的并聯式單電機CVT 插電式混合動力汽車，融合瞬時優化和DP 全局優化相結合的算法對PHEV 進行了優化研究，得到特定工況下的最優控制規律；并針對DP 算法無法用于在線實時控制的缺陷，采用誤差反向傳播(BP)神經網絡對發動機與電機工作點進行擬合，提煉出適用于道路循環工況的控制策略規則。

1 PHEV 動力系統模型

1.1 PHEV 動力系統介紹

PHEV 動力系統由發動機、ISG(Integrated Starter/Generator)電機、單向離合器C1(用來保證傳動系統的轉速不低于發動機的轉速)、摩擦離合器C2(用于ISG 電機啟動發動機及傳遞發動機轉矩)、CVT、差速器、電池組等部件組成，其構成如圖1 所示。

1.2 PHEV 動力系統建模

根據圖1 可以得到動力總成部件之間的動力學關系：

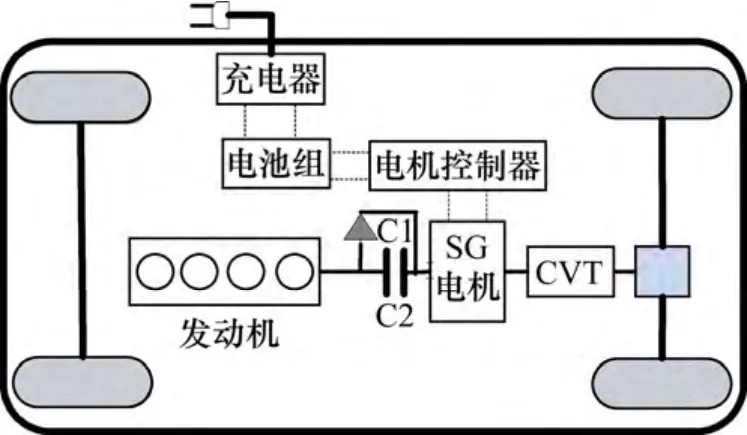
圖1 單電機PHEV 動力系統Fig.1 Powertrain of single motor PHEV

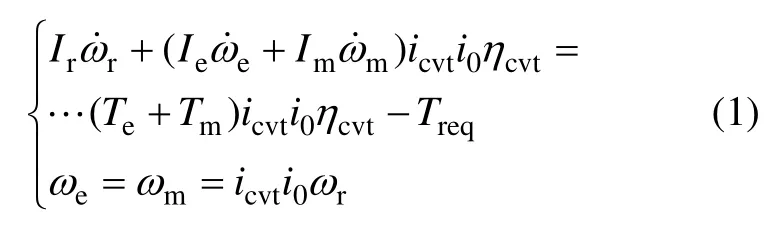
式中：Ir，Im和Ie分別為折算到車輪處、電機和發動機的轉動慣量，kg·m2； ω˙r， ω˙m和 ω˙e分別為車輪、電機和發動機的角加速度，rad/s2；icvt為CVT 速比；i0為減速器速比；ηcvt為傳動系效率；Tm為電機轉矩，N·m；Te為發動機轉矩，N·m；Treq為需求轉矩，N·m；ωr，ωm和ωe分別為車輪、電機和發動機的轉速，r/min。

1.3 關鍵動力部件模型

1) 發動機和ISG 電機模型。通過試驗，利用3次樣條插值擬合，得到發動機的油耗及電機效率數值模型，如圖2 和3 所示。

2) 電池數學模型。電池SOC 在充放電過程中的變化為

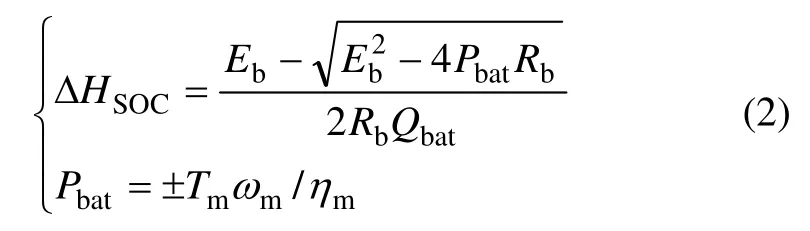
式中：ΔHSOC為電池SOC 的變化值；Eb為電池電動勢，V；Rb為電池的電阻，?；Qbat為電池組的容量，A·h；Pbat為電池消耗的功率，kW，放電過程中取正號，充電過程中取負號；ηm為電機的充放電效率。

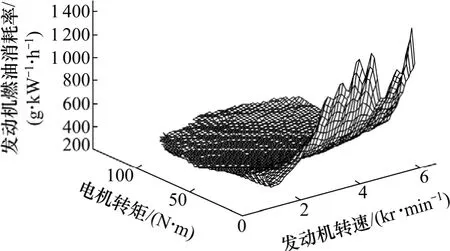
圖2 發動機油耗數值模型Fig.2 Numerical model of engine fuel consumption

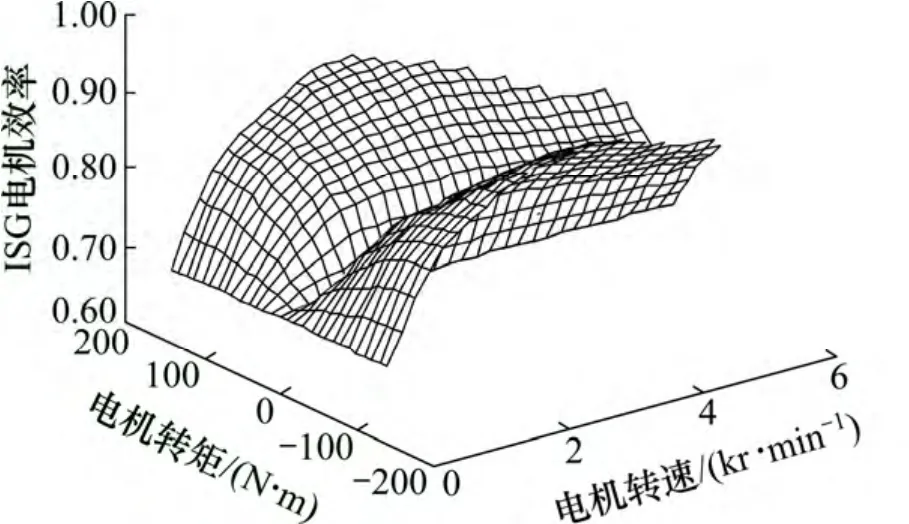
圖3 ISG 電機效率數值模型Fig.3 Numerical model of ISG efficiency

2 優化算法

針對動態規劃增加狀態變量會指數式增加計算時間的問題，本文優化算法的思路是將瞬時尋優與動態規劃全局尋優相結合，采用瞬時優化算法對CVT 的速比進行實時優化，進而將該實時優化結果嵌套在動態規劃算法中對循環工況進行全局尋優。

2.1 瞬時優化算法

CVT 車輛具有速比連續可變的特點，車輛在每個工作狀態(SOC、車速、加速度、坡度)下必然存在一個最佳的目標速比可使能耗經濟性最優。

PHEV 與普通意義上的混合動力汽車不同，其一部分能量來源于燃油，另一部分能量來源于電網充電，為了將這2 種能量統一起來，本文中目標函數QC定義為2 種能量消耗之和：

式中：tf為工況的終端時刻；αfuel和αelec為燃油與電消耗轉化為MJ 單位的轉化系數；Qfuel(t)為t 時刻消耗的燃油量，L/s；ηgrid為電網的充電效率，取0.98；Pbat(t)為t 時刻電池的充放電功率，放電時大于0 kW，充電時小于0 kW；β 為能量價格比，是一個可變參數，隨著市場上油價和電價的波動而波動，可表示為

式中：Selec和Sfuel分別為每消耗1 MJ 能量的電價和汽油的價格。

其中設計變量為icvt，約束條件為

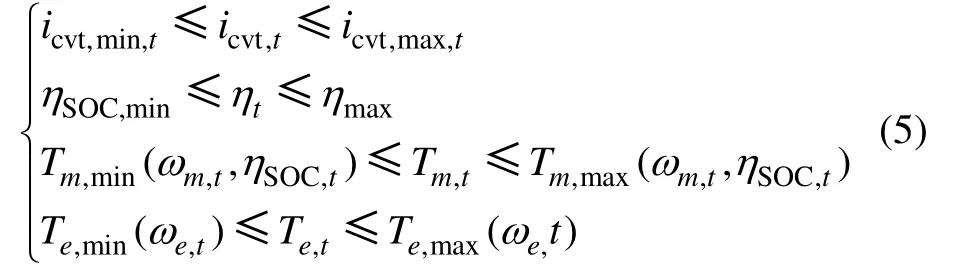
式中：ηSOC,t，ηSOC,min和ηSOC,max分別為電池荷電狀態時刻、最小值與最大值。

瞬時優化算法計算流程如圖4 所示。

2.2 動態規劃算法

動態規劃作為一種多階段決策問題的優化方法，可按時間或空間把問題分為若干個相互聯系的階段。具體到 PHEV 能量管理策略的優化問題上，應將選取的循環駕駛工況進行合理的離散化，這樣整個循環工況的整車能耗最優控制問題就轉換成為不同時間階段的決策問題。

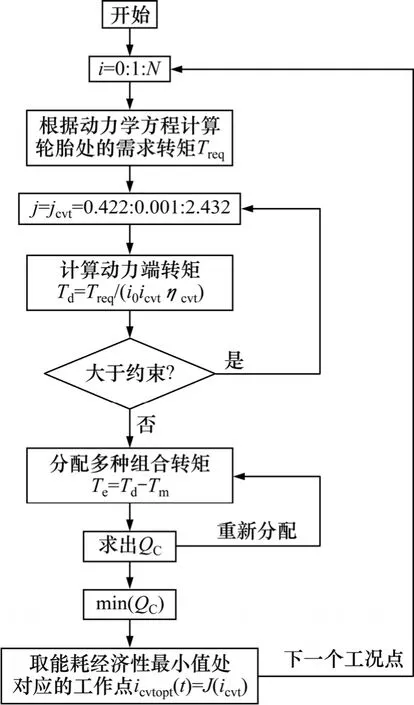
圖4 瞬時優化計算流程Fig.4 Instantaneous optimization process

通過以上分析，將循環工況離散為k 個階段，優化函數為

式中：x 為狀態變量；u 為控制變量；L 函數為k 階段的能耗經濟性，即

式中：σ 為懲罰因子；P (ηSOC(k))為懲罰函數，具體表示為

定義動力系統的狀態變量為

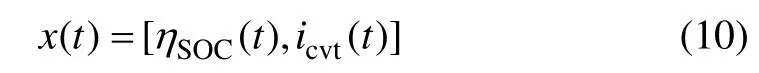
ηSOC轉移函數為

CVT 速比的轉移參考2.1 節。

控制變量為

狀態變量與控制變量的約束條件參考式(5)。

動態規劃的基本示意圖如圖5 所示。

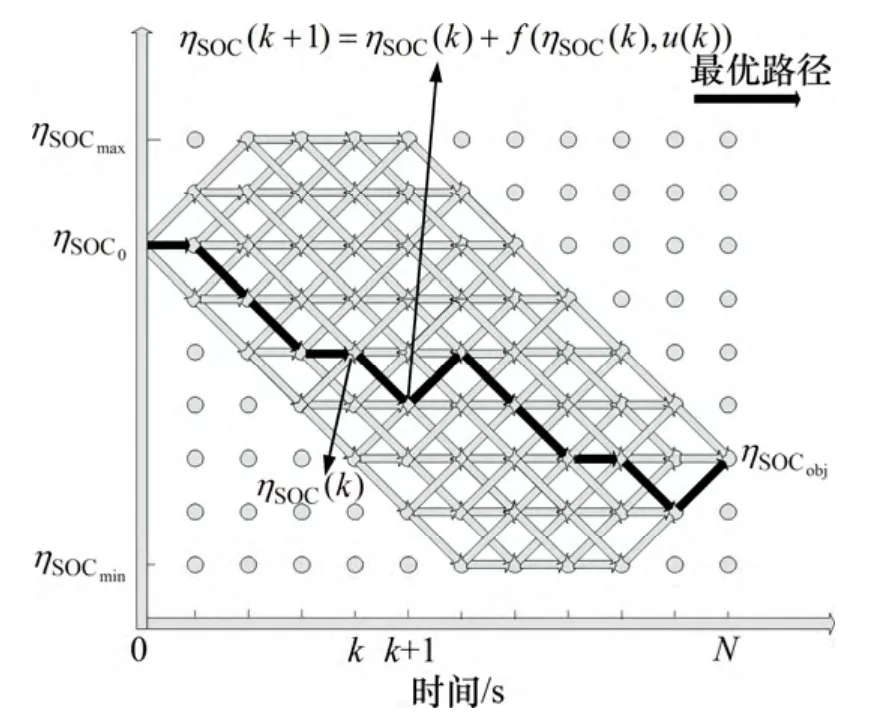
圖5 動態規劃求解示意圖Fig.5 Schematic diagram of dynamic programming solving

3 優化結果及分析

國內常采用城市+城郊循環工況(New European Driving Cycle, NEDC)對車輛經濟性進行評價，因此本文選取NEDC 作為車輛的循環工況，如圖6 所示。

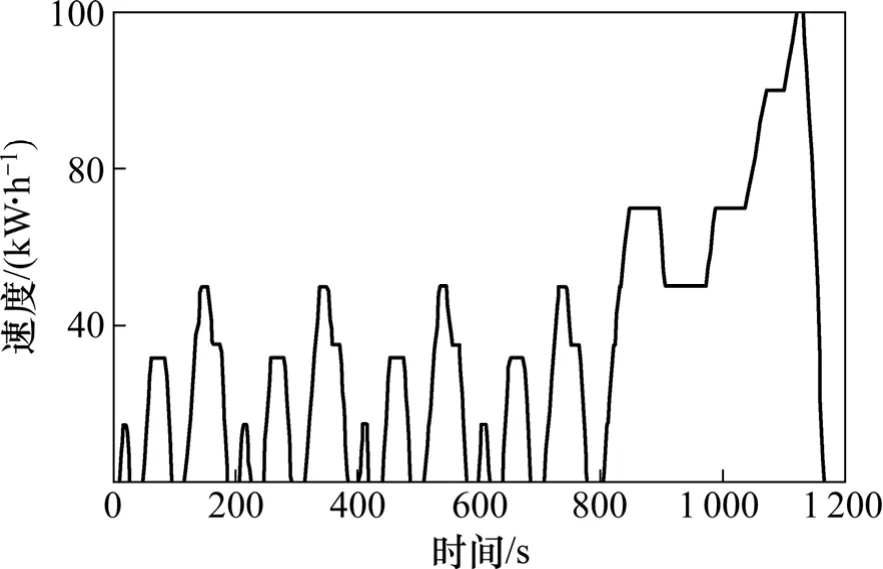
圖6 NEDC 循環工況Fig.6 NEDC driving condition

3.1 控制變量的優化結果及分析

為了更清楚地了解PHEV 動力源的功率分配，將NEDC 循環工況重復10 次，經過優化算法計算，得到了發動機功率與電機功率的分布。圖7 給出了第1 個和第10 個NEDC 工況的計算結果。可以看出，在第1個NEDC 工況下，主要以電機作為主要動力輸出源(通常所說的CD 模式)，在第10 個工況下，以電機和發動機共同作為動力輸出源(通常所說的CS 模式)。

圖7 發動機與電機功率的分布Fig.7 Power distribution of engine and motor

為了更清晰地了解電機和發動機的動力分配，圖8 與9 分別給出了電機和發動機在不同模式下的工作點，可以看出：在CD 模式下，電機工作的頻率較高，基本都處于高效區，發動機只有少量工作點，發動機參與工作的原因為此時的轉矩需求較大，超過了電機所能提供的最大轉矩；在CS 模式下，電機的工作點相對連貫(有些工作點對應于電機單獨驅動，有些工作點對應于混合驅動)，發動機的工作點較多且基本沿發動機的最佳經濟性曲線工作，說明采用CVT 和優化算法能對電機和發動機進行合理的控制，從而獲得較好的能耗經濟性。

圖8 電機的工作點Fig.8 Working point of motor

3.2 狀態變量的計算結果及分析

經過路徑優化，得到了CVT 速比和電池SOC 在不同工況點下的具體數值，如圖10～11 所示。從圖10可以看出：CVT 的狀態點基本處于高效率區域，只是在CD 與CS 模式下的工作點不同,原因是在CS 模式下發動機參與工作的次數增加。

圖9 發動機的工作點Fig.9 Working point of engine

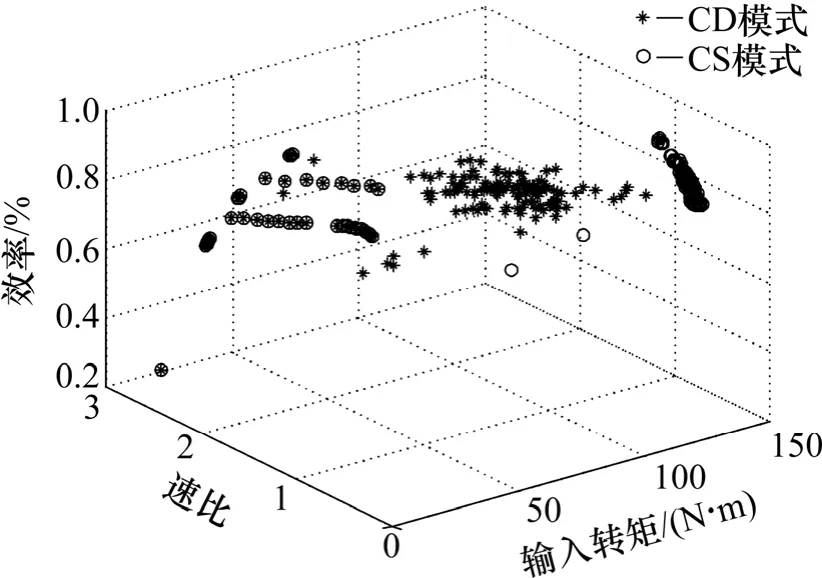
圖10 CVT 的狀態點Fig.10 State point of CVT

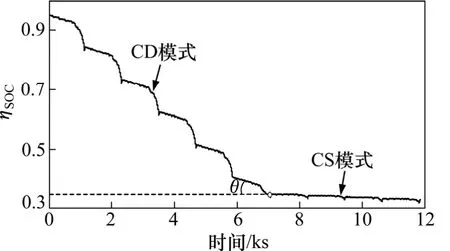
圖11 電池SOC 的狀態變化曲線Fig.11 State curve of battery SOC

圖11 所示為電池SOC 的狀態轉移軌跡，它按照CDCS 工作模式的特性變化；為了更直觀地了解電池SOC 在CD 模式的消耗速度，引入圖11 中所示的θ角來作為CD 模式與CS 模式的切換時刻，本次計算中為40.9°。

4 控制策略的數值擬合

上述優化算法存在計算量過大的問題，不能應用到實車上作為車輛的在線能量管理策略，但可以依據計算結果，對電機和發動機的工作點進行提取，從而制定出既符合 PHEV 特點又滿足車輛能量管理實時性要求的在線能量管理策略。

4.1 基于BP 神經網絡的控制策略

采用BP 神經網絡分別對PHEV 的CD 和CS 工作模式進行擬合，利用函數newff 創建網絡，設定網絡輸入層為車速和需求扭矩，輸出層為電機和發動機的轉矩，生成含有一個隱層的BP 網絡，神經元個數為30，定義隱含層傳遞函數為tansig，輸出層傳遞函數為purelin，訓練函數為train。

將10 個NEDC 工況(11 850 個工作點)仿真結果中的11 450 個工作點作為訓練點，400 個工作點作為驗證擬合精度的高低，如圖12～15 所示。由圖12～15 可以看出：擬合輸出與期望輸出比較接近，在可接受范圍之內。

圖12 CD 模式下電機工作點的擬合精度Fig.12 Fitting accuracy of motor operating point in CD mode

圖13 CD 模式下發動機工作點的擬合精度Fig.13 Fitting accuracy of engine operating point in CD mode

圖14 CS 模式下電機工作點的擬合精度Fig.14 Fitting accuracy of motor operating point in CS mode

圖15 CS 模式下發動機工作點的擬合精度Fig.15 Fitting accuracy of engine operating point in CS mode

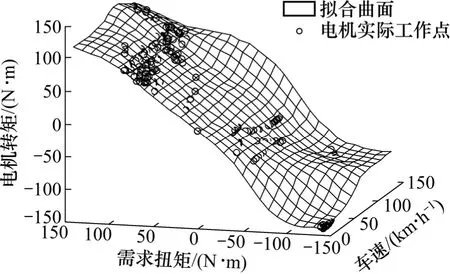
圖16 CD 模式下電機的工作曲面Fig.16 Working surfaces of motor in CD mode

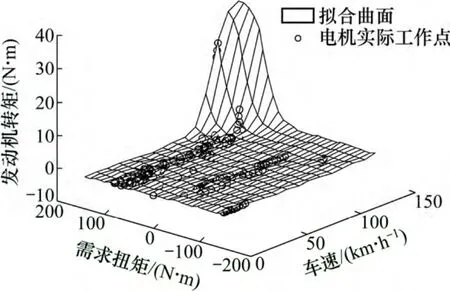
圖17 CD 模式下發動機的工作曲面Fig.17 Working surfaces of engine in CD mode

圖18 CS 模式下電機的工作曲面Fig.18 Working surfaces of motor in CS mode

經過BP 擬合得到電機與發動機的優化控制MAP圖，如圖16～19 所示。根據行駛工況相應的驅動需求轉矩和車速直接查表獲得電機和發動機的扭矩輸出量，從而實現控制策略的優化，其結果可用于車輛的實時控制。

4.2 BP 控制策略的仿真結果

根據matlab/simulink 仿真平臺搭建仿真模型，分別對門限值控制策略[10-12]和BP 控制策略進行了仿真計算，仿真結果如表1 所示。由表1 可以看出：在NEDC、城市測功器駕駛進程(UDDS)和高速路燃油經濟測試(HWFET)循環工況下，BP 控制策略比DP 算法的能耗經濟性要差，但與門限值控制策略相比能耗經濟性分別有10.09%，9.89%和8.17%的提高。

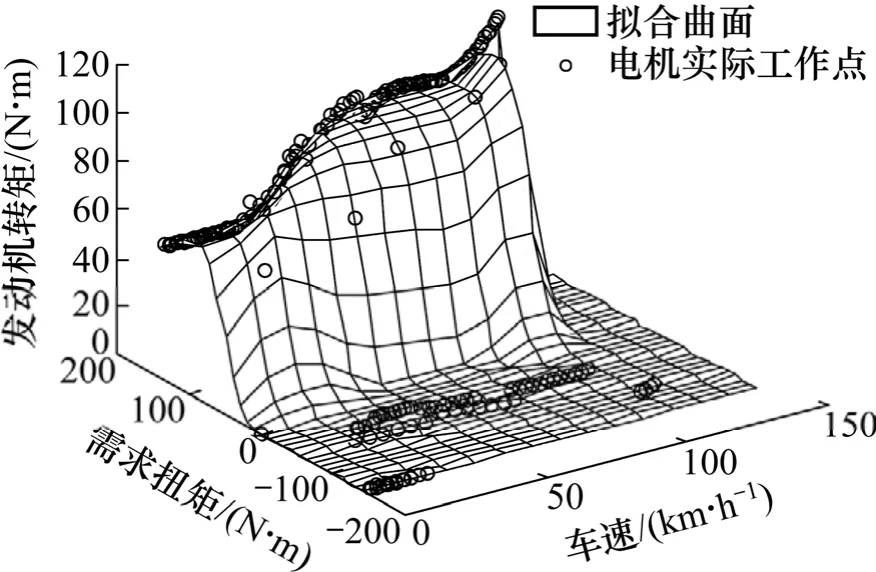
圖19 CS 模式下發動機的工作曲面Fig.19 Working surfaces of engine in CS mode

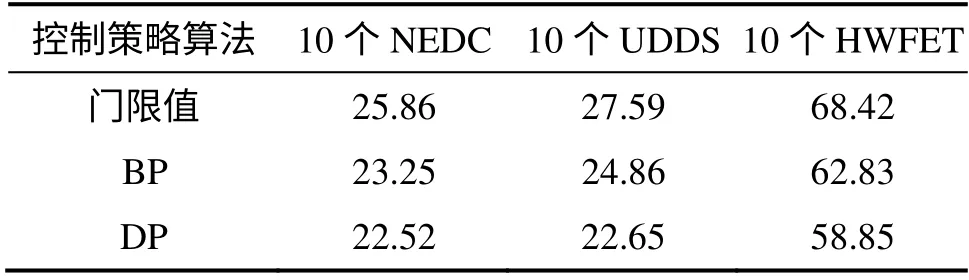
表1 不同工況的能耗經濟性Table 1 Energy consumption economy of different conditions 元

5 結論

1) 針對新型單電機PHEV，采用瞬時優化算法對CVT 的速比進行實時優化，進而將該實時尋優結果嵌套在動態規劃算法中，以CVT 速比和電池SOC 為狀態變量，電機和發動機功率為控制變量，對循環工況進行全局尋優，得到電機和發動機間的功率分配。

2) 采用BP 神經網絡對發動機與電機的工作點進行訓練擬合，得到電機與發動機的優化控制MAP 圖，用于車輛在循環工況的實時控制。

3) 在matlab/simulink 的仿真平臺上搭建模型進行仿真計算，結果表明BP 控制策略與門限值控制策略相比，可使采用CVT 的PHEV 的能耗經濟性在NEDC，UDDS 和HWFET 循環工況下分別有10.09%，9.89%和8.17%的提高。

[1] GENG Bo, James K, SUN Dong. Energy management control of micro turbine-powered plug-In hybrid electric vehicles using the telemetry equivalent consumption minimization strategy[J].IEEE Transactions on Vehicular Technology, 2011, 60(9):4238-4248.

[2] CHEN Zhang, Ardalan V. Route preview in energy management of plug-in hybrid vehicles[J]. IEEE Transactions on Control Systems Technology, 2012, 20(2): 546-553.

[3] YANG Bin, LI Yaoyu, GONG Qiuming, et al. Multi-information integrated trip specific optimal power management for plug-In hybrid electric vehicle[C]//American Control Conference. St Louis: ACC, 2009: 4607-4612.

[4] GONG Qiuming, LI Yaoyu, PENG Zhongren. Trip-based optimal power management of plug-In hybrid electric vehicle[J].IEEE Transactions on Vehicular Technology, 2008, 57(6):3393-3401.

[5] 張博, 鄭賀悅, 王成. 可外接充電混合動力汽車能量管理策略[J]. 機械工程學報, 2011, 47(6): 113-119.ZHANG Bo, ZHENG Heyue, WANG Cheng. Plug-in hybrid electric vehicle energy management strategy [J]. Journal of Mechanical Engineering, 2011. 47(6): 113-119.

[6] Moura S J, Duncan S, et al. Tradeoffs between battery energy capacity and stochastic optimal power management in plug-in hybrid electric vehicles[J]. Journal of Power Sources, 2010, 195:2979-2988.

[7] Scott M, Hosam K, Duncan S, et al. A stochastic optimal control approach for power management in plug-In hybrid electric vehicles[J]. IEEE Transaction on Control Systems Technology,2011, 19(3): 545-555.

[8] Mojtaba S Z, Abbas Z K, Steffen K, et al. Integrated thermal and energy management of plug-in hybrid electric vehicles[J].Journal of Power Sources, 2012, 216: 237-248.

[9] 舒紅, 聶天雄, 鄧麗君, 等. 插電式混合動力汽車模型預測控制[J]. 重慶大學學報, 2011, 34(5): 36-41.SHU Hong, NIE Tianxiong, DENG Lijun, et al. Model predictive control for a plug-in hybrid electric vehicle[J]. Journal of Chongqing University, 2011, 34(5): 36-41.

[10] Banvait H, Anwar S, CHEN Yaobin. A rule-based energy management strategy for plug_in hybrid electric vehicle(PHEV)[C]//American Control Conference. St Louis: ACC, 2009:3938-3943.

[11] Fajri P, Asaei B. Plug-in hybrid conversion of a series hybrid electric vehicle and simulation comparison[C]//International Conference on Optimization of Electrical and Electronic Equipment. Brasov: OPTIM, 2008: 287-292.

[12] ZHANG Song, WU Guangqiang, ZHENG Songlin. Study on the energy management strategy of DCT-based series-parallel PHEV[C]//International Conference on Computing Control and Industrial Engineering. Wuhan: CCIE, 2010: 25-29.