超超臨界機組高壓內缸蠕變強度分析

喻 超， 王煒哲， 張軍輝， 劉應征

（1.上海交通大學 機械與動力工程學院，動力機械與工程教育部重點實驗室，上海 200240；2.上海交通大學 燃氣輪機研究院，上海 200240；3.上海電氣電站設備有限公司上海汽輪機廠，上海 200240）

隨著超超臨界機組汽輪機技術的發展，汽輪機 的進汽參數不斷提高，高溫構件蠕變失效問題日益受到重視.其中，高壓內缸是超超臨界機組的關鍵部件之一，因長期承受高溫、高壓蒸汽，從而導致高壓內缸結構發生高溫蠕變力學行為，進一步降低高壓內缸的蠕變斷裂韌性.因此，保證高壓內缸在服役期內長時間安全運行，考核高壓內缸高溫蠕變強度是設計超超臨界機組高壓內缸必須考慮的重要問題.

近年來，國內外相關學者對汽輪機內缸進行了許多研究.Hakl等［1］對帶有裂紋缺陷的內缸進行了剩余壽命分析；Choi等［2］利用有限元方法，使用非彈性分析對高壓內缸進行了壽命評估；胡怡豐等［3］對超超臨界中壓內缸的高溫蠕變強度進行了研究；金永明等［4］使用二維有限元模型對超超臨界機組高壓內缸進行了有限元強度分析.由以上文獻可以看出，研究主要集中在內缸的壽命分析方面，而針對超超臨界機組高壓內缸高溫蠕變強度分析以及考核的研究較少.

筆者以某百萬千瓦超超臨界火電機組高壓內缸為研究對象，采用有限元方法建立高壓內缸三維有限元分析模型，使用蠕變冪律模型和多軸應力下的孔洞長大機理對高壓內缸在長時間工作下的蠕變行為進行分析，得到了蠕變發生的典型區域及蠕變應變值，并重點分析了高壓內缸的應力、應變分布及其考核方法以及2×105h蠕變后高壓內缸中分面的密封性能.

1 高壓內缸計算模型

高壓內缸工作在高溫、高壓的蒸汽環境中，承受蒸汽壓力的同時還與蒸汽進行強烈的熱交換，由于各部位溫度分布不均勻，變形不協調，從而在結構內部產生熱應力，并在高溫環境下產生蠕變.筆者采用ABAQUS有限元軟件，通過熱力耦合分析方法獲得高壓內缸的溫度場、應力場以及運行2×105h后的蠕變應變場，進而分析討論高壓內缸高溫蠕變強度以及考慮螺栓松弛效應后中分面的密封性能.

1.1 熱力耦合有限元模型

高壓內缸溫度場計算中，假設內缸材料各向同性，無內熱源.根據傅里葉定律及能量守恒定理，其三維瞬態熱傳導方程為［5］

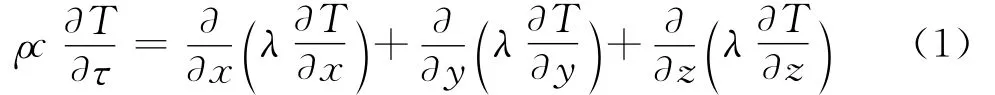
式中：ρ為微元體密度，kg/m3；c為微元體比熱容，J/（kg·K）；T 為溫度，K；τ為時間，s；λ為導熱系數，W/（m·K）.

恒壁溫、恒熱流及給定對流的第三類邊界條件如式（2）所示.

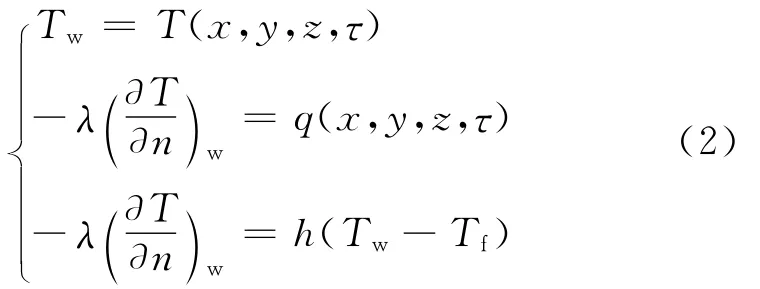
式中：T（x，y，z，τ）為邊界溫度函數；q（x，y，z，τ）為邊界上熱流密度函數；n為壁面法線方向；h為表面對流傳熱系數，W/（m2·K）；Tw和Tf分別為邊界壁面溫度和近壁面流體溫度，K.

根據伽遼金法［6］建立n節點溫度的矩陣方程，得到溫度場的有限元格式為

式中：C為比熱容矩陣；K為導熱系數矩陣；P為溫度載荷矩陣；T為節點溫度矩陣；T·為節點溫度對時間的導數矩陣.

最后形成的熱力耦合分析矩陣方程如下［7］

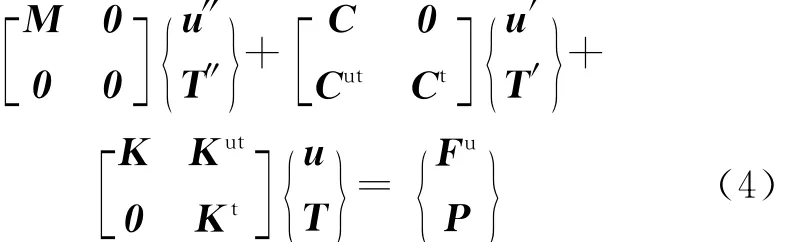
式中：u為節點位移向量；u′為節點位移對時間的導數向量；u″為節點位移對時間的二階導數向量；T′為節點溫度對時間的導數向量；T″為節點溫度對時間的二階導數向量；M為單元質量矩陣；Ctu為單元熱彈性阻尼矩陣；Kut為單元熱彈性剛度矩陣；Ct為單元比熱容矩陣；Kt為單元擴散導熱矩陣；Fu為單元節點力向量.

1.2 高壓內缸有限元離散模型

由于高壓內缸采用單向通流且上、下結構對稱，將高壓內缸下半缸作為計算分析模型，如圖1所示.計算單元類型采用四節點、四面體、三維線性積分熱力耦合單元C3D4T，計算域單元總數為589 696，節點數為120 308，如圖2所示.

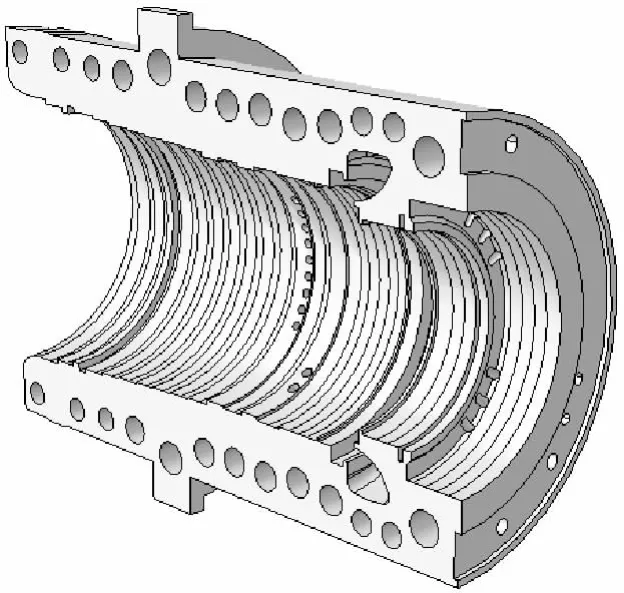
圖1 高壓內缸的幾何模型Fig.1 Geometry model of the high－pressure inner casing

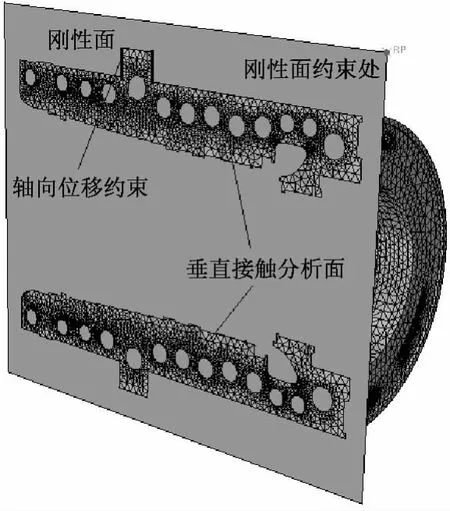
圖2 高壓內缸網格劃分Fig.2 Meshing of the high－pressure inner casing

1.3 邊界條件

高壓內缸材料為某改良9Cr鋼，由于汽缸內部溫度較高且變化較大，計算中充分考慮材料的非線性特征.

熱邊界條件：高壓內缸與蒸汽的換熱采用第三類邊界條件，高壓內缸不同溫度區域施加不同的表面傳熱系數和流體溫度，主流蒸汽的溫度和壓力取自汽輪機熱力設計.由于缺乏超超臨界機組高壓內缸各部位表面傳熱系數的實測數據，筆者采用文獻［8］所推薦的經驗關系式，傳熱系數計算分為進汽口、排汽口、抽汽腔、光滑內表面、動葉頂部汽封、靜葉根槽、平衡孔及冷卻孔等部位.

力邊界條件：高壓內缸所承受的載荷包括蒸汽壓力載荷和螺栓預緊力載荷，在高壓內缸不同區域施加相應的蒸汽壓力，因垂直截面處（即螺栓密封面處）的平面對稱性，采用一剛性面與其進行接觸分析，可達到1/2結構相同的計算效果，計算效率得到極大提高，如圖2所示.

1.4 螺栓熱緊力及其松弛

螺栓與高溫部件線膨脹系數的不同以及溫度分布的不均導致螺栓熱態預緊力（以下簡稱熱緊力）隨工作狀態的變化而變化，且不同于螺栓冷態安裝時的預緊力.螺栓熱緊力受到螺栓材料和法蘭材料的彈性模量、線膨脹系數、溫差及相對面積的影響，通過計算可得到高壓內缸不同位置螺栓在穩態運行時的熱緊力.同時，由于螺栓在高溫環境下長時間工作，將產生松弛，從而使得密封緊力不斷減小，影響高壓內缸的密封性能.文獻［9］給出的基于時間硬化的螺栓松弛模型可以較好地與實驗結果吻合，如式（5）所示.

式中：σ為物體承受的應力，MPa；σ0為螺栓熱緊力，MPa；E為螺栓材料的彈性模量，MPa；B、m和n為材料蠕變參數；t為蠕變時間，h.

不同溫度下材料蠕變參數不同，如500℃下，B＝5.059 47×10－16、m＝0.422 87、n＝4.862 12.

1.5 高壓內缸蠕變強度分析方法

高壓內缸的蠕變行為受長期工作狀態（溫度及包括熱應力在內的內部應力）所影響，因此對高壓內缸進行穩態熱彈塑性耦合分析，以獲得穩態工況下高壓內缸的溫度場以及應力應變場分布.蠕變是一種在持久應力作用下與時間有關的塑性變形，一般可分為硬化、穩態和損傷3個階段.筆者采用陳化理論的冪率模型來計算蠕變應變速率［10］，其表達式如下

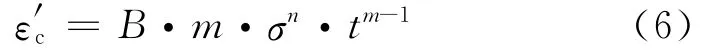
式中：ε′c為蠕變應變速率.

材料蠕變試驗參數大多在單軸條件下獲得，而高壓內缸工作在復雜的多軸應力狀態下，由于電廠高溫部件的失效機理大多是受約束孔洞長大機理，相關設計標準中主要引入基于受約束孔洞長大機理的 Cocks－Ashby模型.式（7）給出了 Cocks－Ashby模型的多軸應力與單軸應力蠕變失效應變關聯式［3］

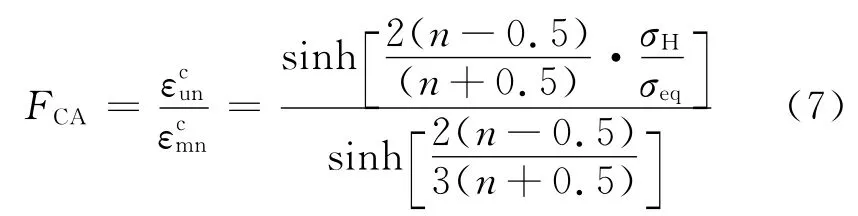
式中：FCA為 Cocks－Ashby系數、分別為單軸蠕變應變和多軸等效應變；σH、σeq分別為靜水應力和Mises等效應力，MPa.

2 高壓內缸蠕變強度

2.1 高壓內缸穩態溫度場

圖3給出了高壓內缸穩態運行時的溫度場分布.通常合金鋼工作溫度高于420℃時必須考慮蠕變問題.由圖3可知，高壓內缸大部分區域工作溫度均超過蠕變溫度，必須對其蠕變強度進行考核.

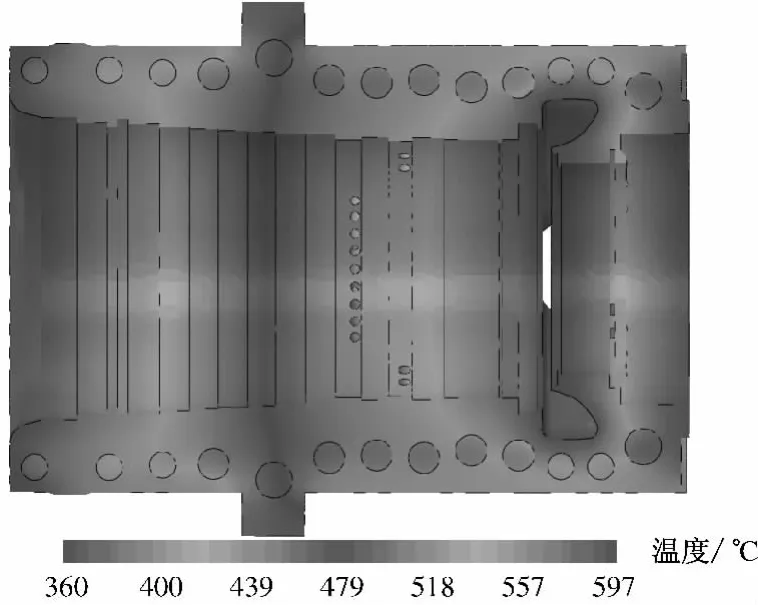
圖3 高壓內缸穩態溫度場Fig.3 Steady－state temperature field of the HP inner casing

2.2 高壓內缸穩態應力場及蠕變應力場

圖4給出了穩態運行工況下高壓內缸的Mises應力分布.由圖4可知，最大Mises應力分布于螺栓沉孔下表面，為424 MPa，主要原因是此處施加了螺栓預緊力，根據彈性力學圣維南原理［11］可知，螺栓載荷只在局部產生效應而對內缸遠處其他部位沒有影響.由圖4還可知，高壓內缸其他部位最大應力為200 MPa左右，分布于高壓內缸進汽口以及平衡活塞端部位置，低于此處溫度597℃所對應的材料屈服強度451 MPa，未達到屈服狀態.

圖4 穩態工況下高壓內缸的Mises應力分布Fig.4 Steady－state Mises stress field of the HP inner casing

高壓內缸不同位置螺栓在穩態運行時的熱緊力不同，由于螺栓在高溫環境下長時間工作將產生蠕變松弛，進而產生熱緊力的變化.圖5給出了1號螺栓（高壓內缸進汽口到排汽口方向排列1號～13號螺栓）經歷2×105h蠕變過程中熱緊力隨時間的變化.由圖5可見，熱緊力存在明顯的松弛過程，在蠕變最初階段，熱緊力急劇減小，當熱緊力變化到某一值之后，蠕變變形對熱緊力的影響越來越微弱，此時熱緊力呈緩慢變化狀態.同理其余螺栓也有類似變化過程.

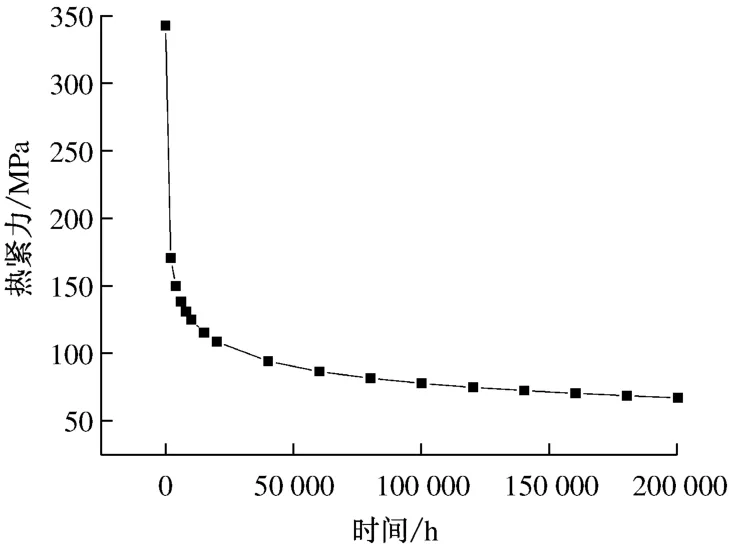
圖5 熱緊力隨時間的變化曲線Fig.5 Bolt tightening force vs.time

圖6給出了高壓內缸經歷2×105h蠕變后蠕變應力的分布云圖.由圖6可知，最大蠕變應力同樣分布于螺栓沉孔下表面，為309 MPa，低于穩態運行時的峰值應力.這是由于發生蠕變塑性應變時，釋放了部分內應力，高壓內缸應力場發生了重新分配.對比圖4和圖6可知，2×105h蠕變后，高壓內缸進汽口及平衡活塞位置的平均應力狀態從高應力（144 MPa）下降到低應力（33 MPa），由此可以說明，高壓內缸進汽口及平衡活塞處為蠕變應變變化的典型區域.

圖6 2×105 h蠕變后高壓內缸的蠕變應力分布Fig.6 Creep stress field of the HP inner casing after 2×105 h

圖7給出了中分面進汽口處A點的Mises應力隨時間的變化曲線.由圖7可見，高壓內缸應力存在明顯的松弛過程，在蠕變最初階段，應力有一個急劇減小的過程，當應力變化到某一值之后，蠕變變形對應力的影響越來越弱，此時應力呈緩慢變化狀態.而蠕變速率受應力控制，因此當應力值趨于恒定時，蠕變應變將保持緩慢增長狀態.

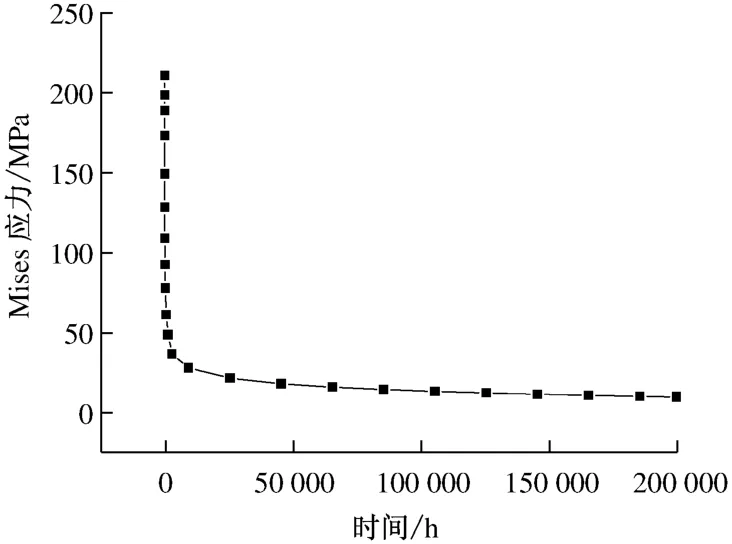
圖7 高壓內缸A點Mises應力隨時間的變化曲線Fig.7 Mises stress at point A in HP inner casing vs.time

2.3 多軸蠕變等效應變

除對高壓內缸進行應力控制外，對其應變進行控制也是必不可少的［12］.目前，工程上運用較多的應變控制準則為ASME標準，其中規定：（1）截面平均應變小于1%；（2）平均應變加彎曲應變小于2%；（3）峰值應變小于5%.實際上，蠕變斷裂數據大多來自單軸試驗結果，而上述應變準則并沒有考慮多軸應力狀態的影響，應變控制同樣需要根據三向應力狀態來進行設定.圖8給出了基于Mises應力的高壓內缸2×105h蠕變后的單軸蠕變等效應變分布.由圖8可以看出，蠕變等效應變主要發生在進汽口及平衡活塞位置，這也進一步說明了該位置發生的應力松弛現象（見圖4和圖6）.單軸最大蠕變等效應變為0.005 56，遠遠低于考核規范許用值，為進一步驗證蠕變強度，筆者采用式（7）進行多軸等效蠕變特性計算分析，結果見圖9.

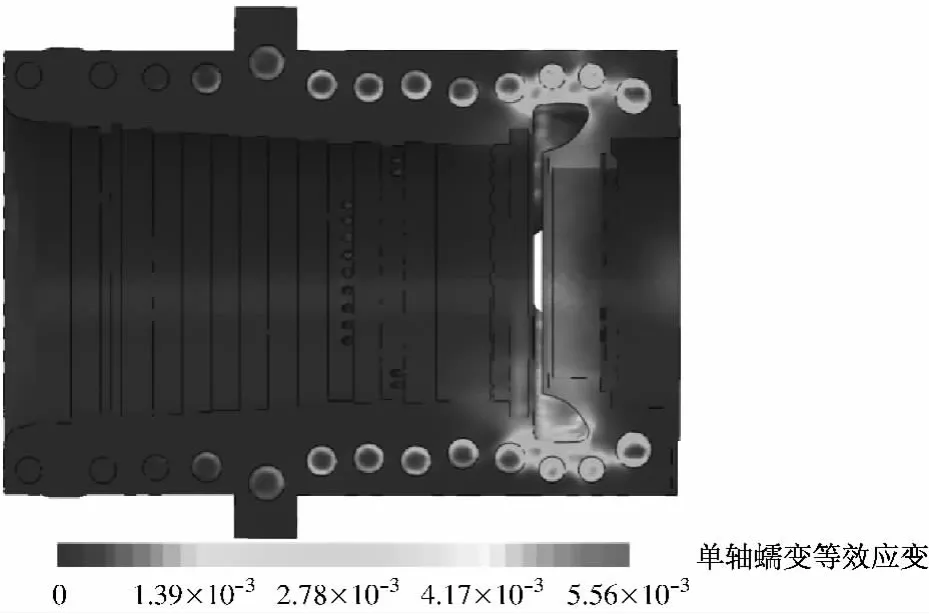
圖8 高壓內缸單軸蠕變等效應變Fig.8 Equivalent uniaxial strain of the HP inner casing

圖9 高壓內缸多軸蠕變等效應變Fig.9 Equivalent multiaxial strain of the HP inner casing

由圖9可知，2×105h蠕變后，最大多軸蠕變等效應變發生在右數第二級螺栓沉孔下表面，為0.058 83（主要原因是此處施加了螺栓預緊力載荷，造成局部變形過大，不是真實應變值）.以圖4中特征點A作為參考，A點的單軸蠕變等效應變值為0.001 84，而多軸蠕變等效應變值為0.016 9，約為單軸時的9.2倍，危險性遠遠大于單軸時的蠕變等效應變值.同時，由圖9可知，除螺栓沉孔位置外，高壓內缸其他區域的多軸蠕變等效應變峰值均低于5%，截面平均蠕變等效應變亦低于1%，滿足應變考核準則.對比圖8和圖9可知，因多軸蠕變危險性大于單軸蠕變，因此進行蠕變強度考核時采用多軸蠕變等效應變值更安全.

3 高壓內缸中分面汽密性分析

汽缸中分面的密封性能有以下影響因素：（1）螺栓熱緊力隨工作狀態的變化而變化；（2）螺栓在高溫環境下的蠕變松弛將使密封緊力不斷減小；（3）汽缸的蠕變將使密封面應力重新分配.因此，為準確考核中分面的汽密性，筆者采用式（5）對螺栓進行應力松弛分析，并充分考慮螺栓的松弛及線脹差的影響，同時對中分面采用接觸邊界來模擬密封效果.

圖10和圖11分別給出了高壓內缸2×105h蠕變前后中分面接觸應力的分布情況.由圖10和圖11可以看出，在高壓內缸內側的Ⅰ、Ⅳ區域及外側的Ⅱ、Ⅲ區域（同理汽缸下半區域）存在接觸應力接近0的現象，但其他區域接觸良好，可以有效防止內側腔室的蒸汽泄漏.對比兩圖可以看出，接觸面上的接觸應力由最大值403 MPa減小為147 MPa，應力最大區域也由蠕變前進汽口位置變為平衡活塞部位，應力發生了重新分配，從而更進一步說明了高壓內缸蠕變變形對接觸應力即密封性能的影響.

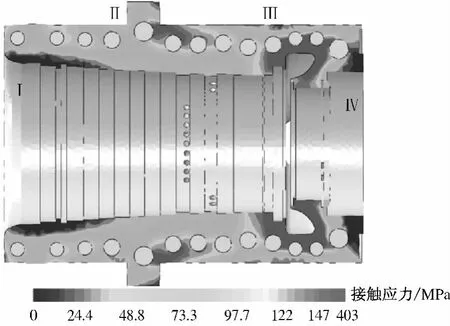
圖10 高壓內缸穩態工況下中分面接觸應力分布Fig.10 Distribution of steady－state contact stress on the HP inner casing split

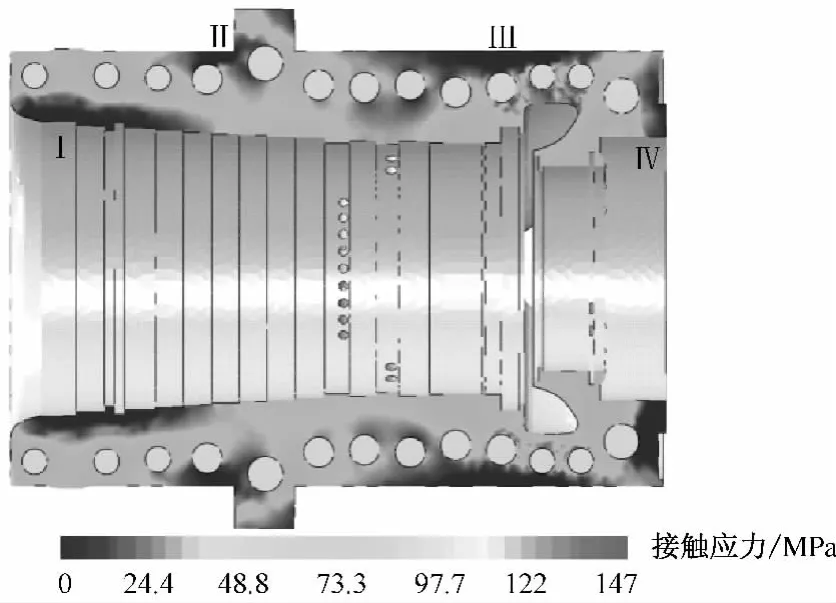
圖11 2×105 h蠕變后高壓內缸中分面接觸應力分布Fig.11 Contact stress distribution on the HP inner casing split after 2×105 h

圖12和圖13分別給出了2×105h蠕變前后中分面接觸區域的張開位移分布云圖，定量給出了Ⅰ、Ⅱ、Ⅲ和Ⅳ區域的張開位移數據，直觀反映了汽缸的密封性能.

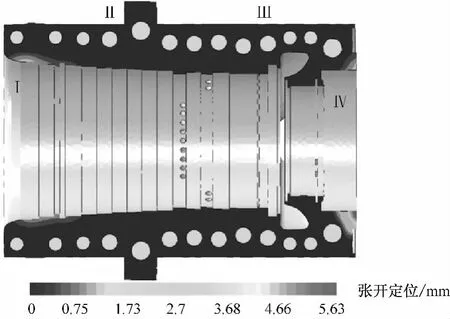
圖12 高壓內缸穩態工況下中分面張開位移分布Fig.12 Distribution of steady－state opening displacement on the HP inner casing split

圖13 2×105 h蠕變后高壓內缸中分面張開位移分布Fig.13 Opening displacement distribution on the HP inner casing split after 2×105 h

4 結 論

（1）在穩態工況下，高壓內缸最大應力低于相應溫度下材料的屈服強度，高壓內缸溫度分布在360～600℃，已進入蠕變溫度范圍，因此進行蠕變強度考核是有必要的.

（2）高壓內缸蠕變應變發生區域主要集中在進汽口及平衡活塞處.蠕變應變釋放了高壓內缸部分內應力，其應力場發生了重新分配，蠕變應力峰值低于穩態工況下高壓內缸的應力峰值，進汽口及平衡活塞處發生明顯應力松弛現象.

（3）多軸應力對蠕變考核具有重要影響，基于孔洞長大理論的Cocks－Ashby模型計算結果表明，在多軸應力下蠕變等效應變發生顯著變化，危險性將增加.應當采用多軸蠕變等效應變來進行蠕變強度的考核.

（4）高壓內缸蠕變變形對密封性能具有重要影響.由于蠕變所引起的應力松弛使得螺栓熱緊力減小以及高壓內缸蠕變變形，2×105h蠕變后，高壓內缸中分面部分區域存在接觸應力接近0的現象，這部分接觸間隙較小，但仍能保證高壓內缸的汽密性，對高壓內缸中分面的螺栓位置分布具有重要的指導意義.

［1］ HAKL J，BIELAK O，VLASAK T.Residual life assessment of steam turbine casing containing crack defect［J］.International Journal of Pressure Vessels and Piping，2001，78（11/12）：977－984.

［2］ CHOI Woosung，HYUN Jungseob.A life assessment for steam turbine casing using inelastic analysis［J］.Modern Physics Letters B，2008，22（11）：1141－1146.

［3］ 胡怡豐，黃慶華，康明.超超臨界機組再熱溫度提升對中壓內缸設計影響的研究［C］//中國動力工程學會透平專業委員會2012年學術研討會論文集.江蘇：中國動力工程學會，2012：31－36.

［4］ 金永明，張媛.超超臨界參數汽輪機高壓內缸有限元強度分析［J］.熱力透平，2007，36（1）：11－14.JIN Yongming，ZHANG Yuan.HP inner cylinder FEM analysis for large ultra－supercritical steam turbine［J］.Thermal Turbine，2007，36（1）：11－14.

［5］ 楊世銘，陶文銓.傳熱學 ［M］.4版.北京：高等教育出版社，2009.

［6］ 王勖成.有限單元法［M］.北京：清華大學出版社，2011.

［7］ 謝永慧，鄧實，張荻，等.汽輪機轉子焊接的三維有限元數值模型研究［J］.熱力透平，2010，39（1）：12－18.XIE Yonghui，DENG Shi，ZHANG Di，et al.Study on numerical model for welding process of steam turbine rotor based on three－dimensional finite element method［J］.Thermal Turbine，2010，39（1）：12－18.

［8］ 史進淵，楊宇，鄧志成，等.超臨界和超超臨界汽輪機汽缸傳熱系數的研究［J］.動力工程，2006，26（1）：1－5.SHI Jinyuan，YANG Yu，DENG Zhicheng，et al.Casing＇s heat transfer coefficients of supercritical and ultra－supercritical steam turbines［J］.Journal of Power Engineering，2006，26（1）：1－5.

［9］ 郭進全，段非，苗曉鵬，等.基于時間硬化理論的應力松弛簡化歸一模型［J］.機械強度，2012，34（6）：930－933.GUO Jinquan，DUAN Fei，MIAO Xiaopeng，et al.Simplified and normalized model for stress relaxation based on time－harden rule［J］.Journal of Mechanical Strength，2012，34（6）：930－933.

［10］ 穆霞英.蠕變力學［M］.西安：西安交通大學，1990.

［11］ 徐芝綸.彈性力學［M］.北京：高等教育出版社，2006.

［12］ 史進淵，楊宇，鄧志成.大功率電站汽輪機壽命預測與可靠性設計［M］.北京：中國電力出版社，2011.