極化空時自適應處理性能分析

杜文韜,廖桂生,楊志偉

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

極化空時自適應處理性能分析

杜文韜,廖桂生,楊志偉

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

在建立極化空時信號模型的基礎上,對全維空時自適應處理(STAP)的輸出信雜噪比的計算式進行了分析,對比了該情況下極化空時自適應處理與STAP的性能,并指出了影響極化空時自適應處理性能的幾個主要因素.仿真結果驗證了分析結論的正確性.

極化雷達;目標檢測;極化信號處理;空時自適應處理

運動平臺雷達檢測地面目標具有檢測范圍廣、發現目標迅速等優點,正在成為地面動目標檢測的重要體制.但是,平臺運動將產生場景雜波的多普勒展寬,慢速目標常淹沒在雜波中難以檢測.針對這一問題,采用空時二維自適應處理[1-3]可有效利用空間角度和多普勒信息抑制雜波,提高系統的最小可檢測速度(MDV)[4].然而,由于運動平臺下雷達孔徑受到限制,最小可檢測速度常常不能滿足需要.

為了進一步提高系統對慢速目標的檢測能力,結合雷達回波的極化信息[5],進行極化、空間角度、多普勒三維自適應處理,可在不增加天線孔徑的前提下提高系統的MDV,相比于空時二維算法具有更好的慢速目標檢測性能.迄今為止,極化空時自適應算法的研究已經獲得了大量的成果.文獻[6]基于廣義似然比(GLR)原理提出了一種自適應極化空時目標探測算法(SPST-GLRT),接近最優處理效果;文獻[7]提出一種自適應極化空時聯合雷達目標探測算法(PST-GLR),該方法僅在角度域和多普勒域指定引導向量,而極化域沒有指定,從而降低了算法的實現復雜度;為解決算法所需要的訓練數據數量過大的問題,文獻[8]在極化空時域引入局域化處理方法;文獻[9]在HH和VV兩極化通道數據模型下對極化空時自適應算法進行了分析,但是缺少對全極化通道下的檢測性能分析;文獻[10]提出將極化空時自適應算法從接收一對同極化數據推廣至全極化數據,但并沒有深入地、理論地分析全維處理的性能.

在上述分析的基礎上,筆者首先推導了全極化通道數據下的完全極化波與非完全極化波的信號模型,定量地對比了極化空時自適應算法與空時二維算法的性能,并分析得到了如下結論:(1)增加極化信息可以改善空時自適應處理的檢測性能.(2)目標與雜波極化主空間區分度、雜波極化相關性以及極化通道數是影響檢測性能的主要極化域因素.最后,通過仿真驗證了文中結論的正確性.

1 信號模型

圖1為運動平臺陣列雷達觀測示意圖,其中,va為平臺速度,H為平臺運動高度,α和β分別表示雜波地塊相對陣面的方位角和俯仰角,θcone表示載機速度矢量對于雜波的空間錐角.設雷達含有M個收/發通道,每個通道均含有一對正交極化天線同時發射和接收水平/垂直極化信號.為便于分析,假設陣列在空間上均勻排布(間距為d).

圖1 運動平臺雷達觀測示意圖

設指定距離單元中含有運動目標,雷達回波數據可表示為

其中,Nc為該距離單元內的雜波地塊數;?為Kronecker乘積運算符;gi和γi分別為第i個雜波地塊的等效增益和等效后向散射系數,在短時脈沖積累時間內可認為是固定值;x、xt和n分別為回波信號、目標信號以及噪聲信號;sip、sis和sit分別為第i個雜波地塊的極化導向矢量、空間導向矢量和時間導向矢量.

在空間陣元位置均勻分布的情況下,雜波的時間導向矢量和空間導向矢量分別為

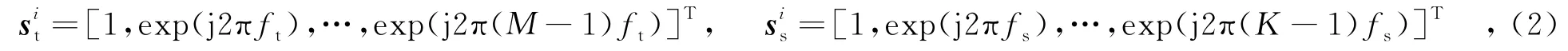
,分別為空間頻率和多普勒頻率;λ為波長;prf為脈沖重頻.

雷達極化回波的全極化數據矢量可表示為[SHH,SHV,SVH,SVV]T,且在單站后向散射情況下根據互易定理,有SHV=SVH.設雜波為完全極化波,其全極化數據的導向矢量可表示為

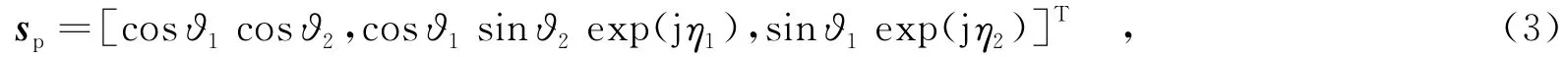
在雜波回波為非完全極化波時(實際中的大多數情況),需使用相關矩陣描述其極化特性.雜波數據x的聯合相關矩陣可表示為

其中,r和ε分別為通道HV、通道VV與通道HH數據平均功率的比值,ρ1、ρ2、ρ3和η1、η2、η3分別為通道HV與HH、通道VV與HH、通道VV與HV的平均相關系數和平均相位差.

2 極化空時自適應處理

首先從輸出信雜噪比的角度建立分析模型,接著對比極化空時自適應算法與空時二維處理的性能,最后通過分析指出幾種主要的影響因素.

2.1 分析模型

極化空時全維自適應處理的權矢量wopt為

其中,k為非零常數,s0為目標的極化空時聯合導向矢量,s0=sp?st?ss.下面通過輸出信雜噪比(SCNR)分析系統的檢測性能,其在雜波相關矩陣確知時的計算式為其中,表示目標信號的能量.

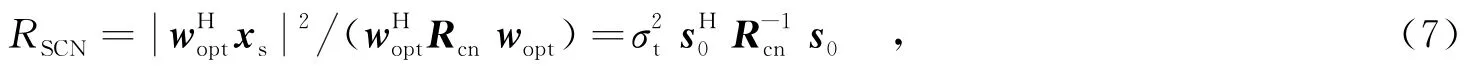
為分析信雜噪比的計算式,首先對Rp和Rst分別進行特征分解,并將特征值按照從大到小的順序進行排列,即

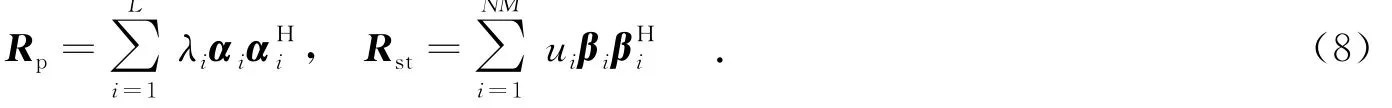
設目標的極化空時導向矢量s0=sp?sst,輸出的信雜噪比可表示為

由于Rp為半正定矩陣,且tr(Rp)=1,故其特征值在0～1范圍內.另一方面,對稱矩陣的特征向量之間相互正交,且Rp的特征向量和sp均是模1的,因此,則有

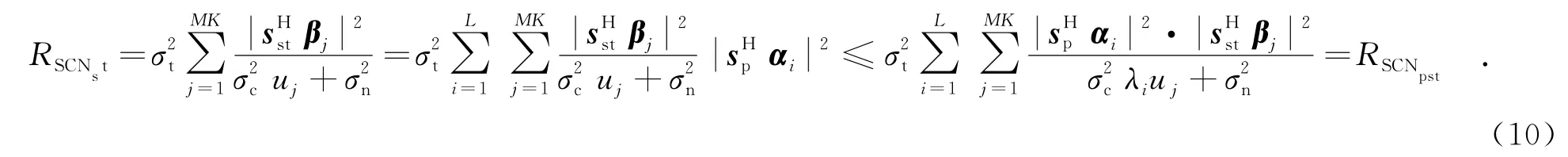
故利用極化信息可以改善空時自適應處理的檢測性能.

2.2 影響因素

下面從輸出信雜噪比計算式的角度指出幾類主要的影響因素.類似于雜波的空時相關矩陣,雜波極化相關矩陣同樣由極化主空間與副空間構成,通常也稱為信號子空間與噪聲子空間.當雜波為完全極化波時,其主空間維數為1,副特征值為0;當雜波為部分極化波時,主特征值隨著相關性的下降而降低,而副特征值逐漸上升;當雜波為完全非極化波時,其特征空間無主、副之分.現實中大部分目標的極化相關性大于0.因此,這里僅考慮完全極化波與部分極化波.

設雜波極化相關矩陣Rp由維數為b的主空間Um與維數為L-b的副空間Uau組成,即

其中,主、副特征值λm,i和λa,i的大小與雜波極化相關性有關.

輸出信雜噪比為

設目標極化導向矢量sp與第i個極化特征向量αi的夾角為χi,sp向極化主空間Um投影的角度為φ,同時設sp在主空間Um和副空間Uau的投影矢量與對應空間內各個特征向量之間的夾角為φi.根據余弦的計算定理,可以得到

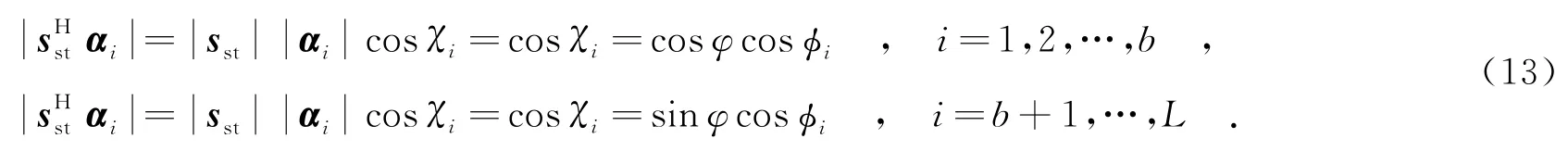
則輸出信雜噪比可表示為

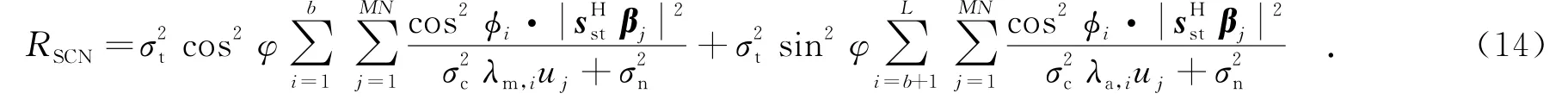
由該式可知,極化投影角φ、特征值λm,i和λa,i以及極化通道數L共同影響極化空時自適應算法的檢測性能,分別對應于目標極化導向矢量與雜波極化主空間的區分度、雜波相關性以及自適應處理使用的極化通道數據的個數.特別地,當雜波回波為完全極化波時,極化投影角即為目標與雜波的極化導向矢量的角度差.空時二維區分度對自適應處理的影響因素分析類似,具體詳見文獻[11].

3 仿真結果

為驗證上述結論,使用機載仿真數據對極化空時自適應檢測性能進行分析.仿真參數如下:設發射信號波長為0.1 m(S波段內);俯仰向陣列經合成之后,天線在方位向等效為8個間距半波長的收發通道,并相干處理12個脈沖;平臺運動速度為150 m/s;脈沖重復頻率為1 500 Hz.仿真采用全極化數據:HH通道下累積的信噪比和雜噪比分別為15 dB和30 dB;雜波HH通道和VV通道的能量一致,而相位超前90°,HV通道和HH通道的相位一致,而能量低10 dB;同時假設目標的兩個同極化通道的數據能量一致,且比交叉極化高5 dB.

3.1 極化通道數

規定目標的全極化導向矢量sp,使得極化投影角度為45°,雙極化采用HH/VV通道數據進行仿真,如圖2所示.可以看到,隨著極化通道個數的增加,檢測性能逐漸上升.這一現象主要有兩方面原因:(1)信號積累的能量與通道個數成正比.(2)極化濾波增加了處理器的自由度.對比兩幅圖像可以發現,隨著極化相關系數的增加,慢速目標的檢測性能得到了改善.

圖2 不同極化相關系數下的輸出信雜噪比(SCNR)曲線

3.2 雜波極化通道間的相關性

從最小可檢測速度MDV、平均輸出信雜噪比損失兩個方面考察雜波極化通道間相關性對檢測性能的影響.為有效分析損失值的大小,定義平均輸出信雜噪比損失為

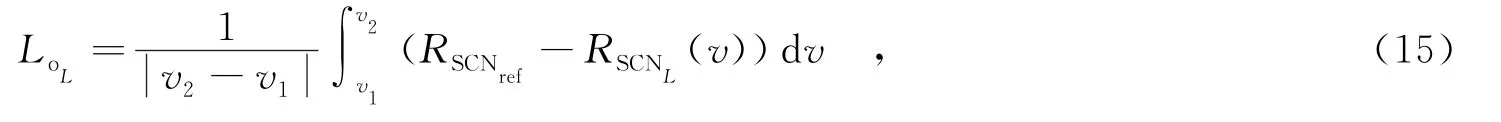
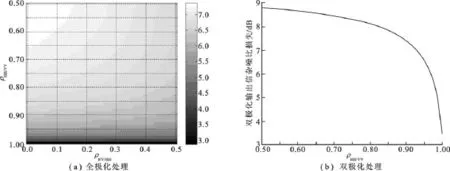
圖3 輸出信雜噪比的損失

其中,RSCNref為參考的輸出功率,RSCNL為感興趣速度區間v1～v2內的輸出信雜噪比.

設系統感興趣的測速區間為0～20 m/s,目標極化導向矢量sp的設置同上,仿真結果如圖3所示.

可以看到,同極化相關性ρHH/VV的增加可顯著改善系統的輸出RSCN,對于全極化數據,隨著ρHV/VV的增加,系統的RSCN損失也呈現降低趨勢,但是由于相關系數值偏低,其影響較小.

3.3 極化區分度

設全極化數據的同極化相關系數為0.9,交叉極化相關系數為0,fdn表示歸一化的多普勒頻率仿真結果.由圖4可以看到,隨著目標與雜波極化信號子空間投影角度的增加,極化空時自適應算法的性能逐漸上升;對于低速目標,較高的極化投影角可大幅度地提高檢測性能,有效消除空時二維處理中的盲速區間,提高了系統的目標檢測能力.

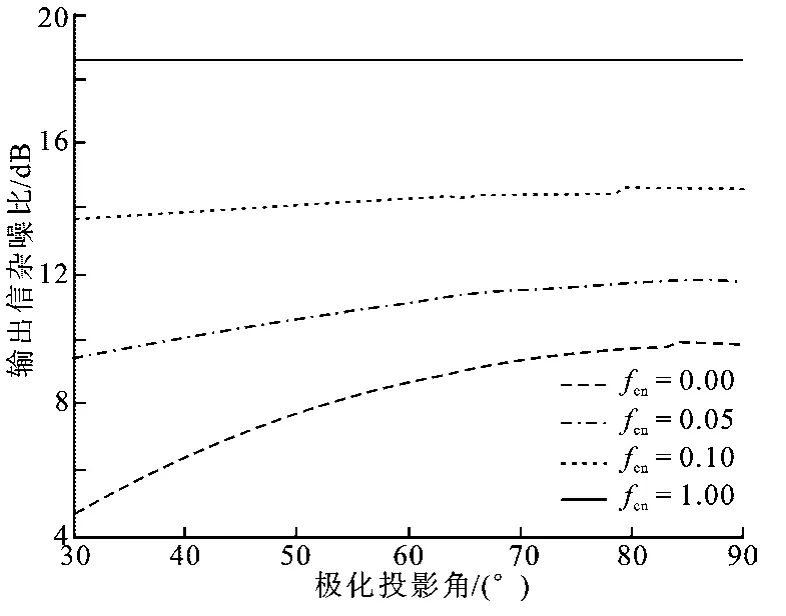
圖4 全極化處理輸出信雜噪比的曲線

4 結束語

基于對輸出信雜噪比值計算式的分析,指出了極化空時自適應算法的主要影響因素,證明了增加極化域信息可以改善系統的檢測性能.仿真結果表明,當目標的多普勒頻率較低時,極化投影角度的增加,可以顯著地改善系統的動目標檢測性能;而當目標的速度較大時,此時空時域已經有很好的檢測效果.增加極化區分度獲得的改善有限,但是隨著極化通道個數、極化相關性的增加,檢測性能可以進一步獲得提升.

[1]Melvin W L.A STAP Overview[J].IEEE Transactions on Aerospace and Electronic Systems,2004,19(1):19-35.

[2]Cristallini D,Burger W.A Robust Direct Data Domain Approach for STAP[J].IEEE Transactions on Signal Processing,2012,60(3):1283-1294.

[3]李彩彩,廖桂生,朱圣棋,等.一種多普勒后處理的STAP方法研究[J].西安電子科技大學學報,2009,36(2):240-244. Li Caicai,Liao Guisheng,Zhu Shengqi,et al.Study of Post-doppler Processing STAP Method[J].Journal of Xidian University,2009,36(2):240-244.

[4]Ginolhac G,Forster P,Pascal F,et al.Performance of Two Low-rank STAP Filters in a Heterogeneous Noise[J]. IEEE Transactions on Signal Processing,2013,61(1):57-61.

[5]Wang Na,Hu C B,Zhao L J,et al.Polarimetric SAR Target Detection Based on Polarization Synthesis[C]//IEEE International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2012:5899-5902.

[6]Kelly E J.An Adaptive Detection Algorithm[J].IEEE Transactions on Aerospace and Electronic System,1986,22(1): 115-127.

[7]Park H R,Kwak Y K,Wang H.Efficient Joint Polarization Space-time Processor for Nonhomogeneous Clutter Environments[J].Electronics Letters,2002,38(25):1714-1715.

[8]Park H R,Wang H.Adaptive Polarization-space-time Domain Radar Target Detection in Inhomogeneous Clutter Environments[J].IEE Proceedings-Radar,Sonar and Navigation,2006,153(1):35-43.

[9]Wu D J,Xu Z H,Zhang L,et al.Polarization-space-time Adaptive Processing for Clutter Suppression in Airborne Radar Systems[C]//Second International Conference on Digital Manufacturing and Automation.Piscataway:IEEE Computer Society,2011:855-858.

[10]Delcora P,Pierfrancescro L,Tullio B.Adaptive Polarimetric Target Detection with Coherent Radar[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(4):1194-1220.

[11]Wang H,Cai L J.On Adaptive Spatial-Temporal Processing for Airborne Surveillance Radar Systems[J].IEEE Transactions on Aerospace and Electronic Systems,1994,30(3):660-669.

(編輯:齊淑娟)

Performance analysis of the polarization-space-time adaptive processing

DU Wentao,LIAO Guisheng,YANG Zhiwei
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

By the utilization of the additional polarized information,the minimum detectable velocity could be improved for space time adaptive processing under the polarimetric radar system.In this paper,the performance of polarization space time adaptive processing is analyzed and compared with the traditional space-time adaptive processing based on the output signal to clutter plus noise ratio,and the primary affecting factors of three dimensional processing are indicated.A preliminary result against an airborne simulation data verifies the conclusion.

polarimetric radar;target detection;polarized signal processing;space-time adaptive processing

TN959.1

A

1001-2400(2014)01-0001-05

10.3969/j.issn.1001-2400.2014.01.001

2013-03-21 < class="emphasis_bold">網絡出版時間:

時間:2013-09-16

長江學者與創新團隊發展計劃資助項目(IRT0954);國家自然科學基金資助項目(60901066);國家部委預研基金資助項目(9140xxxx001);中央高校基本科研業務費專項資金資助項目(K5051302007)

杜文韜(1989-),男,西安電子科技大學博士研究生,E-mail:duwentao_xd@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.1_031.html