入侵雜草優化算法用于陣列天線方向圖綜合

劉 燕,焦永昌,張亞明,王新寬

(1.西安電子科技大學天線與微波技術重點實驗室,陜西西安 710071; 2.西北工業大學電子信息學院,陜西西安 710129)

入侵雜草優化算法用于陣列天線方向圖綜合

劉 燕1,焦永昌1,張亞明2,王新寬1

(1.西安電子科技大學天線與微波技術重點實驗室,陜西西安 710071; 2.西北工業大學電子信息學院,陜西西安 710129)

針對目前智能優化算法在處理具有多零點、凹口和低旁瓣等要求的復雜陣列天線方向圖綜合問題時易出現收斂速度慢或局部最優的問題,引入一種新型入侵雜草優化算法,并在此基礎上設計了一種自適應入侵雜草優化算法.新算法既提高了收斂速度,又平衡了全局和局部搜索能力.與同類算法相比,新算法在處理復雜陣列天線方向圖綜合問題中性能更佳,具有更高的收斂速度和計算精度.

陣列天線;方向圖綜合;入侵雜草優化算法;零點;凹口;低旁瓣

陣列天線方向圖綜合的目的是確定陣列天線的某些參數,使天線陣的輻射特性滿足給定的要求.由于方向圖綜合問題中的目標函數和約束條件大部分呈多參數、非線性、不可微甚至不連續的特點,使得傳統的基于梯度尋優技術的數值優化方法無法有效地求得工程滿意解.而各種智能優化算法,比如遺傳算法(GA)、粒子群算法(PSO)及其改進算法等[1-7],以其良好的魯棒性在陣列天線方向圖的綜合設計中得到了廣泛的應用.2006年,Mehrabian等[8]提出了一種新穎的智能優化算法——入侵雜草優化算法(Invasive Weed Optimization,IWO).該算法模擬雜草種子在自然界的擴散、生長、繁殖和競爭性消亡的基本過程,具有很強的魯棒性和自適應性,能夠有效地收斂于問題的最優解.

由于入侵雜草優化算法收斂速度快,程序設計簡單、易實現,因此很快就引起國外從事天線研究領域的學者的關注.Roshanaei等[9]把入侵雜草優化算法用于陣列天線自適應波束形成,并且與遺傳算法進行比較,入侵雜草優化算法所需的計算時間更少,得到的代價函數也更小;Roy等[10]則把入侵雜草優化算法用于非均勻圓形天線陣的設計,并驗證了該算法在收斂速度、魯棒性等方面優于遺傳算法和粒子群算法.

入侵雜草優化算法有一個非常突出的特點,是通過一個滿足正態分布的方差來產生子代,該方差的大小決定了父代和子代的距離大小.在傳統的入侵雜草優化算法中,方差σ的值隨進化代數的增加而單調減小,這樣的結果在進化后期,隨著進化代數的增加,σ越來越小,使得產生的新種子就分布在父代種子很近的范圍內,容易造成局部最優.針對上述不足之處,結合陣列天線方向圖綜合問題的特點,為了使入侵雜草優化算法適應于更復雜的目標函數,比如在降低旁瓣電平的同時還要求在指定位置形成深零點或凹口,筆者設計了一種自適應入侵雜草算法(Adaptive Invasive Weed Optimization,AIWO).該算法中的標準差除了隨進化代數增加而變小以外,還隨每個個體的適應度函數值變化.這樣不僅能提高收斂速度,而且有助于幫助新產生的種子跳出局部最優,在提高收斂速度的同時,更好地平衡了全局收斂和局部收斂.

1 算法描述

1.1 入侵雜草優化算法基本原理

入侵雜草優化算法與一般進化算法(比如遺傳算法和粒子群算法)相比,其主要特點是:在進化過程中,種群中的所有個體都有機會產生新的個體,適應度越高的個體產生的新個體數量越多.這種機制在加強較優個體周圍局部搜索的同時兼顧種群多樣性,更符合自然進化法則.

入侵雜草優化算法的實現可以通過初始化、生長繁殖、空間分布、競爭性生存法則這4個步驟實現.

第1步 初始化種群.在D維搜索空間,隨機產生一組初始解X=(X1,X2,…,XM),其中M為初始種群個數(小于最大種群數Pmax).

第2步 生長繁殖.每個雜草個體可產生的種子數根據其適應度值由最小值到最大值線性變化.對于最大化問題,每個雜草個體可產生的種子數為

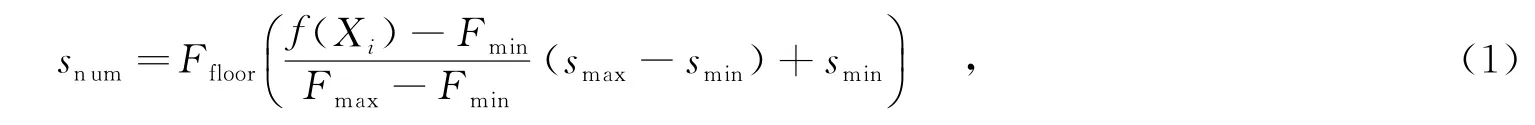
其中,Fmax和Fmin為該代進化中最大、最小適應度值,smax和smin為可產生的最大種子數和最小種子數,f(Xi)為第i個雜草個體的適應度值,Ffloor(x)函數表示向下取整.

第3步 空間分布.空間分布體現了算法的隨機性和適應性,產生的種子在D維搜索空間,以正態分布N(0,σ2)隨機分散在父代雜草附近.第i個雜草產生的第s個種子的位置為

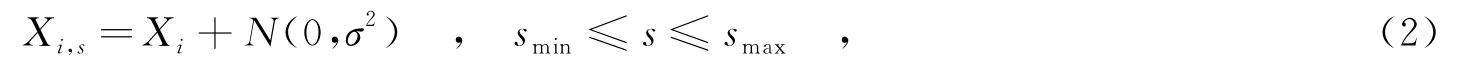
其中,σ為標準差.隨著進化代數的增加,σ逐漸減小,其變化規律為

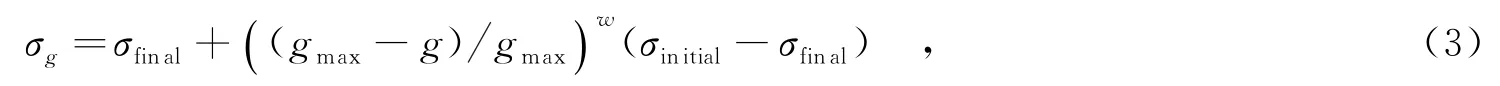
其中,g為進化代數,σinitial,σfinal為初始和最終標準差,w為非線性調節因子.式(3)確保隨著進化代數的增加,在較遠區域產生種子的可能性非線性減小.在迭代初期,較大的σ使得產生的種子分布在父代較遠范圍;在迭代后期,較小的σ使得產生的種子分布在父代較近范圍.這樣的方式使得算法逐漸完成從全局搜索到局部搜索的轉變,有利于提高算法的速度和效率.

第4步 競爭性生存法則.當種群數超過最大值Pmax時,所有個體按照其適應度函數排序,對于最大化問題,對排序后的個體按適應度值由大到小依次選出Pmax個個體,作為該代進化最終保留下來的種群,其余個體被淘汰.保留下來的種群就可以進入下一輪進化,直到達到最大進化代數.

經過上述4個步驟得到的新種子不一定都在解空間內.為了保證所得解的有效性,筆者采用吸收邊界法,即如果產生的某個種子超出預設的搜索邊界,則取邊界值.

1.2 自適應入侵雜草優化算法

在基本入侵雜草優化算法中,σ只隨進化代數的增加而變小,以完成算法從全局搜索到局部搜索的轉變.而在某一代中σ的值是不變的,這顯然不利于算法收斂.尤其是在進化后期,隨著進化代數的增加,σ的值越來越小,這樣產生的新種子只能分布在父代個體的附近,容易陷入局部最優.在此,筆者設計了一種更為合理有效的方法——自適應入侵雜草優化算法,即在某一代中σ的值根據其適應度值大小進行變化,表示為

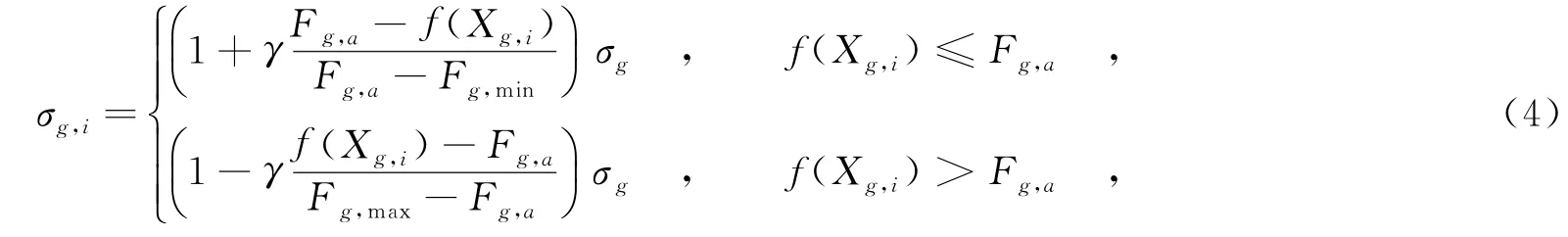
其中,Fg,a、Fg,max和Fg,min是該代進化中的平均適應度值、最大適應度值和最小適應度值;γ為縮放因子,控制標準差的變化范圍,一般取0到1之間,本文取值為0.5.

可以看出,在某一代中,當某個個體的適應度值等于該代進化的平均適應度值時,其標準差就等于基本入侵雜草算法的標準差.對于最大化問題,在某一代中,適應度值大的個體標準差較小,這樣有利于種子分布在較優個體周圍;而適應度值小的個體標準差較大,有利于在較遠范圍內分布更優的種子,這有助于提高算法的收斂速度.另一方面,該自適應標準差σg,i的取值范圍為[1-γ,1+γ]σg,在進化的下一代某個個體的標準差很可能大于上一代某個個體的標準差,而不是式(3)所描述的下一代的標準差一定小于上一代的標準差,有效地幫助產生的新種子跳出局部最優,在加快收斂速度的同時,有效地平衡了全局和局部搜索能力.

1.3 自適應入侵雜草優化算法的偽碼表示

自適應入侵雜草優化算法如下:

2 陣列天線方向圖綜合

考慮一個2N單元等距均勻直線陣,且陣元為各向同性單元.設電流相位均為零(邊射陣),而電流幅度中心對稱,其以分貝表示的歸一化陣因子為[7]

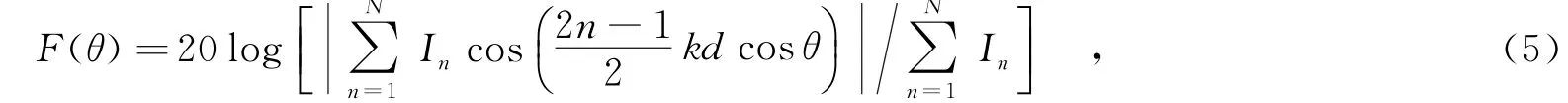
其中,In為第n個陣元的電流幅度;d為陣元間的間距;k=2π/λ,k為波數,λ為自由空間波長;θ為射線方向與陣列軸線之間的夾角.

適應度函數的設計考慮兩方面因素:一方面要求旁瓣電平低于一定值LTPS,另一方面要求在給定的N0個方向θi(i=1,2,…,N0)形成深度為LNLV的深零點.因此,適應度函數可定義為

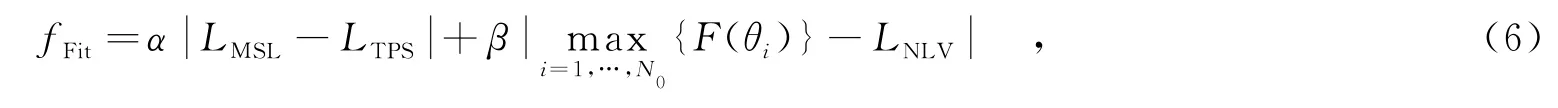
其中,LTPS為目標峰值旁瓣電平,LMSL為最大相對旁瓣電平.權重系數α和β的取值視情況而定.

在編程過程中,為了避免出現適應度函數值為零的情況,用式(7)把式(6)表示的最小化問題轉換成最大化問題,即

3 仿真結果

為了驗證自適應入侵雜草算法的有效性,通過3組不同的仿真實例,對式(5)所描述的電流幅度中心對稱的直線陣進行方向圖綜合設計,其中,2N=20,陣元間距d=λ/2,主瓣寬度2θ0=20°,參數設置見表1.并與入侵雜草優化算法、遺傳算法和粒子群算法所得結果進行比較.

表1 自適應雜草優化算法參數設置

3.1 綜合低旁瓣方向圖

綜合要求:最大旁瓣電平低于-40 d B.適應度函數選擇式(7),α=1,β=0.仿真得到的方向圖和進化曲線如圖1所示.其中入侵雜草優化算法和自適應入侵雜草算法均進化50代,遺傳算法和粒子群算法分別進化500代和300代.由進化曲線可以看出,自適應入侵雜草算法的進化速度明顯優于入侵雜草優化算法,在進化到第33代時已經完全收斂,適應度函數值達到1.同時,自適應入侵雜草算法得到的方向圖最大旁瓣電平也最低,為-40.001 6 dB,而入侵雜草優化算法、遺傳算法和粒子群算法算法得到的最大旁瓣電平分別為-39.998 5 dB、-34.562 1 dB、-39.004 dB.由此可見,自適應入侵雜草算法的進化速度和精度都明顯優于另外3種算法.優化得到的激勵電流幅值見表2.

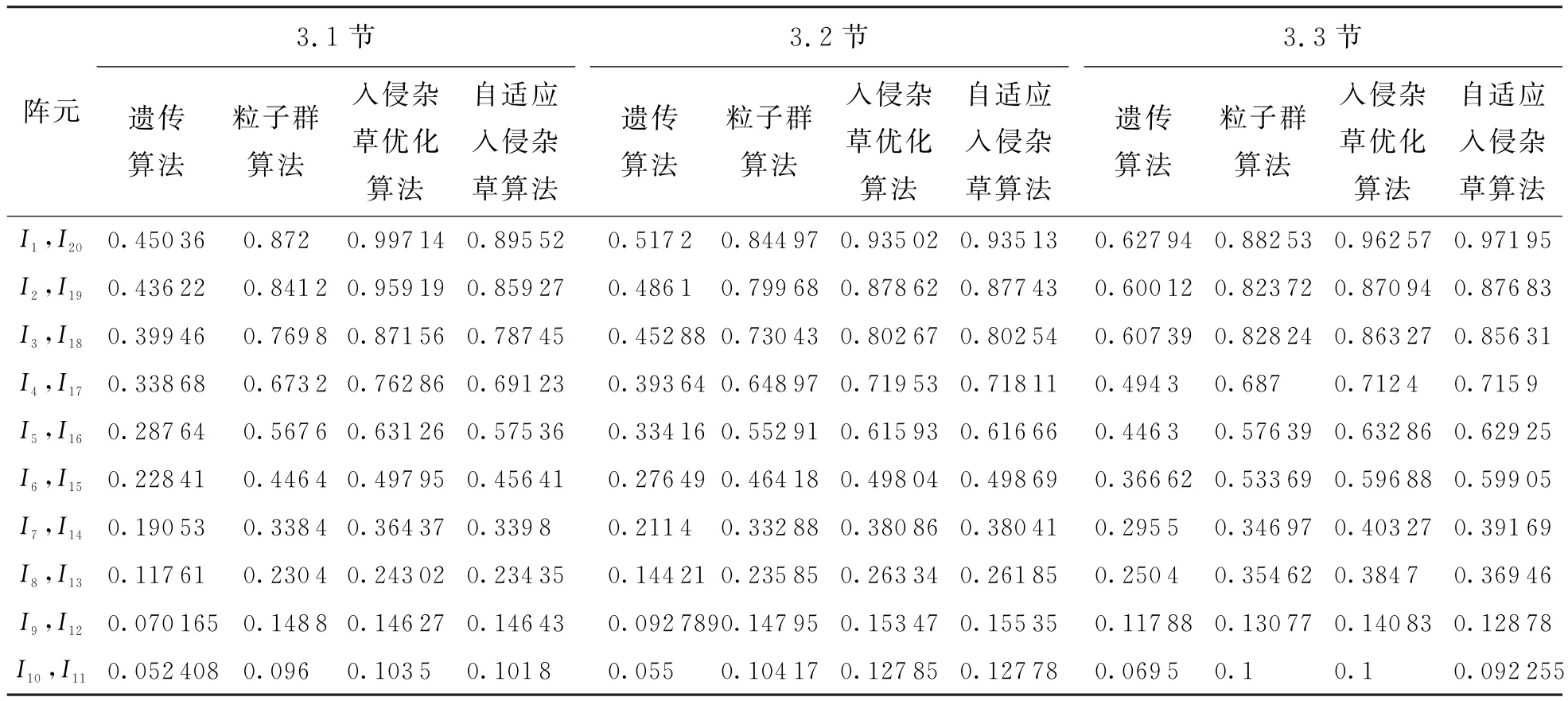
表2 3個實例中用4種算法優化得到的激勵電流幅值

3.2 綜合具有深零點的方向圖

綜合要求:要求在最大旁瓣電平低于-35 dB的同時,在60°、70°和80°的位置形成低于-80 dB的深零點,式(6)中取α=0.8,β=0.2.4種算法均進化1 000次,仿真得到的方向圖如圖2所示.入侵雜草優化算法優化得到的最大旁瓣電平和最大深零點分別為-36.264 6 d B、-80.117 2 d B,而自適應入侵雜草算法得到的最大旁瓣電平和最大深零點為-36.268 8 dB、-89.657 4 dB.自適應入侵雜草算法在保證最大旁瓣電平基本不變的情況下,使最大深零點電平降低了9.540 2 d B.由圖2還可以看出,自適應入侵雜草算法得到的方向圖其最大旁瓣電平和最大深零點均低于遺傳算法(-34.106 3 dB和-79.824 1 dB)和粒子群算法(-35.889 5 dB和-79.824 1 d B)的,驗證了自適應入侵雜草算法在進化速度、精度和處理復雜目標函數等方面具有較為顯著的優勢.優化得到的激勵電流幅值見表2.

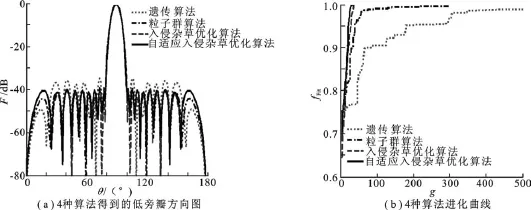
圖1 方向圖和進化曲線

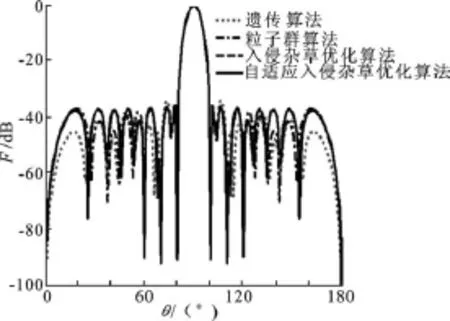
圖2 4種算法得到的深零點方向圖

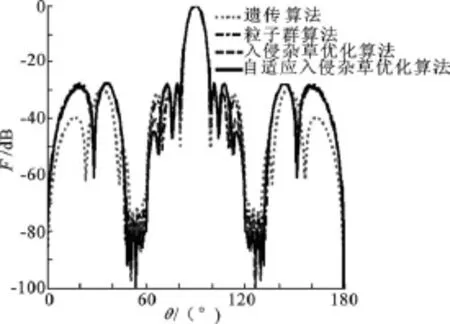
圖3 4種算法得到的凹口方向圖

3.3 綜合具有凹口的方向圖

綜合要求:要求在最大旁瓣電平低于-27 d B的同時,在50°到60°之間形成低于-80 d B的凹口.4種算法均進化1 000次,仿真得到的方向圖如圖3所示.自適應入侵雜草算法得到的最大旁瓣電平和最大凹口電平為-28.000 2 dB和-79.960 8 d B,與入侵雜草優化算法相比,分別降低了0.404 9 d B和4.205 4 d B.由圖3可以看出,自適應入侵雜草算法得到的結果的最大旁瓣電平和最大凹口電平也均低于遺傳算法(-27.473 7 dB和-66.975 7 dB)和粒子群算法(-27.528 7 d B和-72.621 1 dB)的.優化得到的激勵電流幅值見表2.由此可以看出:在相同條件下,自適應入侵雜草算法得到了更理想的結果,進一步驗證了該算法在處理復雜目標函數時的明顯優勢.

4 總 結

針對現有智能優化算法在處理復雜方向圖綜合問題時易出現收斂速度慢和早熟收斂的問題,在引入新型智能優化算法——入侵雜草優化算法的同時,設計了自適應入侵雜草算法.該算法采用自適應標準差產生新的種子,根據每個父代個體適應度值的大小來確定其產生的新種子分布在距離父代多遠的距離范圍,該改進算法在提高全局搜索速度和效率的同時,有效地平衡了全局和局部搜索能力.由第3節的仿真實例可以看到,筆者所提算法在收斂速度和精度上均優于同類其他算法,整體性能更佳,更適用于天線方向圖綜合問題,值得推廣應用.

[1]Liao W P,Chu F L.Array Pattern Synthesis with Null Steering Using Genetic Algorithms By Controlling Only the Current Amplitudes[J].International Journal of Electronics,1999,86(4):445-457.

[2]Mandal D,Majumdar A,Kar R,et al.Thinned Concentric Circular Array Antennas Synthesis Using Genetic Algorithm [C]//IEEE Student Conference on Research and Development.Piscataway:IEEE,2011:194-198.

[3]Shihab M,Najjar Y,Dib N,et al.Design of Non-uniform Circular Antenna Arrays Using Particle Swarm Optimization [J].Journal of Electrical Engineering,2008,59(4):216-220.

[4] 王維博,馮全源.粒子群算法在陣列天線方向圖綜合中的應用[J].西安電子科技大學學報,2011,38(3):175-180. Wang Weibo,Feng Quanyuan.Application of PSO Algorithm in Pattern Synthesis[J].Journal of Xidian University,2011,38(3):175-180.

[5] 劉瑞斌,鄢澤洪,孫從武.PSO和GA在陣列天線波束賦形中的應用[J].西安電子科技大學學報,2006,33(5):797-799. Liu Ruibin,Yan Zehong,Sun Congwu.Application of PSO and GA in Beamforming of an Array Antenna[J].Journal of Xidian University,2006,33(5):797-799.

[6]Khairy M,Fayek M B,Hemayed E E.PSO2:Particle Swarm Optimization with PSO-based Local Search[C]//IEEE Congress of Evolutionary Computation.Piscataway:IEEE,2011:1826-1832.

[7] 馬云輝.基于遺傳算法的唯相位控制方向圖零點生成[J].微波學報,2001,17(2):41-46. Ma Yunhui.Null Steering Using Genetic Algorithms By Controlling Only the Current Phases[J].Journal of Microwaves,2001,17(2):41-46.

[8]Mehrabian A R,Lucas C.A Novel Numerical Optimization Algorithm Inspired From Weed Colonization[J].Ecological Informatics,2006,1(3):355-366,.

[9]Roshanaei M,Lucas C,Mehrabian A R.Adaptive Beamforming Using a Novel Numerical Optimization Algorithm[J]. IET Microwaves,Antennas&Propagation,2009,3(5):765-773.

[10]Roy G G,Das S,Chakraborty P,et al.Design of Non-Uniform Circular Antenna Arrays Using a Modified Invasive Weed Optimization Algorithm[J].IEEE Transactions on Antennas and Propagation,2011,59(1):110-118.

(編輯:郭 華)

Application of the invasive weed optimization algorithm to the pattern synthesis of array antennas

LIU Yan1,JIAO Yongchang1,ZH ANG Yaming2,WANG Xinkuan1
(1.Science and Technology on Antenna and Microwave Lab.,Xidian Univ.,Xi’an 710071,China; 2.School of Elec.&Info.,Northwestern Polytechnical Univ.,Xi’an 710129,China)

For overcoming the problem of slow convergence speed and local optimum by using the existing intelligent optimization algorithms in the pattern synthesis of antenna arrays with nulls,notches and sidelobe reduction,a novel invasive weed optimization(IWO)algorithm is presented,and an adaptive IWO is designed to improve the convergence speed and make a balance between the global and local searching ability.Simulation results show that,compared with other existing algorithms,the proposed algorithm performs better,with higher convergence speed and better computation accuracy.

array antennas;pattern synthesis;invasive weed optimization;nulls;notches;sidelobe reduction

TN821+.91

A

1001-2400(2014)01-0029-05

10.3969/j.issn.1001-2400.2014.01.006

2012-10-15 < class="emphasis_bold">網絡出版時間:

時間:2013-09-16

國家自然科學基金資助項目(61201022)

劉 燕(1982-),女,西安電子科技大學博士研究生,E-mail:liuyan_xidian@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.37_002.html