General Solutions of Thermoelastic Plane Problems of Two－Dimensional Quasicrystals

Zhang Liangliang（張亮亮），Yang Lianzhi（楊連枝），Yu Lianying（余蓮英），Gao Yang（高陽）＊＊

1.College of Science，China Agricultural University，100083，Beijing，P.R.China；2.College of Engineering，China Agricultural University，100083，Beijing，P.R.China

1 Introduction

An increasing number of quasicrystals（QCs）with good thermal stability make thermoelasticity analyses for QCs more and more important.Furthermore，in view of the fact that QCs have a potential to be used as the components in drilling and nuclear storage facilities［1］，it′s very necessary to study the influence of the temperature for QCs.For the general solutions of QCs，thermal effort is always beyond the scope of the studies.Wang et al［2］derived the general solutions for thermoelastic problems of two－dimensional（2D）decagonal QCs by using the complex variable technique.Li et al［3］inferred the general solutions for three－dimensional（3D）thermoelastic problems of one－dimensional（1D）hexagonal QCs.For plane piezothermoelastic medium，Xiong et al［4］and Kumar et al［5］deduced the general steady state solution，respectively.The general solutions for 2Dplane thermoelastic problems，such as 2Ddecagonal QCs have not been attempted.The purpose of this paper is to system－atically investigate the thermoelastic plane problems of two－dimensional decagonal QCs.

2 Basic Equations

2DQCs refer to a 3Dsolid structure with two quasi－periodic arrangement directions and one periodic direction.For 2DQCs with Cartesian coordinate system（x1，x2，x3），we assume that x1－x2is the quasi－periodic plane and x3is the periodic direction.Due to the mathematical complexities，3Dproblems of 2DQCs are difficult to be analytically solved.In order to explicitly study the phonon－phason interaction，only plane elasticity theory is considered in this paper.Since the x1－x2plane is the quasi－periodic plane，we can employ the x1－x3plane or the x2－x3plane for the study of plane phonon－phason coupling phenomena.In the present work we chose the former，so this problem can be decomposed into an anti－plane problem and an in－plane problem.In this paper，only in－plane problem is considered，the field variables are independent of x2，such that?2＝0，where?j＝?／?xj.For 2Ddecagonal QCs，the point groups 10mm，1022，1m2，10／mmm belong to Laue class 14.In the absence of body forces，the general equations governing the plane 2Ddecagonal QCs can be written as

where uiand w1denote phonon and phason displacements in the physical and perpendicular spaces，respectively；σijandεijare the phonon stresses and strains；H1jand w1jare the phason stresses and strains；C11，C13，C33，C44represent the elastic constants in phonon field；K1，K4are the elastic constants in phason field；Ris the phonon－phason coupling elastic constants；β1，β3are the thermal constants；Tis the variation of the temperature.By virtue of the parallel method proposed by Gao et al［6］，the equilibrium equation can be represented with uiand w1as follows

Assuming that the thermoelastic loading changes slowly with time and without consideration of the rate of entropy，the uncoupled thermoelastic theory of QCs is adopted in the following analysis.In a steady－state，the heat conductivity equation is

where k11and k33are thermal conductivity coefficients.In a similar manner to transversely isotropic elasticity［7］and piezoelasticity［8］，the balance Eq.（4）and heat conductivity Eq.（5）for the problem is

where the vector U＝［u1，u3，w1，T］T（the superscript″T″denotes the transpose）；Ais a 4×4differential operator matrix，such as

In terms of Eq.（6），it seems to be extremely difficult to find the solution by means of direct integration due to the complexity of the equations.Furthermore，a decomposition and superposition procedure is manipulated to simplify the complicated governing equation by introducing a displacement function.

3 General Solutions of Problem

By virtue of the operator analysis technique［6，9－10］，the general solutions of the problem will be developed.Introduce a 4×4differential operator matrix B，components Bijof which are″algebraic complement minors″of Ain Eq.（4），i.e.

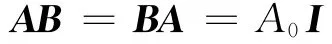
where A0is the″determinant″of the differential operator A，I the unit matrix.Then the general solution of Eq.（5）can be expressed as

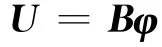
where the displacement function vectorφsatisfies the following equation

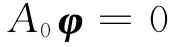
The″determinant″A0of Ayields

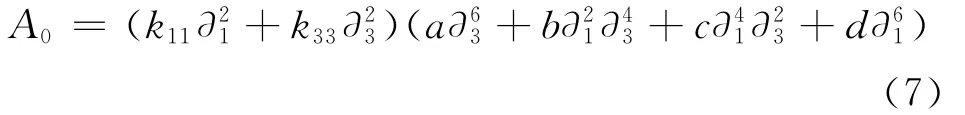
where

Now introduce a displacement function H，which satisfies

where the quasi－harmonic differential operatorsare expressed as

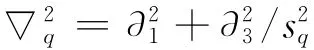
If the index qis taken to be 1，2or 3，three sets of general solutions with T＝0will be obtained，which are actually the elastic general solutions without thermal effect.Taking q＝4，we can obtain

or

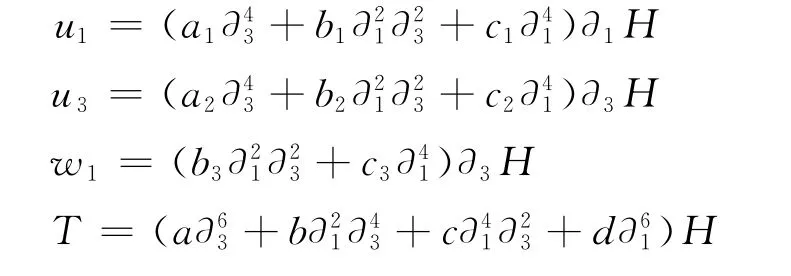
where

By utilizing the generalized Almansi′s theorem［11］the displacement function Hcan be expressed by four quasi－harmonic equations Hqin five distinct forms as

where Hqsatisfy the following second－order equations

in which the upper case subscript Qtakes the same number as the corresponding lower case q，but with no summation convention.Therefore，the eighth－order Eq.（8）has been replaced with four quasi－harmonic equations.

In this paper，only the case of distinct values sqis concerned.Then，the general solution can be written as

Here setα＝1，2，3，where

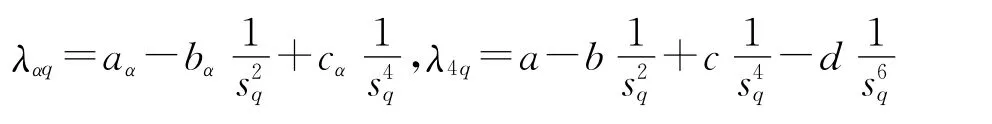
For further simplification，assume that

From Eqs.（8，11），it can be seen thatψqsatisfy the following equations

Therefore，the general solutions of the thermoelastic plane problems of 2Ddecagonal QCs can be expressed in terms of the four quasi－harmonic functionsψqas follows

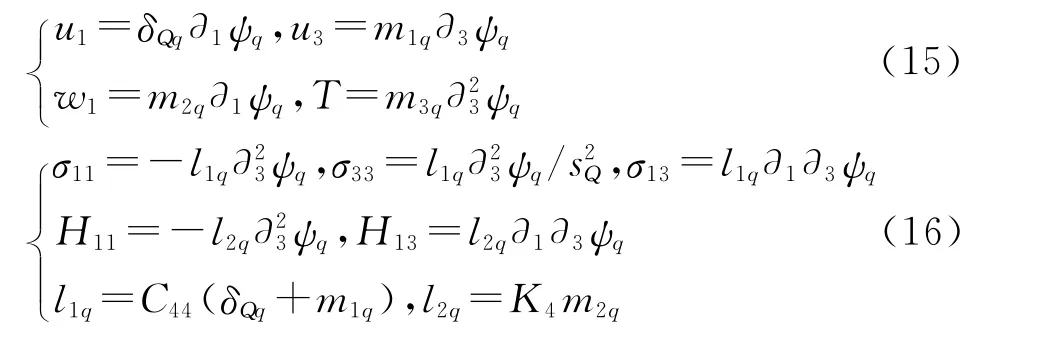
whereδQqis the Kronecker Delta symbol，m1q＝λ2q／λ1Q，m2q＝λ3q／λ1Q，m3q＝λ4q／λ1Q.When q＝1，2，3，m3q＝0.

Eqs.（15－16）are the general solutions of this thermoelastic plane problem in terms of displacement functionsψq.If boundary conditions are given，the analytic solutions can be obtained for the boundary value problems.

4 Steady Point Heat Source in Semiinfinite Plane

Consider a semi－infinite QC plane x3≥0 whose quasi－periodic direction is the x1－axis，and whose periodic direction is x3－axis as in Fig.1.A point heat source His applied at the point（0，h）in 2DCartesian coordinates（x1，x3）and the surface（x3＝0）is free.Based on the general solutions，the thermal field in the semi－infinite QC plane is derived in this section.

The boundary conditions on the surface x3＝0are

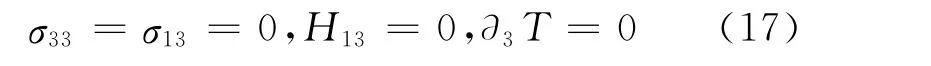
For future reference，a series of denotations are introduced as follows

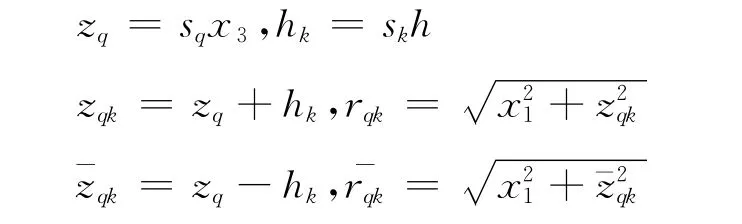
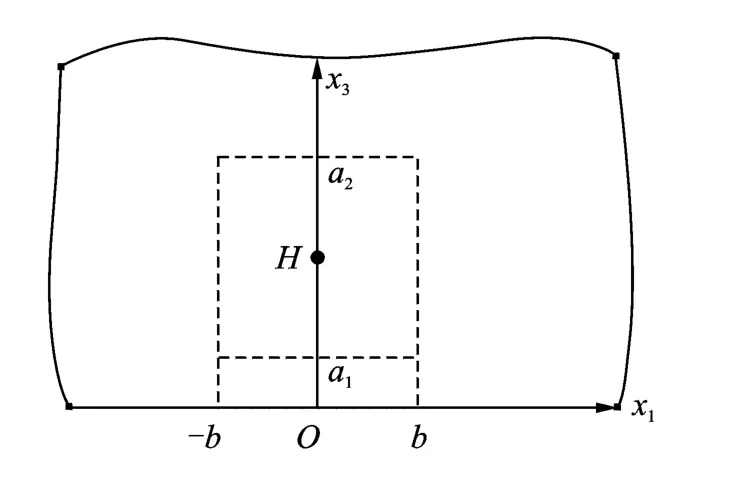
Fig.1 Semi－infinite QC plane applied by apoint source H

Introduce the following harmonic functions

where Aqand Aqkare twenty constants to be determined.Substituting Eq.（18）into Eqs.（15－16），the expressions of the coupled field are as follows

Considerating the continuity on plane x3＝h for u3，σ13and H13yields

Substituting Eq.（16）into Eq.（22），by virtue of Eq.（21），Eq.（22）can be simplified into one equation

When the phonon，phason and thermal equilibrium for a cylinder of a1≤x3≤a2（0＜a1＜h＜a2）and 0≤r≤b are considered，three additional equations can be obtained

Substituting Eq.（20）into Eqs.（24－25）and integrating，we can obtain

where

Thus，Eq.（24）is satisfied automatically.A4can be determined by Eq.（27）as follows

Finally，when the coupled field on the surface x3＝0is considered，substituting general solutions Eqs.（15－16）into boundary conditions Eq.（17）and using s4＝we can obtain

Thus，twenty constants Aqand Aqkcan be determined by twenty equations，including Eqs.（23，29－30）.

5 Conclusions

On the basis of the operator method and the introduction of the displacement function H，the general solutions of thermoelastic plane problems of 2Ddecagonal QCs are first presented.The introduced displacement function Hhas to satisfy an eighth－order partial differential equation.Owing to complexity of the higher order equation，it is difficult to obtain rigorous analytic solutions directly and not applicable in most cases.Based on the Almansi′s theorem，and by virtue of a decomposition and superposition procedure，the general solution is further simplified in terms of four quasi－harmonic functionsψq.Considering that the characteristic roots s2qare distinct，the obtained general solutions of 2Ddecagonal QCs are in simple forms which are conveniently applied.As an application of the general solution，for a steady point heat source in a semi－infinite QC plane，the closed form solutions are presented by the four harmonic functions.

The general solutions are very convenient to be used to study the inhomogeneity and defect problems of 2Ddecagonal QCs.These also provide basis to judge the rationality of the solutions by the finite element method or the boundary element method.The analysis method in this paper can also be used to solve the more complicated thermoelastic plane problems of 2DQCs.

Acknowledgements

This work was supported by the National Natural Science Foundation of China（11172319）；the Chinese Universities Scientific Fund（2011JS046，2013BH008）；the Opening Fund of State Key Laboratory of Nonlinear Mechanics；the Program for New Century Excellent Talents in University（NCET－13－0552）；the National Science Foundation for Post－doctoral Scientists of China（2013M541086）.

［1］ Hu Chengzheng，Yang Wenge，Wang Renhui，et al.Quasicrystal symmetry and physical properties［J］.Progress in Physics，1997，17（4）：345－375.（in Chinese）

［2］ Wang，X，Zhang J Q.A steady line heat source in a decagonal quasicrystalline half－space［J］.Mechanics Research Communications，2005，32（4）：420－428.

［3］ Li X Y，Li P D.Three－dimensional thermo－elastic general solutions of one－dimensional hexagonal quasicrystal and fundamental solutions［J］.Physics Letters A，2012，376（26／27）：2004－2009.

［4］ Xiong S M，Hou P F，Yang S Y.2－D green′s functions for semi－infinite orthotropic piezothermoelastic plane［J］.Ultrasonics，Ferroelectrics and Frequency Control，2010，57（5）：1003－1010.

［5］ Kumar R，Chawla V.General steady－state solution and green′s function in orthotropic piezothermoelastic diffusion medium［J］.Archives of Mechanics，2012，64（6）：555－579.

［6］ Gao Y，Zhao B S.A general treatment of three－dimensional elasticity of quasicrystals by an operator method［J］.Physical Status Solidi（b），2006，243（15）：4007－4019.

［7］ Hu H.On the three－dimensional problems of the theory of elasticity of a transversely isotropic body［J］.Scientia Sinica，1953，9（2）：145－151.

［8］ Ding H J，Chen B，Liang J.General solutions for coupled equations for piezoelectric media［J］.International Journal of Solids and Structures，1996，33（16）：2283－2298.

［9］ Wang M Z，Wang W.Completeness and nonuniqueness of general solutions of transversely isotropic elasticity［J］.International Journal of Solids and Structures，1995，32（3）：501－513.

［10］Wang W，Shi M X.On the general solutions of transversely isotropic elasticity［J］.International Journal of Solids and Structures，1998，35（25）：3283－3297.

［11］Ding H J，Cheng B，Liang J.On the Green′s functions for two－phase transversely isotropic piezoelectric media［J］.International Journal of Solids and Structures，1997，34（23）：3041－3057.