橡膠減振支座動態性能仿真分析研究

方建輝，丁智平，卜繼玲，黃友劍，李 飛，白曉鵬

（1. 湖南工業大學 機械工程學院，湖南 株洲 412007 ；2. 株洲時代新材料科技股份有限公司，湖南 株洲 412007）

橡膠減振支座動態性能仿真分析研究

方建輝1，丁智平1，卜繼玲2，黃友劍2，李 飛1，白曉鵬1

（1. 湖南工業大學 機械工程學院，湖南 株洲 412007 ；2. 株洲時代新材料科技股份有限公司，湖南 株洲 412007）

基于Mooney-Rivlin、Ogden 3階和Van der Waals三種橡膠超彈材料本構模型，考慮載荷頻率、載荷幅值、載荷均值諸因素影響,分別建立風力發電機橡膠減振支座有限元模型，對橡膠減振支座動態性能進行數值模擬。通過橡膠支座動態承載測試實驗，分析不同橡膠材料本構模型對橡膠彈性元件仿真精度的影響。橡膠減振支座仿真分析與動態承載實驗結果的誤差分析顯示，壓剪變形載荷工況適合選用Van der Waals模型；Mooney-Rivlin模型適合中、小變形載荷工況；Ogden 3階模型則更適合較大變形載荷工況。為提高橡膠彈性元件有限元仿真精度，應根據所受載荷工況選用合適的橡膠材料本構模型。

橡膠；有限元；本構模型；彈性剛度；誤差

1 研究背景

橡膠作為一種獨特的彈性阻尼材料被廣泛應用于各種隔振系統中，其承受動態載荷的性能決定橡膠彈性元件減振性能的好壞，因此模擬仿真橡膠材料的動態性能，對于防止彈性元件的剛度失效是非常必要的。由于橡膠具有幾何及材料雙重非線性，給橡膠產品的力學性能分析帶來了很大的困難，且采用傳統的解析方法時遇到大應變非線性問題總是引入過多的假設。近年來基于數值算法的各種大型有限元分析軟件的出現，為解決橡膠產品大應變非線性問題提供了有效途徑，其分析結果也逐漸應用到橡膠產品設計中。

橡膠材料力學性能的研究涉及多方面，如疲勞[1-5]，本構關系[6]等。目前，橡膠隔振器的靜態性能計算方法的研究相對成熟，采用有限元方法[7-9]進行分析是較為常用的方法。為工程應用預測，采用的材料本構模型，可分成3類[10]：1）基于分子統計熱力學理論的本構模型；2）以應變不變量表示的應變能密度函數；3）以主伸長率表示的應變能函數。用統計熱力學法研究彈性體材料可追溯到1940年，該方法試圖從硫化橡膠的理論模型中得出它的彈性本質[11]。Millard F. Beatty等人[12]進一步提出了準Wu和Van der Giessen模型，可統一推導出多種非高斯統計模型，并提出以變形不變量表示的唯象法本構模型與分子統計熱力學法本構模型之間的一些聯系；A·N·詹特[13]在《橡膠工程：如何設計橡膠配件》一書中詳盡地描述了橡膠材料的本構關系。基于上述工作，在橡膠減震元件動態性能方面也取得了一些成果，等人[14]對一種炭黑填充橡膠襯套的徑向和軸向動態性能進行了實驗，研究了徑向和軸向的頻率和幅值相關性，并基于實驗結果建立了徑向和軸向彈性剛度數學模型；C. R. Brackbill等人[15]研究了橡膠類阻尼材料在簡單剪切狀態下小應變幅值和頻率相關性；J. M. Horton[16]基于經典彈性理論，對一種橡膠彈性襯套建立了徑向彈性剛度預測模型。

橡膠彈性元件目前主要采用靜剛度設計準則進行產品設計，不能確保產品承受動載荷時的工作可靠性，因而預測橡膠彈性元件在實際工況下動態承載性能，成為工程實際中需要解決的問題。本文利用ABAQUS有限元軟件，分別使用3種不同的橡膠超彈材料本構模型，對不同實驗工況的風力發電機橡膠減振支座進行動態承載性能模擬仿真，并與實驗結果進行對比分析，評估有限元仿真分析的精度，為橡膠彈性元件工程設計提供更加可靠的設計依據。

2 橡膠材料本構模型

橡膠是一種同時具有超彈性和黏彈性的高聚物，力學性質兼具有不可恢復的永久形變和可恢復的彈性形變，對橡膠元件進行有限元分析，首先要選擇合適的本構模型以及獲取準確的材料參數。

2.1 超彈性本構模型及參數擬合

株洲時代新材料科技股份有限公司選送了橡膠材料試樣樣本至美國Axel實驗室，進行了單軸拉伸、平面拉伸和等軸拉伸實驗，獲得了較為精確的應力應變實驗數據，實驗數據見圖1。

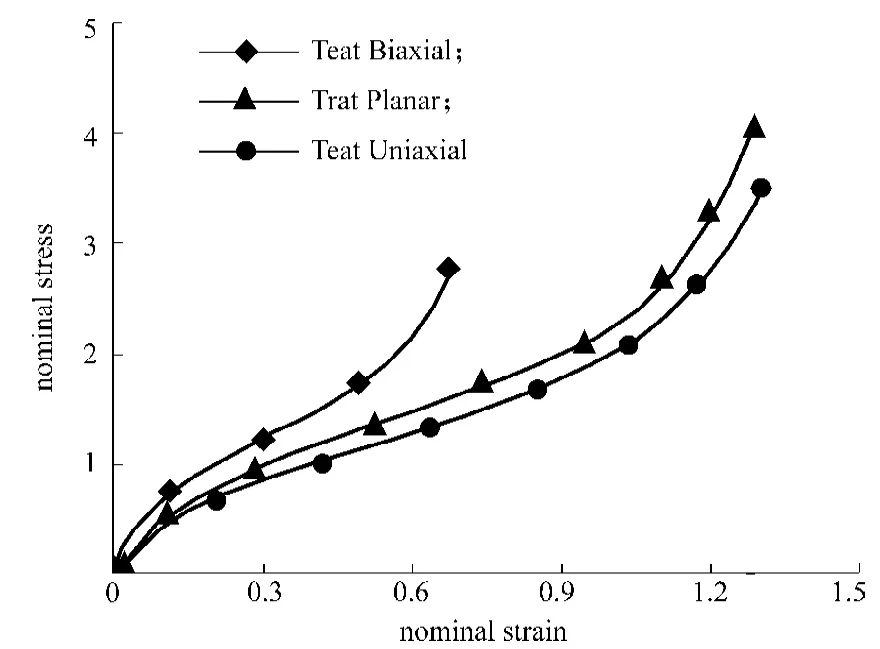
圖1 橡膠材料靜態基礎實驗數據Fig.1 Static experimental data of rubber material

橡膠是一種各向同性、體積近似不可壓縮的高分子材料，其非線性彈性一般采用超彈性本構模型描述，最常用的有Mooney-Rivlin、Ogden、Van der Waals。3種模型中，Mooney-Rivlin本構模型在小應變和中等應變時可以較好地模擬材料特性，但不能夠表示對于應力應變曲線的大應變部分“陡升”行為；Ogden本構模型適合于分析拉、壓工況下大變形行為；Van der Waals本構模型則具有對壓剪應變狀態的良好模擬能力。

1）Mooney-Rivlin本構模型

M-R本構模型是最簡單的超彈本構模型，未知精確參數的材料通常采用M-R模型，其應變勢能為

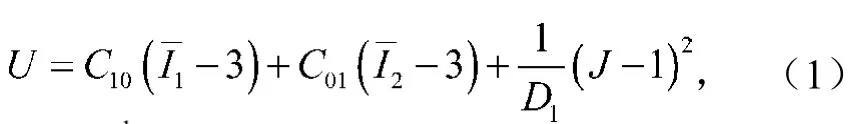
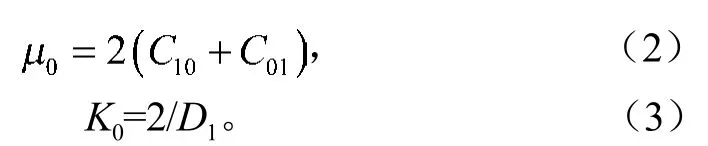
采用M-R模型進行參數擬合，其擬合效果如圖2所示。

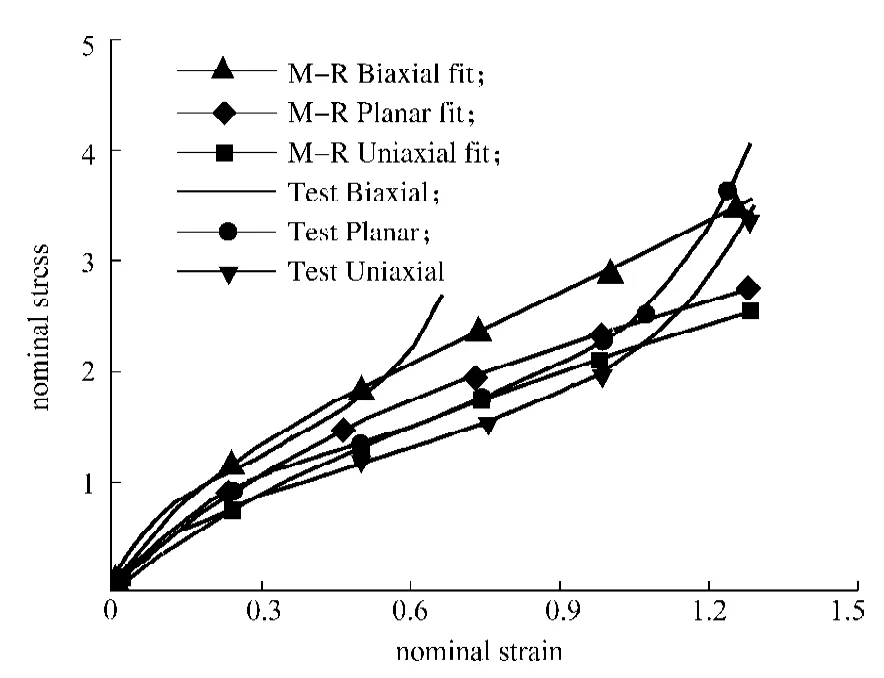
圖2 M-R本構模型參數擬合Fig.2 Parameters fitting of M-R constitutive model

2） Ogden本構模型

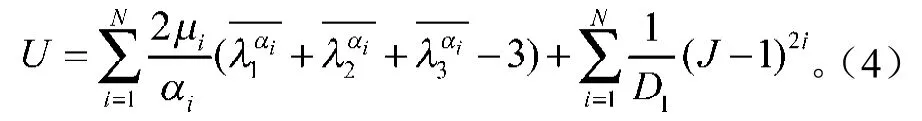
采用Ogden模型進行擬合，效果見圖3。

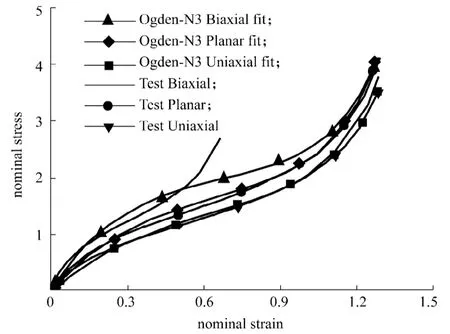
圖3 Ogden本構模型參數擬合Fig.3 Parameters fitting of Ogden constitutive model

3）Van der Waals本構模型為

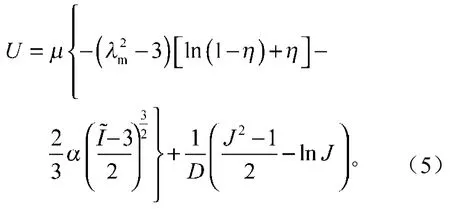
采用Van der Waals模型進行擬合，效果見圖4。

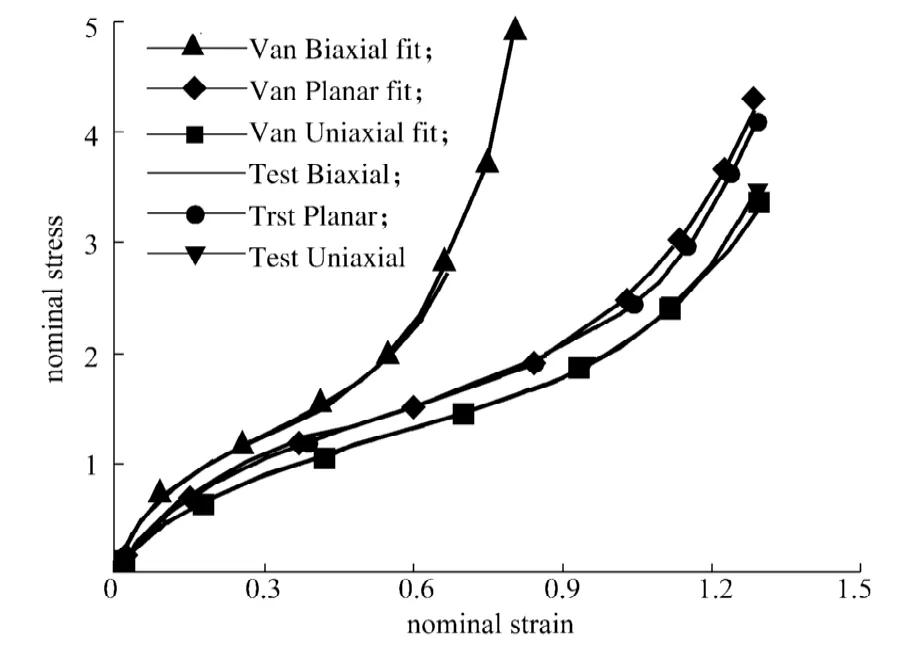
圖4 Van der Waals本構模型參數擬合Fig.4 Parameters fitting of Van der Waals constitutive model

本文分別選擇上述3種本構模型，利用ABAQUS軟件對橡膠材料靜態基礎實驗數據進行擬合，獲得了其橡膠超彈性本構參數，見表1。

表1 超彈性參數Table1 Hyperelastic parameters of constitutive models

2.2 黏彈性試驗及參數擬合

橡膠材料的黏彈性試驗包括應力松弛試驗或蠕變試驗。從力學角度來說，應力松弛試驗與蠕變試驗是等效的，因此測試橡膠的黏彈特性，選擇兩者之一即可。本文選擇應力松弛試驗來擬合黏彈性參數，其松弛模量[17]為

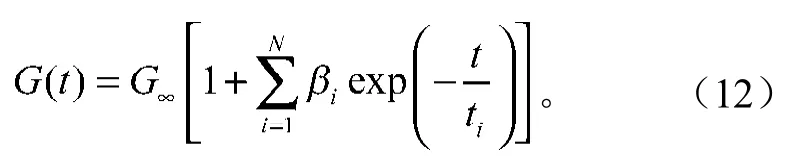
表2 黏彈性參數Table2 Parameters of viscoelasticity

3 橡膠支座有限元模型

由于該橡膠支座結構較為復雜（見圖5），而有限元分析精度與網格質量密切相關，采用ABAQUS進行分析計算時，計算效率與網格量有關，為確保分析精度，提高計算效率，最終建立的軸對稱單元有限元模型如圖6所示。其中橡膠部分單元數量為169個，采用C3D8H單元模擬，總計單元數970個；芯軸與外套采用C3D8R 單元模擬。橡膠部分材料參數見表1，芯軸與外套均為金屬材料，彈性模量E為210e3，泊松比為0.3，密度7.8e-9t/mm。

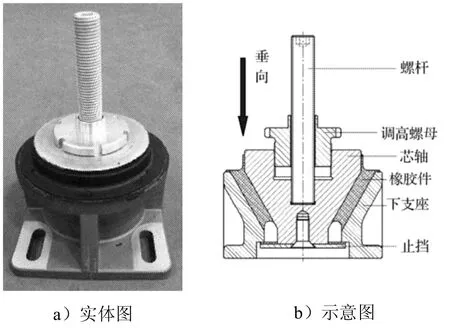
圖5 橡膠支座結構Fig.5 The rubber bracket structure

在模型中芯軸的對稱中心線上端處建立1個參考點RP-1，將芯軸一個面與該參考點耦合，參考點上施加垂向載荷，外套外表面約束固定，如圖6所示。

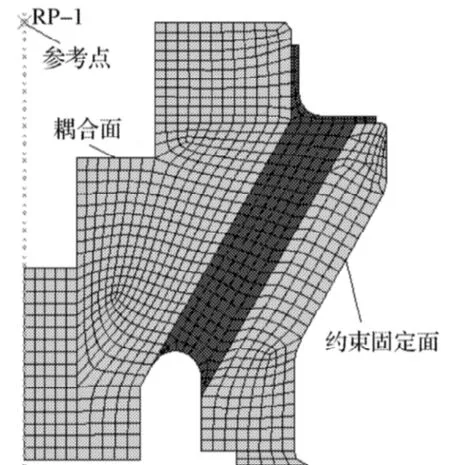
圖6 橡膠支座有限元模型Fig.6 Finite element model of rubber brackets

4 橡膠支座動態承載性能實驗

4.1 實驗

橡膠彈性支座在承載過程中不僅需要滿足靜態剛度的要求，同時也要滿足動態性能要求。本文的產品試樣（見圖5a）采用硬度為邵氏55°的填充橡膠材料，金屬構架材料選用45號鋼。為了消除試件加工時產生的內應力，產品試樣須在(23±2)℃環境溫度下放至少24h后進行試驗。試驗采用Instron8802液壓伺服動態儀，動態性能測試實驗在株洲時代新材股份有限公司進行。產品彈性剛度實驗具體情況見圖7，實驗工況見表3。

圖7 橡膠支座動態性能實驗Fig.7 Dynamic performance experiment of rubber brackets

橡膠支座動態承載性能實驗按照表3設計實驗工況進行，共25個實驗。

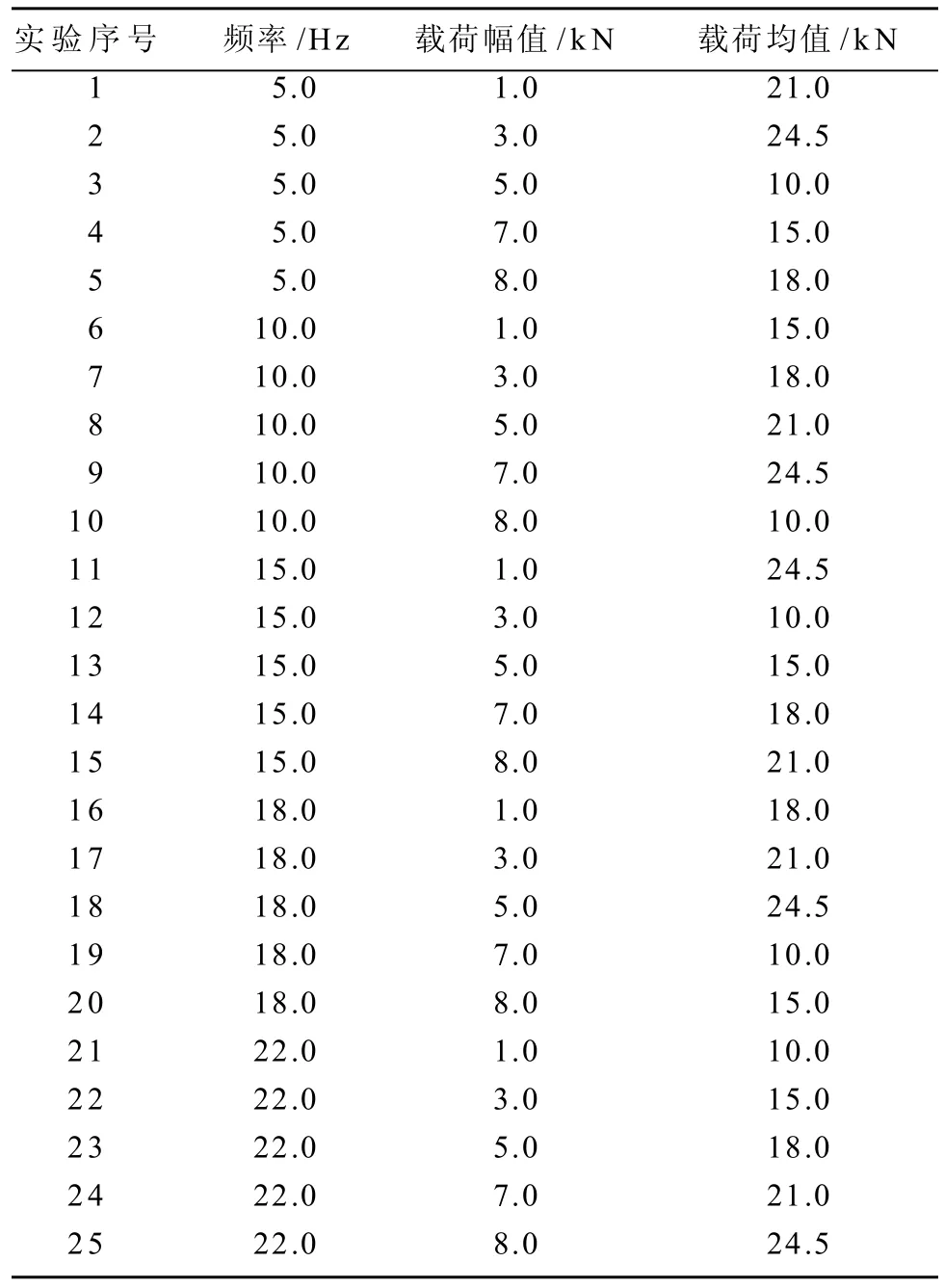
表3 實驗工況Table3 Loads of test

4.2 彈性剛度計算理論

有限元分析所獲得的力-位移數據，通過橢圓法[18]，可以獲得仿真彈性剛度與阻尼因子，其剛度模型[17]如式（8），即

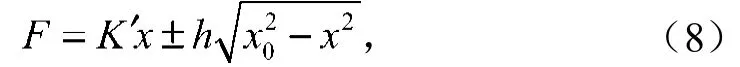
式中：K′表示彈性剛度；

h表示K′與阻尼因子 的乘積。

將式（8）利用二維圖進行表示，如圖8所示。

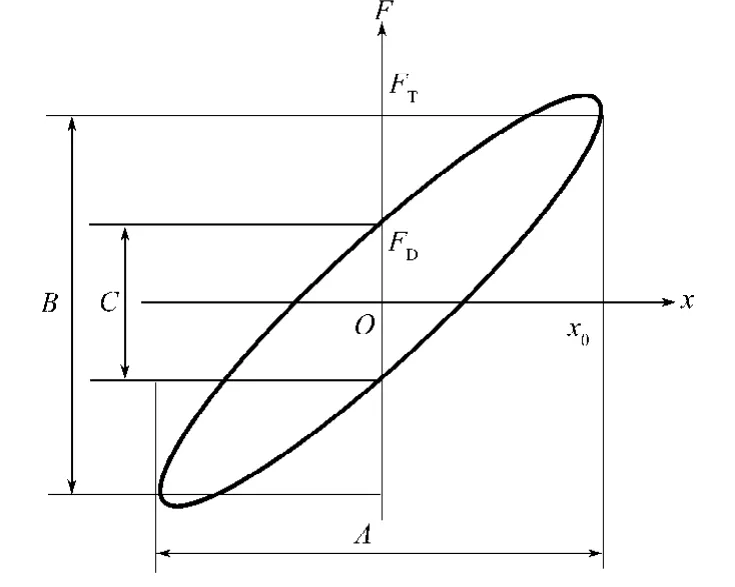
圖8 力-位移的滯回曲線Fig.8 Hysteresis curve of force - displacement

K′可通過式（9）計算得到：

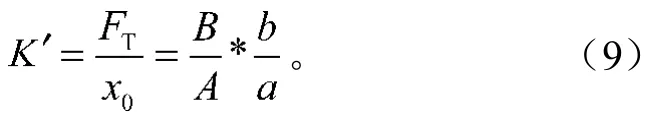
式中：A為最大位移在遲滯回線上的雙幅長度；

B為與最大位移對應的傳遞力在遲滯回線上的雙幅長度；

a為橢圓圖上橫坐標單位長度代表的位移；

b為橢圓圖上縱坐標單位長度代表的力；

FT為載荷達到最大值時的傳遞力。

式中：C表示位移為零時傳遞力在遲滯回線上的雙幅長度；

FD表示位移為零時對應的傳遞力。

4.3 仿真結果與實驗驗證

根據每種實驗工況下的有限元分析結果，結合式（9）～（10）計算彈性剛度與阻尼因子值，用表2動態性能實驗結果進行驗證，所得結果見圖9～10。

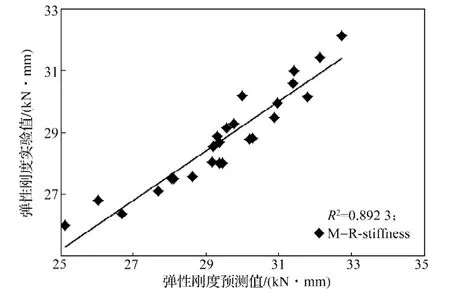
圖9 M-R模型的彈性剛度仿真與實驗結果Fig.9 Elastic stiffness simulation of M-R model and experimental results

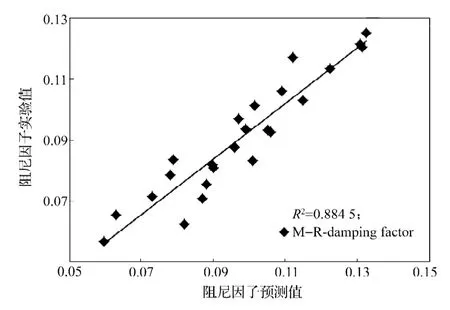
圖10 M-R模型的阻尼因子仿真與實驗結果Fig.10 Damping factor simulation of M-R model and experimental results

驗證結果顯示，三種模型彈性剛度預測值與阻尼因子均呈一定的相關性。采用M-R本構模型的仿真預測結果集與實驗數據較為接近，具有良好相關性（相關系數見圖9～10）。

Ogden3階模型的仿真預測結果相關性較低（相關系數見圖11～12）。

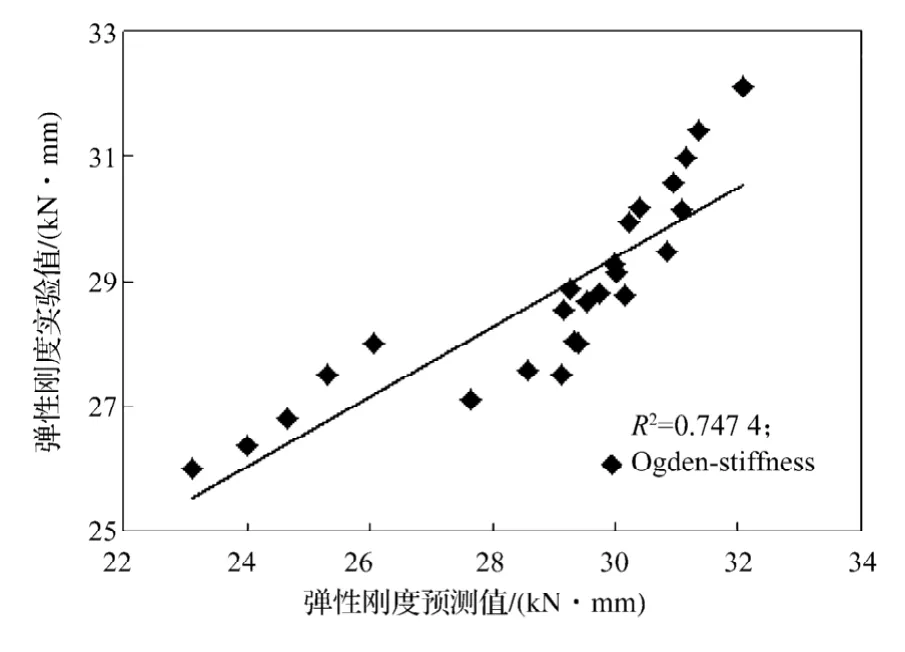
圖11 Ogden模型的彈性剛度仿真與實驗結果Fig.11 Elastic stiffness simulation of Ogden model and experimental results

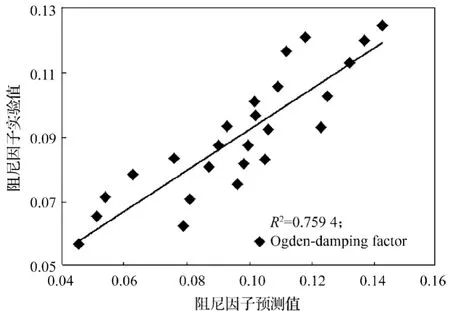
圖12 Ogden模型的阻尼因子仿真與實驗結果Fig.12 Damping factor simulation of Ogden model and experimental results

Van der Waals本構模型的仿真預測結果與實驗結果相關性最好（相關系數見圖13～14）。

從本構模型的適用工況類型分析，不同的本構模型適合的承載工況不同，選擇合適的本構模型對于提高有限元仿真精度有很大的影響。

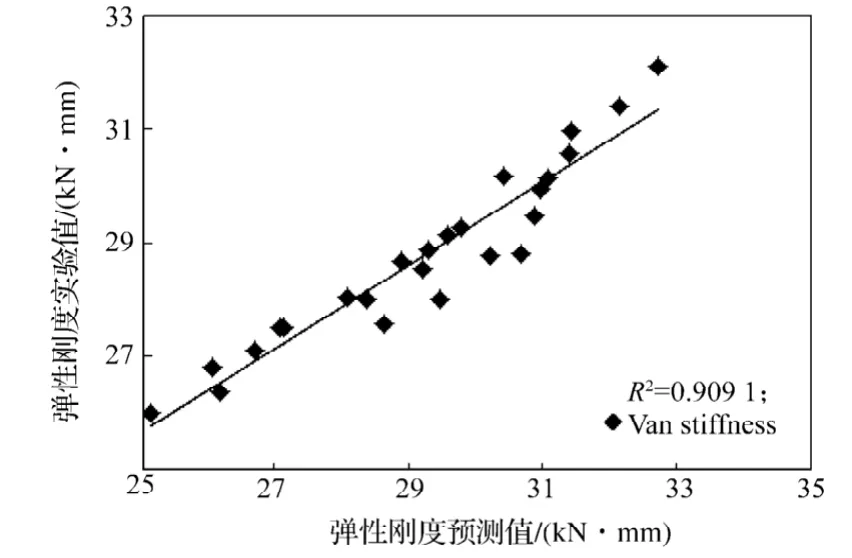
圖13 Van der Waals模型的彈性剛度仿真與實驗結果Fig.13 Elastic stiffness simulation of Van der Waals model and experimental results

圖14 Van der Waals模型的阻尼因子仿真與實驗結果Fig.14 Damping factor simulation of Van der Waalsmodel and experimental results

5 誤差分析

將3種本構模型進行仿真分析的結果見表4。

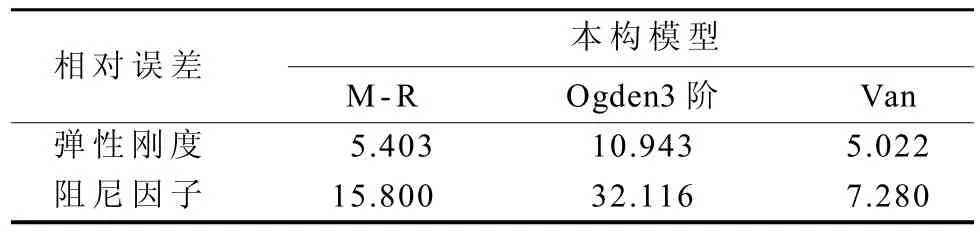
表4 仿真誤差分析Table4 Simulation error analysis %

由表4與實驗值對比可知，Van der Waals與Mooney-Rivlin模型仿真結果均比較理想，其中Van der Waals模型精度較高，而用Ogden3階模型則誤差較大。由于本文橡膠支座承受壓縮剪切變形載荷，處于小變形范圍，因此合適壓縮剪切變形模擬的Van der Waals模型精度較高，適合于中、小變形模擬的Mooney-Rivlin模型也能獲得良好仿真結果，而比較合適大變形模擬的Ogden3階模型仿真效果較差。由此可見，針對橡膠產品的載荷工況，選取合適的本構模型尤為重要。

6 結論

1）分別基于3種不同橡膠超彈性本構模型，建立了風力發電機橡膠減振支座有限元模型，對其動態承載性能進行有限元數值模擬，應用動載荷下的力—位移滯回曲線數據，結合彈性剛度計算理論得到橡膠支座彈性剛度與阻尼因子預測值。

2）進行橡膠減振支座承受壓剪載荷動態承載性能測試實驗，并將實驗值與仿真預測值進行對比分析。實驗值與預測值的相關性分析和誤差分析表明：對于本文分析的橡膠減振支座，Van der Waals模型仿真精度較好，其次是Mooney-Rivlin模型，Ogden3階模型較差。

3）選用橡膠本構模型進行有限元仿真，應考慮橡膠彈性元件承受的載荷工況。對于壓剪變形載荷工況，適合選用Van der Waals模型；Mooney-Rivlin模型適合中、小變形載荷工況；而Ogden3階模型則更適合較大變形載荷工況。

[1] 丁智平，陳吉平，宋傳江，等. 橡膠彈性減振元件疲勞裂紋擴展壽命分析[J]. 機械工程學報，2010，46(22)：58-64. Ding Zhiping，Chen Jiping，Song Chuanjiang，et al. Analysis of Fatigue Crack Growth Life for Rubber Vibration Damper[J]. Journal of Mechanical Engineering，2010，46 (22)：58-64.

[2] 楊榮華，丁智平，卜繼玲，等. 橡膠球鉸疲勞裂紋擴展壽命預測[J]. 湖南工業大學學報，2013，27(2)：48-53. Yang Ronghua，Ding Zhiping，Bu Jiling. Prediction of Fatigue Crack Growth Life for Rubber Bushing[J]. Journal of Hunan University of Technology，2013，27(2)：48-53.

[3] Mars W V，Fatemi A. A Literature Survey on Fatigue Analysis Approaches for Rubber[J]. International Journal of Fatigue，2002，24(9)：949-961.

[4]Wang Bo，Lu Hongbing，Gyuo-Ho Kim. A Damage Model for the Fatigue Life of Elastomeric Materials[J]. Mechanics of Materials，2002，34(8)：475-483.

[5] Saintier N，Cailletaud G，Piques R. Multiaxial Fatigue Life Prediction for a Natural Rubber[J]. International Journal of Fatigue，2006，28(5/6)：530-539.

[6] 徐 明. 橡膠類超彈性材料本構關系研究及有限元分析[D]. 北京：北京航空航天大學，2002.Xu Ming. The Constitutive Relations and Finite Element Analysis of Hyperelastic Rubber[D]. Beijing：Beijing University of Aeronautics and Astronautics，2002.

[7] 殷 聞，靳曉雄，仝 光. 兩種常用橡膠本構模型的有限元分析及仿真[J]. 上海電機學院學報，2010，13(4)：215-218. Yin Wen，Jin Xiaoxiong，Tong Guang. Finite Element Analysis of Rubber Constitutive Models and Simulation [J]. Journal of Shanghai Dianji University，2010，13(4) ：215-218.

[8] 上官文斌，呂振華. 汽車動力總成橡膠隔振器彈性特性的有限元分析[J]. 內燃機工程，2003，24(6)：50-55. Shangguan Wenbin，L Zhenhua. Finite Element Analysis of Elastic Characteristics of Rubber Isolator for Automotive Powertrain[J]. Chinese Internal Combustion Engine Engineering，2003，24(6)：50-55.

[9] 陳 蓮，周海亭. 計算橡膠隔振器靜態特性的數值分析方法[J]. 振動與沖擊，2005，24(3)：120-123. Chen Lian，Zhou Haiting. The Method of FEA on Static Characteristics of Rubber Isolator[J]. Journal of Vibration and Shock，2005，24(3)：120-123.

[10]李曉芳，楊曉翔. 橡膠材料的超彈性本構模型[J].彈性體，2005，15(1)：50-58. Li Xiaofang，Yang Xiaoxiang. Constitutive Models for Hyperelastic Material of Rubber[J]. Elastomer，2005，15 (1)： 50-58.

[11]Fazilay Laraba-Abbes，Patrick Ienny，Roland Piques.A New‘Tailor-Made’Methodology for the Mechanical Behavior Analysis of Rubber-Like Materials：Ⅱ. Application to the Hyperelastic Behavior Characterization of a Carbon-Black Filled Natural Rubber Vulcanizate[J]. Polymer，2003，44(3)：821-840.

[12]Boyce M C ，Arruda E M. Constitutive Models of Rubber Elasticity：a Review[J]. Rubber Chemistry and Technology， 20007，3(3)：504-52.

[13]A·N·詹特. 橡膠工程：如何設計橡膠配件[M]. 北京：化學工業出版社，2002：127-132. Gent A N. Rubber Engineering：How to Design Rubber Components[M]. Beijing：Chemical Industry Press，2002：127-132.

[15]Brackbill R B，Lesicutre G A，Smith E C, et al. Characterization and Modeling of the Low Strain Amplitude and Frequency Dependent Behavior of Elastomeric Damper Materials[J]. Journal of the American Helicopter Society, 2000：34-42.

[16]Horton J M. Stiffness of Rubber Bush Mountings Subjected to Radial Loading[J]. Rubber Chemistry and Technology, 2000，73(2)：253-264.

[17]卜繼玲，黃友劍. 軌道車輛橡膠彈性元件設計計算方法[M]. 北京：中國鐵道出版社，2010：53. Bu Jiling，Huang Youjian. Design and Calculation Method of Railway Vehicle Rubber Elastic Component[M]. Beijing：China Railway Publishing House，2010：53.

[18]中國船舶工業總公司第七研究院七零四研究所. GB/ T15168—94振動與沖擊隔振器性能測試方法[S]．北京：中國標準出版社，1994：1-12. Seven zero four of the Seventh Research Institute of Shipbuilding Industry Corporation of China. GB/ T15168—94 Vibration and Shock Isolators Performance Measurement Method[S]. Beijing：Standard Press of China 1994：1-12.

（責任編輯：申 劍）

Simulation Research on Dynamic Performance of Rubber Damping Brackets of Wind Turbine

Fang Jianhui1，Ding Zhiping1，Pu Jiling2，Huang Youjian2，Li Fei1，Bai Xiaopeng1
（1. School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Zhuzhou Time New Material Technology Co., Ltd., Zhuzhou Hunan 412007, China）

Based on three hyperelastic rubber material constitutive models of Mooney-Rivlin, Ogden 3 order and Van der Waals, and taking into consideration of influencing factors of load frequency, load amplitude and load mean value，the finite element models of rubber damping brackets of wind driven generator were established respectively and the dynamic properties of rubber damping brackets were made numerical simulation. Through rubber brackets dynamic bearing test, the effects of constitutive models of different rubber materials on simulation accuracy of rubber elastic parts were analyzed. The analysis of rubber damping bracket simulation and dynamic bearing test result error both indicated that Van der Waals model was suitable for compressing and shearing deformation load cases, Mooney-Rivlin model was for small or medium deformation load cases and Ogden 3 order model was for large deformation load cases. The appropriate rubber material constitutive model needs to be selected to improve the precision of FEA according to load cases.

rubber；finite element；constitutive model；dynamic stiffness；error

TQ332；U467.4+97

A

1673-9833(2014)02-0016-07

2013-12-25

湖南省教育廳重點科研基金資助項目（08A014），湖南省十二五機械工程重點學科基金資助項目（湘教發[2011] 76號）

方建輝（1985-），男，湖南岳陽人，湖南工業大學碩士生，主要研究方向為機械結構強度理論及應用，

E-mail：446997887 @qq.com

10.3969/j.issn.1673-9833.2014.02.004