振動壓路機模型仿真探討

張曉曦

（江蘇省交通科學研究院股份有限公司 南京 210017）

在工程質量和進度要求越來越嚴格的今天，振動壓路機一直受到廣大施工單位的青睞。隨著控制技術和振動壓實技術的日益提高，特別是微電子技術、計算機技術和自動化控制計算的不斷發展，振動壓路機還有不可限量的發展前景。為了更清楚地了解振動過程中加速度的改變對被壓材料壓實效果的影響，筆者結合試驗段實際工程，通過設置壓路機的初始參數，對振動壓路機進行模擬仿真［1］。

1 基于Matlab／Si mulink對振動壓路機控制系

統仿真

Si mulink是Matlab軟件的一個工具箱，它是結合了框圖界面和交互仿真能力的非線性動態性系統仿真工具，以Matlab的核心數學、圖形和語言為基礎。Si mulink Blockset是專門為特定領域設計的Si mulink功能塊的集合［2－3］。利用它對振動壓路機控制系統進行仿真具有重要意義。

（1）在仿真過程中，可以求解各種復雜的代數方程、偏微分方程及積分方程等。在某種程度上，仿真與理論和試驗相比，其對問題的認識更為細致、深刻，可以清晰地了解問題本質，而且可重復地、隨時地、連續動態地觀察事物的發展狀況。

（2）可以清晰、直觀地解釋一些現象，易于分析理解，可以顯示發生在結構內部的物理現象。

（3）仿真完善了試驗，可以對試驗方案的正確制定、試驗中的合理測點布置、儀表量程選擇等提供更加可信的理論依據。

（4）和試驗不同，仿真軟件可以復制拷貝，重復利用，可以進行適當改變，以滿足不同試驗條件的需求

。

2 模型仿真

2.1 理論分析

選擇典型機械輪胎驅動振動壓路機為對象，寫出并分析振動系統運動方程，以兩自由度的數學模型為例，見圖1。首先假設對模型的有關參數和條件。

圖1 振動壓路機數學模型

（1）土是彈性體，具有一定剛度，其值為K2，阻尼為線性阻尼，其值為C2。

（2）振動壓路機上車質量為m1，瞬時位移為x1，下車質量為m2，瞬時位移為x2，且上下車簡化具有一定質量的集中質量塊。

（3）振動碾壓過程中，任意時刻振動輪始終保持與碾壓面緊密接觸。數學模型的運動方程為

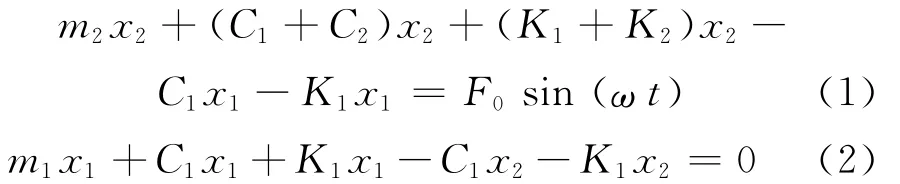
式中：m1為上車的質量；m2為下車質量（振動質量）；K1為減振器剛度；K2為土的剛度；C1為減振器阻尼；C2為土的阻尼；F0為激振力幅值；x1為上車瞬時位移（瞬時振幅）；x2為下車瞬時位移（瞬時振幅）；ω為工作頻率（角頻率）；Fs為下車對路面的作用力。

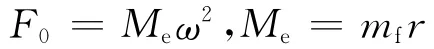
式中：Me為偏心塊靜偏心力矩；mf為偏心力；r為偏心距。

振動系統與激振力系統有相同的頻率ω做強迫振動。式（1），（2）微分方程的解為：

式中：A1＝k1－m1ω2·B1＝C1ω；A2＝k1·B1＝C1ω；C＝m2m1ω4－m2K1ω2－C1C2ω2＋K1K2－m1K1ω2；D ＝ K2C1ω ＋ K1C2ω2－ m2C1ω3－m1C2ω3－m1C1ω3

振動輪在簡諧力激振力作用下，垂直加速度幅值為

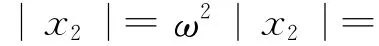
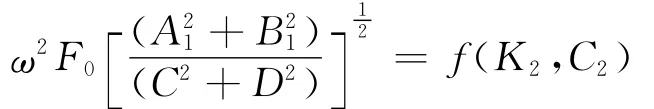
2.2 仿真模型與方法

首先，在Si mulink Library Browser各模塊庫中選取合適的模塊；其次，根據動力學方程所描述的關系構建起系統的仿真框圖，見圖2。最后在各模塊參數修改框中輸入初值，保存、運行，進行仿真［4－5］，見圖3、圖4。

圖2 系統仿真圖

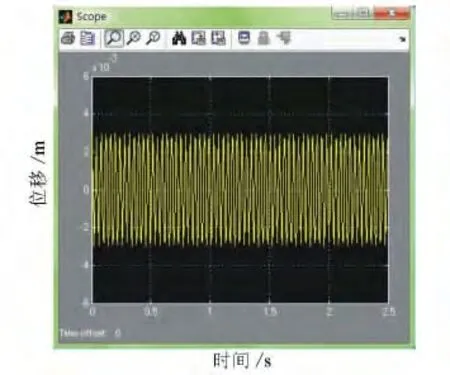
圖3 振動輪位移響應

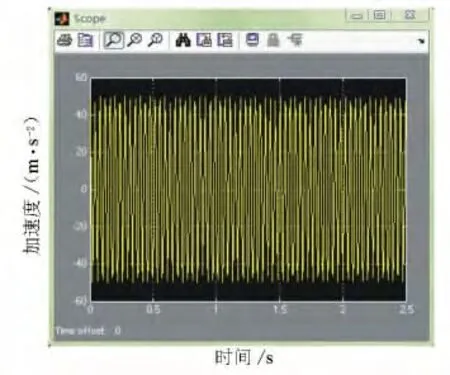
圖4 振動輪加速度響應

由圖3可見，起振瞬間有較大的位移，此后振動頻率增大且趨于穩定，其原因是路堤填石料受迫振動逐漸密實。由圖4可見，振動輪是由多同頻率的簡諧運動疊加而成，而不是一種頻率的簡諧運動。振動壓路機工作時，由于路面的情況復雜多變，其固有頻率也不盡相同，這樣單一頻率激振就顯得不足。多頻率疊加的復雜激振，使得填石料更方便處于高頻狀態，對填石料的壓實效果更好。

2.3 仿真結果分析

依據工程實際和相關參考文獻，仿真時基本參數確定為m1＝3 000 kg，m2＝7 000 kg，F0＝4.3×105N，ω＝2πf，f＝30 Hz，K1＝1.6×106N／m，K2＝1.7×107N／m，C1＝5.25×104Ns／m，C2＝7.0×104Ns／m，ω＝2 300 r／min。

從理論分析了解到，振動加速度的變化與填石料的阻尼、剛度系數等因素有關。為使得仿真更真實，就要考慮這些因素的改變對仿真結果的影響。

當其他參數保持不變，填石料剛度系數由K2變為2 K2時，仿真時域圖變化見圖5。

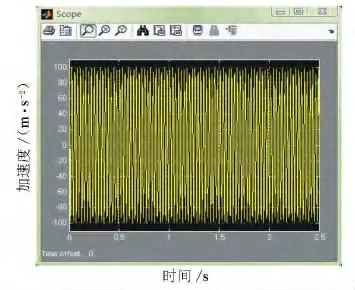
圖5 2 K 2情況下振動輪加速度響應

結合圖4和圖5可見，當填石料剛度為2 K2時，振動加速度的變化率增大，同時加速度幅值也增大，得到的振動輪的垂直加速度與填石料的剛度正相關。僅剛度變化時引起的仿真結果見圖6。

圖6 振動加速度隨剛度K 2的變化

由圖6可見，隨著剛度系數的增大，振動加速度也在增大。這表明隨著壓實度的增大，填石料剛度增大，振動加速度也增大，兩者正相關。

當其他參數保持不變，填石料的阻尼由C2變為2C2時，仿真時域圖變化見圖7。

結合圖3和圖7可見，阻尼為2C2時，振動加速度的變化頻率增大，幅值變小，表明加速度與壓實度也是相關的。這一結論與理論分析結果一致。僅阻尼變化時引起的仿真結果見圖8。

由圖8可見，隨著阻尼的增大，振動加速度隨之減小，兩者負相關。

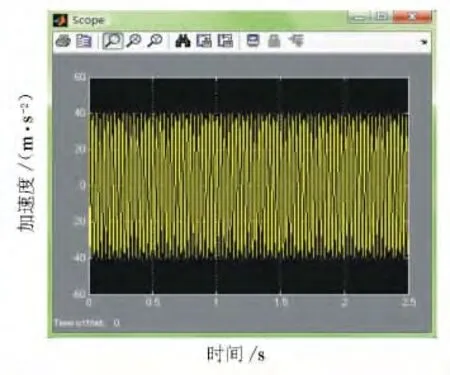
圖7 2C2情況下振動輪加速度響應

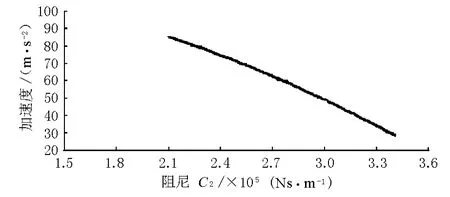
圖8 振動加速度隨陰尼C 2的變化

由以上系統模型仿真可以得到：振動壓路機的垂直加速度與填石料的阻尼、剛度密切相關。振動輪垂直加速度與路面材料相互作用，使被壓填石料的壓實密度增大。所以，選取壓路機振動輪的加速度間接反映被壓路面的壓實狀況是可行的。

3 信號的采集與分析

在壓實過程中，要對壓實狀態進行動態實時監控，以便了解壓實效果的狀態變化，這一變化就是一種信息。信息本身不能進行傳輸和交換，只能通過信號途徑才可實現這種傳遞和交換，信號是通過測試獲得的，其最終目的就是獲取信息。測試、信號、信息之間的關系見圖9。

圖9 信息與信號及測試的關系

由于振動壓路機對路堤的作用，其狀態會隨時發生變化，這種變化又可以反饋給壓路機，壓路機對該反饋作用的信息（動態響應）就是需要獲得的信息。該信息是通過測量系統進行采集、存儲，最后再傳遞給分析系統進行合理的分析判斷，并發出針對這種反饋信息的指令，目的是為了對壓路機及路基進行合理的控制提供可靠的依據，見圖10。

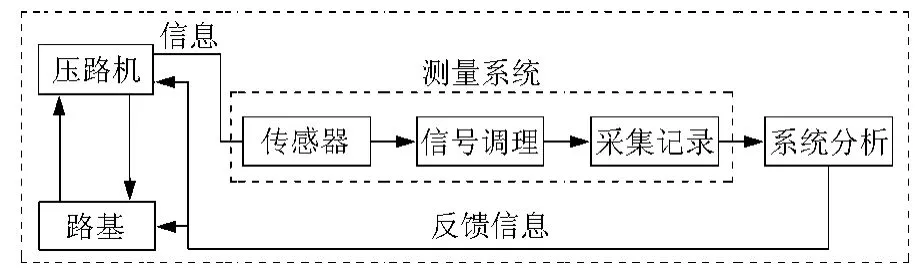
圖10 壓實過程信息的傳遞與獲取

經過振動信號分析、信號處理（信號濾波、噪聲分析、信號變換算法），最終反映信號。通過Matlab編程，對采集并經過處理的振動加速度信號進行Fourier變換，結果見圖11。圖11中出現了振動加速度幅值基波頻率和多次諧波頻率。圖中50 Hz對應的幅值為主頻對應的幅值，120 Hz對應的幅值為二次諧波對應的幅值。通過分析比較，取出基波和二次諧波成份，將其比值（CMV）作為路堤連續壓實質量控制的指標。

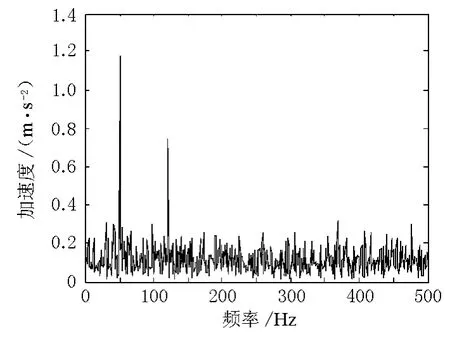
圖11 振動加速度信號頻譜

4 現場試驗

根據仿真試驗理論，選取某項目進行現場試驗。本試驗段為某單線電氣化I級干線標準鐵路，設計時速為120 k m／h。填石料最大粒徑10 c m，不均勻系數10～30，粗顆粒含量大于70%，攤鋪厚度45 c m的填石料，在自重19.8 t，強振時振動力43 t、弱振時振動力26 t、剛度3.1×107N／m、阻尼2.2×105Ns／m作用下，在相同條件下可以達到較好的壓實效果；CMV取值62.2可以作為參考值。

5 結論

（1）計算機仿真與試驗研究、理論分析相互依存，成為科學技術探索必不可少的手段。

（2）得到影響加速度因素（土體的剛度和阻尼），改變影響因素建立模型進行振動仿真，證實了壓實度與振動輪垂直加速度具有相關性，且是正相關的。而振動加速度與土體剛度是正相關的，與阻尼是負相關的。

（3）對壓實過程進行動態監測和控制時，壓實狀態的變化是一種信息。振動輪的加速度信號夾著某些高頻噪聲的正弦周期信號，需要對振動信號進行處理。

（4）復雜的動態信號中某些干擾成分必須使用濾波器進行濾波。快速Fourier變換（FFT）是離散Fourier的快速算法，使得運算更為簡化，應用更為廣泛。

（5）對采集并經過處理的振動加速度信號進行Fourier變換，然后取出基波成分和二次諧波成分，兩者比值稱為壓實度值（Compaction Meter Val ue／CMV），以此來表征壓實程度。

［1］ 楊 璐，馮占強.智能壓實技術發展概況［J］.工程機械，2011（1）：50-54.

［2］ 金 鑫.MATLAB在土工試驗數據處理中的應用［J］.巖土工程學報，2004，26（2）：272-275.

［3］ 徐 瑞，黃兆東.MATLAB 2007科學技術與工程分析［M］.北京：科學出版社，2008.

［4］ 楊 鈺.用快速傅里葉變換計算連續信號的頻譜［J］.湖南科技學院學報，2005，26（11）：192-193.

［5］ 秦四成.振動壓路機［M］.北京：人民交通出版社，1979.