腦卒中患者血清CHIL1、AnnexinA1與頸動脈粥樣硬化斑塊的關系及洛伐他汀干預效果
李永軍,杜明
(秦皇島市第四醫院檢驗科,河北 秦皇島 066000)
腦卒中患者血清CHIL1、AnnexinA1與頸動脈粥樣硬化斑塊的關系及洛伐他汀干預效果
李永軍,杜明
(秦皇島市第四醫院檢驗科,河北 秦皇島 066000)
目的 探討腦卒中患者血清幾丁酶樣蛋白1(CHIL1)、膜聯蛋白A1(AnnexinA1)與頸動脈粥樣硬化斑塊的關系及洛伐他汀干預效果。方法選取2014年6月至2015年6月本院綜合內科收治的168例首發腦卒中患者(腦卒中組),另選取160例身體健康體檢者為對照組,應用頸動脈彩色多普勒超聲檢查兩組頸動脈內-中膜厚度(IMT),應用全自動化生化分析儀測定兩組甘油三脂(TG)、總膽固醇(TC)、低密度蛋白(LDL-C)、高密度蛋白(HDL-C)水平,應用酶聯免疫法測定兩組血清CHI3L1、AnnexinA1水平,膠體金法測定兩組C反應蛋白(CRP)。應用Pearson單因素分析腦卒中患者IMT與血脂水平及血清CHIL1、AnnexinA1水平的關系。應用Logistic多因素分析腦卒中發生危險因素,對腦卒中患者給予洛伐他汀干預,20 mg/次,1次/d,共干預6個月,觀察其干預效果。結果腦卒中組患者的IMT、血清TG、TC、LDL-C、CHIL1及CRP水平均高于對照組,而HDL-C、AnnexinA1水平低于對照組,差異均有統計學意義(P<0.05);經Pearson相關性分析顯示,IMT與TG、TC、LDL-C、CHIL1、呈正相關(P<0.05),而與AnnexinA1 HDL-C呈負相關(P<0.05);經Logistic多因素分析顯示,IMT、LDL-C、CHIL1、是腦卒中發生的獨立危險因素(P<0.05),而AnnexinA1 HDL-C是腦卒中發生的保護因素(P<0.05)。經洛伐他汀干預3個月、6個月后腦卒中患者IMT、血清TG、TC、LDL-C、CHIL1及CRP水平較治療前顯著下降,血清AnnexinA1 HDL-C水平較治療前升高,差異均有統計學意義(P<0.05)。結論IMT、LDL-C、CHIL1是腦卒中發生的獨立危險因素,而HDL-C是腦卒中發生的保護因素。洛伐他汀可通過抑制IMT形成,降低血脂及CHIL1、CRP水平,預防腦卒中復發。
腦卒中;幾丁酶樣蛋白1;膜聯蛋白A1;頸動脈粥樣硬化斑塊;洛伐他汀
頸動脈粥樣硬化斑塊形成、破潰、出血等病理過程可激活機體凝血系統,促使血栓形成,引起腦血管栓塞是導致腦血管疾病發生的重要機制之一[1]。目前大量研究指出,炎癥在動脈粥樣斑塊形成、發展、破潰及斑塊出血過程中起到重要的作用[2-3]。血清C反應蛋白(C-reactive protein,CRP)是機體炎癥反應重要標記物,同時也是腦卒中發生的危險因素[4]。幾丁酶樣蛋白1(chitinase-like protein,CHIL1)主要由血管平滑肌細胞、上皮細胞、脂肪細胞、軟骨細胞、巨噬細胞等分泌的細胞,在機體急、慢性炎癥反應中起到重要的作用,同時可影響斑塊穩定性,導致斑塊破潰、出血[5]。膜聯蛋白A1(AnnexinA1)是機體重要炎癥調控細胞,在抑制炎癥代謝產物生成、內皮細胞與中性粒細胞黏附過程中起到重要的作用[6]。洛伐他汀能有效抑制機體炎癥反應、抑制血小板聚集、抑制粥樣硬化區血栓形成,抑制平滑肌增生,能有效穩定及縮小頸動脈硬化斑塊[7]。本研究將分析腦卒中患者血清CHIL1、AnnexinA1、CRP與頸動脈粥樣硬化斑塊的關系及應用洛伐他汀干預的效果,旨在為腦出血患者臨床預防及治療提供指導。
1 資料與方法
1.1 一般資料 選取2014年6月至2015年6月本院綜合內科收治的168例首發腦卒中患者。納入標準:①患者均符合全國第4次腦血管疾病會議中對腦卒中的診斷標準;②均經頭部MRI或CT確診;③均簽署知情同意書。排除標準:①肝腎功能不全、惡性腫瘤、急性顱腦損傷、急性感染、血液系統性疾病、有出血史、消化道潰瘍史患者;②入組前已經進行過抗凝、抗血栓治療者。168例患者中男性82例,女性86例;年齡45~75歲,平均(56.3±3.2)歲;患者發病至送院時間為0.5~12 h,平均(5.5±0.7)h;合并高血壓82例,合并高血脂42例,合并糖尿病32例。另選取160例身體健康體檢者為對照組,患者經影像學檢查、實驗室檢查排除相關病變,其中男性84例,女性76例;年齡48~80歲,平均(57.2±3.8)歲。兩組受檢者的性別、年齡比較差異均無統計學意義(P>0.05),具有可比性。
1.2 方法
1.2.1 頸動脈內-中膜厚度測定 分別于腦卒中患者入院當天及對照組體檢當天采用美國飛利浦D5型高頻彩色多普勒超聲診斷儀,檢查時受試者取頭后仰臥位,頭部偏向對側45°,探頭頻率為10~15 MHz,掃描范圍為雙側頸總動脈分叉處,測定雙側頸總動脈IMT。IMT為頸總動脈中膜與后壁內膜上緣厚度之和。
1.2.2 血液樣本制備 分別于腦卒中患者入院第2天及對照組體檢當天各抽取靜脈血6 mL,以3 000 r/min速度,離心半徑為5 cm離心處理樣本,并留取上清液。各自將上清液分裝于兩支試管中,分別為A、B試管,其中A試管用于測定血脂水平,B試管用于測定血清CHIL1、AnnexinA1、CRP水平。
1.2.3 血脂水平測定 應用HITACHI7080全自動生化分析儀測定兩組血清TG、TC、LDL-C、HDL-C水平。
1.2.4 血清CHIL1、AnnexinA1、CRP水平 應用酶聯法測定兩組血清CHIL1、AnnexinA1水平,CHIL1試劑盒購于北京方程生物科技有限公司,AnnexinA1試劑盒購于上海武昊經貿有限公司,CRP試劑盒購于上海博研生物科技有限公司,操作過程嚴格按照試劑盒說明書進行操作。
1.2.5 洛伐他汀干預 對腦卒中患者行神經內科常規治療,如抗凝、抗血小板、積極控制血壓、活血化瘀,同時給予患者低脂飲食,加強患者體育運動,減輕患者體重,在此基礎上給予患者洛伐他汀(廠家:黑龍江肇東華富藥業有限責任公司;生產批號:201405823)干預,20 mg/次,1次/d,共治療6個月,期間對患者進行隨訪,所有患者均獲得隨訪。分別于治療3個月、治療6個月測定各組IMT、血清TG、TC、LDL-C、HDL-C、CHI3L1、AnnexinA1及CRP水平。
1.3 統計學方法 應用SPSS19.0統計軟件進行數據分析,計量資料以均數±標準差(±s)表示,多組比較采用重復測量方差分析,應用Pearson相關性分析腦卒中患者IMT與血脂水平及血清CHI3L1、AnnexinA1水平的關系,應用多因素Logistic回歸分析腦卒中發生危險因素,以P<0.05為差異有統計學意義。
2 結 果
2.1 兩組受檢者的IMT、血脂、CHIL1、AnnexinA1及CRP水平比較 腦卒中組患者的IMT、血清TG、TC、LDL-C、CHIL1及CRP水平均高于對照組,而HDL-C、AnnexinA1水平低于對照組,差異均有統計學意義(P<0.05),見表1。
表1 兩組受檢者的IMT、血脂、CHIL1、AnnexinA1及CRP水平比較(±s)

表1 兩組受檢者的IMT、血脂、CHIL1、AnnexinA1及CRP水平比較(±s)
組別腦卒中組對照組t值P值例數168 160 IMT(mm) 2.12±0.42 0.15±0.08 58.327<0.01 TG(mmol/L) 5.23±0.85 2.02±0.21 46.435<0.01 TC(mmol/L) 3.28±0.86 1.85±0.32 19.768<0.01 LDL-C(mmol/L) 3.89±0.56 1.79±0.22 44.288<0.01 HDL-C(mmol/L) 1.52±0.36 3.52±0.45 44.551<0.01 CHIL1(μg/L) 121.02±7.98 32.02±5.26 118.64<0.01 AnnexinA1(μg/L) 1.25±0.25 5.48±0.14 58.038<0.01 CRP(mg/L) 12.85±3.85 2.63±0.72 33.030<0.01
2.2 腦卒中患者IMT與血脂、CHIL1、AnnexinA1及CRP的關系 經Pearson相關性分析顯示,IMT與TG、TC、LDL-C、CHIL1、CRP呈正相關(P<0.05),而與AnnexinA1、HDL-C呈負相關(P<0.05),見表2。

表2 腦卒中患者IMT與血脂、CHIL1、AnnexinA1及CRP的關系
2.3 影響腦卒中發生的多因素Logistic回歸分析 以腦卒中發生為因變量,以影響腦卒中發生的相關因素為自變量行多因素Logistic回歸分析,結果顯示,IMT、LDL-C、CHIL1是腦卒中發生的獨立危險因素(P<0.05),而AnnexinA1、HDL-C是腦卒中發生的保護因素(P<0.05),見表3。
2.4 腦卒中患者經洛伐他汀干預前后相關指標的變化 經洛伐他汀干預3個月、6個月后,腦卒中患者IMT、血清TG、TC、LDL-C、CHIL1、CRP水平較治療前明顯下降,血清HDL-C、AnnexinA1水平較治療前明顯升高,差異均有統計學意義(P<0.05),見表4。
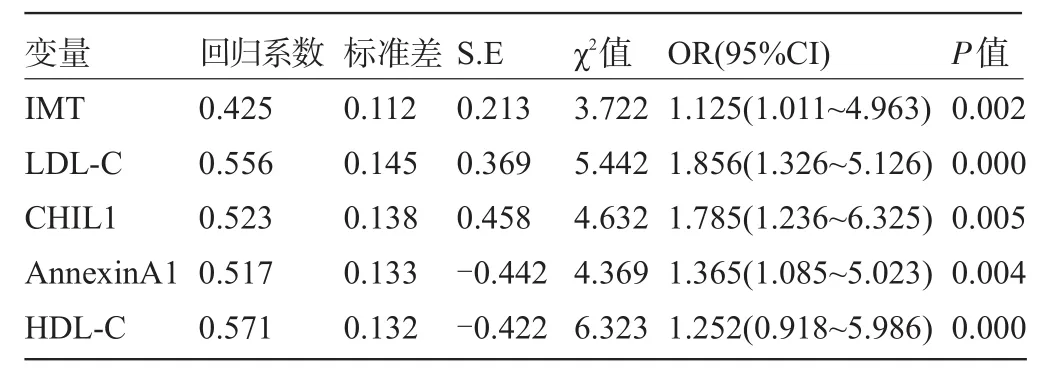
表3 影響腦卒中發生的Logistic多因素分析
表4 腦卒中患者經洛伐他汀干預前后相關指標的變化(±s)

表4 腦卒中患者經洛伐他汀干預前后相關指標的變化(±s)
注:與干預3個月比較,aP<0.05;與干預6個月比較,bP<0.05。
時間干預前干預3個月干預6個月F值P值例數168 168 168 IMT(mm) 2.12±0.42 1.02±0.28a0.85±0.11ab897.53<0.01 TG(mmol/L) 5.23±0.85 3.28±1.02a2.12±0.86ab497.46<0.01 TC(mmol/L) 3.28±0.86 2.89±1.05a1.45±0.39ab234.81<0.01 LDL-C(mmol/L) 3.89±0.56 3.02±1.10a2.12±0.528ab220.06<0.01 HDL-C(mmol/L) 0.89±0.12 1.52±0.28a1.98±0.32ab221.25<0.01 CHIL1(μg/L) 121.02±7.98 85.26±8.36a52.88±5.78ab350.65<0.01 AnnexinA1(μg/L) 1.25±0.25 3.02±0.68a5.12±0.45ab562.66<0.01 CRP(mg/L) 12.85±3.85 8.25±3.02 4.32±1.22 361.24<0.01
3 討 論
近年普遍認為慢性炎癥反應與頸動脈斑塊的形成有密切的關系[8],頸動脈粥樣硬化斑塊形成及發展過程均有炎癥因素參與,且存在炎癥級聯免疫反應。炎癥因素尤其是內皮細胞與單核細胞粘附、遷移是頸動脈斑塊硬化形成及進展的關鍵因素。
AnnexinA1屬于脂蛋白相關磷脂酶A2(LP-PLA2)家族中的一員,可抑制LP-PLA2生成,從而起到抗炎作用。此外,AnnexinA1抗炎作用還體現在它可抑制單核細胞及中性粒細胞遷移及聚集,并可激活甲酰基肽受體(FPR)、L-選擇素(L-Selectin)[9]。近年,Makani等[10]研究指出,AnnexinA1可激活中性粒細胞FPR而抑制對內皮細胞的損傷作用。Hughes等[11]認為,AnnexinA1可與血管細胞粘附分子-1競爭性結合整合素,抑制血管內皮細胞與單核細胞粘附,從而參與早期炎癥反應調節。此外,AnnexinA1也可抑制相關參與炎癥反應的酶表達,如環氧化酶-2、一氧化氮合酶等,從而發揮抗炎作用。本研究結果顯示,腦卒中患者血清AnnexinA1水平顯著低于正常對照組,且與IMT呈負相關,經Logistic多因素分析可知,AnnexinA1是腦卒中發生的保護因素,表明AnnexinA1水平下降與機體炎癥反應發生有密切的關系。CHIL1是新近發現的炎癥因子,可在血管平滑肌細胞、脂肪細胞、上皮細胞、巨噬細胞等多種細胞中表達,且與冠狀動脈狹窄病變程度有密切的關系。Hinsinger等[12]應用免疫組織化學法測定腦卒中患者頸動脈硬化斑塊中CHIL1表達水平,結果表明,與正常人群相比,腦卒中患者斑塊中CHIL1陽性表達強度顯著高于正常人群,且可導致斑塊不穩定,并促進斑塊破裂出血。CRP是心腦血管疾病發生的獨立危險因素,可促使單核細胞聚集、促進單核細胞組織因子釋放,并激活補體系統,介導內皮細胞損傷,可促進巨噬細胞進入血管內皮,促進血管炎癥反應及血栓形成,并介導粘附分子釋放[13]。本研究中腦卒中患者血清CHIL1、CRP水平顯著高于正常對照組,且與頸動脈斑塊形成有密切的關系,是腦卒中發生的獨立危險因素,表明血清CHIL1、CRP異常表達可增加腦卒中發生的風險。
多項研究指出,他汀類藥物在降低血脂及心血管事件中有良好的預防作用[14-15]。本研究結果顯示,對腦卒中患者洛伐他汀干預6個月能明顯降低患者TG、TC、LDL-C水平,抑制IMT形成。相關資料顯示,IMT形成與LDL-C有關,且與HDL-C呈負相關[16],表明血脂水平在IMT形成及發展過程起到重要的作用。其可能機制為氧化低密度脂蛋白是動脈粥樣硬化的危險因子,可促進血管平滑肌增殖及分化,而洛伐他汀可促進低密度脂蛋白降解,阻止LDL-C氧化分解,抑制血管平滑肌增殖及分化,因此能有效改善腦卒中患者頸動脈粥樣斑塊硬化。此外,本研究結果顯示,洛伐他汀能有效抑制CHIL1、CRP生成,促進AnnexinA1產生及分泌,從而起到抗炎作用。
綜上所述,IMT、LDL-C、CHIL1是腦卒中發生的獨立危險因素,而AnnexinA1 HDL-C是腦卒中發生的保護因素。洛伐他汀可通過抑制IMT形成,降低血脂及CHIL1、CRP水平,預防腦卒中復發。
[1]申麗紅,梁小樂,高旭光,等.急性腦梗死患者微栓子與頸動脈粥樣硬化斑塊的相關性研究[J].中華老年心腦血管病雜志,2014,16 (3):237-239.
[2]王燕嬉.急性腦梗死患者血清內脂素、高敏C反應蛋白及血栓前體蛋白與頸動脈粥樣硬化斑塊的相關性[J].中國老年學雜志,2016, 36(12):2908-2909.
[3]李鳳,朱余友,楊孫鳳,等.血清五聚素3、超敏C反應蛋白、脂蛋白相關磷脂酶A2水平以及微栓子信號與大動脈粥樣硬化型急性腦梗死患者頸動脈粥樣硬化斑塊穩定性的相關研究[J].臨床神經病學雜志,2016,29(2):95-100.
[4]朱衛香,劉彥敏,韓亞軍,等.缺血性腦卒中患者血清基質金屬蛋白酶-9、超敏C反應蛋白水平與頸動脈粥樣硬化的相關性[J].疑難病雜志,2014,2(11):1111-1113.
[5]李祥波,吳成穩,王耀磊,等.人頸動脈粥樣硬化斑塊中幾丁質酶樣3蛋白1及基質金屬蛋白酶-9的表達[J].中華實驗外科雜志,2015, 32(12):3016-3019.
[6]王春梅,王成鋼,聶紹平,等.血清膜聯蛋白A1與冠狀動脈狹窄程度的相關性研究[J].中國全科醫學,2015,18(36):4408-4411.
[7]孫麗靜,白麗華,趙惠,等.不同劑量洛伐他汀治療冠心病伴高脂血癥的臨床觀察[J].臨床合理用藥雜志,2014,7(4):31-32.
[8]Liu JH,Feng D,Zhang YF,et al.Chloral hydrate preconditioning protects against ischemic stroke via upregulating annexin A1[J].CNS Neurosci Ther,2015,21(9):718-726.
[9]Zhao B,Wang J,Liu L,et al.Annexin A1 translocates to nucleus and promotes the expression of pro-inflammatory cytokines in a PKC-dependent manner after OGD/R[J].Sci Rep,201,18(6):27028-27030.
[10]Makani V,Sultana R,Sie KS,et al.Annexin A1 complex mediates oxytocin vesicle transport[J].J Neuroendocrinol,2013,25(12): 1241-1254.
[11]Hughes EL,Cover PO,Buckingham JC,et al.Role and interactions of annexin A1 and oestrogens in the manifestation of sexual dimorphisms in cerebral and systemic inflammation[J].Br J Pharmacol, 2013,169(3):539-553.
[12]Hinsinger G,Galéotti N,Nabholz N,et al.Chitinase 3-like proteins as diagnostic and prognostic biomarkers of multiple sclerosis[J]. Mult Scler,2015,21(10):1251-1261.
[13]黃曉蕓,徐安定,梅志忠,等.炎癥因子與急性動脈粥樣硬化性腦梗死及其預后的關系[J].廣東醫學,2015,2(19):2994-2997.
[14]侯衛靜,王慶勝,張晶.他汀類藥物對低密度脂蛋白膽固醇正常的動脈粥樣硬化人群的干預作用[J].醫學綜述,2016,22(6): 1141-1144.
[15]賴誠民,陳勇.他汀類藥物對老年冠心病患者動脈粥樣硬化程度的影響[J].中國老年學雜志,2015,2(16):4507-4509.
[16]徐剛,袁濤,韓增雷,等.冠心病患者頸動脈IMT及斑塊總積分與冠脈Gensini積分的關系[J].中國臨床研究,2013,26(11):1153-1154.
Relationship between serum CHIL1,annexin A1 and carotid atherosclerotic plaques in patients with stroke and the interventional effect of lovastatin.
LI Yong-jun,DU Ming.Department of Clinical Laboratory,the Fourth Hospital of Qinhuangdao,Qinhuangdao 066300,Hebei,CHINA
Objective To investigate the relationship between serum chitinase like protein 1(CHIL1),annexinA1 and carotid artery atherosclerotic plaques in patients with stroke and the interventional effect of lovastatin.MethodsA total of 168 patients of stroke,who admitted to Department of General Cardiology of our hospital from June 2014 to June 2015,were selected as the stroke group,and 160 healthy volunteers were selected as the control group during the same time.The carotid intima-media thickness(IMT)of the two groups was measured by ultrasound with carotid color Doppler.The levels of triglyceride(TG),total cholesterol(TC),low-density protein(LDL-C),and high density protein (HDL-C)of the two groups were identified with fully automated biochemistry analyzer.The levels of CHIL1,ANXA1 were measured with enzyme-linked immunosorbent assay(ELISA).The levels of C-reactive protein(CRP)of the twogroups were evaluated with the colloidal gold method.The relationships between IMT and the levels of serum lipid, CHIL1,ANXA1 in patients with stroke were analyzed by Pearson single factor.Logistic multivariate analysis was used to analyze the risk factors of stroke.Lovastatin was given to patients with stroke at the dose of 20 mg once a day for 6 months,and the intervention effect was observed.ResultsThe levels of IMT,serum TG,TC,LDL-C,CHI3L1 and CRP of the stroke group were significantly higher than those of the control group(P<0.05),while the levels of annexin A1,HDL-C of the stroke group were significantly lower than those of the control group(P<0.05).Pearson's single factor analysis showed that IMT were positively correlated with TG,TC,LDL-C,CHIL1(P<0.05)and negatively correlated with annexin A1,HDL-C(P<0.05).Logistic multivariate analysis showed that IMT,LDL-C,CHIL1 were the independent risk factors of stroke,while annexin A1,HDL-C was the protective factors of stroke(P<0.05).After three and six months of lovastatin intervention,the levels of IMT,serum TG,TC,LDL-C,CHIL1,and CRP in patients with stroke were significantly lower than before the lovastatin intervention,while the level of annexin A1,HDL-C was significantly higher than before the lovastatin intervention(P<0.05).ConclusionIMT,LDL-C,CHIL1 are the independent risk factors of stroke,while annexin A1,HDL-C are the protective factor of stroke.Lovastatin can prevent the recurrence of stroke by inhibiting the formation of IMT and reducing the levels of serum lipids and CHIL1,and CRP.
Stroke;Chitinase like protein 1(CHIL1);AnnexinA1;Carotid atherosclerotic plaque;Lovastatin
R743.3
A
1003-6350(2017)04-0540-04
10.3969/j.issn.1003-6350.2017.04.007
2016-09-06)
李永軍。E-mail:liyongjunqh@163.com

