行走激勵下樓蓋振動加速度反應譜研究

陳 雋，葉 艇，彭怡欣，3

（1.土木工程防災國家重點實驗室，上海 200092；2.同濟大學，上海 200092；3.香港理工大學，香港，九龍紅磡）

行走激勵下樓蓋振動加速度反應譜研究

陳 雋1，2，葉 艇2，彭怡欣2，3

（1.土木工程防災國家重點實驗室，上海 200092；2.同濟大學，上海 200092；3.香港理工大學，香港，九龍紅磡）

利用320條實測中國人步行荷載曲線，由振型分解法計算了步行荷載作用下大跨混凝土樓蓋豎向振動的10 s加速度均方根反應譜曲線。基于樓蓋頻率與振動幅值雙控原則，對計算反應譜進行了擬合簡化，提出了3～20 Hz頻率范圍的設計用樓蓋均方根加速度響應計算表達式。進一步討論了高階振型、邊界條件、計算跨度、行走步幅和阻尼比等要素對反應譜的影響，并給出了對應的修正方法。最后通過與已建大跨樓蓋步行激勵下實測加速度響應的比較，驗證了所建議的反應譜計算方法的合理性。

步行荷載；大跨度混凝土樓蓋；加速度均方根反應譜；參數分析

隨著跨度的不斷增大、新型輕質建筑材料的應用，以及無隔墻布置方式的流行，大跨混凝土樓蓋在人致激勵作用下的振動舒適度問題在工程設計中日益突出。設計階段主要通過限制樓蓋頻率下限值或限制結構加速度響應上限值兩種方法來處理樓蓋振動舒適度問題，后一種方法更為合理。因此，在結構布置方案變化頻繁的初步設計階段，如何快速準確地計算人致激勵下的樓蓋響應，就顯得非常的關鍵，而采用反應譜方法是主要途徑之一。

宋志剛等［1］利用國外不同學者實驗所獲得的步頻為2.2、1.6和1.9 Hz的單足落步荷載曲線，計算了跨度為6 m的簡支梁結構的加速度峰值反應譜，對此3條反應譜擬合得到針對不同阻尼比的計算反應譜，并討論了邊界條件，高階振型和跨度對反應譜的影響。聶建國等［2］基于Willford等［3］提出的步行荷載模型逆向構建了步頻為1.6～2.4 Hz的單足落步曲線，并計算了跨度為7.5～150 m的單跨簡支人行橋的加速度均方根反應譜，討論了步頻、跨度、阻尼比和邊界條件等參數的影響。按照與文獻［2］相同的方法，陳宇等［4］建立了適用于二～四跨連續人行橋的加速度均方根反應譜，考慮了跨度比對響應的影響。韓小雷等［5］通過引入對行人行走模式、開始時間、行走路線、體重分布等計算參數分布特性的假定，通過隨機生成步行荷載計算了人群行走下樓蓋的響應并擬合了反應譜，適用樓蓋頻率范圍4～14 Hz，文中未明確單人步行荷載模型的選取方式。Ungar等［6］基于文獻［7－9］中實測2.08、1.67、1.25 Hz步頻的單足落步曲線，計算并擬合了單自由度體系加速度、速度峰值及均方根值反應譜。該研究針對高頻樓板，譜的適用范圍為5～20 Hz。

前述反應譜研究工作中大都選用國外步行荷載數據或數學模型，而大量醫學研究已表明中國成年人的足底壓力分布、步行荷載特性以及行走特點與西方人差異較大［10－12］。另一方面，僅采用單足落步曲線也忽略了左右腳差異所引起的次諧波效應，造成荷載譜特性不完整。此外，研究所建議反應譜方法大都未與工程實測響應進行對比驗證。針對上述問題，本文根據實測中國人步行荷載曲線，計算了大跨度樓蓋的加速度均方根反應譜，基于頻率和振幅雙控原則，提出了3～20 Hz頻率范圍的設計用反應譜公式與參數修正方法，并與實測樓蓋響應進行了比較。

1 標準加速度均方根值反應譜

1.1 步行荷載曲線的選取

利用三維動作捕捉技術結合固定測力板，課題組已完成了100多人次多種步頻下步行荷載動力特性試驗。圖1為實驗情形，圖2為某男性測試者（身高1.79 m，體重72 kg，固定步頻2.0 Hz）左、右腳所測單足落步曲線（虛線）和兩個單步的合力（實線）。

圖1 采用三維動作捕捉技術的步行荷載特性實驗情況Fig.1Walking load experiment using 3D motion capture and fixed force plates

圖2 典型落步曲線實驗記錄Fig.2 Typical footfall curvesmeasured in the test

動作捕捉系統可記錄試驗者步行時足部的軌跡，以及每足著地和離地的準確時刻。據此可將實測復步步行荷載曲線（即圖2中實線）進行了拓展，得到連續的步行荷載曲線［14－15］。本文最終采用了來自60位測試者的總共320條步行荷載曲線，其頻率分布覆蓋了常見的1.5～2.5 Hz步頻范圍。與以往研究大多采用單足落步荷載曲線（且多為數值模型）不同，本研究采用的是由實測的復步步行荷載曲線，可更準確體現次諧波效應的影響［14－15］。有關步行荷載實驗的更詳細的描述見文獻［13］。

1.2 標準激勵系統均方根加速度反應譜

對于四邊簡支的矩形薄板，考慮沿板中線行走的最不利方式，利用振型分解方法可得板響應計算方程如下［1，15］：

式中：Yjk、ωjk、ξjk、Mjk、arefjk分別是樓板第（j，k）階振型的位移、頻率、阻尼比、振型質量和參考加速度；j，k分別是行走方向和垂直行走方向板振型編號；G是行人體重；Fj（t）是行走方向第j振型的標準激勵曲線，由振型廣義力（實測步行荷載曲線乘振型）除體重G得到［1，16］。

定義式（2）為標準激勵系統，其響應只與步行荷載曲線的形式有關，與行人體重、振型質量無關。基于式（2）的加速度反應譜計算步驟為：①計算320條實測步行荷載曲線作用下標準激勵系統的加速度響應時程·Y·。峰值響應或均方根響應常被用來評估振動舒適jk度［16］，峰值響應具有偶然性，因此本文取計算響應的10 s均方根值的最大值作為當前樓蓋頻率的反應譜值。①調整樓蓋頻率重復以上計算，得到樓板頻率－10 s加速度均方根值反應譜曲線。計算時取板跨42 m，步幅0.75 m，一階振型。

圖3為1.84 Hz步頻、阻尼比2%時的反應譜，圖中用豎向虛線標出了步頻及其倍頻的位置。可見反應譜不僅在步頻及其倍頻處有峰值，在半步頻及其倍數處也有峰值，這是因為計算采用的復步步行荷載曲線，進一步說明了采用實測步行荷載的重要性。

對于給定阻尼比ξk，共有320條反應譜，對其任意頻率fi處的反應譜值（共320個），取95%分位數處的譜值ai作為此頻率處的代表值，將所有（fi，ai）連線作為ξk對應的反應譜曲線，以下稱為標準反應譜曲線。圖4為按上述步驟獲得的1%阻尼比的均方根反應譜（圖中虛線）。圖5給出了對應阻尼比為1%～5%的五條標準反應譜曲線。

圖3 標準激勵系統的加速度均方根值反應譜（步頻1.84 Hz，阻尼比2%）Fig.3 RMS acceleration response spectrum of the generalized excitation system（walking rate＝1.84 Hz，ξk＝2%）

圖4 1%阻尼比標準反應譜曲線Fig.4 Standard acceeration response spectrum（1%damping）

圖5 不同阻尼比的標準反應譜曲線Fig.5 Standard acceeration response spectrum（1%～5%damping ratio）

1.3 加速度均方根反應譜公式

圖5所示反應譜曲線峰值集中在2 Hz左右，通過曲線擬合方式獲得其數學模型非常困難。針對此問題，建議綜合運用頻率、振動幅值雙控原則，可只對曲線3 Hz以上部分進行擬合。實際樓蓋設計時，首先保證樓蓋的自振頻率不低于3 Hz的常用限值，進而再利用反應譜公式驗算加速度響應。據此，對于3 Hz以上部分建議的標準反應譜計算公式為：

式中：f為樓蓋頻率，單位Hz；a，b為模型參數。將上式擬合圖5中各阻尼比對應的反應譜計算曲線，得模型參數見表1。

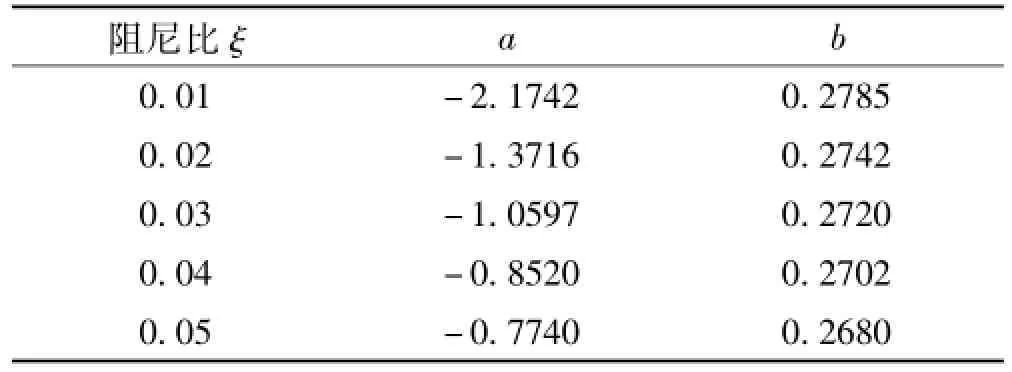
表1 標準反應譜模型參數系數Tab.1 Coefficients of standard acceleration response spectrum

圖6 不同阻尼比下擬合的標準反應譜Fig.6 Standard acceleration response spectrum for various damping ratio

當取其他阻尼比值時，譜模型參數按下式計算

各阻尼比下擬合反應譜見圖6。相同頻率時，樓蓋振動幅值隨阻尼比的增大而減小。

2 標準反應譜影響參數及修正方法

本節討論高階振型、邊界條件、計算跨度、步幅等參數對標準反應譜的影響以及對應的修正方法。

2.1 高階振型

以四邊簡支方板為例，計算所得1～3階振型的反應譜見圖7。可見，前3階振型所對應的10 s加速度均方根值反應譜在3 Hz以上區域差別不大，僅在步頻倍頻處略有差別。因此，計算響應時可采用式（3）的標準反應譜公式考慮高階振型的貢獻。此結論對于其他四種邊界條件：對邊簡支對邊固定、三邊簡支一邊固定、對邊簡支一邊固定一邊自由、三邊簡支一邊自由也成立［17］。

圖7 四邊簡支邊界對應的前三階反應譜Fig.7 Response spectrum for the first three vibrationsmodes of imply supported square plate

2.2 邊界條件

圖8比較了五種邊界條件下一階振型對應的反應譜曲線，圖中字母S、C、F分別表示簡支、固定和自由邊界。可見，若以四邊簡支（S：S－S：S）邊界對應的反應譜為基準，三邊簡支一邊自由（S：S－S－F）邊界對應反應譜與之差異最大，峰值差約20%，其余各邊界對應反應譜則差別不大。由于邊界條件對譜峰值的影響主要出現在3 Hz以前，對不同邊界條件采用統一的反應譜曲線（即式（3）對應的四邊簡支邊界標準反應譜）可行，給計算使用帶來極大的方便。

圖8 各邊界條件一階反應譜比較Fig.8 Effect of boundary conditions on the acceleration response spectrum

2.3 計算跨度

為考慮樓蓋計算跨度的影響，按最小跨度16.5 m，最大跨度42 m，間隔1.5 m，計算了5種阻尼比下各跨度對應反應譜。然后將各跨度在四種固定步頻曲線作用下的反應譜除以對應42 m跨度的反應譜，再對各比值求均值得到某一步頻荷載在某一阻尼比下的跨度修正系數，總共得到20條（4種步頻×5種阻尼比）跨度修正系數曲線。對20條曲線的均值進行擬合（圖9），得到如下跨度修正系數表達式：

式（5）表明跨度較小時對響應影響較大，隨跨度的增大其影響越來越小，當跨度大于30 m時，修正系數已大于0.95，因此對于跨度大于30 m的樓蓋不考慮跨度修正不會導致太大誤差。

圖9 跨度修正系數均值及擬合值Fig.9 Correction coefficient for floor span

2.4 步幅

根據對實測4 300多組［步頻、步距］數據的統計［13］，步幅均值隨步頻的變化很小，穩定在0.66 m左右。相同樓蓋跨度，步幅大小影響步行荷載的時長。因此，可將步幅修正與樓蓋跨度修正統一以方便計算，即當步幅不同于0.75 m時，直接將式5中的跨度乘以0.75/dl修正，即得到下式

式中：dl為步幅，L為計算跨度，單位為m。

為說明式（6），計算了相同步頻、2%阻尼比下0.75、0.66、0.62 m三種步幅在12 m、42 m兩個跨度下的標準反應譜曲線。進而計算0.75、0.66 m的反應譜與0.62 m反應譜比值的均值，結果見表2。表中同時給出了由式（4）、（6）計算所得比值，采用跨度與步幅統一修正的式（6）結果誤差很小，在2%以內。

表2 不同步幅對應反應譜比較Tab.2 Comparison of spectrum with different stride length

2.5 阻尼比

取步頻為1.9 Hz的步行荷載，四邊簡支邊界，阻尼比0.01∶0.01∶0.05，計算10 s加速度均方根值反應譜，見圖10。在共振區域（步頻的倍頻及半倍頻處）阻尼比值影響較大，阻尼比大時步行荷載中的高頻成分影響減小。后續實例對比也表明，樓蓋阻尼比取值對振幅的估計有較大的影響，需謹慎對待。由于微振時結構中許多阻尼機制（如節點、內摩擦等）貢獻甚微，結構適用性驗算的阻尼比取值應比安全性驗算的阻尼比低。

圖10 阻尼比對反應譜的影響Fig.10 The influence of damping

3 基于加速度反應譜的樓蓋響應計算

利用上一小節建立的標準反應譜曲線以及影響參數的修正方法，可通過以下四個步驟計算樓蓋的10 s加速度均方根響應：

（1）利用有限元建模等方法計算目標樓蓋的各階振動頻率fjk及振型質量Mjk。

（2）由式（3）計算每階振型對應的加速度反應譜值，即：

式中：fjk為樓蓋（j，k）階振型頻率，系數a、b根據樓蓋阻尼比按表1或式（4）取值。j為板沿與行走路線垂直方向振型階數，k為板沿行走路線方向振型階數。

（3）按下式計算每階振型對應的10 s加速度均方根值響應。

式中：φwjk為行走路線對應的第（j，k）階振型值，φjk為板上響應驗算點處（j，k）階振型值，參考加速度arefjk＝G/Mjkajkref＝G/Mjk，G為行人體重，單位N，Mjk為樓蓋（j，k）階振型質量。

（4）對步驟3計算所得的響應按平方法和開平方的方式進行組合。

4 實例應用分析

4.1 實例結構與人致激勵振動實驗

某市體育中心綜合訓練館采用預應力混凝土樓蓋（圖11紅框部分），短邊方向跨度為41.55 m，布置有10根450×3000 mm的預應力混凝土梁；長邊方向72 m，共9跨，間距8 m；混凝土板厚120 mm，梁板采用C50混凝土澆筑。作者在此大跨度樓蓋上安裝了一套包括12個加速度傳感器的豎向振動測試系統，用于檢驗和監測樓蓋的豎向振動特性與振動幅度，自2009年初正常工作至今。儀器安裝情況與具體布設位置見圖12。

圖11 混凝土大跨樓蓋與步行試驗路線Fig.11Walking routes

圖12 樓蓋測點布置Fig.12 Arrangement ofmeasuring points

利用振動監測系統開展了各種不同人致激勵下樓蓋振動的多組測試［18］，其中開展了單人固定步頻的實驗，實測結構響應可用于驗證本文建議反應譜方法的合理性。

測試者體重80 kg，在節拍器的引導下按固定步頻2 Hz沿四條路線進行了單人激勵的振動測試。四條行走路線分別為沿樓蓋短軸中線行走測試（路線1）；沿長軸中線行走測試（路線2）；以及分別沿樓蓋兩個對角線方向行走測試（路線3，4）。線路示意見圖11。

4.2 樓蓋中心的響應計算

采用Ansys軟件建模計算樓蓋前16階豎向振型頻率及振型質量［16］，結果見表3。阻尼比取2%，按表1確定反應譜計算公式：

對樓蓋中心點，由于長邊及短邊方向為偶數個半波的振型（比如第2，8階）在該處的振型值為0，因此這些振型對響應無影響，計算時可略去。樓蓋各階振型對應的樓蓋中心點加速度響應及各振型響應組合見表4～表5對參與組合的振型階數，令組合響應不小于總響應的95%，由表5可見，組合至第5、7階豎向振型時，樓蓋響應分別為組合至第14階振型樓蓋響應的94.6%、98.3%。因此，考慮樓蓋前7階振型能保證組合響應有足夠的精度。按照反應譜方法計算得到的樓蓋中心點響應為0.117 cm/s2。

4.3 所有測點不同行走線路對比

反應譜計算的樓蓋中心點響應為0.117 cm/s2，略小于按路線2行走實測值0.129 cm/s2，原因可能是樓蓋阻尼比取值有偏差。為此，取樓蓋阻尼比為0.01、0.02、0.03三種情況，采用反應譜方法計算了對應線路1和線路2的所有測點處的加速度響應，并在圖13～圖14中與實測結果進行了對比。

實測數據表明，沿線路1（圖13）、線路2（圖14）的步行激勵所引起的樓蓋響應幅值大于線路3、4的響應，因此按最不利行走路線進行樓蓋振動舒適度驗算是合理的。圖13、14結果同時表明，絕大部分實測點的響應在阻尼比0.01～0.03的計算值之間，本文建議的反應譜計算方法可行。考慮到微振時結構阻尼小，樓蓋振動舒適度驗算時應取較小的阻尼比值。對本例的預應力混凝土樓蓋，由于其上沒有任何的分割墻，取阻尼比1%或1.5%是合理的。

表3 樓蓋各階頻率及振型質量Tab.3 Natural frequency and modalmass

表4 樓蓋中心點各階振型響應Tab.4 Response of cen tral point of floor

表5 樓蓋中心點各階振型響應組合Tab.5 Modal response combination of central point of floor

圖13 各測點響應計算與實測值比較（路線1）Fig.13 Comparison ofmeasured response and calculated results（route 1）

圖14 各測點響應計算與實測值比較（路線2）Fig.14 Comparison ofmeasured response and calculated results（route 2）

4.4 與CSTR43規范計算結果對比

圖13～圖14中另外加入按英國CSTR43計算結果的比較，圖中帶標記C的為按CSTR43計算結果，考慮阻尼比1%和3%兩種情況。除去1、9、11號點外，其他各測點采用CSTR43的計算結果均小于實測結果。原因可能在于樓蓋第三階振型（頻率6.09 Hz，與3倍步頻接近）在1、9、11測點處的振型值分別為1.0，1.0和0.434，而在其余測點均接近0。顯然，采用CSTR43時步頻的選擇對結果影響很大。文獻［19］也曾指出CSTR43的計算結果不可靠。

5 結 論

本文利用實測中國人步行荷載曲線，利用振型分解法研究步行激勵下大跨樓蓋的加速度10 s均方根反應譜。依據頻率和響應的雙控原則提出了適用于基頻3～20 Hz（或跨度16～42 m）的單人步行荷載激勵下的樓蓋響應反應譜計算公式，討論并給出了高階振型、邊界條件、計算跨度、行走步幅以及阻尼比取值等要素的影響和修正方法。最后通過與已建大跨樓蓋步行激勵下實測加速度響應的比較，驗證了建議反應譜計算結果的合理性，可供大跨混凝土樓蓋振動舒適度設計與振動評估參考使用。

［1］宋志剛，金偉良.行走激勵下大跨度樓板振動的最大加速度響應譜方法［J］.建筑結構學報，2004，25（2）：57－63.

SONG Zhi-gang，JIN Wei-liang.Peak acceleration response spectrum of long span floor vibration by pedestrian excitation［J］.Journal of Building Structures，2004，25（2）：57－63.

［2］聶建國，陳宇，樊健生.步行荷載作用下單跨人行橋振動的均方根加速度反應譜法［J］.土木工程學報，2010，43（9）：109－116.

NIE Jian-guo，CHEN Yu，FAN Jian-sheng.RMS acceleration response spectrum method for single-span footbridges under pedestrian load［J］.China Civil Engineering Journal，2010，43（9）：109－116.

［3］Willford M，Young P，Field C.Improved methodologies for the prediction of footfall－induced vibration：Proceedings of the SPIE-The International Society for Optical Engineering Buildings for Nanoscale Research and Beyond，31 July 2005，USA，2005［C］.SPIE-The International Society for Optical Engineering.

［4］陳宇，樊健生，聶建國.多跨人行橋振動的均方根加速度反應譜法［J］.土木工程學報，2010，43（9）：117－124.

CHEN Yu，FAN Jian-sheng，NIE Jian-guo.RMS acceleration response spectrum method for multi-span footbridges under pedestrian load［J］.China Civil Engineering Journal，2010，43（9）：117－124.

［5］韓小雷，陳學偉，毛貴牛.基于人群行走仿真的樓板振動分析方法及反應譜公式推導［J］.建筑科學，2009，25（5）：4－9.

HAN Xiao-lei，CHEN Xue-wei，MAO Gui-niu.Research on analysismethod for floor vibration and formula derivation of response spectra baded on simulation of crowd walking［J］.Building Science，2009，25（5）：4－9.

［6］Ungar E E，Zapfe JA，Kemp JD.Predicting footfall-induced vibrations of floors［J］.Sound and Vibration，2004，38（11）：16－22.

［7］Ungar E E.Vibration criteria for sensitive equipment：Proceedings Internoise［C］.Toronto，Canada，1992.

［8］Galbraith FW，Barton MV.Ground loading from footsteps［J］.The Journal of the Acoustical Society of America，1970，48（2）：1288－1292.

［9］Mouring SE.Dynamic response of floor systems to building occupant activities［D］.Johns Hopkins University，1992.

［10］袁剛，張木勛，王中琴，等.正常人足底壓力分布及其影響因素分析［J］.中華物理醫學與康復雜志，2004，26（3）：156－159.

YUAN Gang，ZHANG Mu-xun，WANG Zhong-qin，et al.The distribution of foot pressure and its influence factors in Chinese peop le［J］.Chinese Journal of Physical Medicine and Rehabiliation，2004，26（3）：156－159.

［11］湯榮光.正常人足底靜態和動態壓力分布的測定［J］.中國生物醫學工程學報，1994，13（2）：175－177.

TANG Rong-guang，Static and dynamic pressure distribution under normal feet［J］.Chinese Journal of Biomedical Engineering，1994，13（2）：175－177.

［12］王明鑫，俞光榮，陳雁西，等.正常中國成年人足底壓力分析［J］.中國矯形外科雜志，2008，16（9）：687－690.

WANG Ming-xin，YU Guang-rong，CHEN Yan-xi，et al.Analysis of plantar pressure distribution of the normal Chinese adult［J］.Orthopedic Journal of China，2008，16（9）：687－690.

［13］彭怡欣.基于三維步態分析技術的步行荷載實驗建模研究［D］.上海：同濟大學，2012.

［14］陳雋，葉艇，彭怡欣.拓展步行荷載對樓板振動響應影響的對比研究［J］.振動與沖擊，2012，31（18）：55－59.

CHEN Jun，YE Ting，PENG Yin-xin.A comparison study on methods for expanding a single foot-falling load curve based on floor responses［J］.Journal of Vibration and Shock，2012，31（18）：55－59.

［15］Chen Jun.Peng Yi-xin，Ye Ting.Onmethods for extending a single footfall trace into a continuous force curve for floor vibration serviceability analysis［J］.Structural Engineering and Mechanics，2013，46（2）：179－196.

［16］Reynolds P，Pavic A.Vibration performance of a larqe cantilever grandstand during an international football match［J］.J.of Performance of Constructed Facilities，2006，20（3）：202－212.

［17］葉艇.步行荷載作用下大跨度混凝土樓蓋加速度反應譜研究［D］.上海：同濟大學，2012.

［18］折雄雄.大跨度混凝土梁板樓蓋振動舒適度實測與理論分析研究［D］.上海：同濟大學，2010.

［19］Pavic A，Reynolds P，Waldron P，et al.Critical review of guidelines for checking vibration serviceability of posttensioned concrete floors［J］.Cement and Concrete Composites，2001，23（1）：21－31.

Acceleration response spectrum of a long span floor under human walking loads

CHEN Jun1，2，YE Ting2，PENG Yi-xin2，3
（1.State Key Laboratory of Disaster Reduction in Civil Engineering，Shanghai200092，China；
2.TongjiUniversity，Shanghai200092，China；3.The Hong Kong Polytechnic University，Hong Kong，China）

Here，the acceleration response spectrum of a long span floor under human walking loads was studied.Three hundreds and twenty experimentalmeasurements ofwalking load curveswere applied to a long span floor to obtain a 10-second root-mean-square acceleration response spectrum in the vertical vibration direction，based on it a simplified calculation expression was suggested for the root-mean-square acceleration response of the floorwithin the frequency range of3－20Hz.The effects of several parameters including higher order vibration modes，boundary condition，floor span，stride length and damping ratio on the spectrum were studied and the corresponding modifying measures were suggested.The detailed implementation procedure of the suggested response spectrum was presented.The feasibility and applicability of the suggested spectrum were validated by comparing the prediction results with field measurements of an existing long span floor.

human walking loads；long span concrete floor；RMS acceleration response spectrum；parametric analysis

T312＋.1

A

10.13465/j.cnki.jvs.2014.24.001

國家自然科學基金（51178338，51478346）；土木工程防災國家重點室（SLDRCE14－B－16）

2013－07－16 修改稿收到日期：2014－01－02

陳雋男，博士，教授，1972年4月生