基于動態自學習閾值和趨勢濾波的機械故障智能預警方法

張 明，馮 坤，江志農

（北京化工大學診斷與自愈工程研究中心，北京100029）

基于動態自學習閾值和趨勢濾波的機械故障智能預警方法

張 明，馮 坤，江志農

（北京化工大學診斷與自愈工程研究中心，北京100029）

針對當前機械在線監測系統報警難以實現機械故障早期預警問題，提出一種智能預警方法。基于在線監測系統大量監測數據統計分析，采用動態的自學習閾值算法計算預警閾值，并應用l1趨勢濾波技術消除隨機誤差獲取濾波后的趨勢。應用動態自學習閾值替代監測系統中的常規報警閾值，比較自學習預警閾值與濾波后的趨勢，實現了機械故障早期預警。工程實例表明，該方法能夠對機械故障實現早期預警，對預防機械事故的發生有重要的作用。

自學習閾值；故障預警；非參數檢驗；beta分布；l1趨勢濾波

汽輪機、發電機、壓縮機等是石化、電力等流程工業中廣泛使用的機械，該類設備安全、穩定的運行，會產生良好的經濟效益和社會效益。目前，企業中的大型關鍵設備多數已安裝機械在線監測系統，但是，當前的機械在線監測系統并不能實現機械故障的早期預警，主要因為存在以下問題：①報警閾值由主機廠提供并預先設定到監測系統中，當機組報警時故障已經惡化到一定程度，并不能在故障發生的早期實現預警；②若為了使監測系統實現早期預警而將報警閾值調低，則可能會因噪聲及采集誤差的影響使實時采集的監測數據反復穿越報警線，導致大量錯誤預警；③若采用傳統平滑濾波技術消除噪聲及采集誤差的影響，則有可能丟失關鍵故障信息，從而產生嚴重事故，給企業帶來巨大損失。

研究能夠充分利用機械在線監測系統的監測參數數據解決上述問題的機械智能預警技術［1］是現實的迫切需要，具有重要的工程意義，同時對推進機械在線監測系統走向智能化具有理論指導意義。

1 智能預警方法的提出

機械在線監測系統當前常規報警方式為：預先設定測點的報警值與危險值（固定值，參考API、ISO等標準），將實時采集的特征值數據與預先設定的報警值與危險值進行比較，若實時數據小于報警值，則判定機組運行正常；若實時數據大于報警值且小于危險值，則判定機組發生故障，此時需要排查故障原因并判定是否需要停車維修；當實時數據大于危險值，則需要立即停車維修。

如圖1所示，機械在線監測系統常規報警方式十分簡單，未能利用監測參數趨勢數據，當超過報警值時機械故障往往已經惡化，研究能夠充分利用監測參數趨勢數據的智能預警技術是非常必要的。國內外諸多學者對預測故障的智能報警技術進行了研究，Dokas等［2］研究了基于故障樹分析和模糊專家系統的預警診斷技術；Widarsson等［3］研究了回收鍋爐泄漏故障的貝葉斯神經網絡預警診斷方法；Zhao等［4］研究了市政固體廢物焚化爐在線早期故障監測與診斷方法；馬晉等［5］研究了基于瞬時轉速波動率實現了內燃機點火狀態的早期預警方法；魏中青等［6］研究了快變報警技術實現了大型旋轉機械突發性故障的早期預警診斷；張棟梁等［7］研究了狀態監測系統中的智能預警管理系統。

圖1 常規報警判斷流程圖Fig.1 General alarm flow chart

本文基于監測參數趨勢數據統計分析提出了自學習預警閾值與趨勢濾波相結合的機械故障智能預警方法。研究了動態自學習預警閾值算法，實現監測參數預警閾值的自動學習；使用Kim等提出的l1趨勢濾波技術［8］對監測參數趨勢數據進行濾波，消除了趨勢數據中的采集誤差。

2 監測參數趨勢數據的統計分析

選取了卡方檢驗（Chi-square test）、Kolmogorov-Smirnov檢驗及秩和檢驗，對機械在線監測系統不同測點的監測參數趨勢數據進行了非參數檢驗［9］。結果表明：平穩狀態下監測參數趨勢趨數據不服從高斯分布，并且同一機組的不同測點監測數據也不能認為來自同一總體。

2.1 卡方檢驗

假設一個定性變量Y具有k個可能取值或有k種分類（標為1，2，…，k），Y的概率分布自然地由概率函數P（Y＝i）（i＝1，2，…，k）所確定。現在要考查已觀察到的一組樣本（容量為n）與某確定的分布G擬合的程度，相當于研究P（Y＝i）（i＝1，2，…，k）與G之間的差異，看這個差異是否屬于偶然變異，這就是卡方檢驗的基本原理。卡方檢驗的步驟如下：

其中：Oi表示落入第i組的樣本觀測值的實際頻數，表示理論頻數。

（3）作出判斷

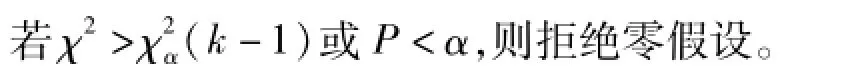
2.2 Kolmogorov-Sm irnov檢驗

Kolmogorov-Smirnov檢驗用于檢驗一組樣本觀測結果的經驗分布同某一指定的理論分布（如高斯分布）之間是否一致。K－S檢驗的基本思路為，將順序分類數據的理論累計頻率分布同觀測的經驗累計頻率分布加以比較，求出他們最大的偏離值，然后在給定的顯著性水平上檢驗這種偏離值是否是偶然出現的。

設理論累計頻數分布為F（x），n次觀測的隨機樣本的經驗分布函數，K－S檢驗的步驟如下：

（1）零假設H0：經驗分布與理論分布沒有顯著差別。

（2）把樣本觀測值從小到大排列為：

x（1），x（2），…，x（n），計算經驗累積分布函數Fn（x）和理論累積分布函數F（x）。

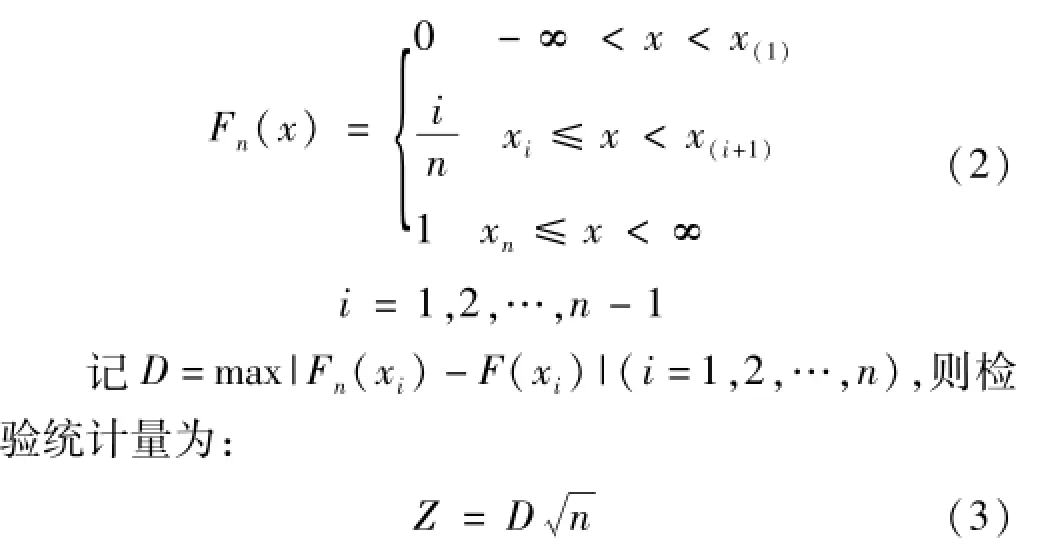
雙側顯著性水平（P值）根據Smirnov提出的公式計算。

（3）作出判斷

若P＜α，則拒絕零假設。

2.3 秩和檢驗

對于分別抽自總體X和Y的兩個獨立樣本，把兩者混合在一起，并按其量值由小到大順序排列，得：

如果xk＝zj，則記Rk（x）?j，則稱為xk在混合樣本中的秩。

設Y的樣本容量n2小于X的樣本容量n1，威爾柯克遜提出用Y在混合樣本中的秩和總和：

來檢驗X和Y的分布是否一致。秩和檢驗的步驟如下：

（1）零假設H0：兩個獨立樣本來自相同的總體。

（2）計算相應檢驗統計量值或P值。

（3）作出判斷

若P＜α，則拒絕零假設。

選取同一機組不同測點的監測參數趨勢數據1和監測參數趨勢數據2，如圖2所示，進行卡方檢驗、Kolmogorov-Smirnov檢驗及秩和檢驗，數據單位為μm。

對監測參數趨勢數據1進行卡方檢驗和Kolmogorov-Smirnov檢驗：

（1）零假設：監測參數趨勢數據1服從高斯分布；

（2）卡方檢驗計算P1＝2.595×10－4，Kolmogorov-Smirnov檢驗計算P2＝7.166 4×10－307；

（3）在顯著性水平α＝0.05時，P1＜α，P2＜α，則兩種檢驗均拒絕零假設，因此監測參數趨勢數據1不服從高斯分布。

同理，對監測參數趨勢數據2進行卡方檢驗和Kolmogorov-Smirnov檢驗：

（1）零假設：監測參數趨勢數據2服從高斯分布；

（2）卡方檢驗計算P1＝6.095 7×10－8，Kolmogorov-Smirnov檢驗計算p2＝7.166 4×10307；

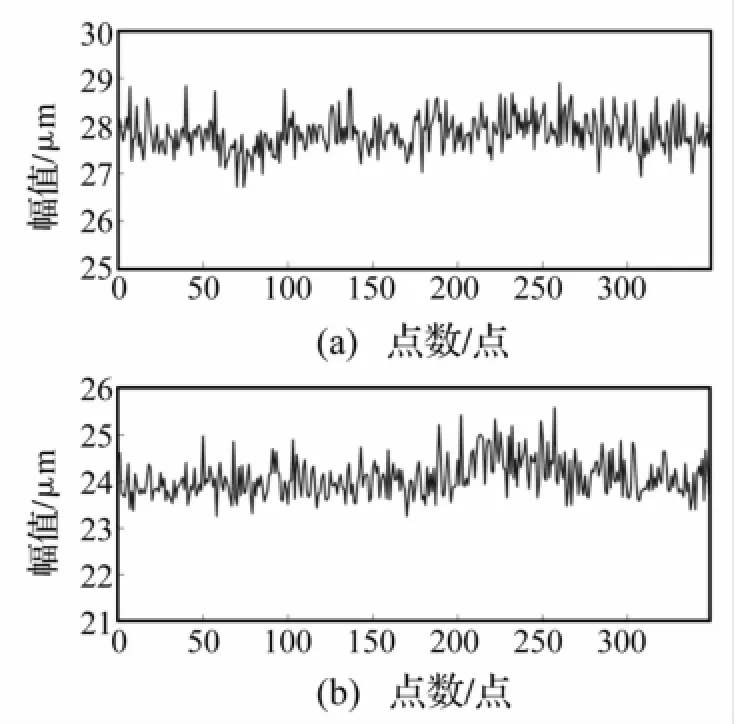
圖2 （a）監測參數趨勢數據1（b）監測參數趨勢數據2Fig.2（a）Monitoring parameters trend data 1（b）Monitoring parameters trend data 2

（3）在顯著性水平α＝0.05時，P1＜α，P2＜α，則兩種檢驗均拒絕零假設，因此監測參數趨勢數據2也不服從高斯分布。

對監測數據參數數據1與數據2進行秩和檢驗：

（1）零假設：監測參數趨勢數據1與數據2來自相同的總體；

（2）秩和檢驗計算P＝1.042 3×10－115；

（3）在顯著性水平α＝0.05時，P＜α，則拒絕零假設，監測參數趨勢數據1和數據2來自不同的總體。

3 基于貝塔分布的預警閾值智能學習方法

近年來國內外對故障診斷自學習報警閾值方法做了諸多研究，Alkaya等［10］研究了基于PCA模型的方差敏感自學習閾值的方法及應用；Raka等［11］研究了基于魯棒自學習閾值的故障監測方法；Shi等［12］做了基于模型的自學習閾值故障監測方法的進一步研究；魏中青等［13］針對往復壓縮機氣閥早期故障預警問題研究了MLE（最大似然估計）閾值規則。

由于監測參數趨勢數據分布不服從高斯分布，并且不同測點的趨勢數據來自不同的總體，說明了不同測點的趨勢數據分布形式不同。基于統計學分析對不同分布特性研究發現：Beta分布是一種多參數統計分布，可以通過調整其多參數逼近任意分布形式，使用貝塔分布分別逼近正常狀態下各測點監測參數趨勢數據的概率密度分布，可得到各測點趨勢數據的貝塔概率密度函數，計算出各測點趨勢數據的預警閾值區間。

3.1 貝塔分布

式中：μx為x的均值；σ2x為x的方差。

當貝塔分布的上限a＝0，下限b＝1時，即成為標準貝塔分布：

貝塔分布密度函數的形狀可由γ，η來控制，其形狀從均勻分布到近似高斯分布，從對稱到不對稱，而且分布在一個有限的范圍內。

3.2 貝塔分布的參數擬合算法

機械在線監測系統的監測參數趨勢數據的概率密度可以通過調整貝塔分布的形狀參數γ，η進行擬合，本文采用最小二乘法進行擬合［14］。

（1）估計概率密度函數

其中：Xi是將樣本數據分區間后，每個區間的中點值；mi是樣本數據落在第i個區間內的個數；n是樣本數據的個數；hi是每個區間的半寬度；N是所有區間的個數。

（2）利用最小二乘法求解形狀參數

其中：Wi為權系數，可根據測量數據情況進行選取；f（Xi，γ，η）為標準貝塔分布的概率密度函數。

3.3 監測參數趨勢數據的預警閾值智能學習算法

在線監測參數數據一般情況下不在0到1的范圍內，所以使用標準貝塔分布擬合監測參數數據的概率密度分布時需要對振動趨勢數據進行歸一化處理。

根據機組平穩運行一段時間后得到的監測參數趨勢數據，計算得到監測參數趨勢數據的概率密度分布，通過最小二乘法擬合求出最逼近實際趨勢數據的貝塔分布形狀參數γ，η，得到趨勢數據的貝塔分布概率密度函數β（γ，η）。預警閾值自學習過程如下：

（1）將一段時間內的監測參數趨勢數據Xi歸一化處理：

Xi為監測參數趨勢數據；Xmin為監測參數趨勢數據中的最小值；Xmax為監測參數趨勢數據中的最大值；X＾i為歸一化后的監測參數趨勢數據；

（2）依據式（9）計算監測參數趨勢數據的概率密度分布；

（3）使用上文提到的最小二乘法擬合監測參數趨勢數據的概率密度分布得到標準貝塔分布的兩個形狀參數γ，η；

α在自學習預警閾值的應用中定義為尖峰噪聲引起的采集誤差。外部影響導致在采集過程中產生的尖峰噪聲的誤差一般情況下為5%［18］，即α＝0.05。在實際應用過程中，可根據采集系統的性能以及傳感器特性調整α值。本文在計算自學習預警閾值時，α取0.05。

選取一組旋轉機械振動趨勢數據，進行預警閾值智能自學習，數據單位為μm（如圖3所示）。按照自學習預警閾值計算方法，取α＝0.05時，使用最小二乘法擬合監測參數趨勢數據的概率密度分布（如圖4（a）所示），得到擬合后的貝塔分布（如圖4（b）所示），貝塔分布兩個形狀參數分別為γ＝34.062 8、η＝46.565 0，計算趨勢數據的閾值下限Threshol d1＝23.009 5、上限Threshol d2＝24.853 8，自學習報警閾值空間［23.009 5，24.853 8］。

圖3 監測參數趨勢數據Fig.3 Monitoring parameters trend data

4 基于l1趨勢濾波技術的機械故障智能預警方法

4.1 趨勢濾波

一個標準的時間序列y1，t＝1，…，n，假設是由一個基本趨勢xt和一個隨機變量zt組成。趨勢濾波就是從標準的時間序列中估計出基本趨勢xt，或者估計出隨

圖4 （a）趨勢數據概率密度分布（b）貝塔概率密度分布Fig.4（a）Trend data probability density distribution（b）beta probability density distribution

機變量zt＝yt－xt。趨勢濾波實際上就是估計一個標準時間序列的基本趨勢xt的過程。

趨勢濾波方法包括：滑動平均濾波［15］，指數平滑濾波［16］，和Hodrick-Prescott（H－P）濾波［17］及l1趨勢濾波［8］等。H－P濾波作為趨勢濾波方法廣泛地應用在許多領域，l1趨勢濾波是在H－P濾波基礎上發展來的，H－P濾波和l1趨勢濾波各有優勢，l1趨勢濾波更適用于分段線性的趨勢的估計。

4.2 l1趨勢濾波

l1趨勢濾波［8］是Kim等在近幾年提出的，是一種H－P濾波的變異，這種改變是使用絕對值（l1范數）和替代了應用在H－P濾波估計趨勢中懲罰變量的平方和。l1趨勢濾波方法和H－P濾波趨勢濾波方法有很多共同的性質，同時還有共同的計算復雜性。兩者根本性不同在于，l1趨勢濾波得到的估計趨勢在分段的線性范圍內更平滑。因此，l1趨勢濾波特別適合分析濾波含有分段線性時間序列的趨勢。實際機械設備故障特征往往表現為趨勢的奇點、斜率的改變等變化，因此l1趨勢濾波恰恰可以檢測和估計這些潛在的變化。

機械在線監測系統中監測參數趨勢數據總會存在一定采集誤差，它會影響機械故障早期預警的準確性。在線監測系統監測參數趨勢數據主要有兩種采集誤差：一種是連續的高斯白噪聲，這種誤差無法絕對避免只能盡量減小；另一種是尖峰噪聲，這種誤差可能是由于系統及傳感器問題造成［18］。使用l1趨勢濾波對監測參數趨勢數據進行濾波處理，能夠很好地得到機組真實的振動趨勢，同時消除了采集誤差對機械故障早期預警的影響。

4.2.1 l1趨勢濾波算法

l1趨勢濾波算法是在H－P濾波基礎上進行改進的新型濾波算法。這種趨勢估計是通過最小化加權目標函數實現的，加權目標函數見式（15）：

λ是一個非負參數用來控制x的平滑性和平衡余項的大小。加權目標函數對x來說是一個嚴格的凸函數，所以只有一個最小值，用xlt表示，因此xlt就是濾波后的趨勢。

文獻［8］指出，l1趨勢濾波求解問題可以等同于對正則化l1最小二乘求解問題，

通過最小二乘法求得此問題結果θlt，則l1趨勢濾波結果xlt＝Aθlt。

4.2.2 l1趨勢濾波仿真研究

模擬葉片脫落故障原始趨勢如圖5（a）所示，在原始趨勢的基礎上添加噪聲如圖5（b）所示，分別使用l1趨勢濾波和H－P趨勢濾波方法對葉片脫落故障的模擬信號進行濾波。調整l1趨勢濾波和H－P趨勢濾波控制系數λ，保證擬合誤差（即：時間序列余項zt＝ytxt二范數的均值）相等的情況下，得到圖5所示濾波結果，擬合誤差為0.141 9。對比圖5中（c）、（d）兩圖，看出l1趨勢濾波能夠更好地估計出實際機械設備突發型故障特征趨勢。

5 本文方法在線監測系統中的工程應用研究

機械智能預警方法將動態自學習預警閾值算法與l1趨勢濾波技術相結合，具體步驟如下：

（1）依據動態自學習預警閾值算法計算平穩運行階段監測參數趨勢數據的動態自學習預警閾值。

（2）使用l1趨勢濾波技術對監測參數趨勢數據進行濾波處理。

圖5 （a）葉片脫落原始趨勢（b）葉片脫落原始趨勢＋噪聲（c）l1趨勢濾波后的趨勢（d）H－P趨勢濾波后的趨勢Fig.5（a）Original trend（b）Original trend＋noise（c）l1 filtering trend（d）H－P filtering trend

（3）將實時濾波后的監測參數趨勢數據與計算得到的動態自學習預警閾值進行比較，如果趨勢數據超出閾值范圍則預警。

下面選取國內某石化企業透平壓縮機在線監測系統中緩變故障案例和突變故障案例驗證本文方法。

5.1 工程案例一

某石化企業煙氣輪機的常規報警值為80μm、危險值為100μm。該機組某測點監測趨勢從2012年6月初開始緩慢爬升，在此之前該測點趨勢一直平穩在73 μm左右，到2012年7月初爬升到95μm左右，一個月內趨勢異常爬升了22μm。排查故障原因發現煙氣中含有了催化劑，使得煙機葉片上逐漸粘附催化劑導致不平衡量逐漸增大，導致趨勢發生緩慢爬升。

根據動態自學習預警閾值算法計算正常運行階段的動態自學習預警閾值，取α＝0.05時，得到擬合后的貝塔分布的兩個形狀參數分別為γ＝2.725 6、η＝2.419 1，趨勢數據的預警閾值下限Threshol d1＝70.790 5、上限Threshol d2＝73.698 5，自學習預警閾值空間［70.790 5，73.698 5］。使用l1趨勢濾波技術對趨勢數據進行濾波處理。當該機組實時濾波后的趨勢數據超出動態自學習預警閾值空間后發出預警。

如圖6所示，使用常規報警方式發出報警時，故障已經惡化到一定程度。與常規報警方式相比，機械智能預警方法在緩變故障發生的早期就可以發出預警，實現了緩慢變化故障早期預警，彌補常規報警方式在緩變故障預警上的不足。

5.2 工程案例二

某石化企業二氧化碳壓縮機的常規報警值為60 μm，危險值為90μm。該機組在正常運行過程中突然發生異常，在5 s的時間里振動趨勢從40μm左右跳變到50μm左右。事后排查故障原因發現壓縮介質不干凈，在長期運行過程中污垢在葉片上積累，污垢脫落瞬間導致轉子不平衡量突然變化，從而導致趨勢突變。

根據動態自學習預警閾值算法計算正常運行階段的動態自學習預警閾值，取α＝0.05時，得到擬合后的貝塔分布的兩個形狀參數分別為γ＝1.918 1、η＝2.642 5，趨勢數據的預警閾值下限Threshol d1＝34.953 2、上限Threshol d2＝41.717 7，自學習預警閾值空間［34.953 2，41.717 7］。使用l1趨勢濾波技術對趨勢數據進行濾波處理。當該機組實時濾波后的趨勢數據超出動態自學習預警閾值空間后發出預警。

圖6 （a）緩變故障原始趨勢（b）l1濾波后緩變故障趨勢Fig.6（a）Original trend of slowly changed fault（b）l1 filtering trend of slowly changed fault

圖7 （a）突變故障原始趨勢（b）l1趨勢濾波后突變故障趨勢Fig.7（a）Original trend of fast changed fault（b）l1 filtering trend of fast changed fault

如圖7所示，本例突變故障并沒有觸發常規報警。與常規報警相比，機械智能預警方法在突變故障發生的早期就可以發出預警，實現了突然變化故障早期預警，彌補常規報警方式在突變故障預警上的不足。

6 結 論

本文提出基于自學習預警閾值和趨勢濾波的機械故障智能預警方法，得到如下結論：

（1）對監測參數趨勢數據進行非參數檢驗，驗證了趨勢數據并不服從高斯分布并且不同測點的趨勢數據來自不同總體。

（2）使用貝塔分布擬合不同測點監測參數趨勢數據的概率密度分布，并提出了動態自學習預警閾值算法。利用l1趨勢濾波技術消除了監測參數趨勢數據中的采集誤差。

（3）提出機械智能預警方法為：將實時l1趨勢濾波后的監測參數趨勢數據與動態自學習預警閾值進行比較，如果趨勢數據超出閾值范圍則預警。

工程案例表明：機械智能預警方法能夠彌補常規報警方式在早期故障預警方面的不足，在故障發生的早期尚未觸發常規報警時就可以監測到趨勢異常從而實現早期預警。

［1］高金吉.機械故障診治與自愈化［M］.北京：高等教育出版社，2012.

［2］Dokas IM，Karras D A，Panagiotakopoulos D C.Fault tree analysis and fuzzy expert systems：Early warning and emergency response of landfill operations［J］.Environmental Modelling＆Software，2009，24（1）：8－25.

［3］Widarsson B，Dotzauer E.Bayesian network-based earlywarning for leakage in recovery boilers［J］.Applied Thermal Engineering，2008，28（7）：754－760.

［4］Zhao JS，Huang JC，Sun W.On-line early fault detection and diagnosis of municipal solid waste incinerators［J］.Waste Management，2008，28（11）：2406－2414.

［5］馬晉，江志農，高金吉.基于瞬時轉速波動率的內燃機故障診斷方法研究［J］.振動與沖擊，2012，31（13）：119－124.

MA Jin，JIANG Zhi-nong，GAO Jin-ji.Diesel engine fault diagnosis method based on instantaneous angular speed fluctuation ratio［J］.Journalof Vibration and Shock，2012，31（13）：119－124.

［6］魏中青，馬波，江志農，等.旋轉機械振動監測快變報警系統研究及工程應用［J］.機電工程技術，2010，39（12）：82－84，114.

WEIZhong-qing，MA Bo，JIANG Zhi-nong，et al.Rotating machinery vibration monitoring fast changing alarm systems research and engineering applications［J］.Mechanical＆Electrical Engineering Technology，2010，39（12）：82－ 84，114.

［7］張棟梁，魏中青.基于狀態監測的預警管理系統研究與應用［J］.電子設計工程，2011，12：8－10，14.

ZHANG Dong-liang，WEIZhong-qing.Study and application of early warning management system based on condition monitoring［J］.Electronic Design Engineering，2011，12：8－10，14.

［8］Kim S J，Koh K，Boyd B，et al.l1 Trend filtering［J］.SIAMReview，Problems and Techniques Section，2009，51（2）：339－360.

［9］宋昕，蔡泳，徐剛，等.非參數檢驗方法概述［J］.上海口腔醫學，2004，13（6）：561－563.

SONG Xin，CAI Yong，XU Gang，et al.A review of nonparametric test［J］.Shanghai Journal of Stomatology，2004，13（6）：561－563.

［10］Alkaya A，Eker I.Variance sensitive adaptive thresholdbased PCA method for fault detection with experimental application［J］.ISA Transactions，2011，50（2）：287－302.

［11］Raka S A，Combastel C.Fault detection based on robust adaptive thresholds：A dynamic interval approach［J］.Annual Reviews in Control，2013，37（1）：119－128.

［12］Shi Z，Gu F，Lennox B，et al.The development of an adaptive threshold for model-based fault detection of a nonlinear electro-hydraulic system［J］.Control Engineering Practice，2005，13（11）：1357－1367.

［13］魏中青，馬波，竇遠，等.基于MLE閾值規則的小波特征提取技術在氣閥故障診斷中的應用［J］.振動與沖擊，2011，30（1）：237－241.

WEIZhong-qing，MABo，DOU Yuan，etal.Wavelet feature extracting technique based on maximum likelihood estimation threshold rule and its application in fault diagnosis of a gas valve［J］.Journal of Vibration and Shock，2011，30（1）：237－241.

［14］曹天捷，周則恭.最小二乘法在估計概率分布參數中的應用［J］.機械強度，1997（4）：34－37.

CAO Tian-jie，ZHOU Ze-gong.Application of the least square method in the estimation of the parameters of the probability distribution［J］.Journal of mechanical strength，1997（4）：34－37.

［15］Jose A R，Eduardo R，Juan C E.Detrending fluctuation analysis based on moving average filtering［J］.Physica A：Statistical Mechanics and its Applications，2005，354：199－219.

［16］Taylor J W.Exponential smoothing with a damped multiplicative trend［J］.International Journal of Forecasting，2003，19（4）：715－725.

［17］Hodrick JR，Prescott C E，Postwar U S.Business cycles：An empirical investigation［J］.Journal of Money，Credit and Banding，1997，29（1）：1－29.

［18］Chen Z，Ivanov P C，Hu K，et al.Effect of nonstationarities on detrended fluctuation analysis［J］.Physical Review E，2002，65（4）：041107.

A mechanical fault early warning methodology based on dynamic self-learning threshold and trend filtering techniques

ZHANGMing，FENG Kun，JIANG Zhi-nong
（Diganosis＆Self-Recovery Engineering Research Center，Beijing University of Chemical Technology，Beijing 100029，China）

Because the alarm mode of current online monitoring systems is hard to realize early-warning a mechanical fault，an early warning methodology was proposed here.Based on statistical analysis ofmass data in online monitoring systems，advantages of the dynamic self learning threshold algorithm were taken to calculate a warning threshold，and the l1 trend filtering technology was used to gain the filtered trend eliminating random errors.With dynamic self-learning threshold instead of general alarm threshold in monitoring systems，early warning of a fault could be acquired by comparing the self-learning warning threshold and the filtered trend.Itwas shown from engineering examples that early warning of amechanical fault can be achieved with the proposed method，it plays an important role in preventing occurrence ofmechanical fault.

self-learning threshold；fault early warning；nonparametric test；beta distribution；l1 trend filtering

TH165＋.3；TP391

A

10.13465/j.cnki.jvs.2014.24.002

國家自然科學重點基金項目（51135001）；國家青年科學基金項目（51305020）；國家重點基礎研究發展計劃（“973”計劃）項目（2012CB026000）

2013－10－21 修改稿收到日期：2014－01－02

張明男，博士生，1988年7月生

江志農男，教授，博士生導師，1967年10月生