大型可展開天線與衛星的熱致耦合動力學分析

楊癸庚，朱敏波，連培園，高 峰，宗亞靂

（西安電子科技大學電子裝備結構設計教育部重點實驗室，西安 710071）

大型可展開天線與衛星的熱致耦合動力學分析

楊癸庚，朱敏波，連培園，高 峰，宗亞靂

（西安電子科技大學電子裝備結構設計教育部重點實驗室，西安 710071）

以帶有大型環形可展開天線的航天器為研究對象，采用有限元法，對大型可展開天線進行了在軌進出陰影區的瞬態溫度求解；并基于衛星－天線剛柔耦合動力學模型，將時變溫度場等效為時變熱載荷加載到天線上，對整星系統的熱致耦合動力學響應進行了數值模擬。結果表明，天線進出陰影期間，自身溫度梯度主要存在于迎光側與背光側之間，并基于此可估算出天線的熱響應特征時間；時變熱載荷會導致天線結構和衛星姿態發生明顯的振動響應，天線結構振動響應主要集中在第一、二階固有模態上，衛星則會發生低頻姿態振蕩運動；該方法可以合理地預測大型可展開天線系統的熱致耦合動力學響應。

可展開天線；熱響應特征時間；衛星－天線剛柔耦合；熱致耦合動力學

隨著航天技術的迅速發展，大型柔性結構和柔性附件廣泛存在于各類航天器中，如太陽帆板、天線支撐臂、大型可展開天線等。航天器在軌運行時，熱載荷為其主要載荷，在航天器進出地球陰影區時，溫度的劇烈變化不僅會使天線等柔性附件發生較大的熱變形，誘發熱致振動，而且擾動力作用還會傳遞到航天器主體上，進而影響航天器的指向精度和姿態穩定性，導致航天器無法正常工作，甚至功能失效，如哈勃空間望遠鏡太陽電池陣熱致振動現象［1］。

自20世紀60年代以來，隨著熱載荷導致衛星失效的實例［1－3］不斷出現，熱致振動問題成為研究的熱點問題之一［4－13］。Boley［4］最早提出熱致振動概念，他將上表面突加恒定熱流的薄板梁中產生的熱彎矩加入梁的動力學方程中，發現當梁的熱特征時間tT［5］與結構響應特征時間tS相接近時，熱能夠誘發明顯的振動。Thornton等［6］在研究HST太陽翼的彎曲振動時，采用簡化的梁模型，研究了結構動力學響應和瞬態溫度場之間的耦合作用。Boley、Thornton等在研究熱致振動機理時，均將實際結構簡化為簡單的梁模型，而可展開天線等大型空間結構并不能進行簡單的簡化，相關的理論分析未見公開報導。大型復雜空間結構熱致振動的數值仿真方面，安翔等［11］對某空間太陽電池陣中央桁架進行了熱－結構耦合動力學數值仿真。楊玉龍等［12］對星載可展開天線進出陰影區時的熱致振動進行了數值分析，但是溫度場是突加在結構上的。劉勁等［13］對可展開天線在半正弦熱沖擊下的熱致振動進行了數值分析。上述學者在進行大型復雜結構的熱致振動數值仿真分析時，總是將溫度作為沖擊施加到結構上，并非真實的在軌瞬態溫度場作用，而且并未考慮天線與衛星之間的剛柔耦合作用。

針對上述大型復雜結構熱致振動數值仿真中的不足之處，本文以大型可展開天線－衛星剛柔耦合系統為對象，詳細分析了天線進出陰影期間的溫度場變化規律，提出了天線熱響應特征時間的估算方法；并基于衛星－天線剛柔耦合動力學模型，對整星系統的熱致耦合動力學響應進行了數值模擬，分析了熱致耦合動力學響應的特點。

1 天線結構的溫度場分析

1.1 溫度場分析的有限元法

根據固體傳熱學，空間可展開天線結構的瞬態溫度場微分方程為

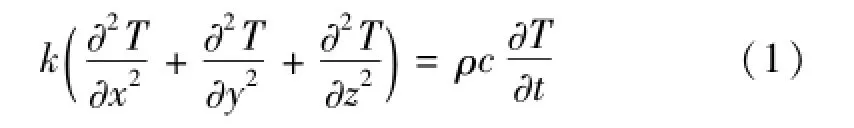
其中：ρ為材料密度，c為比熱容，k為熱傳導系數，T為溫度，t為時間，ε為表面輻射效率，T∞為太空環境溫度，σ為斯蒂芬－波爾茲曼常數，α為表面輻射吸收率，qr為單位面積入射的輻射熱流密度。

對天線結構進行熱有限元離散，經過推導組裝，可以得到整個結構的溫度場有限元方程［14］如下

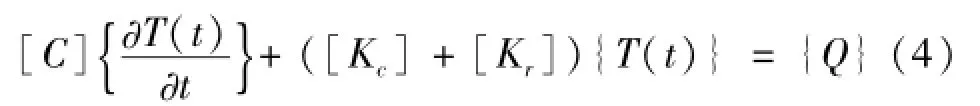
其中：［C］、［Kc］、［Kr］、｛Q｝和｛T（t）｝分別為組裝后整體結構的熱容矩陣、熱傳導矩陣、熱輻射矩陣、熱流載荷向量和節點溫度向量。

對式（4）進行時域差分離散，即可得到t時刻溫度場的計算方程如下

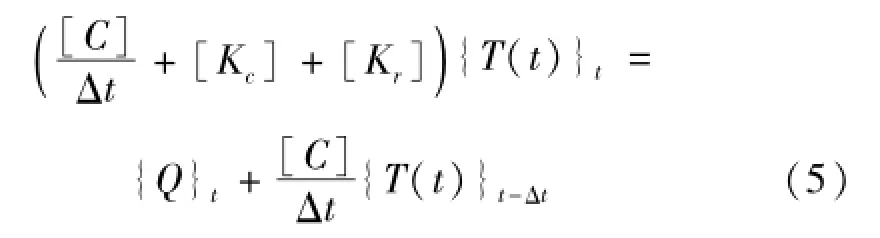
2 星線剛柔耦合動力學模型的建立

對于可展開天線等復雜撓性附件結構，本文建立集中參數模型，用有限元法對系統進行離散化，建立有限自由度的動力學模型；這里考慮到天線與衛星的平動耦合作用與轉動耦合作用相比較小，忽略衛星的平動，系統在質心處約束衛星在三個方向的平動。

2.1 整星運動角動量方程

系統由衛星（中心剛體）和天線（撓性附件）組成，如圖1所示，其中O1x1y1z1為慣性坐標系，Oxyz為衛星本體坐標系，Ofxfyfzf為天線結構坐標系，O為天線結構未發生變形時整星的質心，lpf為天線結構局部坐標系原點Of在衛星本體坐標系下的位置矢量。系統中（包括剛體）任一質量元mk，如果mk是天線結構上的質量元，則uk指的是mk在天線結構局部坐標系Ofxfyfzf中的位移；如果mk是衛星剛體上的質量元，則uk＝0。質量元mk在慣性坐標系O1x1y1z1中的線速度為

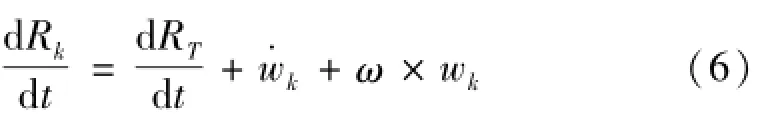
其中：Rk，RT，wk的物理意義見圖1，ω為衛星的絕對角速度。

圖1 衛星－撓性附件系統示意圖Fig.1 Satellite-flexible appendage system

假定天線結構的變形為小變形，變形后的位移函數為一階小量，并做部分線性化處理［15］，可得wk＝lpf＋rk＋uk，l·

pf＝0，r·k＝0，RT＝0，略去二階以上小量，式（6）變為

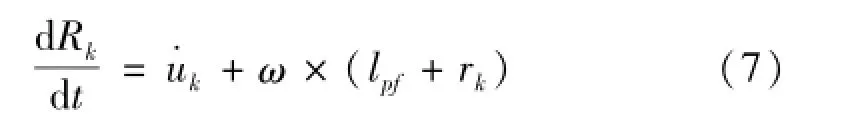
設系統相對于O點的絕對角動量為H，系統受到的相對于O點的外力矩為Msat，根據角動量定律，有

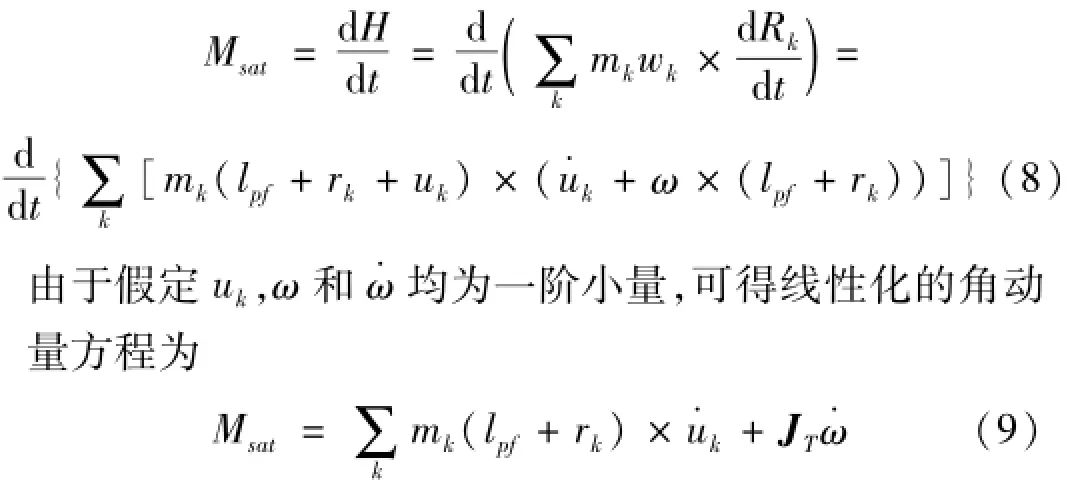
其中：JT為未變形時整星的慣量矩陣。

對天線結構進行有限元模態分析，可以得到天線在天線結構局部坐標系中的結構振型為Φk＝［φ1（rk），φ2（rk），…，φn（rk）］，k＝1，2，…，N，n為截取模態數，N為天線結構的節點數；固有頻率為ω1，…，ωn。在坐標系Ofxfyfzf中，由振型疊加法，uk（t）＝Φkq（t），這里q（t）＝［q1（t），q2（t），…，qn（t）］T，q（t）是天線結構的有限元離散模態坐標。

在數學上，矢量r＝［rxryrz］T，b＝［bxbybz］T，其叉乘r×b可以表示成矩陣與矢量相乘的形式

可以看出，Brot為天線結構對于本體坐標系Oxyz的轉動耦合系數。

2.2 撓性天線的運動方程

3 仿真算例

3.1 模型描述

本文對圖2所示的衛星－天線系統進行熱致耦合動力學分析。其中，衛星作為中心剛體，其質量為1100 kg；環形可展開天線與伸展臂結構作為衛星的撓性附件，天線結構部分質量84.36 kg；整星在坐標系Oxyz中的轉動慣量分別為Jx＝5 729.2 kgm2，Jy＝4 583.3 kgm2，Jz＝2 979.2 kgm2，衛星姿態控制參數取值為K1＝－10 Nm/rad，K2＝－100 Nm/rad；天線的口徑為20 m，伸展臂長度為9.5 m，天線的周邊桁架材料為碳纖維，索網材料為尼龍，金屬反射網材料為鍍金鉬絲，各種材料的熱參數和結構參數見表1；天線結構各階模態的阻尼比都取0.05。

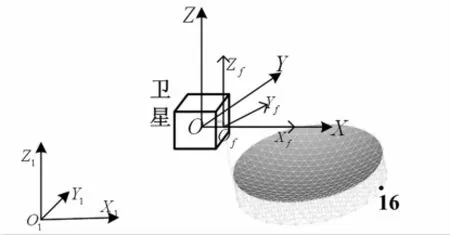
圖2 衛星－天線系統示意圖Fig.2 Satellite-antenna system

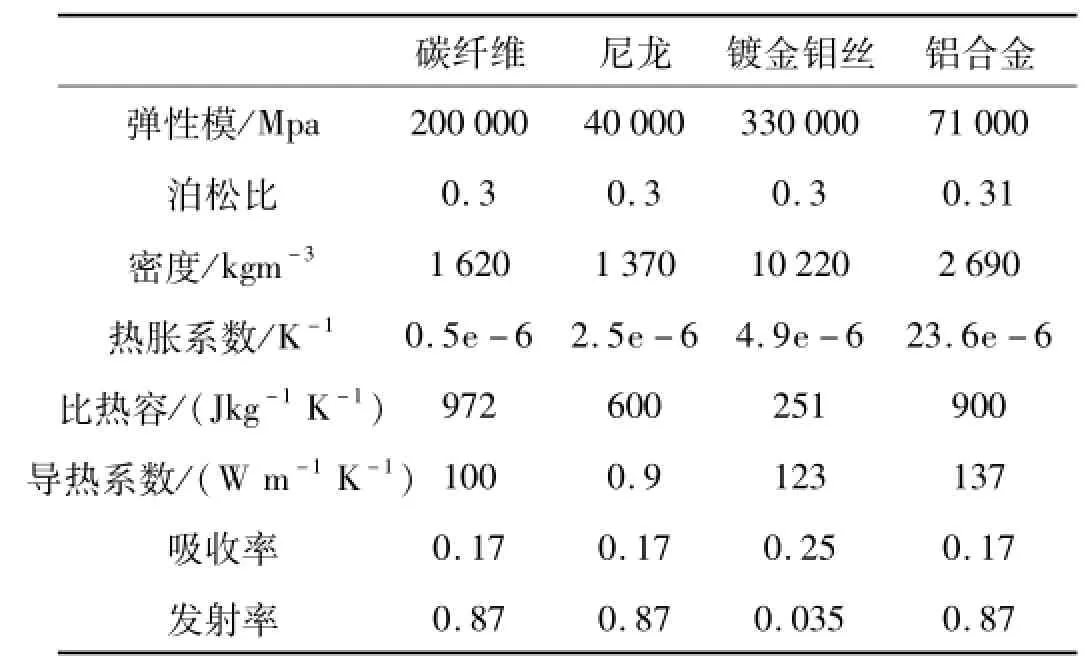
表1 材料參數表Tab.1 Thematerial parameter table

3.2 進出陰影溫度場分析

3.2.1 計算工況

本算例中，衛星－天線在地球同步軌道上運行，太陽位置處于春分點，這里重點分析天線進出地球陰影區前后的溫度場變化規律。天線在軌進出陰影的過程如圖3所示，位置A表示天線進入陰影區，B表示天線處于陰影區，C表示天線離開陰影區。天線的尺寸相對軌道來說很小，所以忽略進入（離開）陰影區的時間，認為進、出陰影時熱流發生突變。

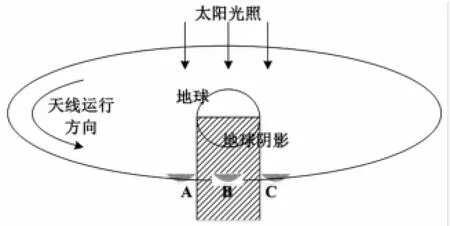
圖3 天線進出陰影區示意圖Fig.3 Antenna entering and leaving the Earth’s shadow

3.2.2 溫度場計算結果與分析

太陽位置處于春分點時，地球同步軌道的陰影區總時間為4 140 s，這里從天線進入陰影區前1 000 s開始計算，計算的總時間為7 200 s。本文采用有限元方法對天線結構進行瞬態溫度場求解，計算結果如圖4、5所示。圖4顯示了天線典型節點（圖2所示節點16）進出陰影區的溫度變化，圖5進出陰影過程中天線的最高、最低、平均溫度的變化情況，“天線的平均溫度”是通過天線結構所有節點的溫度取平均值得到的，可以看出，在1 000 s時刻天線進入陰影區，之后天線溫度逐漸降低，在5 140 s時刻天線出陰影，出陰影后經過十幾分鐘時間天線溫度達到穩定狀態，天線出陰影比進陰影的溫度變化更劇烈。所以，在后續的振動分析時，重點分析出陰影時的熱致耦合動力學響應。

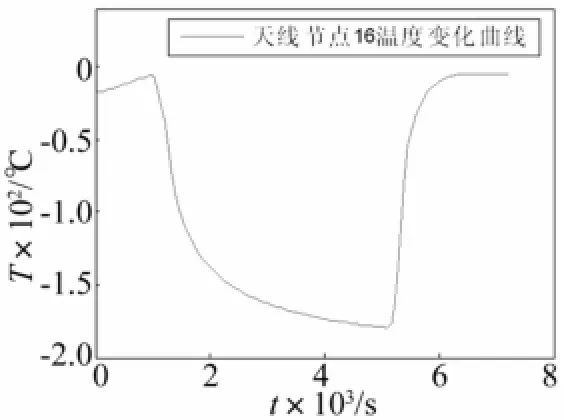
圖4 天線節點16溫度曲線Fig.4 Temperature curve of antenna’s node16

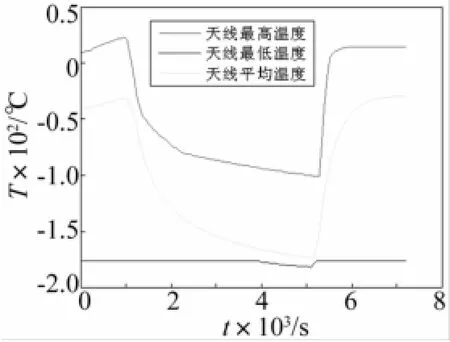
圖5 天線的最高、最低、平均溫度變化曲線Fig.5 Change curves of antenna’smax，min and average temperature

圖6 天線結構簡單分區Fig.6 Simple partition of antenna

為了進一步揭示天線出陰影時的溫度變化規律，將天線結構進行簡單的分區，如圖6所示，記虛線a－a之上為天線的迎光側，a－a之下為天線的背光側，b－b之左為天線左半側，b－b之右為天線右半側。分別求出天線結構迎光側、背光側、左半側和右半側的平均溫度，這里的“平均溫度”指的是結構對應部分的所有節點溫度取平均值，其變化曲線如圖7、8所示，可以看出，天線在進、出陰影的過程中，天線結構自身的溫度場是不均勻的，而且不均勻性主要表現為迎光側和背光側之間存在較大的溫差，所以，天線出陰影過程中自身的熱傳導主要發生在是迎光側與背光側之間。

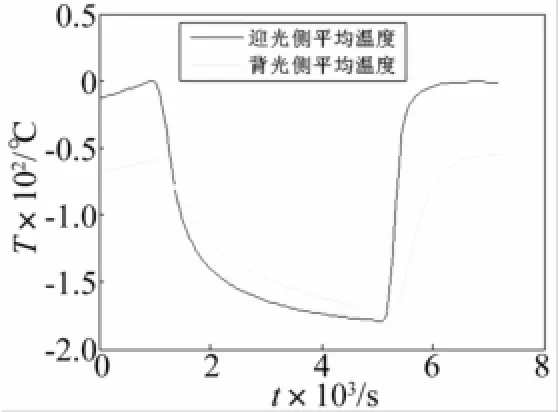
圖7 天線迎光側、背光側平均溫度Fig.7 Temperature curves of antenna’s light side and backlight side

下面對迎光側與背光側之間熱傳導的熱響應特征時間進行估算。首先，采用形如T（t）＝T0＋TS（1－e（t－t1）/τ）的函數［9］，分別對出陰影過程中天線迎光側平均溫度和背光側平均溫度進行曲線擬合，可求得，迎光側溫變曲線為T1（t）＝－180＋180（1－e（t－5140）/282），背光側的溫變曲線為T2（t）＝－175＋130（1－e（t－5140）/335），可以估算出，熱響應特征時間tT約為280 s～330 s。

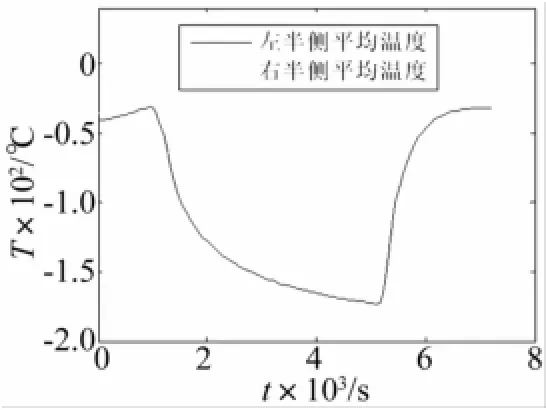
圖8 天線左側、右側平均溫度Fig.8 Temperature curves of antenna’s left side and right side

3.3 耦合動力學分析

3.3.1 天線結構模態分析

對于天線結構部分，如圖2所示，在天線大臂與衛星的連接處（點Of處）施加固定約束，并對天線結構采用有限元方法進行模態分析，分析結果如圖9所示，其中第一排從左至右為第1、2、3階振型，第二排為第4、5、6階振型，第三排為第7、8、9階振型。為方便地描述各階振型，可以將天線與伸展臂整體結構看成是兩部分子結構的組合。

圖9 天線前9階振型Fig.9 First to ninth order vibration mode of antenna

表2列出了天線結構前9階振型所對應的固有頻率值，可以看出，天線的前幾階固有頻率很低且相接近，天線結構具有大柔性的特點。

表2 天線結構前9階固有振動特性Tab.2 First to ninth order natural vibration characteristic of antenna

3.3.2 熱致耦合動力學響應結果與分析

對圖2所示的衛星天線耦合系統，將3.2節求得的天線結構出陰影的溫度場采用有限元法轉化為節點載荷，形成天線的載荷矩陣Q（t），即可采用式（18）的剛柔耦合動力學方程進行熱致耦合動力學求解。

計算的結果如圖10、11所示。圖10為天線節點16的位移曲線（節點16的位置見圖2），天線X方向最大靜位移為1.90 mm，天線X方向最大振幅為0.08 mm，天線Y方向最大靜位移為0.56 mm，天線Y方向最大振幅為0.02 mm，天線Z方向最大靜位移為4.11 mm，天線Z方向最大振幅為0.25 mm，可以看出，天線的熱靜變形和熱致振動主要體現在Z方向上，動態成分約占總位移的5%，這與3.2.2節中溫度梯度主要存在于迎光側和背光側的規律是一致的。圖11為天線出陰影過程中衛星姿態角變化曲線，可以看出，對于圖2所示的分析模型，變化的熱載荷主要導致衛星繞自身Y軸做低頻振蕩運動，繞Y軸的姿態角振蕩幅度為1.6 ×10－3度。

圖10 天線節點16位移曲線Fig.10 Displacement curve of antenna’s node 16

圖11 衛星姿態角變化曲線Fig.11 Change curves of satellite attitude angles

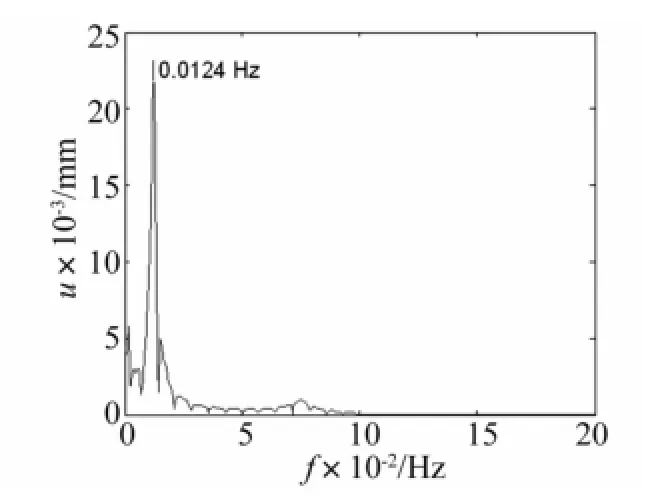
圖12 節點16X向位移頻譜分析Fig.12 Spectrum analysis of node 16 X direction displacement

對天線節點16的位移進行頻譜分析，X向、Y向、Z向位移的頻譜曲線如圖12～14所示，X向位移的頻譜響應為0.012 4 Hz，Y向位移的頻譜響應為0.013 5 Hz，Z向位移的頻譜響應為0.012 4 Hz，基本上與天線結構的第一階和第二階模態相吻合，這說明出陰影時的熱載荷主要激起了天線的前兩階模態。

熱致耦合動力學響應所導致的天線形面精度均方根誤差（RMS）的變化情況如圖15所示，在出陰影的過程中，動態RMS的最大振幅為0.1 mm，與準靜態相比，增大了3.7%。

根據上述結果與分析，熱載荷引起的振動響應雖然不是影響天線形面精度的主要因素，但是已經不容忽視。在本算例中，天線結構的熱特征時間tT約為280 s～330 s，而結構響應特征時間tS為84.75 s，tT約為tS的4倍。

隨著航天技術發展，可展開天線呈現口徑越來越大、柔性越來越大的趨勢，tT與tS也呈現越來越接近的趨勢。現將溫度載荷變化速度加快一倍，將結構的彈性模量減小為原來的四分之一，則tT與tS非常接近。

采用本文的方法，重新進行熱致耦合動力學分析，結果如圖16～18所示。由圖16，天線的熱致靜變形和熱致振動仍主要體現在Z方向上，節點16的Z向最大靜位移仍為4.11 mm，Z向最大振幅為0.98 mm，動態成分占到總位移的19.3%。由圖17，衛星繞Y軸的姿態角振蕩幅度達到了4.8×10－3度。由圖18，動態RMS的最大振幅為0.45 mm，與準靜態相比，增大了16.7%。綜上可知，當tT與tS非常接近時，熱載荷會導致結構發生非常劇烈的振動響應，采用本文的方法可以對大型復雜空間結構的熱致耦合動力學響應進行合理的預測。

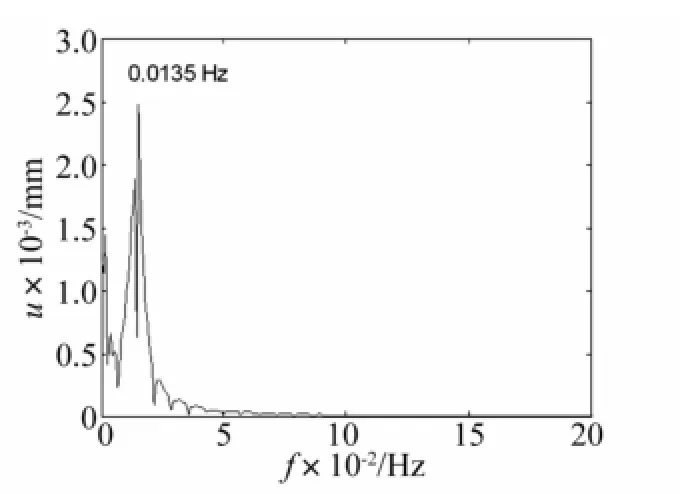
圖13 節點16Y向位移頻譜分析Fig.13 Spectrum analysis of node 16 Y direction displacement

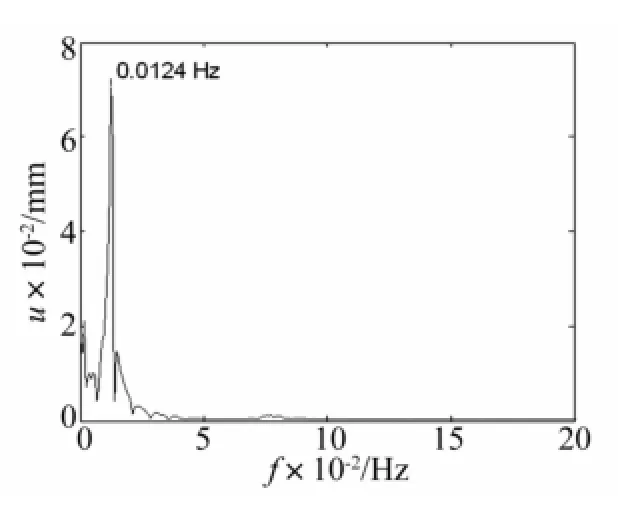
圖14 節點16Z向位移頻譜分析Fig.14 Spectrum analysis of node 16 Z direction disp lacement

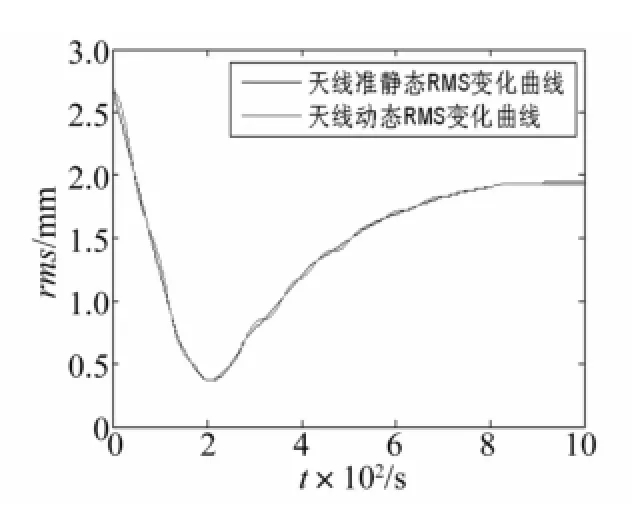
圖15 天線形面精度變化情況Fig.15 Change curve of antenna’s RMS

圖16 改變參數后天線節點16位移曲線Fig.16 Displacement curve of antenna’s node 16 with parameters changed

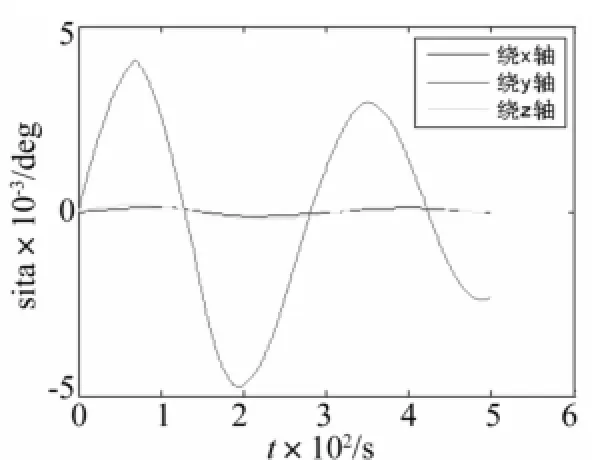
圖17 改變參數后衛星姿態角變化曲線Fig.17 Change curves of satellite attitude angleswith parameters changed

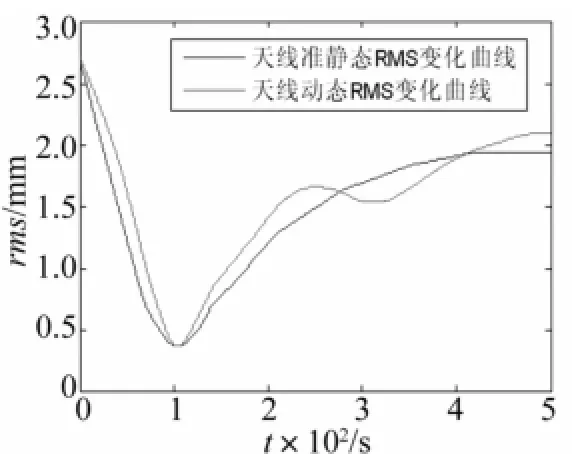
圖18 改變參數后天線形面精度變化情況Fig.18 Change curve of antenna’s RMSwith parameters changed

4 結 論

（1）大型可展開進出陰影的過程中，其自身溫度梯度主要體現在迎光側與背光側之間，熱傳導也主要發生在這里，可以采用本文的方法估測熱響應特征時間tT。

（2）仍可采用Boley理論，通過tT與tS對天線進出陰影區時的熱致耦合動力學響應進行預測。

隨著航天技術發展，可展開天線的口徑越來越大，天線的柔性也會越來越大，熱響應時間常數和結構響應常數呈現越來越接近的趨勢，進出陰影的熱致耦合動力學問題必將成為星載天線設計中必須考慮的重要問題之一，本文的方法對今后的工程實際具有很重要的指導意義。

［1］Foster C L.Solar array induced disturbance of the hubble space telescope pointing system［J］.Journal of Spacecraft and Rocket，1995，32（4）：634－644.

［2］Thornton E A.Thermal structures for aerospace applications［M］.In：AIAA Education Series.Virginia：AIAA Inc.，1996：343－397.

［3］張宗美.航天故障手冊［M］.北京：宇航出版社，1994.

［4］Boley B A.Thermally induced vibrations of beams［J］.Journal of the Aeronautical Science，1956，23（2）：179－181.

［5］Boley B A，Weiner J H.Theory of thermal stresses［M］.John Wiley and Sons，1960：339－345.

［6］Thornton E A，Kim Y A.Thermally induced bending vibrations of a flexible rolled-up solar array［J］.Journal of Spacecraftand Rocket，1993，30（4）：438－448.

［7］Li Wang，Xiang Z H，Chen L J，et al.Thermal flutter analysis of large-scale space structures based on finite element method［J］.International Journal for Numerical Methods in Engineering，2007，69（5）：887－907.

［8］Xue MD，Duan J，Xiang Z H.Thermally-induced bendingtorsion coup ling vibration of large scale space structures［J］.Computational Mechanics，2007，40（4）：707－723.

［9］Johnston J D，Thornton E A.Thermally induced attitude synamics of a spacecraft with a flexible appendage［J］.Journal of Guidance Control and Dynamics，1998，21（4）：581－587.

［10］Shen Z X，Tian Q，Liu X N，et al.Thermally induced vibrations of flexible beams using Absolute Nodal Coordinate Formulation［J］.Aerospace Science and Technology，2013， 29（2013）：386－393.

［11］安翔，馮剛.某空間站太陽電池陣中央桁架熱－結構耦合動力學分析［J］.強度與環境，2005，32（3）：8－14.

AN Xiang，FENG Gang.Thermally induced vibration of the mainmast of the space station’s solar arrays［J］.Structure and Environment engineering，2005，32（3）：8－14.

［12］楊玉龍，關富玲.展開桁架天線熱致振動數值分析［J］.空間科學學報，2009，29（4）：432－437.

YANG Yu-long，GUAN Fu-ling.Numerical analysis of thermally induced vibration for deployable truss antenna［J］.Chin.J.Space Sci.，2009，29（4）：432－437.

［13］劉勁，朱敏波，曹罡.星載可展開天線熱振動數值分析［J］.中國空間科學技術，2011，31（2）：53－57.

LIU Jin，ZHU Min-bo，CAO Gang.Numerical analysis of thermally induced vibration for deployable antenna［J］.Chinese Space Science and Technology，2011，31（2）：53－57.

［14］張洪武，關振群，李云鵬，等.有限元分析與CAE技術基礎［M］.北京：清華大學出版社，2004.

［15］葛升民，王磊，甘克力，等.星載大型空間天線的一種解耦控制方法［J］.宇航學報，2013，34（1）：46－53.

GE Sheng-min，WANG Lei，GAN Ke-li，et al.A method for decoupling control of satellite-borne large space antenna［J］.Journal of Astronautics，2013，34（1）：46－53.

Thermal induced coup ling-dynamic analysis of a dep loyable satellite antenna system

YANGGui-geng，ZHU Min-bo，LIAN Pei-yuan，GAO Feng，ZONG Ya-li
（MOE Key Laboratory of Electronic Equipment Structure Design，Xidian University，Xi'an 710071，China）

The coupling-vibration of a spacecraft with a large ring-shaped deployable antenna induced by temperature variations during the spacecraft entering and leaving the Earth's shadow was numercially analyzed.The transient temperature field of the large deployable antennawas solved using the finite elementmethod，and a rigid-flexible coupling dynamic modelwas established for the coupling-vibration analysis of a deployable satellite antenna system.The results showed that temperature gradient of the antenna itself existsmainly between the light side and the backlight side，and with it the thermal response characteristic time of antenna was estimated.The obvious thermal induced couplingvibration of the antenna structure and the satellite attitude could be observed.Themethod presented here could be used to reasonably predict the thermal induced coupling-dynamic responses of a deployable satellite antenna system.

deployable antenna；thermal response characteristic time；satellite-antenna rigid-flexible coupling；thermal induced coupling-dynamics

V414

A

10.13465/j.cnki.jvs.2014.24.029

國家自然科學基金（51035006，51205301）

2013－10－21 修改稿收到日期：2013－12－24

楊癸庚男，博士生，1989年4月生