Alpha穩定分布序列的數值仿真方法

彭 成，王平波，劉旺鎖

(海軍工程大學，湖北武漢 430033)

0 引 言

水聲混響信號的統計特性表明，它具有顯著的尖峰脈沖特性和厚拖尾現象。這與機載雷達的地面散射干擾非常相似。因此主動聲吶抗混響可以借鑒Alpha穩定(Sα)分布在雷達雜波抑制[1]中的應用方法[2]。

Alpha穩定分布[3]又稱為非高斯穩定分布，最初由利維(Levy)于1925年提出。但直到1993年，Shao和 Nikias的論文[4]才將對稱 Alpha穩定分布(S Sα分布，一類Sα分布特例)模型應用于描述具有尖峰沖激、厚拖尾的噪聲。目前大多數信號處理的研究都假設噪聲或干擾是服從高斯分布[5,6]。然而實際干擾的統計特性并不總是符合高斯假設的，它們常具有顯著的尖峰，如雷達地面散射干擾、主動聲吶混響干擾、音頻信號噪聲、遠程電話噪聲等。對于這些干擾信號，基于高斯假設顯然是不恰當的。而Sα分布模型，能取得較好的處理效果。

目前信號處理中都使用標準參數系表征Sα分布。因此本文從Sα分布模型的定義和性質出發，討論了易混淆的三種參數系的關系，進而實現了標準參數系下Sα分布隨機變量的產生。通過該方法產生不同參數組合的隨機序列，并將對應的概率密度函數(Probability Density Function, PDF)與理論對PDF進行對比分析，驗證Sα分布隨機變量產生方法的正確性。

1 Alpha穩定分布的定義及性質

αS分布是廣義的高斯分布，它比高斯分布具有更廣泛的適用性。通常通過特征函數來給出αS分布的定義。αS分布具有三種不同的參數系[7]表征方法，即標準參數系S、S1參數系和S2參數系。而標準參數系下的定義是最常用的。

定義 1[3]：如果隨機變量X存在參數0 ＜α≤2,γ≥ 0 ,?1 ≤β≤1和實數μ使其特征函數如式(1)所示?(t)=

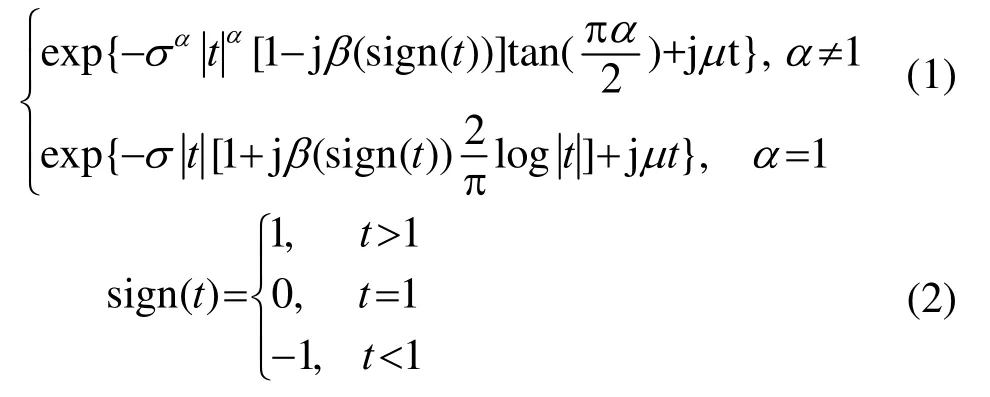
則稱隨機變量X服從S參數系下的αS分布。式(1)中，參數α稱為特征指數，決定分布脈沖特性的程度；β稱為對稱參數，用它來確定分布的斜度；σ稱為分散系數，它是分散程度的度量；參數μ稱為位置參數。然而在標準參數系下，當α=1，β≠0時，其特征函數在隨機變量的取值上均不連續。

定義 2[3]：S1參數系的產生是為了消除S參數系特征函數的不連續性，其特征函數如式(3)所示?(t)=

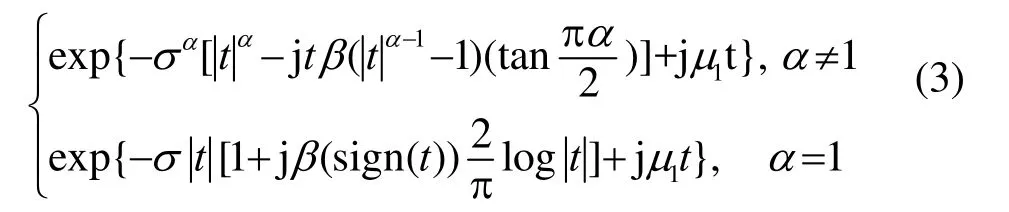
其中μ1與S參數系的μ具有如下式的關系

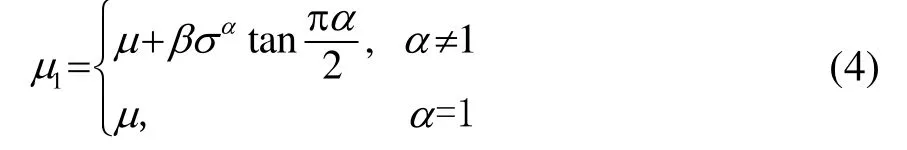
這個特征函數在α、β的所有值均聯合連續，但有一點不足是其μ1不再具有位置參數原有的意義，而其他三個參數與S參數系下對應參數相同。

定義 3[3]：S2參數系主要是利于理論分析和推導，其特征函數具有如式(5)所示的形式?(t)=

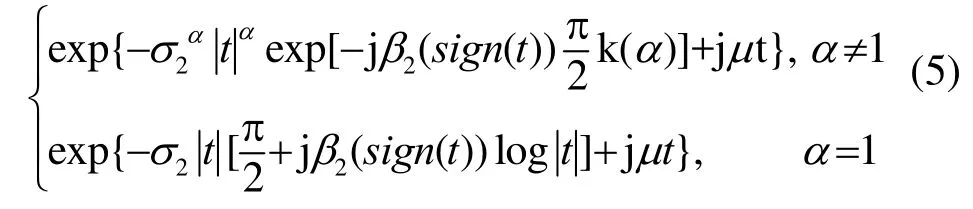
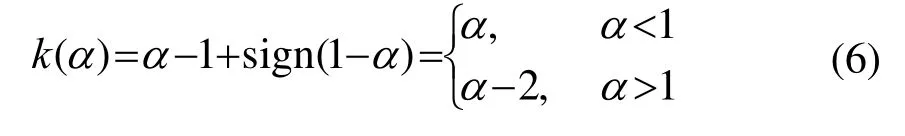
其中參數α和μ與標準參數系的對應參數相同，參數β2和σ2與標準參數系下的參數變換關系如下：

當1≠α時

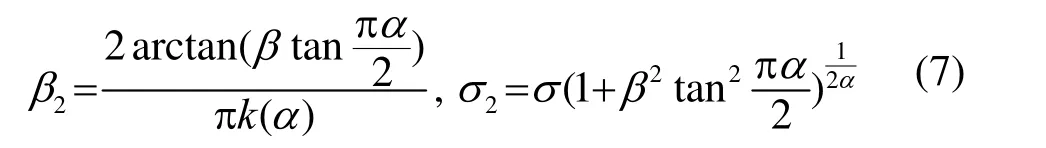
當1=α時

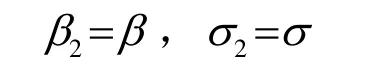
特征函數是研究αS分布的一個有用工具，利用它可以得出穩定分布的很多性質，下面只給出本文需要的兩個基本性質：

性質1：若X～S(α,σ,β,μ)，a是一個實常數，則

性質2：若X～S(α,σ,β,μ)，b是一個非零的實常數，則

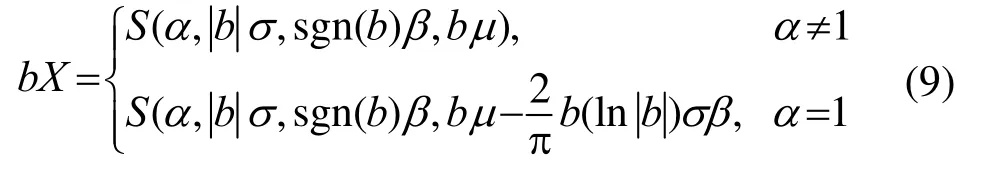
2 Alpha穩定分布的產生方法

S1參數系的作用是為了消除S參數系在α=1,β≠ 0 時的不連續性；而S2參數系的主要作用是便于理論推導和分析。因此通過S1、S2參數系與S參數系間的轉換關系，就能產生出S參數系下符合αS分布的隨機變量及畫出PDF圖。

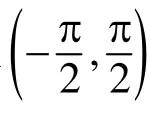
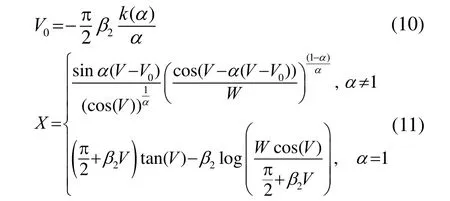
(2) 然后再根據S和S2兩個參數系間的轉換關系，推導出標準參數系下服從S(α,β, 1, 0)分布的隨機變量Y的生成方法。

當α≠1時，首先定義

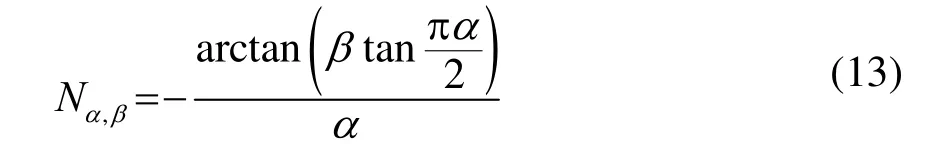
其中Mα,β代表了參數σ2與σ間的變換關系；Nα,β代表了參數β2與β間的變換關系，用以替代S2參數系產生方法中的V0。于是Y=

當α=1時，M =π/2，β2=β ，有

生成的Y即為標準參數系下服從Y～S(α,β,1,0)分布的隨機變量。

(3) 再利用αS分布的兩個基本性質，可得

這里，隨機變量Z即滿足Z～S(α,β,σ,μ)。

如此即產生了標準參數系下滿足四個參數規定范圍內的、服從任意參數值組合的αS分布隨機變量。

3 Alpha穩定分布序列的生成

由于Sα分布的特征函數與概率密度函數具有如下的對應關系：

而S參數系下特征函數在α=1、β≠0時不連續，因此采用直接數值積分法[8]來計算概率密度函數值。首先對S1參數系下的特征函數進行數值積分，克服S參數系下的不連續性，然后利用S參數系與S1參數系下參數間的變換關系及αS分布的兩個基本性質，即可計算出S參數系下的概率密度函數值。

通過運用上述αS分布隨機變量生成方法，分別產生三組不同參數組合的 1000點穩定分布隨機變量序列。同時利用產生的隨機變量序列通過直接數值積分法計算出概率密度函數值，并與統計PDF進行性能分析比較，如圖1~3所示。

圖1 S(1.8,0,1,0)分布序列及PDFFig.1 The sequence and PDF of S(1.8,0,1,0)

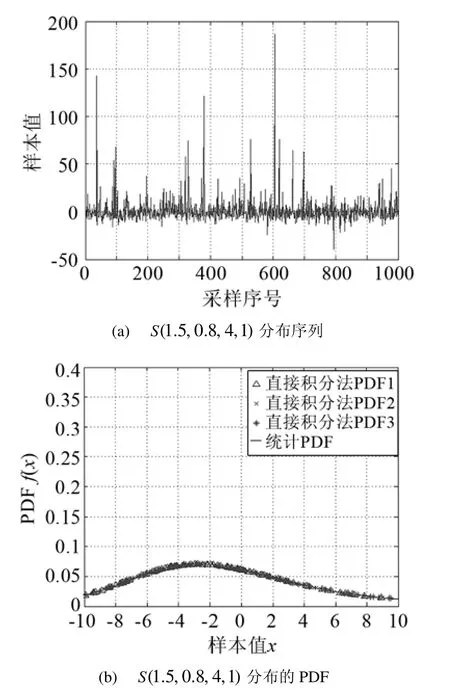
圖2 S(1.5,0.8,4,1)分布序列及PDFFig.2 The sequence and PDF of S(1.5,0.8,4,1)

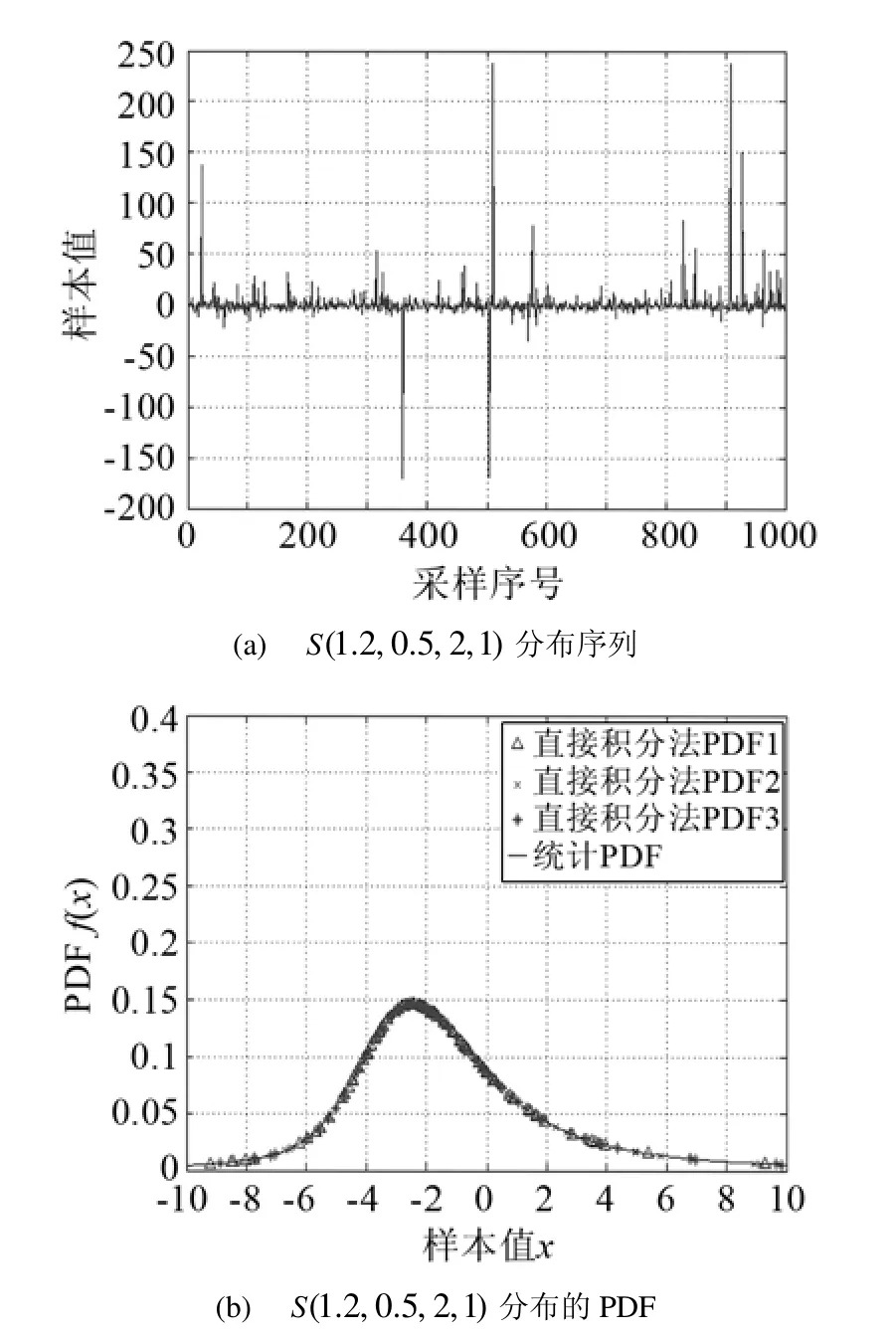
圖3 S(1.2,0.5,2,1)分布序列及PDFFig.3 The sequence and PDF of S(1.2,0.5,2,1)

由圖1(a)~3(a)可以看出，αS分布隨機變量隨著特征指數α的減小，其尖峰脈沖性越顯著。而由圖1(b)~3(b)可知，本文方法產生的隨機變量序列通過直接積分法得到的PDF與Sα分布的統計PDF擬合性能很好，驗證了本方法的正確性。

圖4 Sα(0,1,0)分布的PDF拖尾Fig.4 The PDF tails of Sα(0,1,0)

圖4繪出了不同α取值下的Sα分布PDF拖尾比較，可進一步演示驗證Sα分布的特性：α取值越小，其拖尾越厚，說明大樣本發生概率越高，非高斯脈沖性越強；反之，α取值越大，其拖尾越薄，說明大樣本發生概率越低，非高斯脈沖性越弱。

4 結束語

本文詳細介紹了如何在標準參數系下產生αS分布隨機變量的方法，即利用S1、S2參數系與S參數系參數間的轉換關系來產生隨機變量，克服了S系不便于理論分析和推導的缺點。

通過產生三組不同參數組合的Sα分布隨機變量序列，對產生的序列直接積分求PDF并與Sα分布的統計PDF進行性能比較，結果擬合非常好，驗證了產生方法的正確性和有效性。本文的隨機變量產生方法能產生S Sα分布隨機變量，這為后續主動聲吶抗混響信號處理研究能提供準確的仿真數據基礎，是值得深入研究的。

參考文獻

[1] 呂曉蕊. Alpha穩定分布的模型仿真及參數估計[D]. 武漢: 華中科技大學, 2008.Lü Xiaorui. Modeling simulation and parameter estimation of alpha stable distribution[D]. Wuhan: Huzhong University of Science and Technology, 2008.

[2] 王汗青. 基于對稱 Alpha穩定分布的水聲信號處理技術研究[D].武漢: 海軍工程大學, 2012.WANG Hanqing. Study on underwater acoustic signals processing based on symmetrical alpha stable distribution[D]. Wuhan: Naval University of Engineering, 2012.

[3] 邱天爽, 張旭秀, 李小兵, 等. 統計信號處理: 非高斯信號處理及其應用[M]. 北京: 電子工業出版社, 2004.QIU Tianshuang, ZHANG Xuxiu, LI Xiaobing, et al. Statistical signal processing: non-gaussian signal processing and its application[M]. Beijing: Electronic Industry Press, 2004.

[4] Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010.

[5] 朱埜. 主動聲吶檢測信息原理[M]. 北京: 海洋出版社, 1990.ZHU Ye. Information principles of active sonar signal detection[M]. Beijing: Ocean Press, 1990.

[6] Whalen A D. Detection of signals in noise[M]. New York: Academic Press, 1971.

[7] Rafal Weron. On the Chambers-Mallows-S-tuck method for simulating skewed stable random variables[J]. Statistics & Probability Letters, 1996, 28(2): 165-171.

[8] Nolan J P. An algorithm for evaluating stable densities in zolotarev’s parameterization[J]. Mathematical and Computer Modelling,1999, 29(3): 229-235.