雙足驅動雙壓電晶片直線超聲波電機運行機理研究

陳 強，徐志科，蔣春容，陸旦宏

（1．南京工程學院電力工程學院，南京 211167；2．東南大學電氣工程學院，南京 210096）

雙足驅動雙壓電晶片直線超聲波電機運行機理研究

陳 強1，徐志科2，蔣春容1，陸旦宏1

（1．南京工程學院電力工程學院，南京 211167；2．東南大學電氣工程學院，南京 210096）

研究新型直線超聲波電機運行機理，采用雙壓電晶片及雙足驅動結構，具有結構簡單、無需頻率簡并、易于小型化等優點。詳述其結構、振形特點及工作機理。建立電機定子振動響應有限元模型，給出輸入阻抗計算方法。用已建模型計算獲得定子驅動足接觸點在諧振頻率點附近振幅，推導驅動足接觸點運動軌跡。通過實測定子阻抗特性將所得結果與理論分析進行比較。

直線超聲波電機；雙壓電晶片；雙足驅動；有限元模型；運動軌跡；阻抗特性

超聲波電機利用壓電陶瓷逆壓電效應激勵定子產生超聲振動，將電能轉化為機械能通過定子與動子間摩擦耦合方式驅動。與傳統電磁電機相比，超聲波電機具有低速大轉矩、響應速度快、斷電自鎖、結構簡單、噪音小、不受電磁場干擾等優點［1］。作為控制系統的執行元件在工業控制系統、半導體工業、精密儀器、航空航天、醫療、機器人等高新技術領域具有廣闊的應用前景［2－3］。直線超聲波電機為超聲波電機重要分支，除以上述優點外亦具有無需絲桿機構運動轉換直接輸出牽引力、定位及速度控制精度高、結構簡單、設計靈活等優點，作為重要控制系統執行元件在微機電系統中廣泛應用［4－6］。

本文電機采用雙壓電晶片與雙足驅動結構［7］。該電機結構簡單體積小，易于裝配各種裝置；無需頻率簡并，設計較靈活，可進一步小型化。且雙足驅動能使定子在一個工作周期內兩次推動動子作直線運動，從而提高電機的輸出力及工作效率。

1 電機結構與原理

1.1 電機結構

圖1為雙足驅動雙壓電晶片直線超聲波電機結構，由1定子、2動子、3導軌、4底座及5預壓機構組成。在動、定子驅動足接觸區內將摩擦材料貼于動子面［8］。

圖2為定子結構及壓電陶瓷極化方向，由兩組壓電陶瓷片（A、B組）及彈性體組成，定子兩端固定。兩組陶瓷片與彈性體粘結部分接地，另一面接激勵電源，激勵電源頻率相同相位相差90°，為使定子驅動足獲得盡可能大振幅以提高電機工作效率，電源工作頻率盡量接近諧振頻率［9］。定子結構尺寸見表1，定子彈性體采用青銅，壓電材料為PZT8。

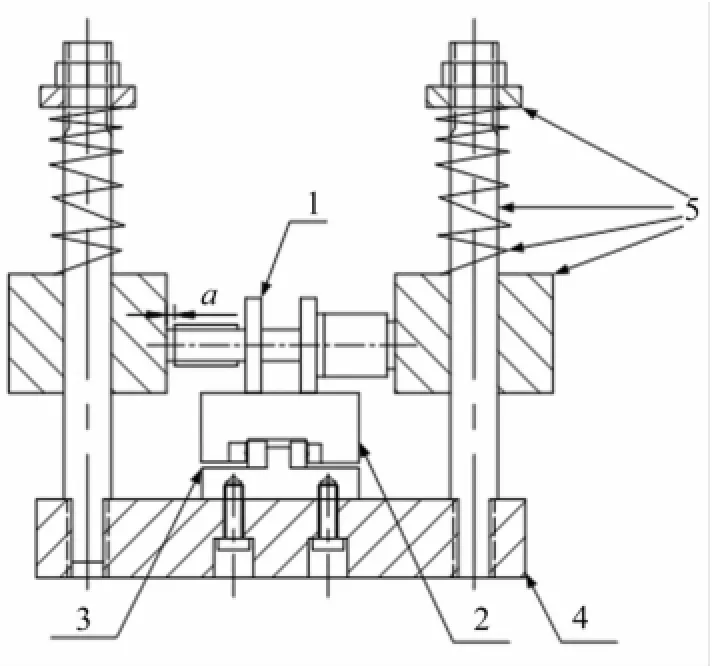
圖1 雙足驅動雙壓電晶片直線超聲波電機結構Fig．1 Configuration of double-driving feet linear ultrasonic motor using bimorphs

圖2 定子結構及壓電陶瓷極化方向Fig．2 Structure of stator and polarization direction of piezoelectric ceramics

表1 定子結構尺寸參數Tab.1 Value of the stator structure parameter

1.2 定子振動模態與工作原理

定子工作模態由兩正交二階彎曲振動復合而成。用有限元軟件ANSYS計算定子振動模態［10－12］，所得振動模態見圖3，共振頻率為28187 Hz。對兩組陶瓷片分別施加90°相差的激勵電源，兩組陶瓷片共同作用，兩驅動足交替驅動動子運動。

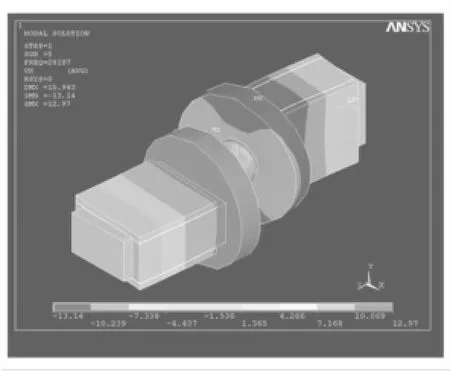
圖3 定子振動模態Fig．3 Vibration modes of stator

A組陶瓷片施加的激勵電源相位較B組超前90°，動子沿X負向運動，電機定子、動子接觸過程及其在一周期內4個相互位置及受力見圖4。對兩組壓電陶瓷施加激勵電壓時，會激起驅動足接觸點X、Y、Z向振幅。由于Z向振幅不影響動子運動方向暫不考慮，將在運動軌跡中分析。通過交換兩激勵電源相序即可使動子反方向運動。

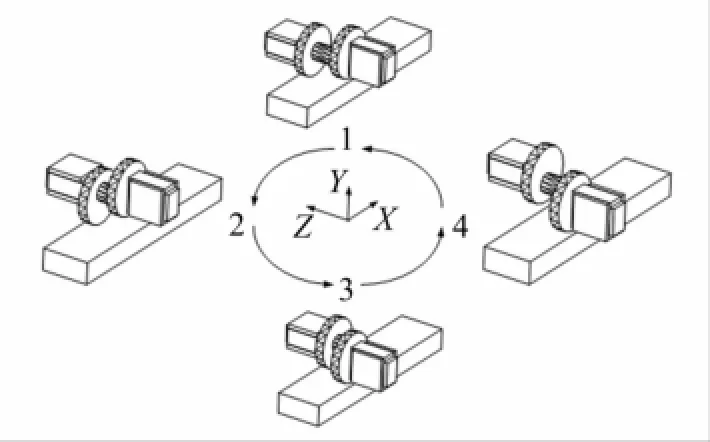
圖4 電機工作原理示意圖Fig．4 Schematic diagram of themotor’s work principle

（1）A組壓電陶瓷施加激勵電壓相角ωt＝0時，驅動足A在X正向振幅達最大，驅動足B在X負向振幅達最大，此時驅動足A、B均不驅動動子。

（2）ωt＝π／2時驅動足A在Y負向振幅達最大，驅動足B在Y正向振幅達最大；此時驅動足A與動子接觸，具有X負向振動速度，推動動子沿X負向運動，驅動足B與動子不接觸。

（3）ωt＝π時驅動足A在X負向振幅達最大，驅動足B在X正向振幅達最大，此時驅動足A、B均不驅動動子。

（4）ωt＝3π／2時驅動足A在Y正向振幅達最大；驅動足B在X方向位移為，驅動足B在Y負向振幅達最大，此時驅動足B與動子接觸，具有X負向振動速度，推動動子沿X負向運動，驅動足A與動子不接觸。

2 定子模型分析

超聲波電機工作機理主要體現于兩機電能量的傳遞過程［13－14］，即對定子振型、壓電陶瓷極化與配置設計，由驅動控制電路使定子產生機電耦合振動；通過摩擦耦合將定子的機械能轉為轉子動能輸出。在第一能量傳遞過程中利用諧振方式進行能量轉換，電機驅動器功放部分普遍采用兩相同推挽放大器，要求對電機及驅動器中變壓器間阻抗匹配，本文利用有限元法對電機輸入阻抗進行定量分析，并計算諧振頻率點附近振幅。

2.1 模型建立

由于兩組壓電陶瓷能量轉換模式d33方向相互垂直，定義局部坐標系X′Y′Z′及X″Y″Z″（圖2），分別在兩坐標系下定義A、B組壓電陶瓷性質。定子兩端固支，計算時設電機定子環的壓電陶瓷對各自坐標系同方向極化，在施加電壓載荷時可參照圖2極化方向施加電壓。因本文兩邊正交對稱，因此只分析A組壓電陶瓷振動響應模型。利用有限元分析軟件ANSYS對電機定子進行分析，模型采用4節點3維實體耦合單元Solid98剖分電機定子，計算時需考慮電機定子結構載荷與電載荷。

2.2 輸入阻抗計算

模型中電位移矢量Φ的頻率變化范圍為20～40 kHz，通過計算可得電機模型節點電荷值。電機電極電流［15］可表示為

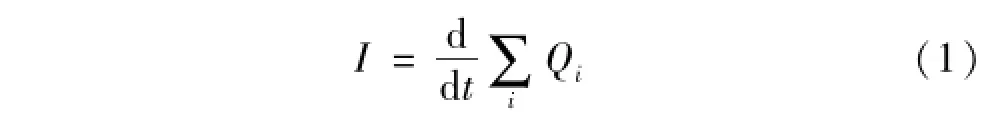
式中：Qi為電機電極節點電荷；∑iQi為電機電極電荷總和。

由于激勵電壓為正弦規律，可認為電極電荷符合正弦規律，可表示為

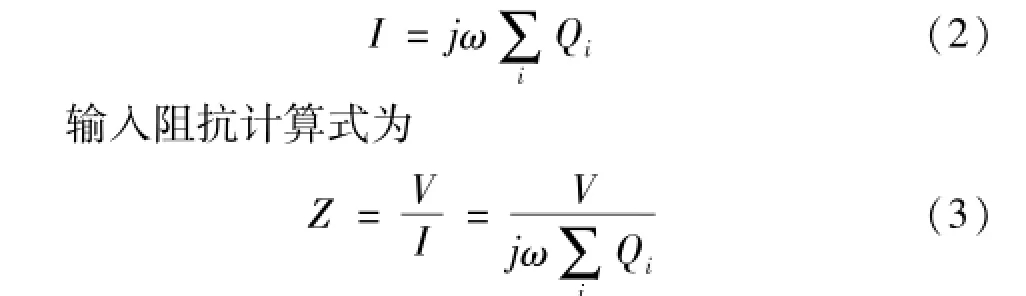
在20～40 kHz頻率范圍內選1 000點進行計算，通過以上方法可得定子阻抗－頻率特性，見圖5。由圖5看出，阻抗值在頻率28 200 Hz時由局部最小值躍至局部最大值，該最小值對應頻率位于電機定子振動諧振點附近，最大值對應頻率位于反諧振點附近。

2.3 定子諧振振幅計算

由輸入阻抗計算結果可知，諧振頻率非常接近28 200 Hz，因此振幅計算頻率范圍為28 000～28 400 Hz，隔20 Hz計算一次。A、B組壓電陶瓷片正交對稱，只需計算A組壓電陶瓷片激勵振幅。在A組壓電陶瓷上施加幅值為100 V的交變電壓作為激勵。計算得到的定子振幅在頻率28 140 Hz達到最大，這一頻率是所計算的頻率值中最接近諧振點的，并與計算得到的阻抗最小值對應頻率非常接近。當激勵頻率為28 140 Hz時，計算A組壓電陶瓷施加激勵電壓時電機定子的振幅值。以驅動足A與A組壓電陶瓷所夾方塊的共有面的中心點為坐標系XYZ原點，驅動足A與動子相切線的兩端點a1（0，－6e－3，0）、a2（0，－6e－3，2e－3）X方向振幅分別為25．6455μm及18．0013μm，Z方向振幅為19．1181μm及19．3633μm；驅動足B與動子相切線的兩端點b1（0，－6e－3，7e－3）、b2（0，－6e－3，9e－3）X方向振幅分別為24．716 5μm及21．7μm，Z方向振幅為6．622 04μm及6．854 35μm。

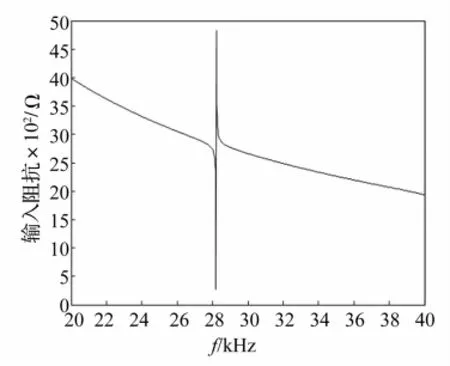
圖5 定子阻抗－頻率特性曲線Fig．5 Impedance-frequence characteristic curve of stator

3 驅動足運行軌跡

對直線超聲波電機關鍵在于如何激勵壓電陶瓷，使定子驅動足與動子接觸點生成橢圓運動，須對定子運動進行分析。為研究接觸點運動軌跡，用幾何學原理據已建有限元模型計算結果分析定子運動機理，推導兩相激勵同時作用的定子驅動足與動子接觸點運動軌跡，并證明接觸點橢圓運動軌跡的存在，為優化電機接觸、設計及驅動控制奠定理論基礎。

定、動子通過彈簧壓在一起，接觸面X方向寬度較小，分析時可認為Z方向值相同接觸點振幅相同。當對A組壓電陶瓷施加激勵電壓時，驅動足接觸點X、Z方向的位移分別為

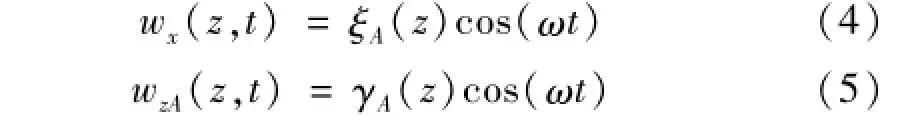
對B組壓電陶瓷施加激勵電壓時驅動足接觸點Y、Z方向位移分別為

對A、B兩組壓電陶瓷施加激勵電壓時Z方向位移為

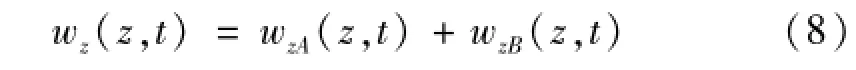
式中：ξA為A組壓電陶瓷施加激勵電壓時驅動足接觸點X方向振幅；γA為A組壓電陶瓷施加激勵電壓時驅動足接觸點Z方向振幅；ξB為B組壓電陶瓷施加激勵電壓時驅動足接觸點Y方向振幅；γB為B組壓電陶瓷施加激勵電壓時驅動足接觸點Z方向振幅；f＝ω／（2π）為振動頻率；φ為相位差。

由于電機定子正交對稱，B組壓電陶瓷施加激勵電壓時振幅值為ξB（z）＝ξA（2t＋h－z），γB（z）＝γA（2t＋h－z）。壓電陶瓷元件激勵使定子產生的振動為微小振動，滿足線性疊加原理。利用有限元分析結果，結合式（4）～式（8），激勵頻率為28 140 Hz得φ＝π／6、π／3、π／2時驅動足接觸點a1、a2、b1、b2點運動軌跡曲線，見圖6～圖8［16］。

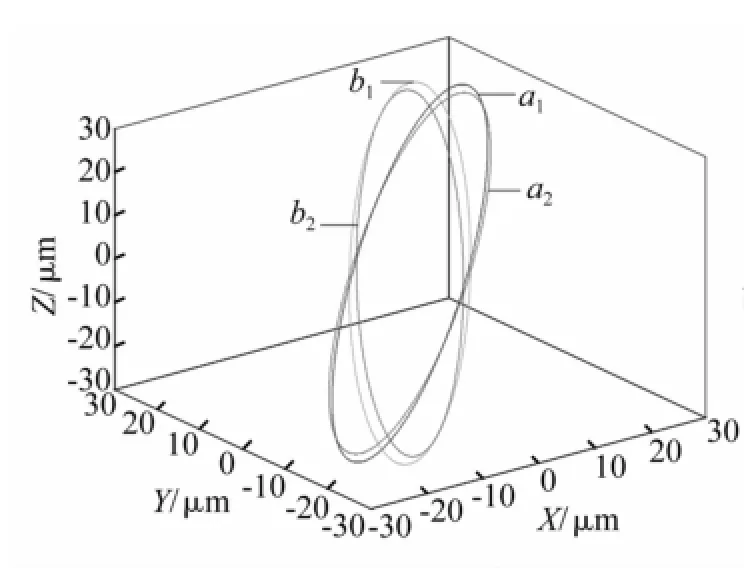
圖6 φ＝π／6時驅動足軌跡示意圖Fig．6 Schematic diagram of the locus of driving feet，whenφ＝π／6

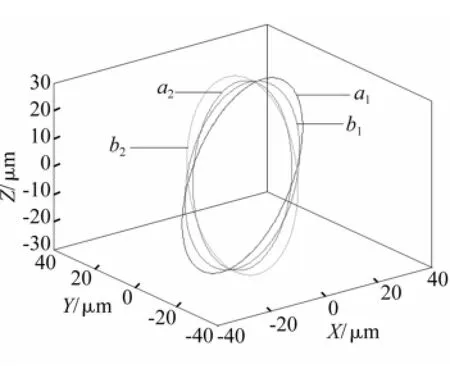
圖7 φ＝π／3時驅動足軌跡示意圖Fig．7 Schematic diagram of the locus of driving feet，whenφ＝π／3

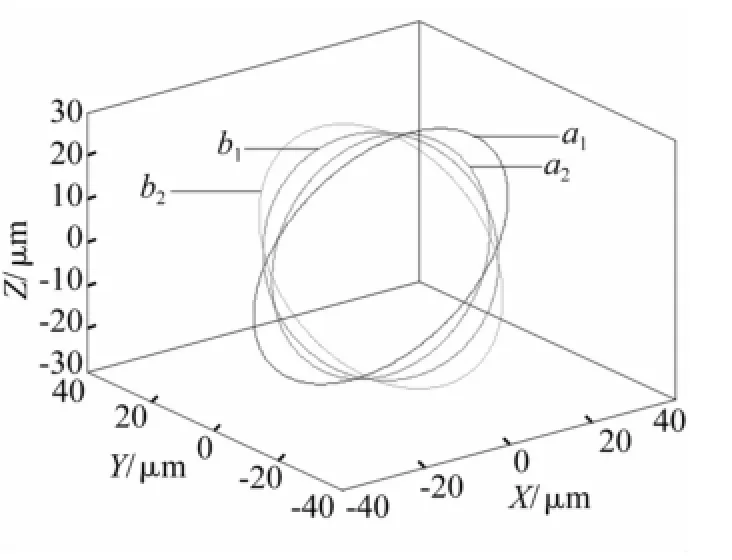
圖8 φ＝π／2時驅動足軌跡示意圖Fig．8 Schematic diagram of the locus of driving feet，whenφ＝π／2

由三圖看出，電機φ＝π／2時運行效率最高，φ此時驅動足接觸點a1、a2、b1、b2點運動軌跡曲線在X－Y平面投影見圖9。

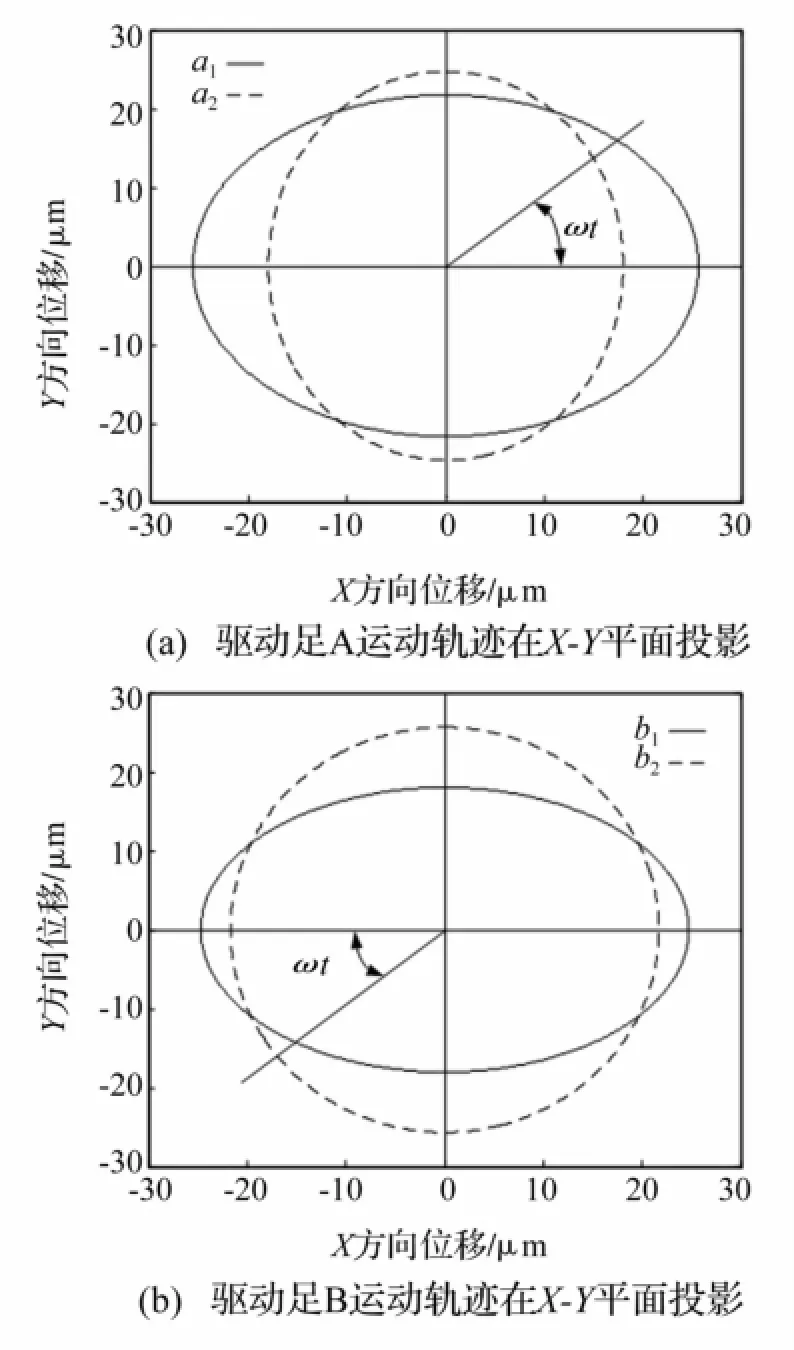
圖9 φ＝π／2時驅動足軌跡示意圖Fig．9 Schematic diagram of the locus of driving feet，whenφ＝π／2

驅動足與動子接觸，由式（6）、（8）可得與動子作用的接觸點在Y－Z平面傾角為

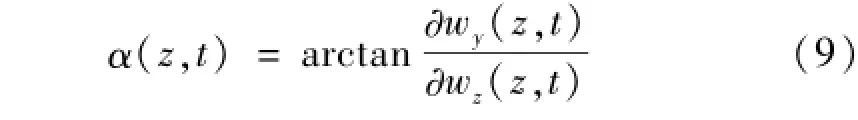
以上分析可證明驅動足接觸點橢圓運動軌跡，并能指導電機驅動足設計、優化定子與動子接觸、提高電機性能。運動軌跡研究亦能為電機驅動控制提供理論基礎。

4 實驗研究

據分析制作實驗用電機，雙足雙壓電晶片直線超聲波電機定子照片見圖10。定子在諧振狀態下阻抗最小，為使定子驅動足能獲得盡量大振幅以提高電機工作效率，電源工作頻率應接近諧振頻率。本文采用NI公司LabVIEW作為虛擬儀器開發平臺，阻抗測試采用LRC測量儀HIOKI3522，PC機與LRC測量儀間通信采用GPIB卡，測量時激勵為恒壓5 V。測量范圍20～40 kHz。所測阻抗－頻率特性曲線見圖11，諧振頻率27．1 kHz。實驗結果與諧響應分析結果對比見表1。

圖10 雙足驅動雙壓電晶片直線超聲波電機定子照片Fig．10 Photo of double-driving feet linear ultrasonic motor stator using bimorphs

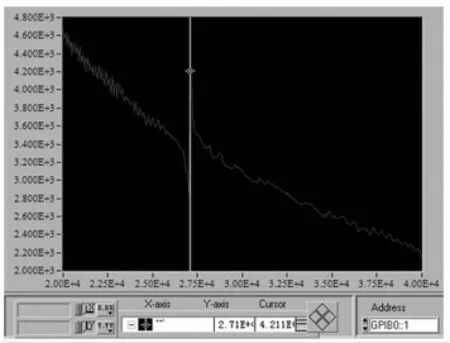
圖11 定子阻抗－頻率特性曲線Fig．11 Impedance-frequence curve of stator

表2 實驗結果與諧響應分析結果對比Tab.2 Contrast between experimen tal results and harmonic response analysis results

由表1看出，理論計算與實驗結果誤差較小。產生誤差的主要原因為：①定子加工存在誤差；②高電壓激勵信號下電機的共振模態與低壓激勵時不同。

5 結 論

（1）本文對用兩組正交雙壓電晶片激勵振動雙足型直線超聲波電機運行機理研究分析，用ANSYS計算獲得定子振動模態。

（2）建立電機定子的振動響應有限元模型，分析定子機電特性，利用ANSYS計算定子輸入阻抗及諧振點定子驅動足接觸點振幅。用幾何學原理計算獲得接觸點振幅，推導不同相位差激勵下定子驅動足與動子接觸點運動軌跡，為優化電機接觸、設計電機驅動控制奠定理論基礎。

（3）用基于LabView的阻抗測量方法測量電機定子的輸入阻抗，并實驗論證理論結果。

［1］Kenjyo T，Sashida T．An introduction of ultrasonic motor［M］．Oxford Science Publications，1993．

［2］Oohira F，Iwase M，Matusi T，et al．Self-hold and precisely controllable optical cross-connect switches using ultrasonic micro motors［J］．IEEE Journal of Selected Topics in Quantum Electronics，2004，10（3）：551－557．

［3］Kawano H，Ando H，Hirahara T，et al．Application of a multi-dof ultrasonic servomotor in an auditory tele-existence robot［J］．IEEE Transactions on Robotics，2005，21（5）：790－800．

［4］Wai R J，Su K B．Supervisory control for linear piezoelectric ceramic motor drive using genetic algorithm［J］．IEEE Transactions on Industrial Electronics，2006，53（2）：657－673．

［5］Tominaga M，Kaminaga R，Friend JR，et al．An ultrasonic linearmotor using ridge-mode traveling waves［J］．IEEE Transactions on UFFC，2005，52（10）：1735－1742．

［6］Sadriyeh SMR，Zolghadri MR，Mahdavi J，et al．Design and simulation of linear piezoelectric stepper motor drive using resonant converter［C］．38th IAS Annual Meeting，2003：1711－1717．

［7］Friend J，Umeshima A，Ishii T，et al．A piezoelectric linear actuator formed from a multitude of bimorphs［J］．Sensors and Actuators A，2004，109（3）：242－251．

［8］曲建俊，齊毓霖，張志謙，等．超聲馬達摩擦學及其摩擦材料研究進展［J］．摩擦學學報，1998，18（1）：80－87．

QU Jian-jun，QIYu-lin，ZHANG Zhi-qian，et al．Advances on tribology of ultrasonic motor and its friction materials［J］．Tribology，1998，18（1）：80－87．

［9］李存岑，楊明，李世陽．超聲電機振子振型激勵技術研究進展［J］．振動與沖擊，2009，28（9）：175－179．

LICun-cen，YANG Ming，LI Shi-yang．Exciting technique for vibrating shape of ultrasonic motor vibrators［J］．Journal of Vibration and Shock，2009，28（9）：175－179．

［10］莫岳平，胡敏強，金龍，等．振動模態與超聲波電機性能關系的研究［J］．電工技術學報，2002，17（3）：7－11．

MO Yue-ping，HU Min-qiang，JIN Long，et al．Research on the relation between vibration mode and ultrasonic motor＇s performance［J］．Transactions of China Electrotechnical Society，2002，17（3）：7－11．

［11］夏長亮，鄭堯，史婷娜，等．行波接觸型超聲波電機定子振動有限元分析［J］．中國電機工程學報，2001，21（2）：25－32．

XIA Chang-liang，ZHENG Yao，SHI Ting-na，et al．Fem analysis on stator vibration of traveling wave type contact ultrasonic motor［J］．Proceedings of the Csee，2001，21（2）：25－32．

［12］張健滔，朱華，趙淳生．行波型桿式超聲電機定子的參數化有限元法優化設計［J］．振動與沖擊，2009，28（7）：122－125．

ZHANG Jian-tao，ZHU Hua，ZHAO Chun-sheng．FEM-based parametric optimum design of a traveling-wave type barlike ultrasonic motor stator［J］．Journal of Vibration and Shock，2009，28（7）：122－125．

［13］Ueha S，Tomikawa Y．Ultrasonic motors-theory and application［M］．Oxford Science Publications，1993．

［14］陳永校，郭吉豐．超聲波電動機［M］．杭州：浙江大學出版社，1994．

［15］徐志科，胡敏強，金龍，等．基于FEA的行波型超聲波電機阻抗特性分析［J］．中國電機工程學報，2005，25（18）：131－134．

XU Zhi-ke，HU Min-qiang，JIN Long，et al．Analysis of traveling wave type ultrasonic motor input impedance characteristic using FEA method［J］．Proceedings of the CSEE，2005，25（18）：131－134．

［16］陳維山，郝銘，趙學濤，等．縱彎復合多自由度球形超聲電機的研究［J］．振動與沖擊，2009，28（7）：105－110．

CHEN Wei-shan，HAO Ming，ZHAO Xue-tao，et al．A muti-dof spherical ultrasonic motor with longitudinal-benging hybrid vibration modal analysis［J］．Journal of Vibration and Shock，2009，28（7）：105－110．

Operation mechanism of linear ultrasonic motor installed with bimorphs and double-driving feet

CHEN Qiang1，XU Zhi-ke2，JIANG Chun-rong1，LU Dan-hong1
（1．School of Electric Power Engineering，Nanjing Institute of Technology，Nanjing 211167，China；2．School of Electrical Engineering，Southeast University，Nanjing 210096，China）

The operationmechanism of a new type linear ultrasonicmotorwas analyzed．Themotor，installed with bimorphs and double-driving feet，has the attribute of simple structure，no frequency degeneration and easiness to be miniaturized．The construction，vibration mode and operation principle were described．A finite elementmodel of the stator was established to investigate its vibration responses．The computation method of input impedance of the stator togetherwith the computation resultswas presented．The vibration amplitudes at the driving-feet's contact points close to the harmonic frequency were computed．The movement loci of the driving-feet's contact points were derived．The impedance characteristic of stator was surveyed by using impedance characteristic analysis instrument，and the experimental resultswere compared with the theoretical ones．

linear ultrasonic motor；bimorphs；double-driving feet；finite element model；movement locus；impedance characteristic

TM383

：A

10．13465／j．cnki．jvs．2014．22．004

國家自然科學基金資助項目（51207021）；江蘇省自然科學基金項目（BK20140766）；南京工程學院校級科研基金資助項目（YKJ201315，YKJ201317）

2013－03－25 修改稿收到日期：2013－12－29

陳強男，博士，1981年10月生