多激勵識別的自適應延遲逆系統方法

周 盼，李玩幽，率志君

（哈爾濱工程大學動力與能源工程學院，哈爾濱 150001）

多激勵識別的自適應延遲逆系統方法

周 盼，李玩幽，率志君

（哈爾濱工程大學動力與能源工程學院，哈爾濱 150001）

針對現有逆系統方法依賴狀態空間模型的缺點提出采用系統自適應延遲逆模型識別多激勵時間歷程。采用自適應算法對系統進行延遲逆模型辨識，結合逆模型利用工作狀態響應數據識別時域載荷。以簡支梁為研究對象用無噪聲干擾、有噪聲干擾加速度響應識別多點穩態激勵及多點非穩態激勵。仿真結果表明，噪聲干擾時識別精度有所降低，但較滿意，驗證該方法對多激勵源識別的可行性。

振動；時域載荷識別；自適應延遲逆模型；時間延遲

動態載荷不僅為機械設計的原始依據亦為結構動力修改與優化依據，其識別問題廣受關注［1］。載荷識別主要有頻域、時域方法。頻域法只需對系統特性矩陣作逆運算即可，較易實現，但只能識別線性系統的穩態激勵；而時域法不僅適用于線性系統，亦適用于非線性系統，且能有效處理瞬態沖擊激勵的識別問題，其研究不斷深入。

逆系統法為由魏星原等［2］提出的時域識別方法。利用系統輸入輸出信息建立自回歸滑動平均（ARMA）逆模型求解輸入激勵，將載荷識別逆問題轉化為正問題處理；但線性系統只在可逆、穩定、能控、能觀條件下存在逆系統，因而該方法應用受到限制。鑒于逆系統存在條件苛刻缺點，Steltzner等［3］采用截斷奇異值分解法（TSVD）計算由Markov參數構成的系統特性矩陣的偽逆建立的非因果逆向濾波器（Inverse Structural Filter，ISF），進而識別結構所受載荷時間歷程；但ISF可能不穩定，對此Allen等［4］以系統狀態空間模型為基礎，提出改進算法－延遲多步逆向濾波器（Delayed，Multistep ISF，DMISF）識別時域載荷。Nordstr?m等［5］基于系統離散狀態空間模型，研究對位系統（collocated system）、非對位系統（non-collocated system）載荷識別問題，并用時間延遲方法將非對位系統載荷識別病態問題轉化為良態問題。因逆系統方法發展過程中基本未脫離系統狀態空間模型，需先了解系統先驗知識，故限制逆系統方法的應用。

基于此，本文提出基于自適應延遲逆模型的時域識別方法。采用自適應橫向濾波器模擬逆模型，不依賴狀態空間模型，無需掌握系統數學模型；在逆向建模過程中無需對特性矩陣逆運算，可避免求逆過程中的病態問題。

1 載荷識別原理

基于延遲逆模型的載荷識別方法以某準則（如均方誤差最小或加權誤差平方和最小）為依據建立系統的延遲逆模型，以實際激勵的系統響應信號為逆模型輸入，逆模型輸出即為實際激勵的延遲估計值。

1.1 延遲逆模型辨識原理

建立準確系統逆模型、使其能真實反映系統的逆特性為時域載荷識別的前提條件。本文采用有限脈沖響應（finite impulse response）自適應橫向濾波器模擬系統逆模型。自適應濾波器由自適應線性組合器與單位延遲單元組成，見圖1。

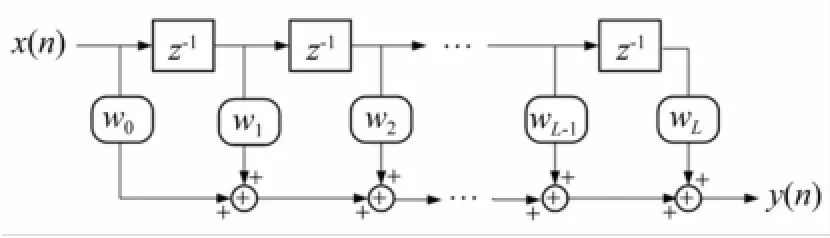
圖1 有限脈沖響應濾波器Fig．1 Finite impulse response filter（FIR filter）

采樣時刻n的輸出信號y（n）與輸入信號關系為

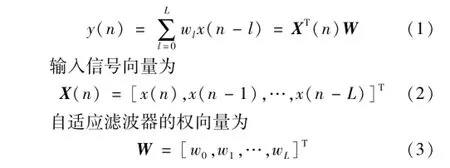
式中：L＋1為自適應濾波器長度。

用自適應濾波器模擬逆模型，SISO系統延遲逆模型辨識原理圖見圖2。將機械系統在白噪聲激勵fw（n）下響應信號xw（n）作為逆模型輸入信號，逆模型輸出信號f0（n）與延遲激勵fd（n）之差定義為誤差信號e（n），調整自適應濾波器權向量，實現滿足某準則的最優濾波。

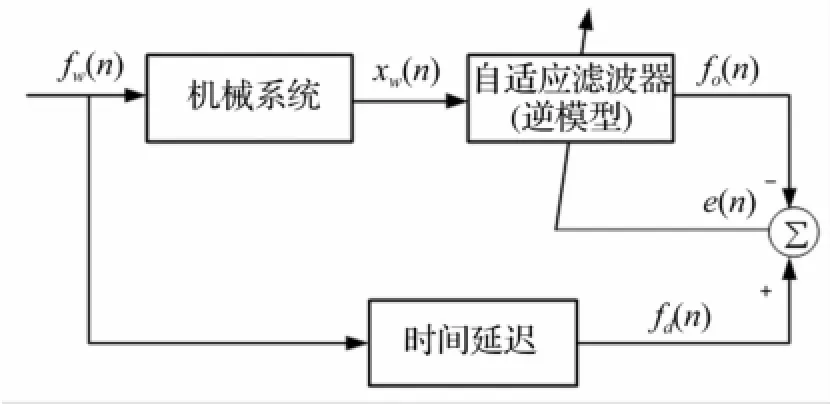
圖2 SISO系統延遲逆模型辨識原理圖Fig．2 Schematic diagram of delayed inversemodel identification for SISO system

由圖2，n時刻逆模型輸出信號f0（n）為

由式（8）看出，均方誤差性能函數是權向量的二次型函數，具有“碗狀形”曲面，自適應過程即為連續不斷調節權向量尋求碗底部。本文采用歸一化LMS（Normalized Least Mean Square，NLMS）算法［6］調整自適應濾波器權向量，n＋1時刻權向量W（n＋1）由n時刻權向量W（n）更新獲得，即

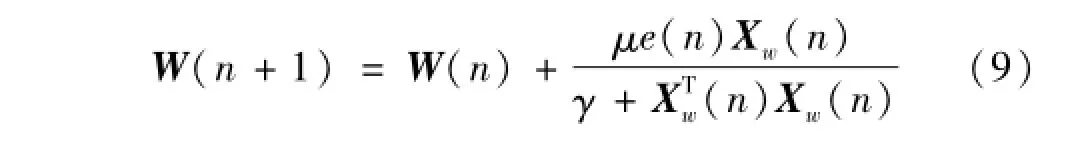
式中：μ為收斂因子；γ∈［0，1］為泄露因子。

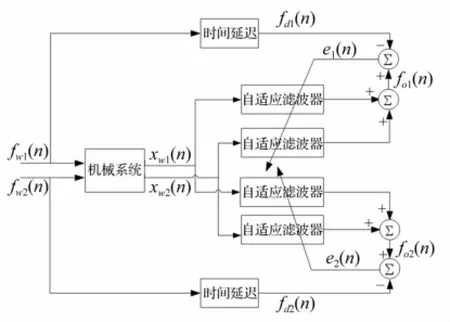
圖3 雙輸入雙輸出系統延遲逆模型辨識Fig．3 Delayed inversemodel identification for double-input-double-output system

對多輸入多輸出（MIMO）系統，其延遲逆模型建模方法與SISO系統類似。對單輸入激勵單輸出響應的SISO系統，單個自適應濾波器即能描述逆模型振動特性；但對MIMO系統則需建立每個輸入、輸出間關系才能完整描述逆系統振動特性。以雙輸入雙輸出系統為例，其延遲逆模型建模原理見圖3，采用4個自適應濾波器模擬該雙輸入雙輸出系統延遲逆模型。該延遲逆模型兩輸出信號fo1（n），fo2（n）與輸入信號xw1（n），xw2（n）（機械系統輸出響應）間關系可表述為

自適應過程收斂時延遲逆模型辨識過程完成。在逆模型辨識過程中加入延遲環節，可得系統延遲逆模型。對圖2、圖3中時間延遲進行說明。若無時間延遲環節，對最小相位系統（系統零極點均位于Z平面單位圓內）其逆是穩定的、因果的；然而對非最小相位系統（系統零點有的位于Z平面單位圓外）因不穩定零點存在，逆模型不穩定。因此需引入合適的時間延遲以獲得穩定的延遲逆模型［7－8］，亦可獲得更小均方誤差。

圖4 有噪聲干擾的SISO系統延遲逆模型辨識Fig．4 Delayed inversemodel identification for SISO system under noise disturbance condition

理論研究表明，無噪聲干擾時圖2中最小均方誤差為零，此時自適應濾波器權向量能準確反映系統的時域逆特性［9］；但當系統響應中存在噪聲干擾時，用圖2辨識SISO系統的延遲逆模型會導致較大誤差，應按圖4對延遲逆模型進行辨識［10］。先進行系統辨識，再由系統正模型對延遲逆模型進行自適應建模。所得正模型基本與機械系統動態響應相同，但不受噪聲干擾，故可求得不受噪聲干擾的延遲逆模型。對MIMO系統而言，有噪聲干擾時其延遲逆模型辨識過程與SISO系統類似。

1.2 基于延遲逆模型的載荷識別

系統延遲逆模型建模完成后即可進行載荷識別。將系統在實際激勵狀態下響應信號xm（n）作為延遲逆模型輸入，則逆模型輸出fe（n）即為實際激勵延遲估計。SISO系統時域載荷識別原理見圖5。

圖5 SISO系統時域載荷識別Fig．5 Real time load estimation for SISO system

逆模型輸出信號fe（n）可表示為響應信號與延遲逆模型權值的乘積之和，即

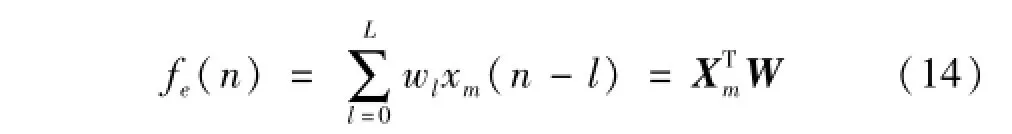
式中：W為延遲逆模型辨識過程中由式（9）所得權向量。

由于延遲逆模型實際為系統非因果逆模型，因此采用過去、未來時刻響應識別當前時刻激勵。

2 載荷識別仿真研究

以兩端簡支梁為研究對象進行多激勵源識別仿真研究。簡支梁幾何參數及材料屬性見表1。

表1 簡支梁幾何參數及材料參數Tab.1 Geometric and material param eters of sim p ly supported beam

激勵力F1作用于簡支梁0．5 m處，F2作用于0．2 m處。用0．3 m、0．1 m位置處加速度響應識別兩激勵力，見圖6。加速度測點位置與激勵位置不同，為典型非對位系統，屬非最小相位系統。因此，時間延遲環節不能省略，對逆模型穩定性及準確性至關重要。

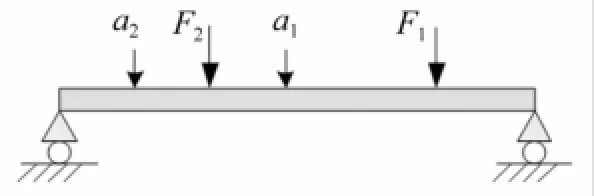
圖6 激勵力及響應測點位置Fig．6 Locations of excitation and response points

2.1 無噪聲干擾識別結果

由圖3的辨識無噪聲干擾時雙輸入雙輸出系統延遲逆模型。為盡可能準確模擬寬頻范圍內系統逆特性，選白噪聲信號作為激勵形式，用Matlab軟件中randn實現。采用lsim命令求解該系統在兩白噪聲激勵下響應測點位置加速度（圖6）。仿真中設定時間分辨率1E－5 s，自適應濾波器長度600，時間延遲320，收斂因子0．2，泄露因子1。待識別單頻激勵、沖擊激勵（半正弦激勵）表達式為

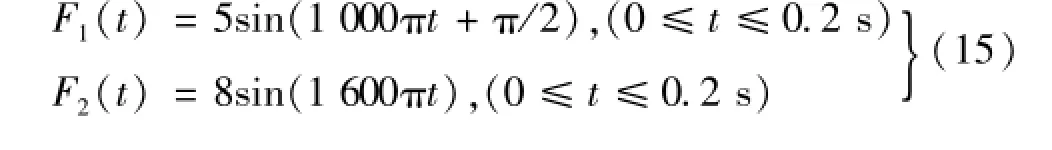
用加速度響應識別單頻激勵、沖擊激勵及白噪聲激勵，結果見圖7。分析圖7知，無噪聲干擾時該方法能準確識別單頻、白噪聲激勵。沖擊激勵識別結果與真實結果基本吻合，但在主峰兩側存在小旁瓣，說明延遲逆模型不完善。可通過增加自適應濾波器長度進行改善。

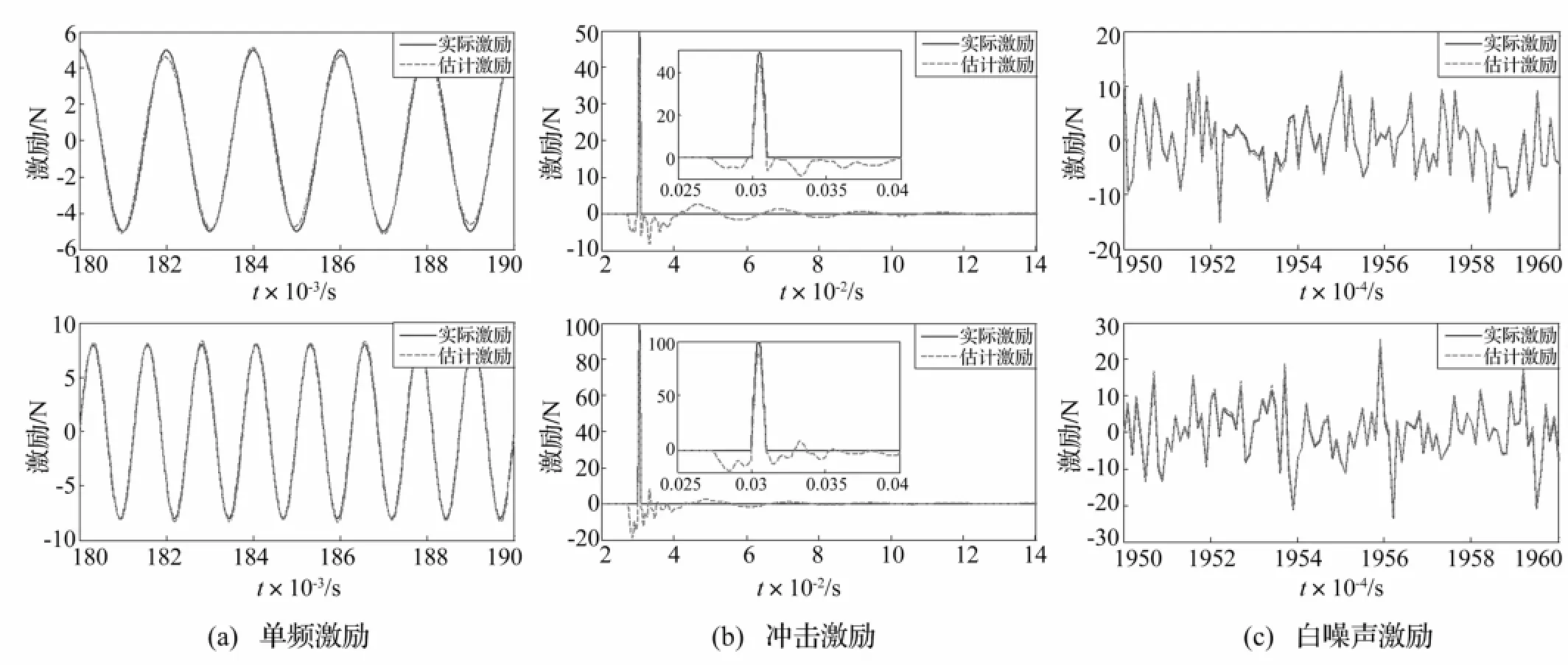
圖7 兩點激勵識別結果Fig．7 Reconstruction result of two input forces

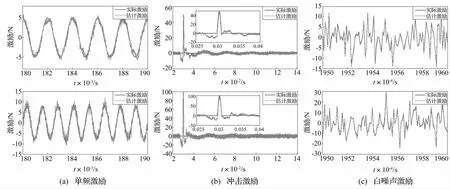
圖8 兩點激勵識別結果Fig．8 Reconstruction result of two input forces

無噪聲干擾激勵識別結果說明，基于延遲逆模型的載荷識別方法能識別穩態激勵及非穩態激勵，從而可驗證該方法的可行性。

2.2 有噪聲干擾識別結果

對實際工程環境，測試響應中會存在噪聲干擾，需研究噪聲干擾對時域方法識別精度影響。本文所用噪聲模型［11－12］噪聲幅值為響應均方根值的10%，含噪聲干擾的響應可表示為

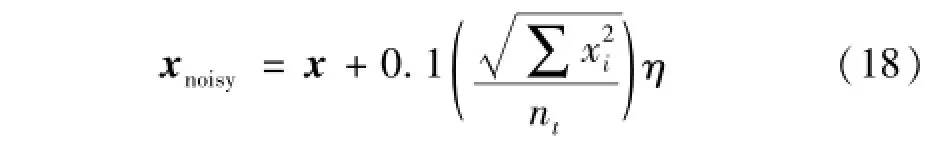
式中：nt為數據點數目；x為真實響應向量；η為由均值0方差1的正態分布隨機數組成長度nt的向量。

用噪聲干擾模型對加速度響應添加噪聲，按圖4進行延遲逆模型辨識并識別時域激勵。仿真時間分辨率1E－5 s，正模型長度1 500，逆模型長度600，延遲320。不同形式激勵識別結果見圖8。由圖8看出，噪聲干擾較大時，激勵識別精度較無噪聲降低，但能滿足工程需要。對正弦激勵，識別的幅值、相位與真實激勵基本一致，但存在較多毛刺，由響應中噪聲所致。白噪聲激勵識別結果與真實激勵吻合較好，此因其與用于系統逆模型辨識激勵形式一致。沖擊激勵幅值結果較準確，但主峰兩側存在小旁瓣。

3 載荷識別試驗研究

對雙層隔振系統進行載荷識別試驗研究，驗證本文所提時域識別方法的有效性、可行性。雙層隔振系統試驗臺架見圖9。用彈簧吊裝激振器，信號發生器產生激勵信號，通過功率放大器輸給激振器，再通過激振桿將激振力傳遞給雙層隔振系統作用于上層質量結構。通過力傳感器、加速度傳感器采集激振力信號及結構加速度響應。

圖9 雙層隔振系統試驗臺架Fig．9 Two－stage vibration isolation system test bench

逆模型權向量長度300，時間延遲160。單頻激勵、偽隨機激勵識別結果見圖10。分析圖10知，該方法能較準確識別正弦激勵及偽隨機激勵。

4 結 論

（1）采用自適應延遲逆模型識別作用于簡支梁的多點激勵，通過研究響應中干擾噪聲對識別精度影響，驗證本文識別方法的有效性。

（2）該識別方法不僅適用于穩態、瞬態激勵，且在有噪聲干擾時亦能獲得較準確的激勵識別結果。

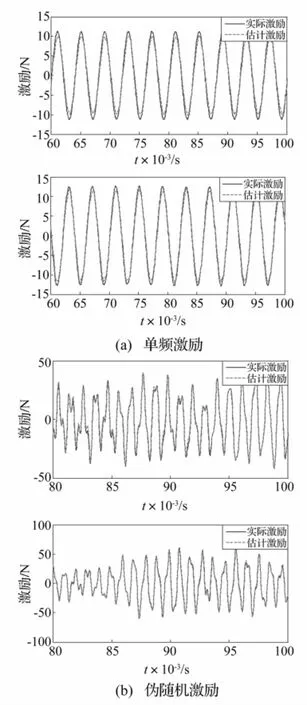
圖10 不同激勵形式下激勵識別結果Fig．10 Estimated results of operational forceswith different excitation types

（3）該識別方法原理簡單，無需對系統特性矩陣求逆運算，可避免病態問題；對缺少先驗知識系統辨識時更具優勢。

［1］吳淼，黃民．機械系統的載荷識別方法與應用［M］．北京：中國礦業大學出版社，1995．

［2］魏星原，宋斌，鄭效忠．載荷識別的逆系統方法［J］．振動、測試與診斷，1995，15（3）：37－43．

WEIXing-yuan，SONG Bin，ZHENG Xiao-zhong．A method of inverse system to identify force［J］．Journal of Vibration，Measurement＆Diagnosis，1995，15（3）：37－43．

［3］Steltzner A D．Input force estimation，inverse structural system and the inverse structural filter［D］．The University of W isconsin-Madison，Ph．D thesis，1999．

［4］Allen MS，Carne T G．Delayed，multi－step inverse structural filter for robust force identification［J］．Mechanical Systems and Signal Processing，2008，22（5）：1036－1054．［5］Nordstrm L JL，Nordberg TP．A time delaymethod to solve non-collocated input estimation problems［J］．Mechanical Systems and Signal Processing，2004，18：1469－1483．

［6］Haykin S．Adaptive filter theory（third edition）［M］．Prentice Hall，1996．

［7］Widrow B．Adaptive inverse control［C］．／／IFAC Adaptive Systems in Control and Signal Processing，Lund，Sweden，1986．

［8］Widrow B，Plett G L．Adaptive inverse control based on linear and nonlinear adaptive filtering［C］．／／Proceedings of InternationalWorkshop on Neural Networks for Identification，Control，Robotics and Signal／Image Processing，1996：30－38．

［9］Widrow B，Stearns S D．Adaptive signal processing［M］．Prentice Hall，1985．

［10］Widrow B，Walach E．Adaptive inverse control，reissue edition：a signal processing approach［M］．Wiley-IEEE Press，2007．

［11］Steltzner A D，Kammer D C．Input force estimation using an inverse structural filter［J］．17th International Modal Analysis Conference（IMAC XXVII），Kissimmee，1999，3727（2）：954－960．

［12］Steltzner A D，Kammer D C，Milenkovic P．A time domain method for estimating forces applied to an unrestrained structure［J］．Journal of Vibration and Acoustics，2001，123：524－532．

Adaptive delayed inverse system method for reconstruction ofmultiple input excitations

ZHOU Pan，LIWan-you，SHUAIZhi-jun
（Harbin Engineering University，College of Power and Energy Engineering，Harbin 150001，China）

An adaptive delayed inverse model of mechanical system was adopted to determine time histories of multiple input forces aiming at improving the shortcoming that the existing inverse system method relies on the state-space model．An adaptive algorithm was applied to identify the delayed inversemodel，followed by time domain force estimation using operational response data combined with the inversemodel ofmechanical system．Themulti-input forces of a simply supported beam were reconstructed by using accelerations without and with noise disturbances．The simulation results illustrate that the reconstruction accuracy decreases under noise condition，yet isstill relatively satisfied and themethod for multi-input identification is feasible．Furthermore，the method was validated experimentally．

vibration；time domain force estimation；adaptive delayed inversemodel；time delay

TU312；O327

：A

10．13465／j．cnki．jvs．2014．22．008

國家自然科學基金（50979016）；中央高校基本科研業務費專項資金項目（HEUCFZ1115）

2013－07－24 修改稿收到日期：2013－11－15

周盼女，博士生，1986年11月生

李玩幽男，博士，教授，博士生導師，1972年10月生郵箱：hrbeu＿ripet＿lwy＠163．com