P-M與TV模型在加性高斯白噪聲去噪中的比較研究

楊 巧,李五強,韓國棟

(陜西師范大學數學與信息科學學院,西安 710062)

【數學與應用數學研究】

P-M與TV模型在加性高斯白噪聲去噪中的比較研究

楊 巧,李五強,韓國棟

(陜西師范大學數學與信息科學學院,西安 710062)

噪聲是圖像獲取、傳輸和儲存過程中不可避免的現象.去噪作為圖像處理的首要步驟與基本問題是后續的高層次圖像處理的基礎.以加性高斯白噪聲為例,綜述了P-M擴散方程及TV模型的原理,并從視覺與定量指標兩個方面比較了去噪效果.最后,在熱擴散方程模型預處理條件下比較了兩種模型的去噪效果.

圖像去噪;P-M擴散方程;TV模型;熱擴散方程

圖像在采集、傳輸與存儲過程中,由于受到各種噪聲的干擾,常出現失真現象.圖像去噪作為圖像預處理的基礎,直接影響著后續高層次的處理效果[1].根據噪聲特點不同,已給出多種去噪算法.去噪算法主要分為空域去噪算法和頻域去噪算法[2],本文不討論頻域算法.傳統的空域去噪方法有：均值濾波器、中值濾波器等[1-3].均值濾波器在一定程度上對高斯噪聲能加以抑制,但不能很好地保護細節數據,使得圖像出現模糊現象;中值濾波器對椒鹽噪聲的抑制效果較好,而對于高斯噪聲的抑制效果并不理想,同樣會出現模糊現象.這些傳統的去噪算法去噪的同時不能保持圖像的邊緣特征,從20世紀80年代以來,偏微分方程與變分方法的圖像去噪方法得到不斷發展[4].1990年,Perona與Malik證明了傳統的圖像去噪模型是各向同性的,在去噪的同時會使圖像邊界模糊[5].而偏微分方程可以實現各向異性擴散,在去噪的同時可以保持邊緣特征.1992年,Rudin等人提出了TV模型,將Tikhonov正則化中的范數改為L1范數,即偏微分方程實現各向異性擴散,因此,TV模型去噪的同時可以保持邊緣特征[6].

本文將以加性高斯白噪聲為例,比較P-M擴散方程與TV模型的去噪與邊緣保持效果,并且在熱擴散方程模型預處理的條件下,再次比較兩種模型的去噪效果.

1 預備知識

1.1 加性噪聲模型

設Ω是實平面R2上圖像的支撐集,f是失真或退化圖像,含有加性噪聲數字圖像模型可描述如下：

其中：u表示理想圖像,n表示噪聲.本文將探討均值為0,方差為σ2的加性高斯白噪聲的去噪問題.

1.2 熱擴散方程模型

熱擴散方程作為最典型的被用于加性噪聲去除的偏微分方程[7],它的形式為

當它被用于圖像去噪時,u的初始值f就是含有噪聲的圖像,熱擴散過程就是去噪過程.

熱擴散方程的初值問題可以使用有限差分法進行求解,其離散格式為：

1.3 P-M擴散模型

因熱擴散方程模型在去噪同時不能保持圖像的原有邊緣,其實用性受到較大的限制.1990年,Perona 與Malik提出了著名的P-M圖像去噪模型[5],這一模型的提出開辟了偏微分方程在圖像領域中的新應用.Perona與Malik證明了傳統的圖像去噪模型是各向同性的,在去噪的同時會使圖像邊緣模糊.因此,可以利用恰當的偏微分方程實現各向異性擴散,從而在去噪的同時保持圖像的邊緣特征.P-M各向異性擴散方程是：

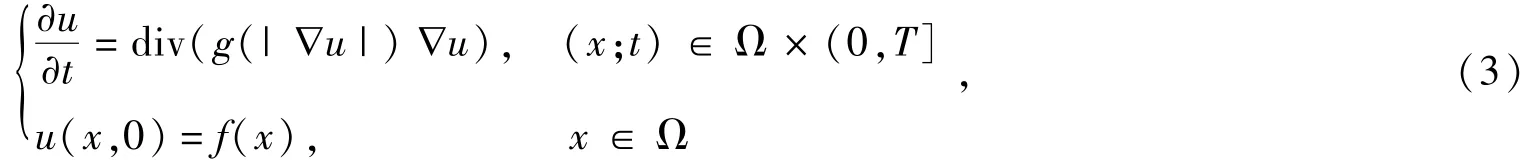
Perona與Malik建議系數函數g取如下兩種：

這時所得的結果最為理想.由于式(4)(5)的本質相同,經試驗在相同條件下去噪效果基本相同.因此,在下面數值實驗中我們選取的系數函數為式(5).

P-M模型的離散格式為：

其中各方向的差分梯度為：

1.4 Total Variation模型

前述兩種去噪方法以某類擴散方程為工具,噪聲圖像被視為方程的初值,經方程的演化得到理想圖像.處理加性噪聲模型(1)的另一個思路是,在某個恰當的函數空間內尋找u,使得噪聲

盡可能地小.最小二乘法是函數逼近最常用的方法,可表示為：

其中等式右邊第一項為保真項,反映真實解與近似解的接近度,其作用是保證圖像恢復前后變化不大;第二項為光滑項,估計圖像能量,保證圖像光滑.參數λ越大,保真項所起的作用就越大,解就越接近初值;λ越小,那么擴散作用就越大,相應的圖像就越光滑.如果λ=0,圖像就過于光滑,圖像邊緣就會出現嚴重的模糊現象;如果λ=∞,圖像會出現劇烈震蕩.這樣就要求λ的取值要適當.式(8)被稱為全變差(Total Varitation)去噪模型,簡稱為TV模型.與Sobolev范數相比,全變差范數對圖像的光滑性要求低[11-12],符合圖像處理問題的實際.

TV降噪模型相應的Euler-Lagrange方程為

對式(9)使用最速下降法,加上?Ω上的Neumann邊界條件和初始值u(x;0),得到反應擴散方程的初邊值問題：

利用有限差分法,初邊值問題式(10)可離散化成

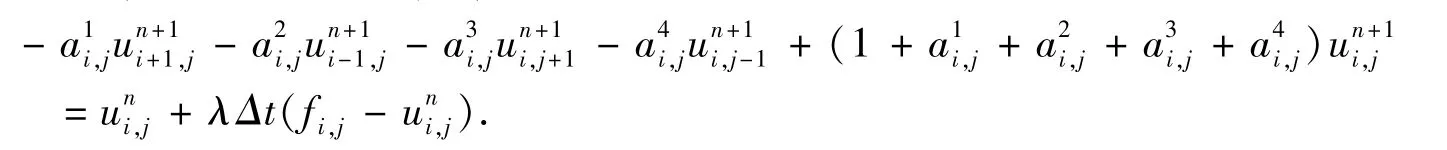
其中：

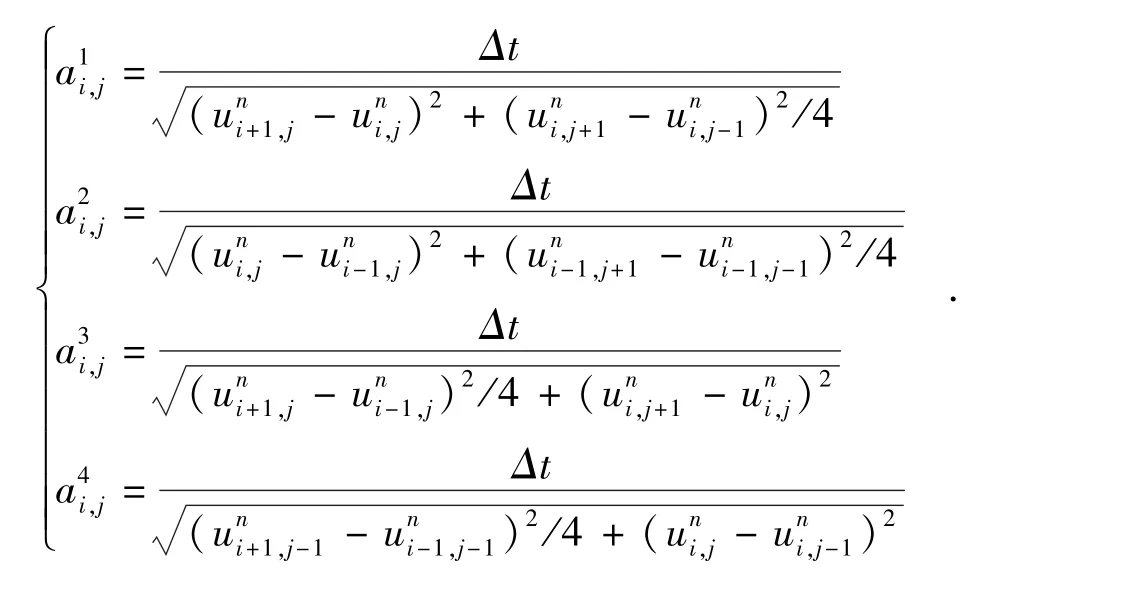
2 數值實驗

2.1 定量指標

我們將通過數值實驗,從視覺和定量指標兩個方面比較熱擴散方程模型、P-M擴散模型以及TV模型對于高斯白噪聲的去噪效果.用到的定量指標如下：

峰值信噪比測度：

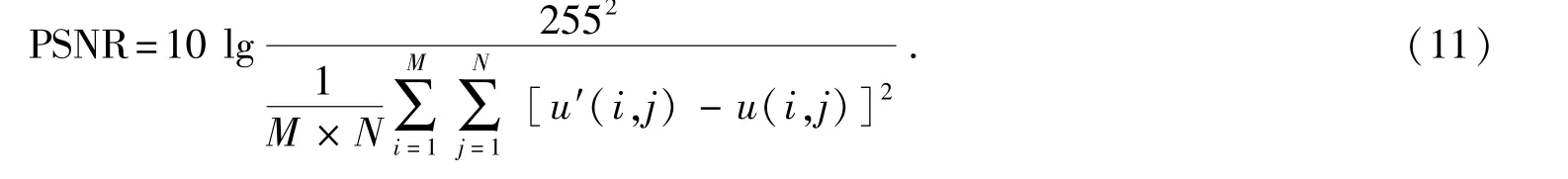
均方差測度：

結構相似性測度：

其中：u是原圖像;u憶是去噪后的圖像;M和N是圖像的尺寸;i,j是圖像在i,j的像素;σu憶與σu是u憶與u的標準差;μu憶與μu是u憶與u的均值;σu憶u是u憶與u的協方差.在以上3個指標中,PSNR越大,表明去噪效果越好,而MSE則相反,SSIM的值越接近于1,表明去噪后的圖像與原圖像越接近.

在以下實驗中,對“Barara”圖像加入均值為0,方差為0.002的高斯白噪聲.我們將以此噪聲圖像為處理對象,比較兩種去噪模型的效果.

2.2 兩種模型的數值分析

P-M方程模型的去噪效果不僅和步長Δt、迭代次數N有關,還和參數K有關.我們首先固定N(N分別取20,40,50,55,60,70,100),再固定K(K分別取10,15,25,30,35,40,45,50),隨著Δt的增加,從中找出同一迭代次數N,在不同K處,P-M模型去噪的最佳步長Δt,比較實驗數值給出相同迭代次數下最佳的K值與步長Δt.經過大量實驗,得到的定量指標數據如表1所示.

表1 P-M模型下不同迭代次數下最優定量指標比較

從表1可以看出,P-M方程模型的去噪效果在N=60,K=30,Δt=0.01附近達到最佳.

TV模型的去噪效果不僅和步長Δt、迭代次數N有關,還和參數λ有關.我們首先固定N(N分別取5, 10,20,40,50,70,100),再固定λ(λ分別取5,6,7,8,9,10),隨著Δt的增加,從中找出相同迭代次數下,在不同λ處,TV模型去噪的最佳步長Δt;接下來比較相同迭代次數下不同λ處的最佳去噪效果,最終找出每個迭代次數下最佳的λ與Δt.經過大量實驗,得到的定量指標數據如表2所示.

表2 TV模型下不同迭代次數下最優定量指標比較

由表2可知,TV方程模型的去噪效果在N=40,λ=7,Δt=0.16附近達到最佳.

通過對上述兩模型的分析,我們把兩個模型處理加性高斯噪聲的相對最佳效果列出,得到表3.

表3 兩種模型最優狀態定量指標比較

在均得出最佳去噪效果的條件下,二者的運行時間差別不大,P-M與TV模型用時分別為：0.597 166 s和0.545 507 s.

以下是兩個模型最佳效果圖的局部擴大圖與邊緣提取圖的展示,其效果如圖1所示.

圖1 Barara圖像實驗結果

由圖1的第一行局部擴大圖可以看出：P-M模型與TV模型的去噪圖效果在視覺上相差不大.但是,從定量指標的分析上可以看出,TV模型相比P-M模型的去噪效果要好.此外,由圖1的第二行邊緣提取圖可以看出：在長方形分割區域內可以看出,TV模型的邊緣保持能力比P-M模型好一些.綜合視覺與定量指標的TV模型對于加性高斯白噪聲的去噪效果優于P-M模型.

3 熱擴散方程處理下兩種模型的數值比較圖像

表4 熱擴散模型下兩種模型最優狀態定量指標比較

眾所周知,P-M模型與TV模型可以在去噪同時保持圖像的邊緣.然而,保持邊緣的能力在某種程度上也影響了它們的去噪效果.一種常用的手段是,在應用P-M模型與TV模型之前進行濾波預處理.顯然,為保證后續處理的效果,應采用迭代次數少、步長小的濾波.我們首先利用熱擴散方程模型(迭代次數N=2,步長Δt=0.005)對噪聲圖像進行去噪處理,接下來再應用表1與表2中P-M模型與TV模型相對的最佳數值進行處理,最后得到的定量指標如表4所示.

顯然,經熱擴散模型預處理后,兩種模型的定量指標分別優于這兩種模型的單獨使用;同時,熱擴散模型預處理后的TV模型效果優于熱擴散模型預處理后的P-M模型.

4 結論

本文比較了傳統的P-M模型與TV模型的降噪效果,得到的結論是：從視覺和定量指標兩個方面來看,TV模型的效果優于P-M模型;并且在P-M模型與TV模型之前使用熱擴散模型預處理,分別優于單獨應用P-M模型與TV模型,而熱擴散模型預處理之后,TV模型仍優于P-M模型.

[1]馮象初,王衛衛.圖像處理的變分和偏微分方程方法[M].北京：科學出版社,2009.

[2]Rafael C Gonzalez,Richard E.Woods.Digital Image Processing[M].Second Edition.Beijing：Publishing House of Electronics Industry,2002.

[3]劉世法,周旭,孫怡寧,等.一種新型均值濾波器及在壓力分布中的應用[J].計算機應用,2009,29(6)：1728-1730.

[4]吳斌,吳亞東,張紅英.基于變分偏微分方程的圖像復原技術[M].北京：北京大學出版社,2008.

[5]Perona P,Malik J.Scale space and edge detection using anisotropic diffusion[J].IEEE Trans.On Pattern Analysis and Machine Intelligence,1990,12(7)：629-639.

[6]Leonid I.Rudin,Stanley Osher,Emad Fatemi.Nonlinear total variation based noise removal algorithms[J].Physica D,1992, 60：259-268.

[7]王大凱,侯榆青,彭進業.圖像處理的偏微分方程方法[M].北京：科學出版社,2008.

[8]Weickert J,Benhamouda B.A semidiscrete nonlinear scale-space theory and its relation to the Perona-Malik paradox[C]//Solina F.(Ed.).Advances in computer vision.Wien：Springer,1997.1-10.

[9]Patrick Guidotti.A new nonlocal nonlinear diffusion of image processing[J].Elsevier Inc.J.Differential Equations,2009,246 (12)：4731-4742.

[10]Tikhonov A,Arsenin V.Solutions of Ill-Posed Problem[M].New York：Wiley,1977.87-94.

[11]Leonid Iakov Rudin.Images numerical analysis of singularities and shock filters[J].Caltech,CSTR,1987,5250：87.

[12]Osher S.J,Rudin L.I.Feature-oriented image enhancement using shock filter[J].SIAM J.Num.Anal,1990,27：919-940.

【責任編輯 牛懷崗】

A Comparative Study between P-M and TV Models In Additive White Gaussian Noise Denoising

YANG Qiao,LI Wu-qiang,HAN Guo-dong
(Institute of Mathematics and Information Science,Shaanxi Normal University,Xi'an 710062,China)

Noise is inevitable phenomenon in the process of image acquisition,transmission and storage.As the first step and the basic problem of image processing,denoising is the foundation of subsequent high level image processing.This paper,taking the additive white Gaussian noise as an example,summarizes the principle of the P-M diffusion equation and TV model,and compared the denoising effect from two aspects of visual and quantitative indicators.Finally,under the condition of pretreatment of thermal diffusion equation model,it compared the effect of denoising of the two models.

image denoising;P-M diffusion equation;Total Variation(TV)model;thermal diffusion equation

O175.23

A

1009-5128(2014)15-0005-06

2014-05-29

國家自然科學基金項目：非線性算子方程變號解的局部與全局特性(11101253);中央高校基本科研業務費：非線性算子方程的變號解與分歧(GK201301007)

楊巧(1989—),女,河南鶴壁人,陜西師范大學數學與信息科學學院碩士研究生;韓國棟(1978—),男,山西祁縣人,陜西師范大學數學與信息科學學院副教授,理學博士,主要從事非線性泛函分析及其應用研究.