往復壓縮機管道系統振動計算方法的研究

郭景宏 蘇景武 王芝杰

(1.天華化工機械及自動化研究設計院有限公司；2.青海鹽湖鎂業有限公司)

往復壓縮機主要應用于石油化工、化學化工等領域，但管道振動問題一直存在并影響著往復壓縮機工作性能。通常往復壓縮機共振是振動發生的主要原因，往復式壓縮機周期性吸排氣產生氣流脈動，當管道結構固有頻率、管道內氣柱固有頻率與壓縮機氣流脈動激發頻率接近時，就會引起管道劇烈振動，使管道與其附件的連接部位易發生松動和破裂，威脅裝置的安全運行。

近幾年，國內外對振動的研究工作主要集中在以下幾個方面：完善轉移矩陣，通過數值模擬和實驗[1]，但這些研究主要側重于簡單管道氣柱固有頻率；轉移矩陣是建立在一維數學模型基礎上的，故計算復雜管系氣柱固有頻率時，顯得較為繁瑣且計算值較為粗略[2]。筆者在前人研究的基礎上，用有限元法模擬幾何形狀復雜管道，以某石化廠往復式壓縮機復雜主管道的振動分析為例，通過分析包括三通管、彎頭的管道，得出研究氣柱固有頻率和管道結構固有頻率的計算方法，為識別往復壓縮機管線振動提供了方法和理論依據。

1 基本理論

1.1氣柱固有頻率有限元方程的建立

對于壓縮機管道內氣體，有以下幾點假設：該氣體為無粘性、可壓縮氣體；氣體平均速度、平均壓力和平均密度在該管道方向上是定值；對于該氣體只考慮氣體脈動影響。

壓縮機管道氣柱聲學波動方程可寫為[3]：

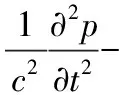
(1)

式中c——聲速；

p——聲壓；

t——時間；

▽——拉普拉斯算子。

通過變換可得壓縮機管道氣柱固有頻率的有限元方程[4]：

(2)

式中 [F]——總載荷列向量；

[Kp]——總剛度矩陣；

[Mp]——總質量矩陣。

由于非對稱矩陣法(UNSYMMETRIC)主要用于求解模型生成的剛度矩陣、質量矩陣不對稱等問題，ANSYS模擬計算中非對稱法是采用完整的[K]和[M]矩陣，計算剛度和質量為非對稱的問題，因此非對稱法對于聲學、流體-結構耦合問題的模擬求解是比較精確的。

1.2管系結構固有頻率和振型向量方程的建立

在機械結構的動力分析中，利用彈性力學有限元方法建立動力學模型，進而計算出結構的固有頻率和模態振型。求解管道結構的固有頻率和振型時，由于阻尼影響較小，可不計阻尼的作用。因此管系的自由振動方程為[4]：

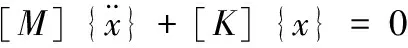
(3)

對n個自由度管系，位移向量為{x} = [x1，x2，x3，…，xn]T，[M]、[K]均為n×n階對稱矩陣。對具有足夠約束的管系，[M]、[K]是正定的。

式(3)是二階常系數齊次微分方程組，設各個位移分量作相同的簡諧振動，即：

{x} = {X} sin(ωt+ψ)

(4)

式中 {X}——振幅向量，{X} = [X1，X2，X3，…，Xn]T；

ω——振動圓頻率。

消去代數因子sin(ωt+ψ)得到方程組為：

([K]-ω2[M]){X} = 0

(5)

式(4)有非零解的充要條件是其特征矩陣行列式為零，即：

det([K]-ω2[M])=0

(6)

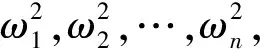
2 計算實例

2.1壓縮機主管道內氣柱固有頻率計算

壓縮機主要介質是聚丙烯，雙作用、排氣壓力2.06MPa、轉速740r/min；管徑φ45mm×3.5mm、φ219mm×5mm、φ16mm×3mm。管道內氣柱選用Fluid30單元，由于氣柱的固有頻率與振幅無關，因此可以把端點不為零的p或u設為1，此管道入口為緩沖罐，視為聲學開口邊界條件，管道與截止閥連接的一端視為聲學上的閉口條件[1]。其ANSYS軟件模型如圖1所示。計算時室內溫度為26℃，根據此溫度查得空氣的密度ρ=1.181kg/m3，聲速c=346m/s。對其進行密度為10的網格劃分，在緩沖器連接管道端施加約束p=0的壓力載荷。選取模態分析類型，用非對稱矩陣法法算出管道內氣柱的前六階固有頻率值見表1。

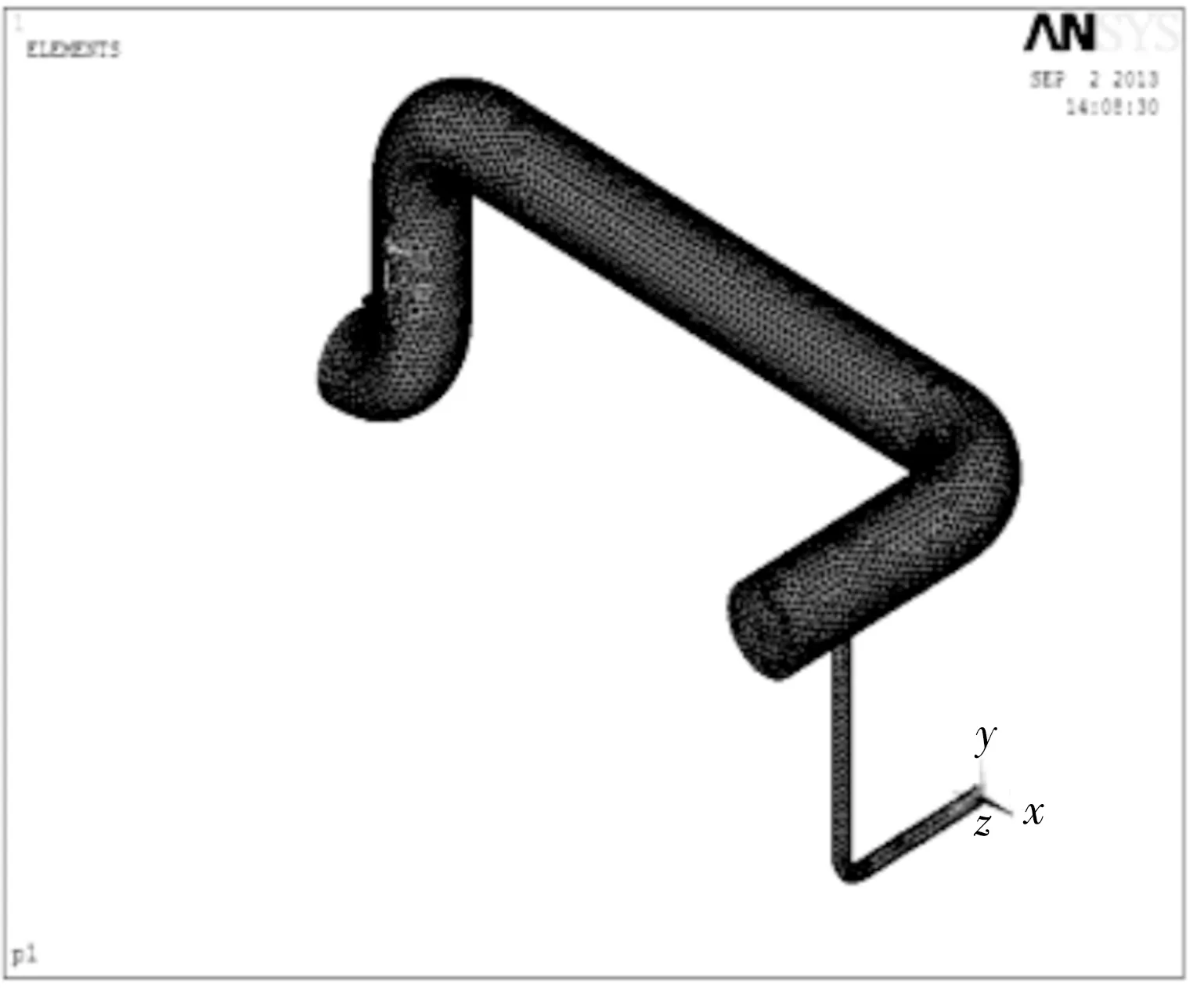
圖1 管道氣柱模型圖

表1 管道氣柱前六階固有頻率值

2.2壓縮機主管道結構固有頻率計算

建模時管系的材料性能常數為：彈性模量E=210GPa，泊松比μ=0.3，密度選用ρ=7800kg/m3。定義的梁單元Beam189對管道模型進行網格劃分的有限元模型如圖2所示，根據現場管支架約束施加邊界條件的有限元模型如圖3所示。選取Modal分析類型，用Block Lanczos法算出管道結構的前六階固有頻率值見表2。對計算結果進行后處理做模態擴展，為了更清楚比較研究，只提取振型變形比較明顯的第四、六階振型圖(圖4)。

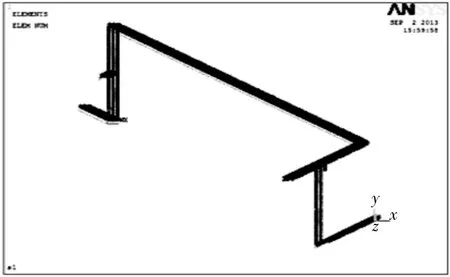
圖2 管系有限元網格模型

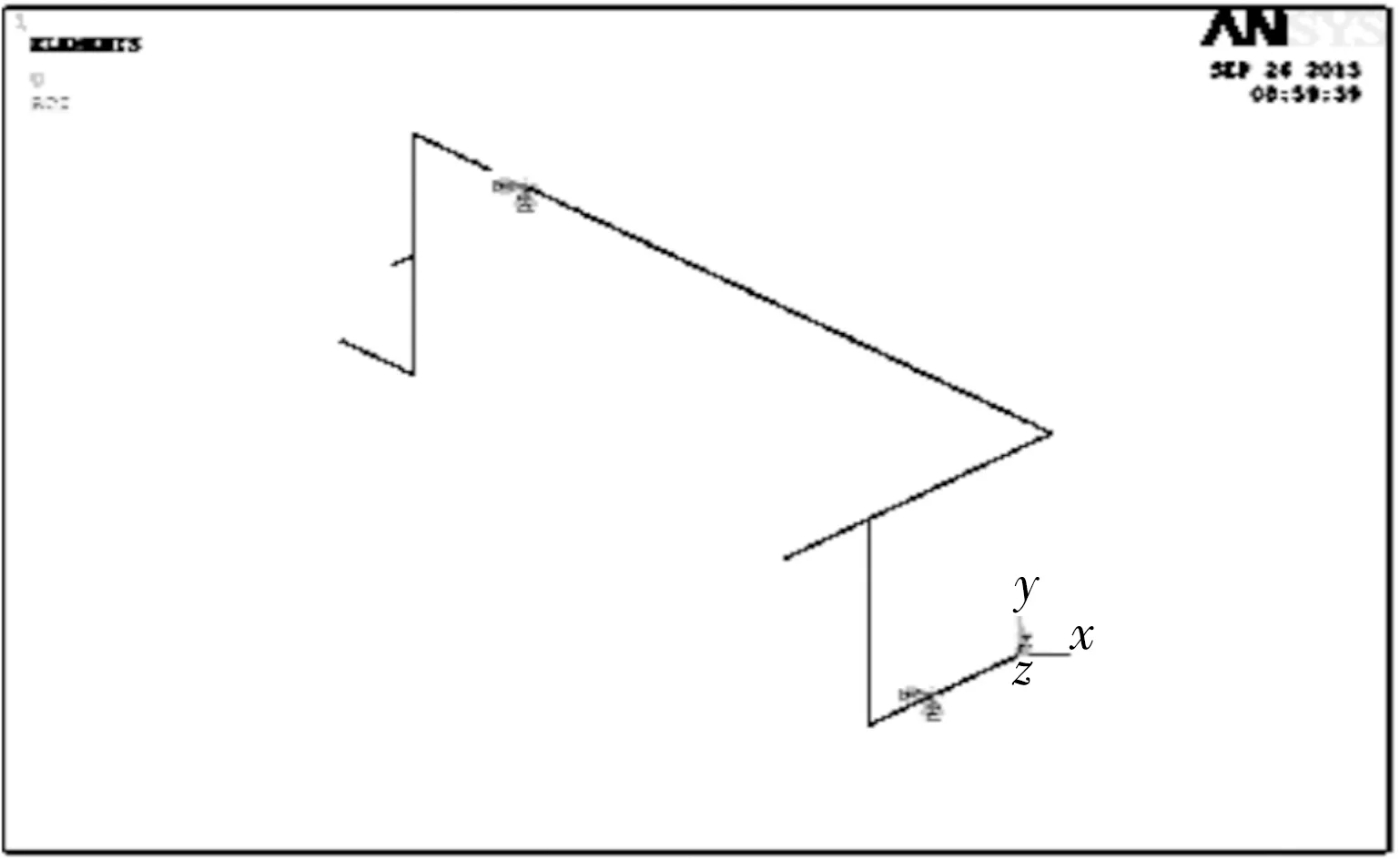
圖3 施加約束管系有限元模型

表2 管道結構前六階固有頻率值

圖4 原管線的固有頻率振型圖

2.3激發主頻率計算

往復式壓縮機激發頻率計算公式為[1]：

式中i——激發頻率的階次，i=1，2，…；

m——壓縮機的作用方式，單作用氣缸m=1，雙作用氣缸m=2；

n——壓縮機的轉速，r/min。

共振區按f=(0.8～1.2)fex計算，該壓縮機的轉速是740r/min，m=2得出前六階激發頻率fex、共振區頻率f見表3。

表3 激發頻率fex和共振區頻率f

3 分析及討論

為了更直觀地研究該往復式壓縮機主管線振動的原因，采用表1～3中的各階頻率作圖(圖5)。

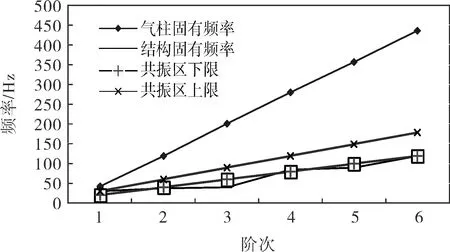
圖5 原管線各階頻率圖

由圖5可觀察到，氣柱固有頻率不在共振區間內，管道結構固有頻率的第一、四、六階固有頻率落在共振區間，且管道結構固有頻率和氣柱固有頻率不接近，所以引起管道振動的主要原因是管道結構固有頻率與激發頻率發生共振產生了激烈的振動。

4 減振措施

為了提高管系的固有頻率，給管線添加更多的約束條件，在靠近彎頭、三通管處加上約束[5]，如圖6所示；計算得出的結構固有頻率值見表4；并觀察新管線的第四、六階振型(圖7)，與原管線振型圖進行比較；最后采用表1、2、4中的各階頻率作圖(圖8)，可以看到減振效果良好。

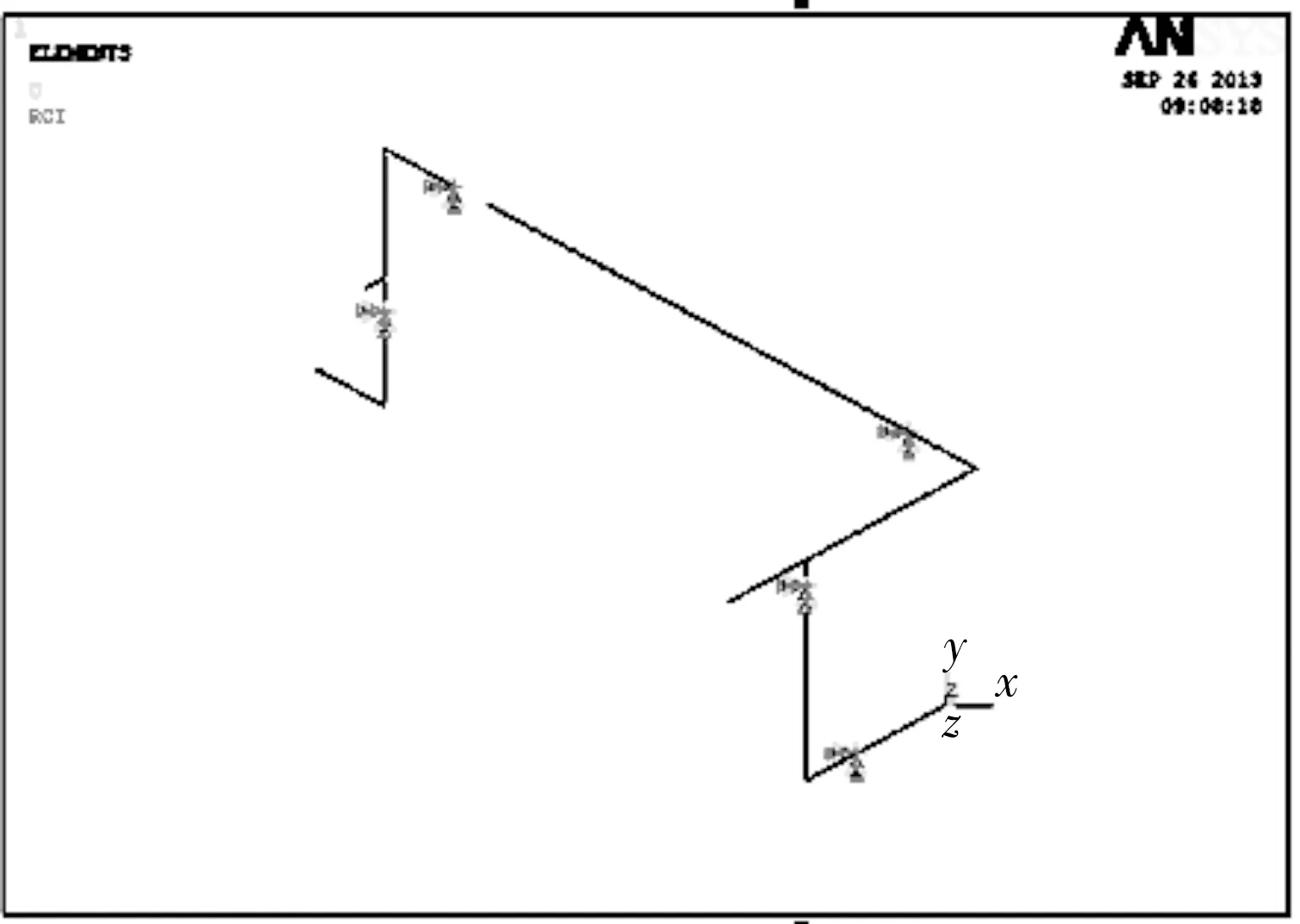
圖6 管系結構有限元模型(增加約束)

表4 施加約束后管道結構前六階固有頻率值

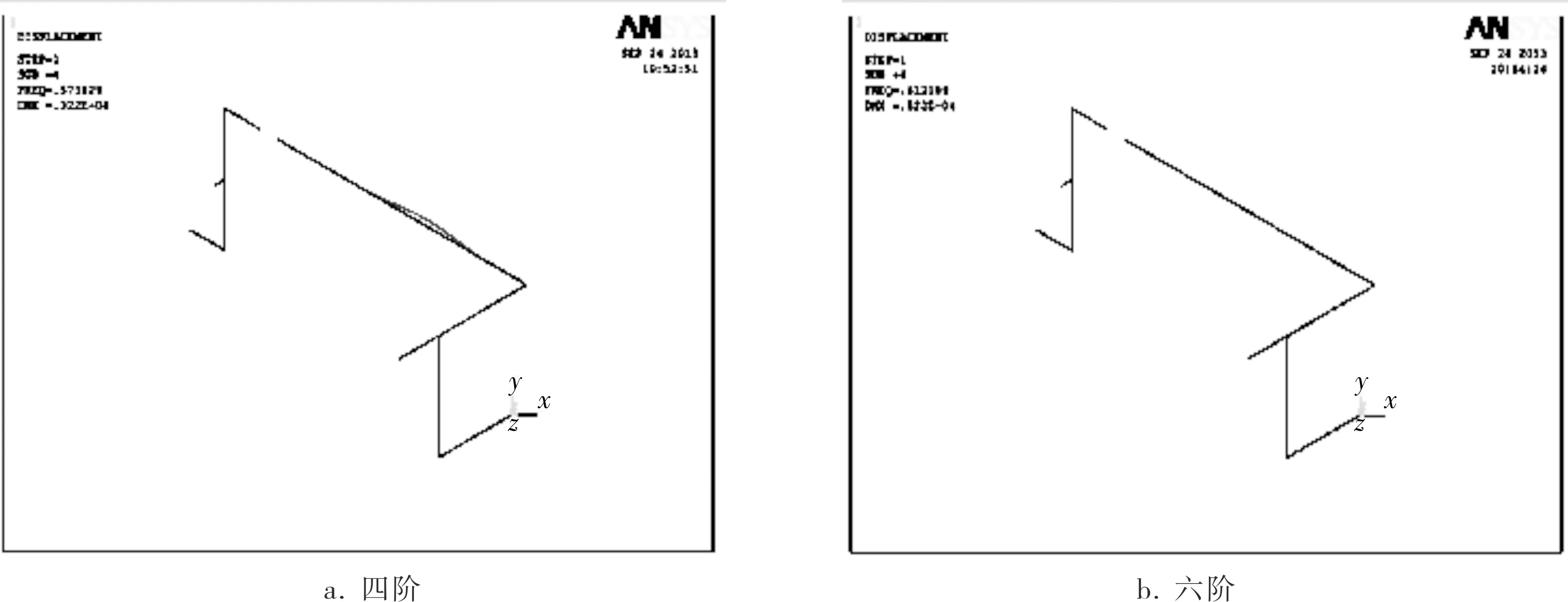
圖7 新管線的固有頻率振型圖

通過施加更多的約束之后，管道固有頻率明顯提高，順利避開了前六階共振區；并且從相應的振型圖上看出第四、六階振動明顯減弱。

5 結論

5.1管道靠近氣缸管段存在彎頭，這樣，較大氣流壓力脈動在轉彎處對管道會產生激振；在現場允許的前提下，盡量減少彎頭，使管路走向明晰。

5.2管道系統支撐太少，管道剛度很低，由于往復壓縮機激發頻率較低，因此管道固有頻率比激發頻率越高越好，至少應該避開前六階共振區，而提高固有頻率的一項有效間接方法是在合適的位置施加相應約束條件，通過新約束，管線結構固有頻率明顯提高，從而順利避開了共振區，消除了由共振引起的振動。

5.3要消除管道激烈振動，首先應該確定振動原因，一般應對管道的氣柱固有頻率、結構固有頻率進行全面、細致的計算，對管道聲學特性和結構特性進行詳細分析。通常實踐中經常遇到的管道振動的主要原因之一是管道共振引起的，筆者提供的計算振動的方法，通過提高結構固有頻率值可以有效避免共振，所采取的措施簡單易行，為實踐中此類問題提供了解決方法和理論基礎。所用ANSYS模態分析是結合了聲學、結構和流體的方法，計算結果與理論計算吻合，為工程中復雜管道振動問題提供了新的計算方法。

[1] 徐斌，馮全科，余小玲.往復壓縮機級間管路氣流脈動研究[J].壓縮機技術，2009，(3)：1～3.

[2] 沈繼忱，趙士榮，董明瑞.管道振動故障三維識別方法[J].化工自動化及儀表，2012，39(1)：28～31.

[3] 黨錫淇，陳守五.活塞式壓縮機氣流脈動與管道振動[M].西安：西安交通大學出版社，1984：7～143.

[4] 姜文全，楊帆，王茂延，等.基于 ANSYS的壓縮機管系結構振動模態分析[J].噪聲與振動控制，2008，28(4)：13～15.

[5] 李思聰，劉智勇，紀燕飛.約束條件對往復式壓縮機管系結構固有頻率的影響[J].化工機械，2012，39(5)：36～38.