大型旋轉機械轉子離心應力有限元分析

0 前 言

組合式轉子具有重量輕、剛度大和易冷卻等諸多優點，被廣泛應用于諸多大型旋轉機械中，是旋轉機械的心臟。然而，組合式轉子結構龐雜，在機組穩態運行過程中，轉子離心作用所產生的應力占總應力50%以上，對機組正常運行提出巨大的挑戰。目前，國內外學者普遍采用有限元法對此類大型轉子的相關問題進行研究，取得了一定的成果。Hamdi T和Blacker T等人運用有限元法計算了轉子的應力集中和臨界轉速；李浦、袁奇等人采用三維有限元非線性接觸算法，計算了拉桿轉子輪盤在預緊力和扭矩作用下的應力分布。

由于本文所涉及的某大型旋轉機械轉子非中心對稱，結構比較復雜，因此需要建立三維模型進行有限元分析。然而，龐大的三維模型不僅需要巨大的計算資源，而且對于計算精度及收斂性也要求頗高。為解決此類大型設備的高效、精確有限元計算問題，本文以某大型旋轉機械轉子離心應力有限元分析為例，基于ABAQUS軟件，闡述了一種先確定整體模型網格單元密度，后采用子模型精確計算局部應力的方法。

1 三維模型特征去除

圖1為某大型旋轉機械轉子三維模型的剖視，圖中，1為轉子左端軸頭、2為左端輪盤、3為左端鼓桶、4為左端拉桿、5為右端鼓桶、6為右端輪盤、7為右端拉桿、8為右端軸頭。

圖1 某大型轉子三維模型剖視圖

由圖1可知，組成該型轉子的零部件較多，所包含的幾何特征更多。過多幾何特征的存在，尤其是微小幾何特征，不僅大幅增加計算量和時耗，而且會帶來計算難以收斂的問題。按照以往計算經驗，微小幾何特征的去除幾乎不會影響計算精度。因此，在進行整體網格劃分之前，對組成轉子的幾個部件進行了特征去除工作，主要包括左端軸頭、左端鼓桶、螺母、右端軸頭、左端拉桿和右端拉桿等部件。圖2a及b分別表示左端軸頭特征去除前后的三維模型，這里將左端軸頭端部凸臺、頂錐孔、端面小孔以及氣封槽等特征去除，其余部件特征去除與之類似，此處不再贅述。在去除微小幾何特征之后，采用ABAQUS軟件對各部件特征去除前后的離心應力進行了驗算，結果兩者應力集中分布幾乎一致，計算精度和計算時間變化情況如表1所示。由表1可知，相比原模型，微小幾何特征去除后各部件離心應力的計算精度下降很小，最大為1.23%，而計算耗時大幅降低，最大為46%，由此說明了特征去除的必要性。

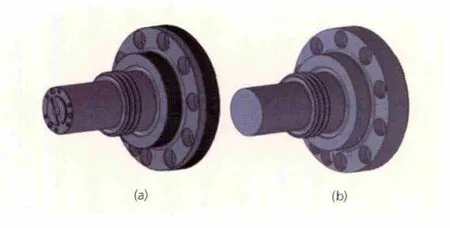
圖2 左端軸頭特征去除

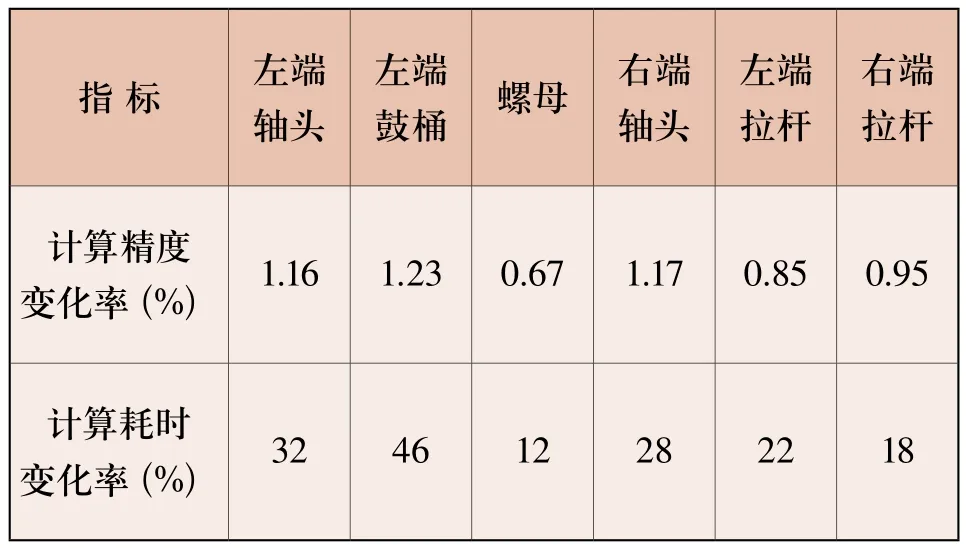
表1 特征去除前后計算效率變化情況

2 有限元建模分析

2.1 邊界條件設置

將特征去除后的三維模型以*.step格式導入ABAQUS軟件，賦予各部件相應的密度、楊氏模量和泊松比等材料屬性；選取靜態通用載荷步，設置好初始載荷步增量；分別在左右兩軸承支承位置對應的轉子軸段外圓面施加位移約束，左側自由度全部約束，右側除軸向平移自由度外，其余的自由度也全部約束。

旋轉的轉子產生離心作用，轉子各部分質量在旋轉過程中受到的離心作用力大小可由式1表示如下：

式中，m表示組成轉子質量塊的質量大小；ω表示轉子旋轉角速度；r表示質量塊與旋轉軸間的距離。由于該型轉子實際工作轉速為6 580r/min即689rad/s，因此可以預測轉子旋轉產生的離心作用將會導致較大的離心應力，這將很不利于轉子的穩定運轉。因此，有必要通過有限元法計算轉子離心應力，以期改進轉子結構，減小應力集中。本文在有限元分析軟件ABAQUS中使用Rotational Body Force即旋轉體力對轉子離心作用加以模擬，通過指定轉子繞x軸的角速度ω=689 rad/s，可將離心作用加載到模型中，如圖3所示。

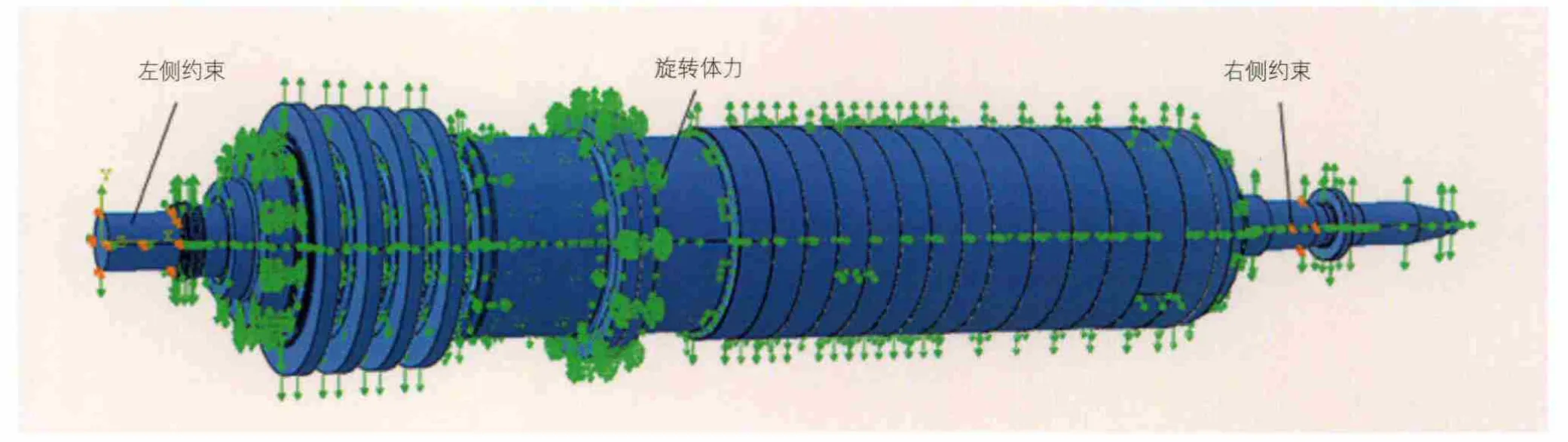
圖3 轉子邊界條件設置

2.2 網格劃分

在給定邊界條件的情況下，離心作用產生的應力大小和分布主要取決于有限單元網格劃分。網格劃分過程中所選擇的網格大小、疏密分布以及單元類型等都會對計算精度產生較大的影響，圖4a為四節點四面體單元，其各節點多項式位移模式如式2所示。

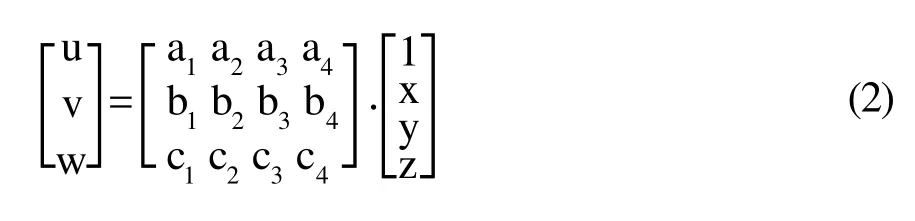
形函數如式3所示：

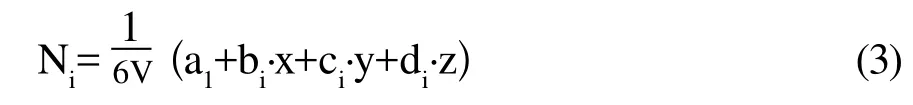
其中，V為體積單元，i=1，2，3，4。圖4b為十節點四面體單元，節點多項式位移模式如式4所示：

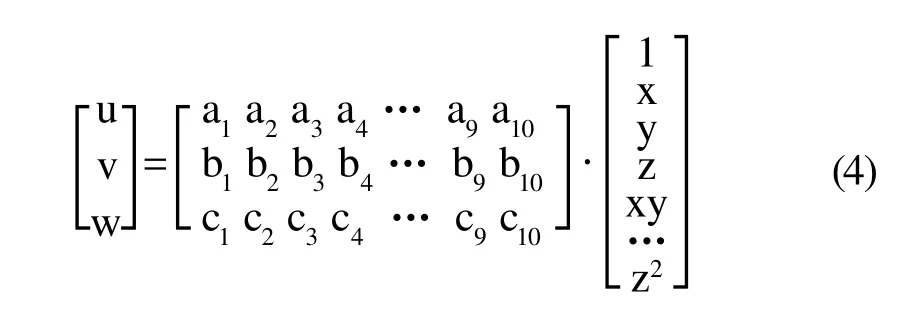
基于自然坐標系的形函數如式5～11所示：

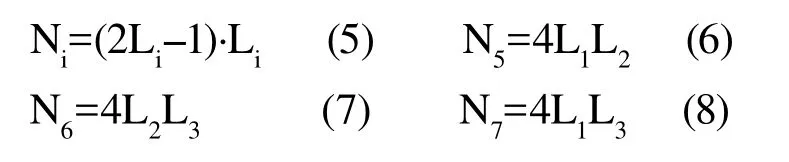
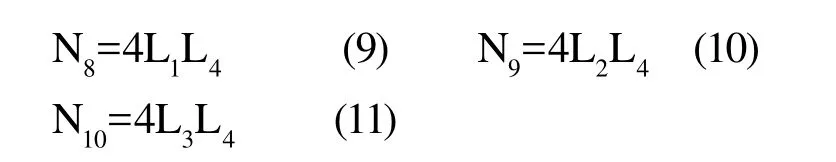
其中，i=1,2,3,4。由此可知，高次位移函數能更好地逼近復雜結構的位移分布，也即高階單元能夠更好地逼近實際結構中曲線和曲面，多項式位移插值函數階數越高，計算精度也就越高。

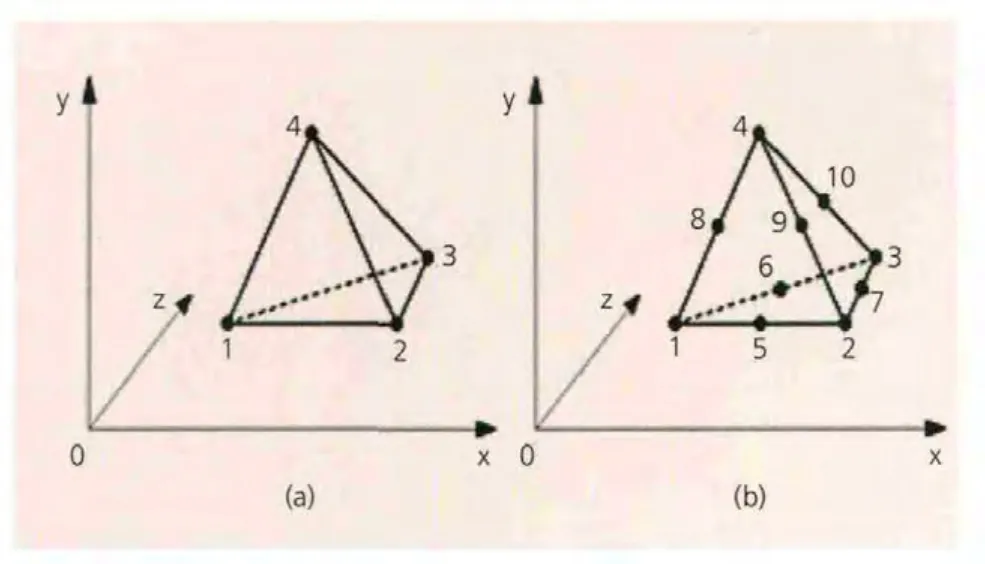
圖4 四面體單元

本文采用如下方法來解決計算精度和計算耗時之間的矛盾：首先對整體轉子進行四面體一階單元網格劃分，按照經驗，確定1.5%為精度指標，以期用最小的計算資源確定合適的網格密度；然后再運用子模型法對所關心的部件進行二階單元重新網格劃分，獲得更加精確的離心應力值。

分別用12號～21號大小的四面體單元種子對同一轉子模型進行網格劃分，得到了十組不同網格數目的有限元模型，以前后兩者最大離心應力相差1.5%為界來選取相對合適的網格密度。當單元種子大小為13號時，計算得到轉子各主要部件離心應力結果云圖如圖5～圖7所示。

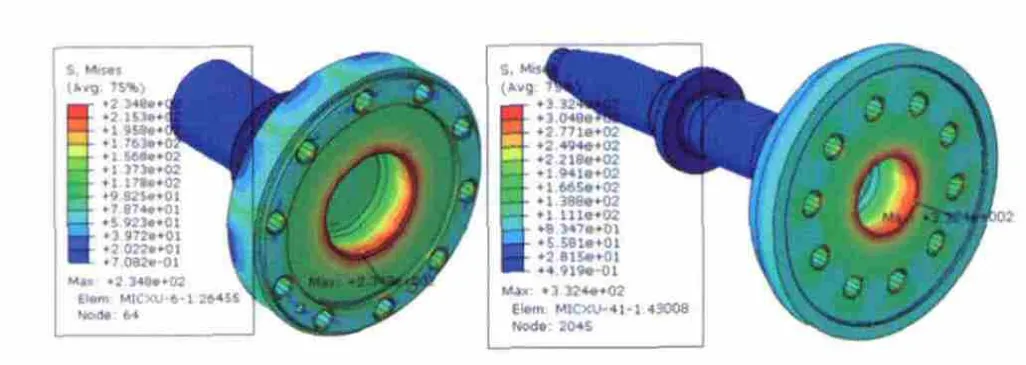
圖5 左端/右端軸頭離心應力分布

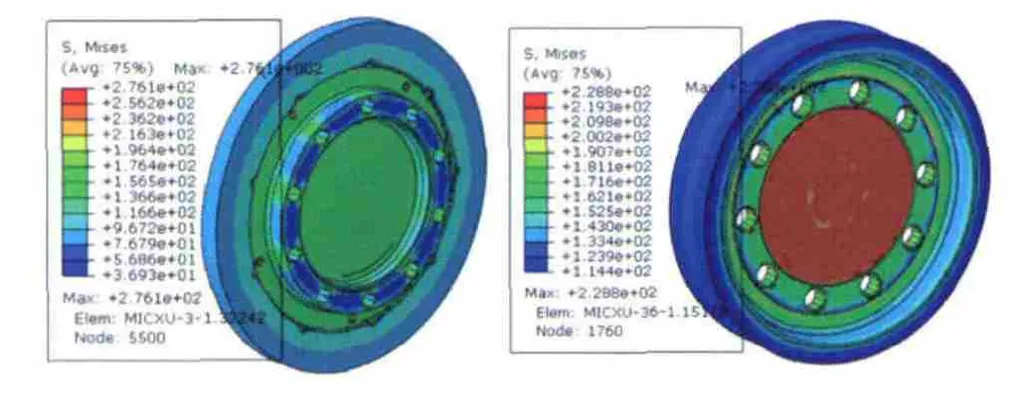
圖6 左端/右端輪盤離心應力分布

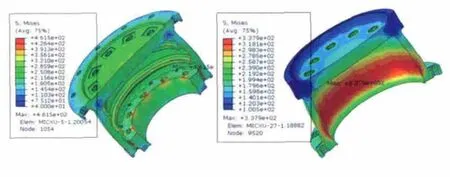
圖7 左端/右鼓桶離心應力分布剖視圖

2.3 結果分析

由圖5～圖7可知，兩端軸頭最大離心應力均出現在內腔邊沿處；左端輪盤最大離心應力出現在冷卻孔邊沿；右端輪盤最大離心應力出現在中部最薄輪輻邊緣；左端鼓桶最大離心應力出現在靠近左端一級輪盤的拉桿孔內沿；右端鼓桶最大離心應力則出現在中部外圓薄壁上。由此可以得到在該轉子旋轉過程中，對離心作用較敏感的位置如下：第一，含有腔體的部件，其腔體邊沿處；第二，盤型部件的薄壁與厚壁接合處；第三，拉桿凸臺與拉桿孔接觸位置。這些結論可為該型轉子的結構設計提供良好的參考。

通過10組不同網格數目的模型計算得到的轉子各部件最大離心應力幾乎分布在同一位置，其中最大應力值出現在左端鼓桶拉桿孔內沿，此處正是集腔體、薄壁和接觸三大離心作用敏感因素于一體的位置，也進一步驗證了前述離心應力分布規律結論的可信度。離心應力大小隨網格數目變化規律如圖8所示。由圖8可以發現，當單元種子為13號即網格數目約為236萬時，前后兩者最大離心應力相差1.3%小于1.5%，已滿足既定要求。由此可以認為整體轉子網格劃分已達最佳，無需再進行網格加密計算。

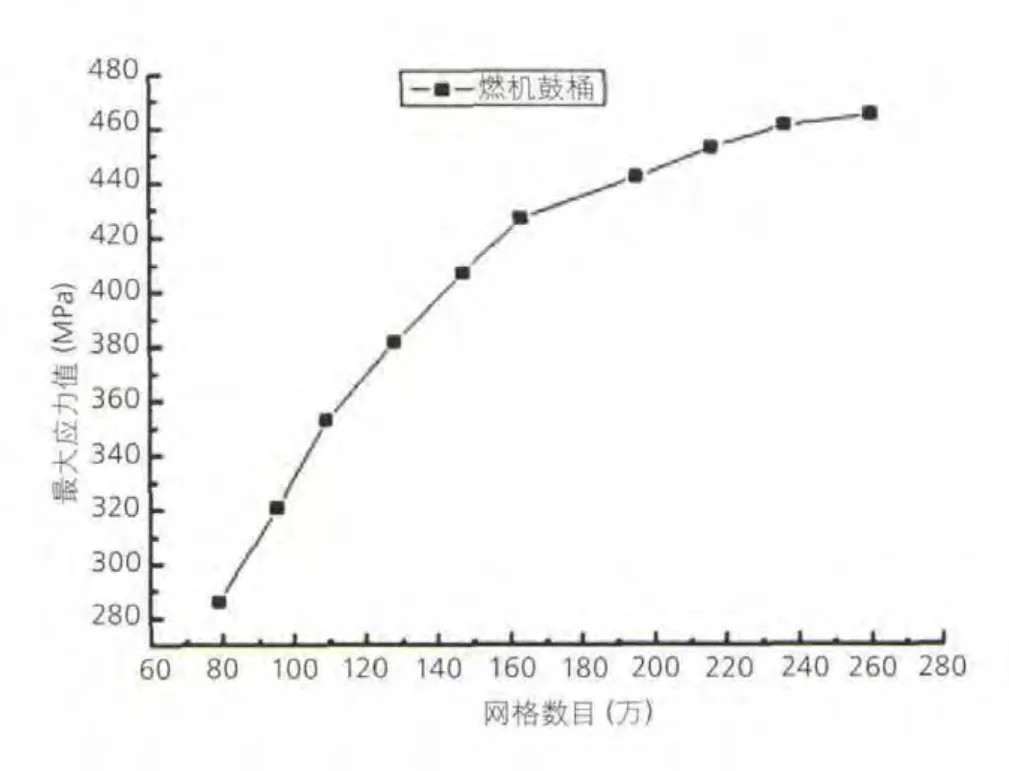
圖8 最大離心應力隨網格數目變化曲線

3 子模型法

通過前文的計算分析，得到了整體轉子較合適的網格數目，可以認為整體網格數目這一因素不會對計算精度造成影響。但是由一階四面體單元計算得到的應力值只能較好地反映該型轉子整體的離心應力分布規律，其應力計算結果偏剛，往往比準確值略小，因此計算精度有待進一步修正。介于此，本文采用基于ABAQUS軟件的子模型法，對其中應力最大的左端鼓桶作進一步的離心應力計算，采用種子號更小的二階單元對其重新進行網格劃分，以期利用較小的計算資源，得到更精確的計算結果。

在完成全局模型計算的基礎上，去除了除左端鼓桶之外的其余轉子組件，將左端鼓桶的兩端面及拉桿孔內表面一起定義為子模型邊界，計算過程中讀入全局模型結果文件作為其邊界條件和驅動變量。圖9為沿軸向依次選取的左端鼓桶軸截面上的21個節點，分別在全局模型和子模型中計算得到的離心應力值。

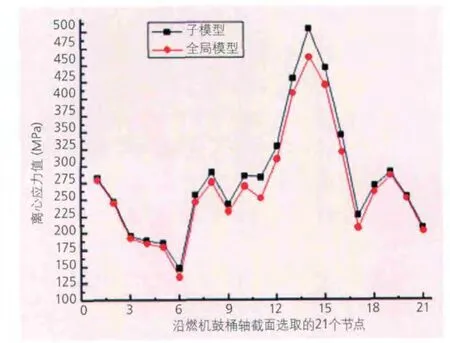
圖9 兩種模型下左端鼓桶節點離心應力值

由圖9可以發現，子模型法計算得到的左端鼓桶各節點離心應力分布規律基本與全局模型類似，并且離心應力值比全局模型中略高；全局模型中左端鼓桶最大應力為461MPa，小于子模型中的504MPa；最大應力都發在14號節點即鼓桶靠近左端第一級輪盤的拉桿孔內沿。由于在子模型中運用了節點數更多的二階單元，并且單元種子號更小，因此有理由認為離心應力計算值更加精確。子模型與全局模型的離心應力有限元分析效率如表2所示，由此可以看出子模型法不僅計算精度頗高，而且計算耗時可大幅減少。該型轉子其余部件子模型法計算過程與此類似，此處不再贅述。

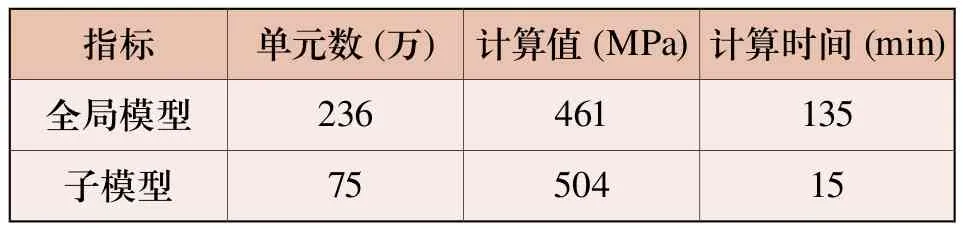
表2 子模型與全局模型計算效率比較

4 結 論

為解決大型復雜結構精確、高效的有限元計算問題，本文以某大型旋轉機械轉子離心應力有限元分析為例，采用全局模型確定網格密度、子模型計算最終結果的方法，得到主要結論如下：

(1)對整個轉子而言，離心應力最大位置在轉子中部鼓桶上；對各組成部件而言，應力集中主要發生在含腔體、薄壁和接觸等因素的位置；

(2)為確定大型復雜三維模型合適的有限元網格密度，可以通過某一精度指標，以較粗略的有限單元進行多次網格劃分，從而得到滿足指標的最經濟的網格數目；

(3)相比全局模型，子模型法計算易收斂，效率高，精度好，非常適合旋轉機械轉子等大型結構的有限元計算。

[1]劉恒，陳麗.周向均布拉桿柔性組合轉子軸承系統的非線性動力特性[J].機械工程學報 2010，46（19）：53-62.

[2]何鵬.分布式拉桿轉子動力學特性分析[D].哈爾濱：哈爾濱工業大學，2009.

[3]杜世淵，閻淑麗.高速轉子離心力及其效應的仿真與分析[J].機械管理開發，2010, 25(6)：201-202.

[4]王俊瑜，紀冬梅，姚秀平，等.汽輪機啟動過程中轉子應力的主要影響因素[J].上海電力學院學報，2012,28(3)：238-246.

[5]Hamdi T，Mehmet P.Evaluation of gas turbine rotor dynamic analysis using finite element method[J].Measurement, 2012，45(5)：1089-1097.

[6]Blacker T.Automated conformal hexahedral meshing constraints，challenges and opportunities[J].Engineering with computers，2001,17(3)：201-210.

[7]李浦，袁奇，高進，等.周向拉桿轉子輪盤端面齒接觸應力分析[J].熱力透平，2013, 42(1)：25-29.

[8]Tomislav S，Anica T, Kristian L.Parametric study of operating and geometry characteristics effect on heat transfer in annular finned tube heat exchanger[J].Eng.Rev，2009，29(1)：25-36.

[9]高素荷，姚河省.網格劃分密度和有限元求解精度研究[C]/第三屆中國CAE工程分析技術年會論文集.大連，2007：480-485.

[10]石亦平，周玉蓉.ABAQUS有限元分析實例講解[M].北京：機械工業出版社，2006：60-61.