起重機械金屬結構疲勞裂紋擴展壽命的估計

荊登峰，周利東

（1.太原城市職業技術學院，山西 太原 030027；2.太原科技大學機械工程學院山西太原030024）

起重機械金屬結構疲勞裂紋擴展壽命的估計

荊登峰1，周利東2

（1.太原城市職業技術學院，山西 太原 030027；2.太原科技大學機械工程學院山西太原030024）

針對起重機械結構巨大，疲勞裂紋擴展過程復雜，基于概率斷裂理論，提出了將疲勞裂紋擴展分為表面裂紋、中心穿透型裂紋和邊緣穿透型裂紋三個階段的數學模型，通過Monte-Carlo數值模擬，得出了裂紋擴展各個階段的時間在總壽命中所占比例，研究表明在板厚達到0.012米以上時才可忽略中心裂紋和邊緣裂紋的影響，研究結果可為重型機械在變幅及隨機疲勞載荷下剩余壽命的估計奠定理論基礎。

起重機械；裂紋擴展；疲勞壽命

一、應用背景

起重機械由于疲勞斷裂而造成的事故越來越多，一旦發生就會造成嚴重的后果，需要精確地預估出其金屬結構剩余疲勞壽命。當前多是采用斷裂力學和疲勞累積損傷理論來預測剩余壽命，在裂紋擴展模型上有使用穿透型裂紋和表面裂紋。但是，由于起重機械金屬結構巨大，使用單一的裂紋擴展模型難以準確地評估出剩余壽命，往往得到偏于保守的結果，為解決這一問題，本文提出了一種裂紋擴展分三個階段：表面裂紋、中心穿透型裂紋和邊緣穿透型裂紋的剩余壽命計算模型，并對參數的選擇問題上進行了有益的討論。

二、焊接箱型梁的疲勞裂紋擴展機理和計算模型

根據已有起重機箱型梁疲勞試驗數據，可以看出裂紋擴展導致破壞主要在主梁跨中附近橫隔板-腹板焊趾缺陷起源的裂紋擴展[1]，缺陷起源及擴展的軌跡如圖1。

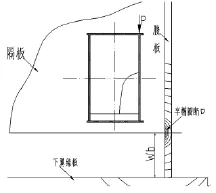
圖1 橫隔板—腹板焊趾缺陷起源的裂紋擴展示意圖

裂紋擴展歷程為：裂紋起源于橫向隔板—腹板焊趾（焊縫與腹板的熔合線）處，為表面半橢圓源點，并從源點穿透腹板厚度。當穿透了腹板厚度后，就以兩端穿透裂紋繼續擴展，一端向腹板上端延伸，另一端走向受拉翼緣。此后擴展速率加快，當下端裂紋進入翼緣焊縫時，上下兩端裂紋擴展均減慢，直至下翼緣板穿透，此時裂紋呈現出橫貫下蓋板的三端裂紋，另一端進一步向腹板上端延伸。隨后上下裂紋擴展進一步加快直至破壞。

由腹板裂紋擴展歷程可見，裂紋擴展過程復雜，本文認為，腹板裂紋擴展過程可能會經歷三個階段：表面裂紋、中心穿透型裂紋和邊緣穿透型裂紋。

1.表面裂紋

第一階段為表面裂紋擴展，也即穿透前的擴展，按照半橢圓的二維裂紋模型進行分析，沿裂紋深度和長度兩個方向擴展，裂紋深度的極限尺寸為腹板板厚。

疲勞裂紋擴展在一定范圍內，兩自由度半橢圓裂紋（如圖2）在常幅載荷下的疲勞裂紋擴展可以通過Paris方程建模。

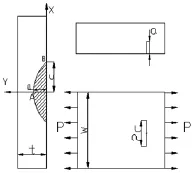
圖2 兩自由度半橢圓裂紋示意圖

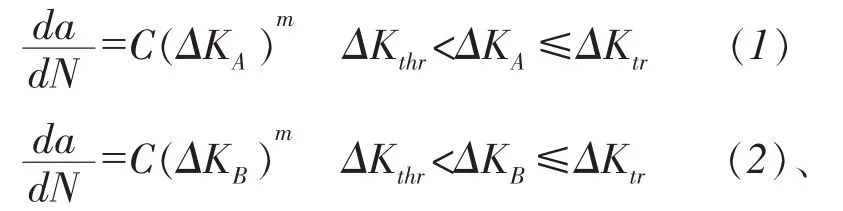
式中a，c是表面裂紋的深度和長度的一半，t和W分別是板厚和板寬，單位都為m，N是施加循環周期數，C，m是Paris參數，ΔKA，ΔKB是裂紋尖端A點和表面點B（圖2）的應力強度因子幅，單位，其Newman-Raju經驗公式為

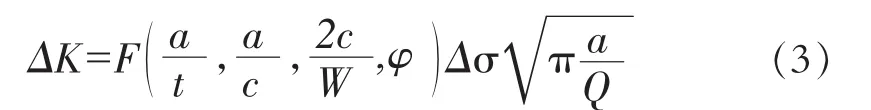
式中，應力范圍Δ=σmax-σmin。Q為橢圓積分因子，為應力修正系數。各個參數的計算可通過查詢手冊得到。Newman-Raju公式形式簡單，通過編程可以快速計算得到裂紋前沿的應力強度因子。

另外，考慮到表面裂紋形狀的不斷變化，假設裂紋擴展的A和B兩點發生在同一區域，可以通過式（2）除以式（1）的方式獲得求解裂紋形狀a/c的差分方程

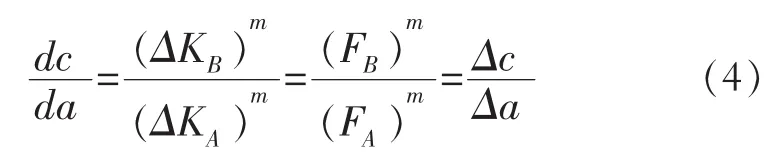
2.中心穿透型裂紋和邊緣穿透型裂紋

第二階段為中心穿透型裂紋擴展。若第一階段表面裂紋深度等于板厚時，結構還沒被破壞就進入該階段。裂紋一旦貫穿，在背表面上，其擴展很快，尤其是橢圓的裂紋形狀，因而表面裂紋前后表面較快拉平，故可看作是中心穿透型裂紋。該階段裂紋的初始尺寸為第一階段裂紋長度的最終值，裂紋的最后尺寸可能是中心裂紋的臨界尺寸，也可能是裂紋源到受拉翼緣板的距離Wb。

第三階段為邊緣穿透型裂紋擴展。若經歷了中心裂紋階段后，結構仍沒有被破壞，就進入該階段，向上擴展。裂紋的最后尺寸是邊緣裂紋的臨界尺寸，這是因為一般裂紋源到腹板中性層的距離大于到受拉翼緣板的距離。

這兩種裂紋類型的計算模型仍選用Pairs法則套用式（1），此時的a，在中心裂紋模型中為裂紋長度的一半，在邊緣裂紋模型中為裂紋長度。應力強度因子幅的計算如下：

3.預估總壽命

在一般情況下，裂紋增長可以由線性Paris法表示，見式（1）、（2）、（5）和（6）。本文提出的裂紋擴展分為三個階段的疲勞壽命計算式子如下：

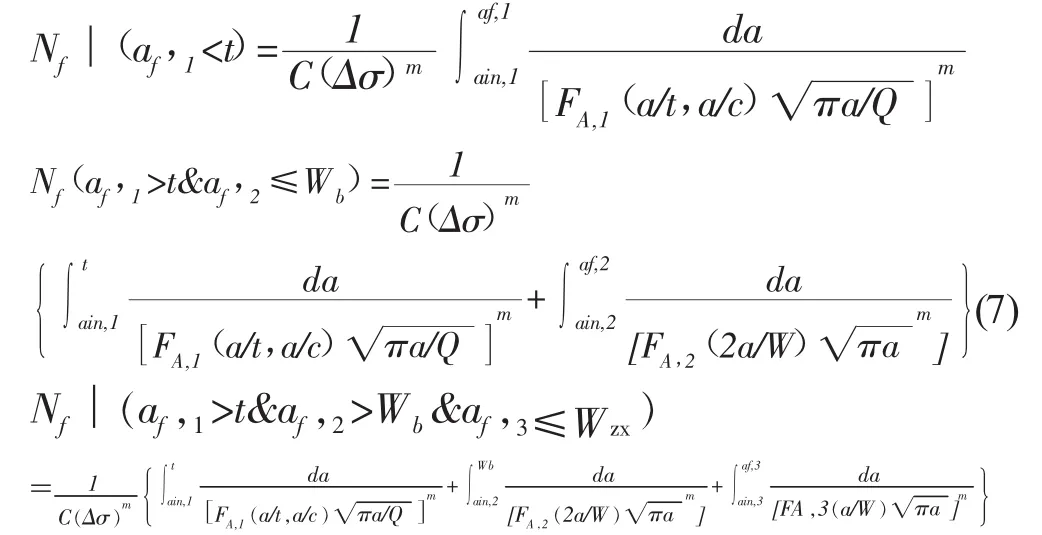
式（7）的第一部分表明，如果表面半橢圓型裂紋的臨界深度af，1小于板厚，那么疲勞壽命是可利用Newman-Raju經驗公式積分計算得到，裂紋從初始深度ain,1=a0到臨界深度af，1增長。

式（7）的第二部分指出，如果表面半橢圓型裂紋的臨界深度af，1大于板厚t，裂紋首先從板厚方向和板寬方向擴展，擴展壽命是裂紋深度從ain,1=cf,1到af，2增長的周期數。然后裂紋擴展模型轉變為中心穿透型，裂紋長度從到增長。

式（7）的第三部分表明，如果裂紋經歷了表面裂紋和中心裂紋，尖端到達受拉翼緣板后仍沒被破壞，也即af，2＞Wb，那么最后還要經歷邊緣裂紋擴展階段，所以總壽命還需加上邊緣裂紋長度從ain,3=2af,2到af,3增長的周期數。

臨界裂紋尺寸由材料的斷裂韌性計算得到

4.隨機變量分布的確定

考慮到本文的研究情況，確定性的變量是板厚（t=3，6，8，10×10-3）和板寬（W=1.5米）（見圖2）。當前的研究中，一般假定Paris指數m是確定的值。本文取m=2.735829[8]錯誤！未指定書簽。。所用的其他變量描述如下。

（1）Paris參數C

在以往的許多研究中Pairs參數C服從對數正態分布[5,9,10]，對于在空氣中運行的材料為Q235的起重機械金屬結構，并且按照本文所使用單位，應力強度因子為N· m-3/2和裂紋尺寸為 m，那么參數C的期望值為μC=1.83×10-13×10（3-3m/2）=1.4411×10-14，變異系數取為0.54[9]。

（2）初始裂紋尺寸

在起重機械焊接結構中，存在多種引起缺陷的因素，在擴展階段的裂紋初始深度a0和初始縱橫比（a/c）0對最終壽命的評估有著很大的影響，這兩個變量都被認為是隨機的，本文取為對數正態分布，期望和變異系數分別為（0.1×10-13,0.2）和（0.1,0.2）。

（3）斷裂韌性KC

斷裂韌性KC是材料的一種屬性，與板厚以及實驗條件等因素有關，一般認為是隨機變量，且通過式（8）決定了臨界裂紋尺寸的隨機性，本文取KC服從威布爾分布[11]，期望和變異系數分別為和0.25。

三、數值模擬

應用Matlab應用軟件編寫程序，采用蒙特卡羅方法模擬起重機械有缺陷金屬結構的等幅應力疲勞裂紋擴展過程及其剩余壽命的估計。

1.數值模擬方法

給定板厚t，板寬W和Pairs指數m等參數，計算應力水平S下的疲勞剩余壽命。各個輸入隨機變量的分布上節已述，列于表1，隨機抽樣創建輸入隨機向量；疲勞剩余壽命的估計的計算過程按照裂紋擴展的三個階段進行，流程見圖4，求解式（7）n次，得到疲勞壽命的統計值，在每一次模擬中，計算表面裂紋擴展時間占總壽命的比例。

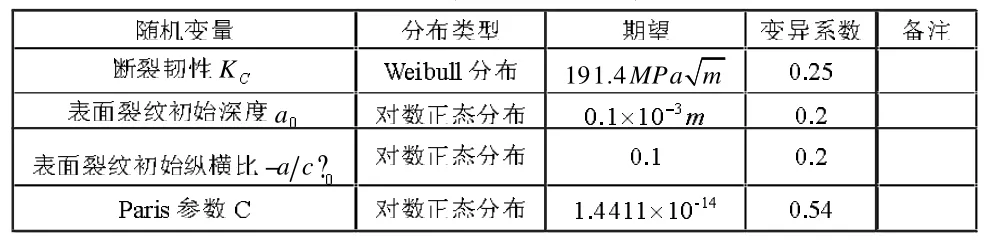
表1 隨機變量分布表

2.數值模擬結果

（1）疲勞裂紋擴展歷程

按照流程圖3，計算給定應力水平，板厚時的疲勞裂紋擴展歷程（見圖4），可以發現在表面裂紋穿透腹板厚度以后，擴展速度相當的快，所以裂紋源到受拉翼緣板的距離對總疲勞壽命有一定的影響，本文取Wb=50×10-3米。

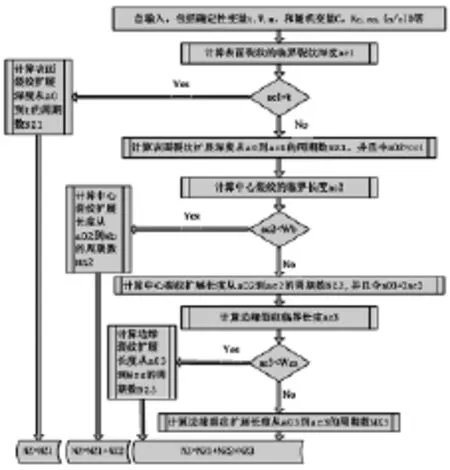
圖3 裂紋擴展三階段模擬流程圖

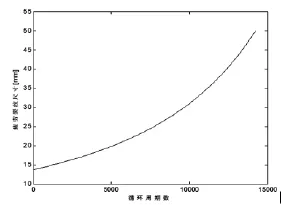
圖4 板厚裂紋擴展歷程

（2）表面裂紋擴展時間所占比例

以往的研究表明，表面裂紋擴展壽命占有總擴展壽命的很大比例，但是具體比例值沒有明確給出。初始裂紋尺寸一定，各輸入隨機變量如表1，不同板厚t，表面裂紋擴展壽命所占比例的平均值，如附表1所示。可以看出，盡管所占比例與應力水平有一定關系，但影響程度遠小于板厚，隨著板厚的增加，所占比增大，在腹板厚為3×10-3米時，僅占83%左右，遠小于95%，但是在腹板厚度達到米以上時，表面裂紋擴展時間占據非常大的比例，那么可以認為，腹板一旦穿透即達到疲勞破壞，中心裂紋及邊緣裂紋擴展時間可不計。

四、結論

（1）起重機械疲勞裂紋擴展，按照表面裂紋、中心穿透裂紋和邊緣穿透裂紋三階段進行剩余壽命評估，具有一定的合理性和可行性。所得恒幅載荷下疲勞壽命數值模擬結果基本符合前期疲勞試驗的結果。

（2）總疲勞剩余壽命中表面裂紋的擴展時間占有很大比例，并且與板厚有很大關系，所以在進行疲勞檢測時需特別注意裂紋是否穿透，及其穿透時間，后兩個階段擴展速度非常快，在較大板厚時才可以忽略不計。

另外，初始裂紋分布依賴于焊接過程和操作員技術水平，它們受制于很多不確定因素，還需要大量的實驗工作以確定其分布。三個階段裂紋擴展使用同樣的Pairs參數和應力水平，有待進一步的驗證。

[1]翟甲昌，王生，申增元，等.橋式起重機焊接箱形梁的疲勞試驗[J].起重運輸機械，1994（2）:3-8.

[2]徐格寧，左斌.起重機結構疲勞剩余壽命評估方法研究[J].中國安全科學學報，2007，17（3）:126-130.

[3]Zhang Y,Taylor D.Sheet thickness effect of spot welds based on crack propagation[J].Engineering Fracture Mechanics.2000，67（1）:55-63.

[4]涂周杰.表面裂紋疲勞擴展和應力強度因子研究[D].武漢:華中科技大學，2006.

[5]涂善東，戴樹和.表面裂紋貫穿板厚后的疲勞擴展行為[J].壓力容器，1990（2）:10-14.

[6]趙章焰，雷新華，孫國正.Q235鋼裂紋擴展參數的實驗測定[J].武漢理工大學學報，2003，25（1）:49-51.

[7]Righiniotis T D,Chryssanthopoulos M K.Fatigue and fracture simulation of welded bridge details through a bi-linear crack growth law[J].Structural Safety，2004，26 (2):141-158.

[8]Righiniotis T D,Chryssanthopoulos M K.Probabilistic fatigue analysis under constant amplitude loading[J]. Journal of Constructional Steel Research，2003，59（7）: 867-886.

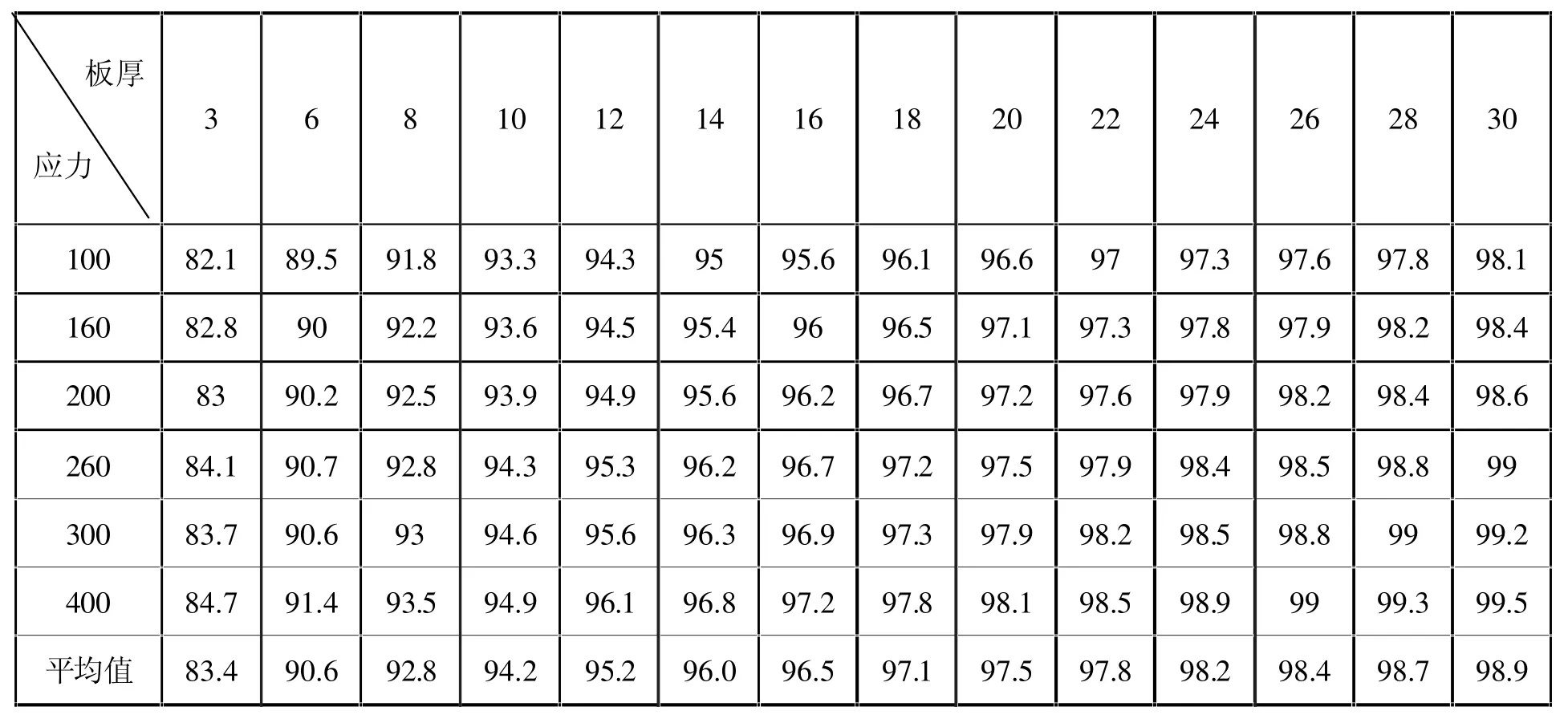
附表1 工作應力幅200MPa時板厚與表面裂紋擴展所占百分比表（板厚t單位，應力也即應力范圍單位MPa）

TH12

A

1673-0046（2014）3-0180-03

太原科技大學博士啟動基金（20122034）