基于改進的模糊數學評價法的外秦淮河水質評價

童朝鋒,呂立銳,馮 騫,邵宇陽

(1.河海大學水文水資源與水利工程科學國家重點實驗室,江蘇南京 210098;

2.河海大學港口海岸與近海工程學院,江蘇南京 210098;3.河海大學環境學院,江蘇南京 210098)

基于改進的模糊數學評價法的外秦淮河水質評價

童朝鋒1,2,呂立銳2,馮 騫3,邵宇陽2

(1.河海大學水文水資源與水利工程科學國家重點實驗室,江蘇南京 210098;

2.河海大學港口海岸與近海工程學院,江蘇南京 210098;3.河海大學環境學院,江蘇南京 210098)

針對河流水質評價中存在的不確定性和模糊性,采用改進的模糊數學評價法,對南京市外秦淮河進行綜合水質評價。結果表明,除七橋甕斷面外,外秦淮河大部分河段水質處于劣Ⅴ類標準水平,其中NH3-N和TP是外秦淮河水質的主要影響因子。

水質評價；改進的模糊數學評價法；單因子評價法；NH3-N；TP

河流水質評價以水環境監測資料為基礎,按照評價目標選擇一定的水質參數、水質標準和評價法,對水體質量進行定性或定量評定,以準確反映水質現狀,了解和掌握水體污染影響程度和發展趨勢,為水環境保護和水資源管理規劃提供科學依據。鑒于水質監測數據量大,不確定性大,且不存在明顯的規律,用于水質評價的方法主要是以統計學方法為主的不確定性方法[1]。應用較多的有單因子評價法[2]、綜合污染指數法[3]、模糊數學評價法、灰色系統評價法[4]、物元法[5]、人工神經網絡法[6]、層次分析法[7]、主成分分析法[8-9]等;此外還有投影尋蹤技術、集對分析和粗集理論、蟻群算法等方法。這些方法考慮了數據的不充分性和水環境決策本身具有的模糊概念等特點,切合我國目前的水環境監測和水質標準的現狀,但是各種方法自身也存在一些問題。單因子指數法評價過于保守,污染指數法不能判斷綜合水質類別,模糊數學法、灰色系統評價法、物元法、層次分析法、人工神經網絡法不能評價劣Ⅴ類水。于是對各種方法的綜合運用,取長補短或者對現有方法進行改進和修正成為主流。隨著統計學原理的發展和應用,產生了綜合水質標識指數法[10]、改進的模糊數學評價法[10]、改進的模糊物元法[11]、層序聚類分析和哈斯圖等方法。其中改進的模糊數學評價法對評價標準進行改進,用每個水質指標上下限值的中間值作為評價標準,從而可以評價劣Ⅴ類水。因此,筆者在對外秦淮河水質評價中采用改進的模糊數學評價法,并對形成這樣評價結果的主要影響因子進行討論。

1 研究區域概況

水質監測斷面位于外秦淮河城區段,屬于外秦淮河下游,是南京市的“母親河”。外秦淮河流域面積2631 km2,流域呈蒲扇形,長寬各50 km左右,丘陵山區占流域面積80%,地勢周高中低。秦淮河有南北兩源,北源稱句容河,南源稱溧水河。句容河沿途有湯水河、解溪河、索墅河等支河匯入,至江寧縣西北村匯入秦淮河干流。外秦淮河城區段跨越秦淮、雨花、建鄴、鼓樓4個區,在南京城南繞行,上游起于運糧河口,經長干橋后匯合落馬澗,在西水關外與內秦淮河匯合,合流后經草場門、定淮門于三汊河口匯入長江,全長15.6km(圖1)。外秦淮河枯水期通過秦淮新河閘抽引長江水進入秦淮新河及外秦淮河,汛期主要靠上游匯流及石臼湖自流進入秦淮河干流及外秦淮河,城區沿程有內秦淮河中段、南段等匯入。

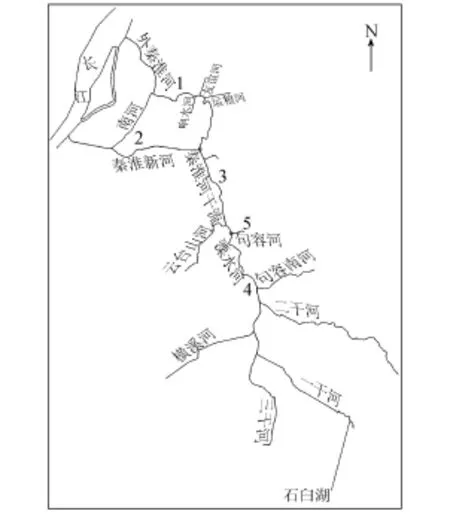
圖1 秦淮河流域水系

2 數據來源

根據外秦淮河的自然條件和功能區水質保護目標要求,在外秦淮河上布置了6個監測斷面(圖2),從上游到下游依次為七橋甕、武定門、鳳臺橋、三山橋、草場門橋、三汊河口。監控指標共有7個：透明度、pH值、DO、NH3-N、CODMn、COD和TP,監測時間為2009年,每月監測4～5次,分析方法選用GB3838—2002《地表水環境質量標準》中規定的基本項目分析方法。根據水質評價參數選擇的針對性和適度原則,主要考慮DO、NH3-N、CODMn、COD和TP等5項指標,以每月水質監測指標的平均值作為分析基礎。監測斷面的數據變化過程見圖3。

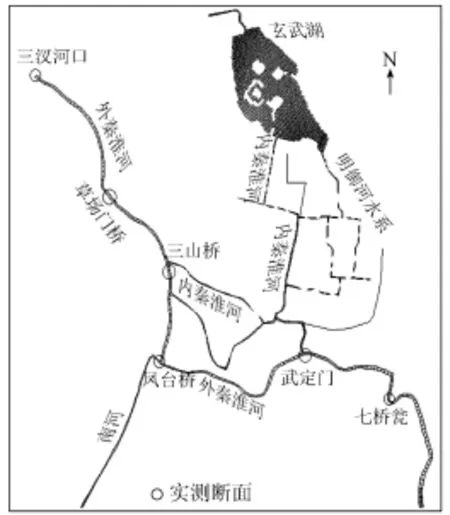
圖2 外秦淮河流域及實測斷面

3 評價法

模糊數學評價法是以模糊數學為基礎,應用模糊關系合成的原理,將一些邊界不清、不易定量的因素定量化,從而進行綜合評價的方法。該方法可以有效得到河道各斷面綜合水質狀況,但是不容易明顯看出對水體水質起主要作用的水質指標,故結合單因子評價法,發揮它可以確定主要影響因子的優點來確定占主要影響地位的水質指標。

3.1 改進的模糊數學評價法

河流水質指標具有總體的不均勻性和局部范圍的相對穩定性,水質污染程度是一個模糊的概念,模糊數學評價根據水功能區相應的水質標準和實測值,經過模糊變換,對水功能區給出客觀、定量的評價。傳統的模糊評價法不能有效地評價劣Ⅴ類水,需要進行一定的改進。評價過程中,找出影響水質的主要因素,確定因子集、評價集、隸屬函數,計算各因子的權重和隸屬度,得到綜合隸屬度,判定該水功能區水質級別。

3.1.1 因子集和評價集建立

選取水質監測的若干指標作為評價因子,建立因子集。在外秦淮河的各監測指標中,選擇DO、NH3-N、CODMn、COD以及TP作為評價因子,則評價因子集U={DO,NH3-N,ρCODMn,COD,TP}。GB3838—2002《地表水環境質量標準》中,將水質分為5個級別,據此確定評價集為V={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。考慮南京市相關部門規劃,外秦淮河城區段水功能區劃為Ⅳ類,那么評價中各指標的最低限值為Ⅳ類水標準值。

3.1.2 建立評價矩陣

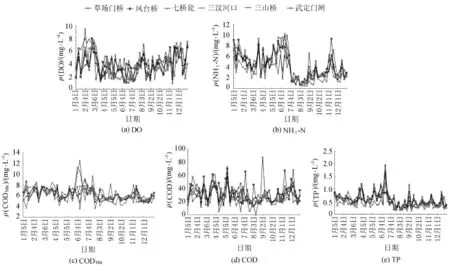
圖3 外秦淮河6個監測斷面5個評價指標實測數據變化

評價矩陣R由上述5個評價因子隸屬于6個不同級別的隸屬度構成,隸屬度根據隸屬函數計算得出。每個因子都有對應于5個級別的隸屬函數：

第1級別：

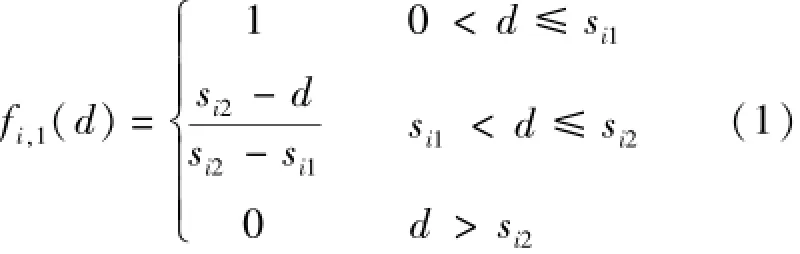
第2～(k-1)級別：

第k級別：

式中：fi,k(d)為隸屬函數;Si,k為第i(i=1,2,…,5)個評價因子的第k(k=1,2,…,6)級水質評價標準;d為各評價因子的實測值。對于DO,基本表達式不變,只需在表達式前加負號。

傳統的模糊數學評價法是將水質各級別標準作為評價標準,這樣就有5個隸屬函數。但這樣做的缺點是不能評價劣Ⅴ類水,最差是評為Ⅴ類水,對于因某些因子超標嚴重造成的水質降低不能有效反映出來,改進的模糊數學評價法體現在對各級別評價標準的確定上,以各級別水質標準上下限的中間值作為準則求取隸屬度,這樣構成6個隸屬函數,從而可以解決不能評價劣Ⅴ類水的問題。例如CODMn指數,按照各級別水質標準,其水質級別區間為(0.0, 2.0],(2.0,4.0],(4.0,6.0],(6.0,10.0],(10.0, 15.0],分別計算各區間的中間值為1.0,3.0,5.0, 8.0,12.5,那么評價標準Si,k依次可取值為1.0, 3.0,5.0,8.0,12.5,15.0。

根據各個觀測點的各評價因子實測值,運用上述的隸屬函數計算公式及方法,計算出各實測值在不同水質級別中的隸屬度,從而建立每個觀測點的單因子模糊評價矩陣：

式中：rik為第i個評價因子對于第k級別的隸屬度, i=1,2,…,5;k=1,2,…,6。

3.1.3 確定權重

權重是衡量某一因子對水質影響相對大小的量值,權重系數越大,則該因子對水質的影響程度越大。其確定過程,本質上是客觀的,但在具體應用中,容許有一定的人為技巧,即運用相關數學工具,進行數學解析。本研究中,在確定各評價因子的權重時,首先確定各評價因子的超標比。某指標的實測值相對于水質標準值的超標比越大,說明該指標對污染的貢獻越大,從而權重越大。

對于一般的成本性指標,如NH3-N和TP,超標比計算式為

對于收益性指標,如DO,超標比計算式為

式中：Iji為第j個斷面第i個評價因子的超標比; ρji為第j個斷面第i個評價因子的實測值,mg/L; S0i為第i個評價因子各級別水質標準限值的均值, mg/L,用加權平均算法求得。具體到各水質指標, ρ(DO)為3.75 mg/L,ρ(NH3-N)為1.00 mg/L, ρ(CODMn)為7.5 mg/L,ρ(COD)為20.00 mg/L, ρ(TP)為0.20 mg/L。

計算出超標比后,進行歸一化處理,算出每一個評價因子的權重：

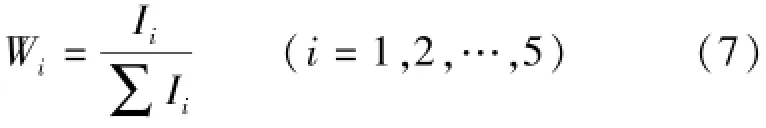
從而可得權重集,W={W1,W2,…,Wj},(j=1,2,…, 6)。

3.1.4 建立評價模型

確定了模糊評價矩陣R和權重集W之后,可建立模糊評價模型：

式中：n為隸屬度的個數。結合最大隸屬度原則,若bj=max(b1,b2,…,bn),則該觀測點處水質級別為第j級,即每一個行向量中,最大隸屬度所處的位置代表了該斷面處水質的級別,然后結合各斷面的評價結果,可以對整個水功能區的水質情況做出綜合評判。

3.2 單因子評價法

采用單因子評價法找到對水質影響最嚴重的一個或幾個影響因子。單因子評價法將各參數濃度代表值與評價標準逐項對比,以單項評價最差項的類別作為水質類別,從而可以確定出超標嚴重的評價因子,其計算公式為

式中：Pi為某評價因子的相對計算值;ρi為某評價因子的實測濃度值;ρsi為某評價因子的最高允許標準值;i=1,2,…5。對于某一類水質標準來說,Pi≤1表明該指標達標,Pi＞1表明該指標超標。

4 計算結果及分析

根據建立起來的評價因子集和評價集,以及不同水質級別的隸屬函數,計算出從上游到下游各斷

面的評價矩陣：

這6個評價矩陣分別代表6個觀測點各評價因子實測值的隸屬度。上述矩陣中,各行依次代表DO、NH3-N、CODMn、COD和TP。根據上述計算權重的公式,計算得各監測斷面各評價因子的權重系數(表1)。

表1 各監測斷面處各評價因子權重系數

根據表1可確定6個權重向量：

W1=[0.103,0.369,0.096,0.172,0.260]

W2=[0.100,0.411,0.083,0.148,0.258]

W3=[0.087,0.417,0.081,0.162,0.252]

W4=[0.089,0.417,0.080,0.139,0.274]

W5=[0.098,0.409,0.080,0.133,0.279]

W6=[0.105,0.404,0.076,0.141,0.275]

再根據模糊評價模型,計算出每個測點的水質級別,即根據式(8)可得：

b1=[0.00,0.00,0.10,0.22,0.05,0.63]

b2=[0.00,0.00,0.05,0.20,0.09,0.67]

b3=[0.00,0.00,0.06,0.14,0.14,0.67]

b4=[0.00,0.00,0.05,0.20,0.06,0.69]

b5=[0.00,0.00,0.04,0.19,0.09,0.69]

b6=[0.00,0.00,0.05,0.16,0.11,0.68]

根據最大隸屬度判定原則,從外秦淮河上游到下游的6個觀測點,最大值分別為0.63、0.67、0.67、0.69、0.69、0.68,而且這6個值均處于第6位的位置上,說明這6個測點的水質級別均為劣Ⅴ類。

對于各指標的貢獻度采用單因子分析,依據上述監測數據,以Ⅴ類水水質標準作為評價準則,計算各個指標的相對計算值,該相對計算值是一個無量綱數。以相對計算值的最大值確定外秦淮河的主要超標因子。計算結果見表2。

表2 各斷面各指標相對計算值

由表2可見,相對計算值最高的是NH3-N,除七橋甕為1.49外,其余5個監測斷面均超過了2.00,最高值在草場門橋斷面出現,可達2.24,表明NH3-N超標嚴重;其次是TP,平均超標1.35倍,最高值出現在草場門橋處,可達1.53倍,表明TP是僅次于NH3-N的影響因子。而DO、CODMn和COD三者的相對計算值均未超過1.0,均滿足Ⅴ類水質標準。單因子評價法的結果表明,外秦淮河中NH3-N和TP是主要的影響因子。即使在七橋甕斷面,水質達到Ⅴ類,NH3-N和TP仍是超標的。

運用其他評價法,包括污染指數法、層次分析法以及模糊物元法等,進行對比驗證,對比結果見表3。由表3可見,改進的模糊數學評價法對各斷面水質的評價結果與其他方法基本一致,與模糊物元法結果相差較大,原因是模糊物元法不能評價劣Ⅴ類水。說明改進的模糊數學評價法用在此處是合理、貼近實際的。

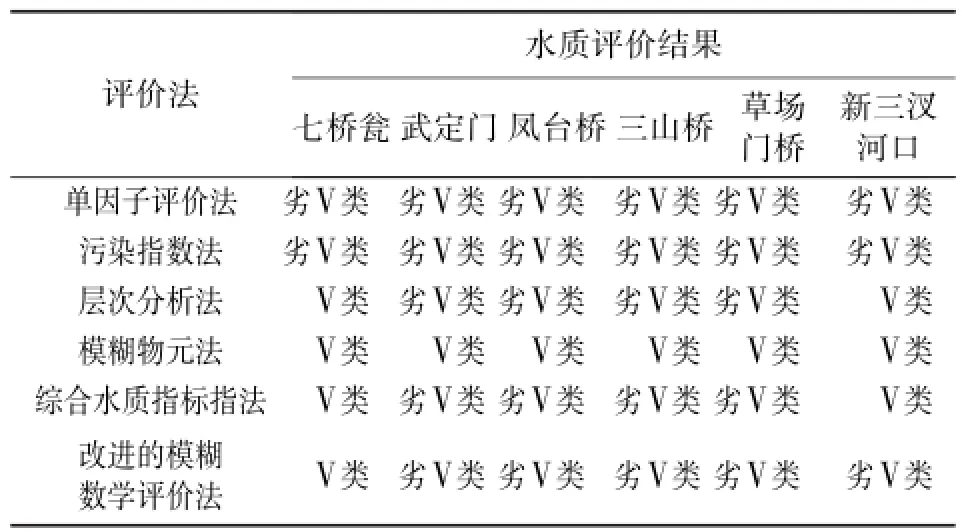
表3 不同水質評價法對外秦淮河水質評價結果對比

同樣的,運用上述方法對各個季度的外秦淮河水質進行評價(圖4)。由圖4可見,外秦淮河水質在各季度有所變化,其中第三季度水質要好于其他季度。

圖4 各季度外秦淮河各斷面綜合水質評價結果

5 結 論

a.改進的模糊數學評價法能夠有效評價出外秦淮河綜合水質狀況,方法合理。

b.從2009年的數據來看,外秦淮河6個觀測斷面的水質均達不到水功能區要求,除七橋甕斷面可達到Ⅴ類水以外,其他5個斷面均處于劣Ⅴ類的水平。

c.造成各斷面水質達不到水功能區要求的原因是,NH3-N和TP全線嚴重超標。NH3-N平均超標2.05倍,TP平均超標1.35倍,其他3個指標均可達到Ⅴ類水水質標準。

[1]劉成,袁琳,余明星,等.河流水質評價方法綜述[J].吉林農業,2012(7)：226-227.(LIU Cheng,YUAN lin,YU Mingxing,et al.Evaluation methods of river water quality [J].Jilin Agriculture,2012(7)：226-227.(in Chinese))

[2]胡海英,包為民,余德華,等.資水流域益陽段水質現狀分析與評價[J].中國農村水利水電,2008(2)：41-44. (HU Haiying,BAO Weimin,YU Dehua,et al.Water quality assessment in the Yiyang Reach of the Zishui Basin[J].China Rural Water and Hydropower,2008(2)：41-44.(in Chinese))

[3]蔣火華,朱建平,梁德華,等.綜合污染指數評價與水質類別判定的關系[J].中國環境監測,1999,15(6)：46-48.(JIANG Huohua,ZHU Jianping,LIANG Dehua,et al. The relationship between comprehensive pollution index assessment and water quality type distinguishing[J]. Environmental Monitoring in China,1999,15(6)：46-48. (in Chinese))

[4]孫靖南,鄒志紅,任廣平.模糊綜合評價在天然水體水質評價中的應用研究[J].環境污染治理技術與設備, 2005,6(2)：45-48.(SUN Jingnan,ZOU Zhiping,REN Guangping.Study on the fuzzy synthetic evaluation for natural water quality[J].Techniques and Equipment for Environmental Pollution Control,2005,6(2)：45-48.(in Chinese))

[5]趙志堅.灰色聚類法在水環境質量評價中的應用[J].四川環境,1997,16(3)：49-51.(ZHAO Zhijian. Application of grey method to water environmental quality assessment[J].Sichuan Environment,1997,16(3)：49-51.(in Chinese))

[6]陳德明,李祚泳.大氣環境質量的物元分析評價法[J].環境科學研究,1994,7(2)：24-28.(CHEN Deming,LI Zuoyong.The assessment of atmospheric environmental quality based on matter element analysis[J].Research of EnvironmentalScience,1994,7(2)：24-28.(in Chinese))

[7]鄧新民,李祚泳.層次分析法用于水環境質量評價[J].成都氣象學院學報,1990(2/3)：70-75.(DENG Xinmin,LI Zuoyong.Application of analytic hierachy process(AHP)in assessment of water environmental quality[J].Journal of Chengdu Institute of Meteorology, 1990(2/3)：70-75.(in Chinese))

[8]秦天玲,侯佑澤,郝彩蓮,等.基于主成分分析的武烈河流域水質評價研究[J].環境保護科學,2011,37(6)：102-105.(QIN Tianling,HOU Youze,HAO Cailian,et al. Study on water quality evaluation of Wulie River Basin based on the method of PCA[J].Environmental Protection Science,2011,37(6)：102-105.(in Chinese))

[9]胡成,蘇丹.綜合水質標識指數法在渾河水質評價中的應用[J].生態環境學報,2011,20(1)：186-192.(HU Cheng,SUDan.Applicationofcomprehensivewater quality identification index in water quality assessment of Hun River[J].Ecology and Environmental Sciences, 2011,20(1)：186-192.(in Chinese))

[10]尹靜章,傅靜,謝營,等.改進的模糊數學評價法在德州市地下水水質評價中的應用[J].治淮,2010(12)：22-25.(YIN Jingzhang,FU Jing,XIE Ying,et al.Application of improved fuzzy evaluation method in Dezhou City groundwater quality evaluation[J].Zhihuai,2010(12)：2-25.(in Chinese))

[11]朱冬楠,李暢游,孫標,等.改進模糊物元模型在湖泊水質評價中的應用[J].人民黃河,2010,32(12)：127-130.(ZHU Dongnan,LI Changyou,SUN Biao,et al. Improved fuzzy matter-element model in lake water quality assessment[J].Yellow River,2010,32(12)：127-130.(in Chinese))

Evaluation of water quality in external Qinhuai River based on improved fuzzy mathematical method

TONG Chaofeng1,Lyu Lirui2,FENG Qian3,SHAO Yuyang2
(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University,Nanjing 210098,China; 2.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China; 3.College of Environment,Hohai University,Nanjing 210098,China)

In view of the uncertainty and fuzziness in the evaluation of river water quality,an improved fuzzy mathematical method was used for comprehensive evaluation of the water quality in the external Qinhuai River,in Nanjing City.The results show that the water quality in most sections of the external Qinhuai River reaches the inferior grade V standard,except in the Qiqiaoweng section.NH3-N and TP are the major indices that affect the water quality.

water quality assessment;improved fuzzy mathematical method;single-factor assessment;NH3-N;TP

X826

A

10046933(2014)04006106

20140310 編輯：徐 娟)

10.3969/j.issn.10046933.2014.04.013

國家自然科學基金重點項目(51339005);國家水體污染控制與治理科技重大專項(2009ZX07317-007-05)

童朝鋒(1973-),男,副教授,博士,主要從事河口海岸動力學水環境模擬研究。E-mail：chaofengtong@hhu.edu.cn