典型管節點的疲勞壽命評估

徐小燕，胡芳，賴芳，王慶豐

(1.江蘇科技大學船舶與海洋工程學院，江蘇鎮江212003;2.滬東中華造船集團有限公司，上海 200129; 3.大連船舶重工集團有限公司，遼寧大連 116000)

典型管節點的疲勞壽命評估

徐小燕1，胡芳2，賴芳3，王慶豐1

(1.江蘇科技大學船舶與海洋工程學院，江蘇鎮江212003;2.滬東中華造船集團有限公司，上海 200129; 3.大連船舶重工集團有限公司，遼寧大連 116000)

針對大型焊接結構在復雜的應力應變場中，結構應力集中的地方往往會萌生裂紋，裂紋擴展損傷積累到一定的程度就會很容易釀成災難性事故的問題，提出了一種運用權函數法求解典型管節點的應力強度因子，采用單一裂紋擴展率曲線模型預估管節點的疲勞壽命。通過與經驗公式的結果對比，發現權函數的方法在計算壽命的時候和經驗公式的結果擬合度很好，而且壽命要比經驗公式偏小，更有利于對壽命的保守估計。該方法簡單方便，具有很強的操作性和可行性。

疲勞斷裂;疲勞曲線;應力強度因子;權函數

0 引言

近年來，隨著我國經濟的高速發展，船舶運輸量也急劇增加，與此同時，水上安全生產形勢也面臨嚴峻的考驗。由于船舶和海洋平臺都是大型的焊接結構，海洋平臺結構龐大，在海洋中受力復雜，所以長期處于波浪力、風力、潮流力等交變載荷的作用下［1］。結構應力集中的地方往往會萌生裂紋，裂紋擴展損傷積累到一定的程度就很容易釀成災難性的事故，以往就存在著許多脆性破壞和疲勞斷裂引起的海洋平臺以及船體事故，影響了經濟效益，造成壞的社會影響。

1 典型節點疲勞壽命的研究現狀及意義

船舶及海洋工程結構物長期處在循環載荷作用下容易產生疲勞裂紋，隨著裂紋的擴展將導致其斷裂或失效，會帶來災難性事故［1］。目前國內外關于疲勞已經有很多的研究方法，主要包括理論計算法、數值仿真法、試驗方法，其中主要的又有S－N曲線方法和斷裂力學法。

確定疲勞裂紋擴展率曲線是基于斷裂力學預測疲勞壽命的關鍵。關于裂紋擴展率模型的研究已經有了不少成果，近年來以Paris公式為基礎，將應力比、裂紋尖端閉合效應、載荷次序效應和應力強度因子門檻值考慮在內，許多學者提出了自己的模型。而Forman公式和Walker公式又提出了應力比影響的修正公式，目前，對載荷遲滯效應的研究主要有Wheeler模型和Willenborg模型。而應力強度因子是在裂紋擴展率模型確定的情況下影響疲勞壽命的預估準確性的主要因素。簡單結構形式的應力強度因子的求解，已經有許多的學者提出了比較成熟的方法，應力強度因子的經驗公式最具代表性的是在Newman-Raju(1979)拉彎應力作用下表面裂紋應力強度因子計算公式，它計算精度高，適用范圍廣。對于復雜結構的應力強度因子的求解，也有一些學者采用不同的方法進行研究，例如運用有限元方法對裂紋體建模，應用交互J積分方法和位移外推插值法直接估算應力強度因子，再運用斷裂力學方法預測它的疲勞壽命。但這些方法需要對裂紋體建模而且對網格的劃分也有很高的要求，耗費了大量的工作時間，可操作性低［2］。

基于國內外對應力強度因子的研究現狀，本文提出了把運用權函數方法求解得到的應力強度因子用于預估典型管節點的疲勞壽命，以T型管節點為對象開展研究。

2 裂紋的擴展和壽命評估的計算

2.1 疲勞裂紋的擴展速率

疲勞裂紋的擴展率是指在疲勞裂紋的緩慢擴展階段內每一次應力循環裂紋所擴展的距離，該速率用Δa/ΔN(mm/周)表示。其中，Δa表示為應力循環ΔN次后裂紋擴展的長度，用微分da/dN表示。

在斷裂力學中，應力強度因子和裂紋長度的關系表達式為:

式中:K為應力強度因子;a為裂紋長度;σ為對應的應力;Y為結構形式有關的參數。若將上述概念用于疲勞，則有:

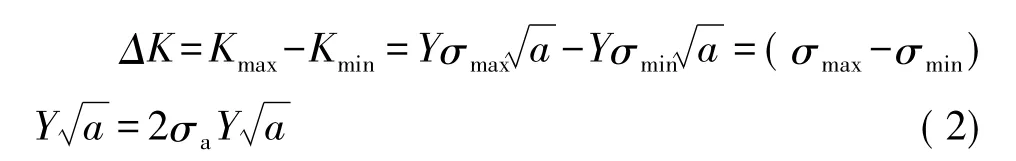
式中:Kmax為最大循環應力所對應的應力強度因子; Kmin為最小循環應力所對應的應力強度因子;ΔK為裂紋前沿應力場強度因子幅。

在一定循環應力條件下，已知一定裂紋擴展長度，就可以求出和它相對應的裂紋擴展速率da/dN，而同時也能求出在一定循環應力條件下的裂紋尖端的應力場強度因子幅ΔK。

而第二階段也是最主要的階段，它是疲勞裂紋擴展壽命的主要組成部分。一般認為，在數學坐標系中da/dN與ΔK呈線性的關系是一條直線(也可用2條直線來描述)，其中Paris公式是其中運用得最為廣泛的一種，表示為:

式中:C和m一般通過實驗測得，是有關實驗條件如環境、頻率、溫度、應力比等的材料參數。

基于斷裂力學理論，本文選取黃小平提出的單一裂紋擴展率曲線模型，建立應力強度因子幅值與疲勞裂紋擴展速率的函數關系表達式，根據材料的斷裂韌性預測T型管節點的疲勞壽命，并將結果與手冊中的K用于預估的疲勞壽命結果相比較。

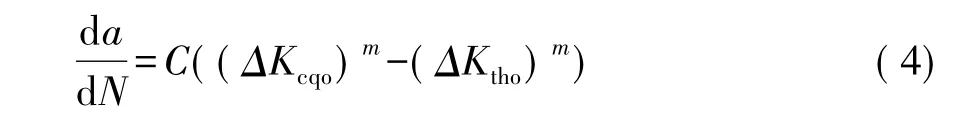
式中:ΔKcqo、ΔKtho分別是當應力比R=0時的等效應力強度因子幅和應力強度因子幅門檻值;C是Paris系數;m是與裂紋擴展有關的指數。

式中:MR是載荷比的修正因子;Mp是載荷次序的修正因子。

MR在wake模型的基礎上修正了載荷比R效應的模型:

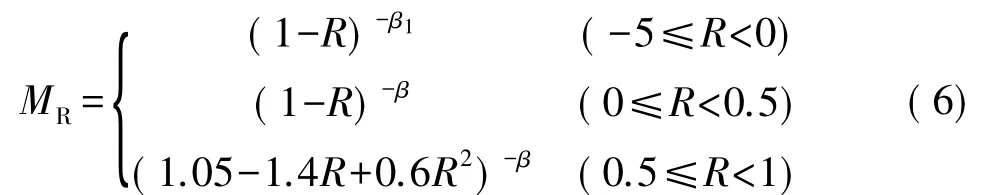
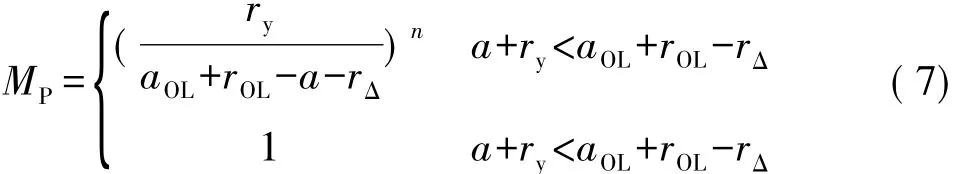
式中:β、β1為形狀系數;aOL是過載時的裂紋半長;ry是裂紋尖端塑性區大小;rOL是過載時裂紋尖端塑性區大小;rΔ是低載-過載引起的裂紋尖端塑性區大小的增量。

船海結構物在服役過程中受到的外力是不斷變化的，因而R也是不斷變化的。通過對MR的計算證明，該模型能更好地描述不同應力比下的裂紋擴展數據［3］。

2.2 裂紋的擴展和壽命評估的計算

本文基于有限元軟件ANSYS和權函數結合的方法對典型管節點結構的裂紋擴展路徑進行數值模擬，具體計算過程如下:

(1)運用有限元軟件對典型節點進行結構建模，并施加邊界條件和載荷，確定結構的應力集中區域。

(2)在典型結構的應力集中區域進行定義裂紋初始長度a0的擴展路徑，通過第一主應力原則，映射第一主應力的分布到路徑上，得到裂紋厚度方向的應力分布，通過函數擬合求出假想裂紋處在無裂紋情況下沿裂紋方向的應力分布函數σx，帶入權函數公式算出。

(3)在裂紋長度a0的基礎上，增加一個大小為a1的裂紋，通過相同的方法計算出K1I的值。

(4)重復(3)的過程，直至其應力強度因子小于斷裂韌性K1C。

(5)擬合得到的數據，代入計算疲勞壽命。

由于應力強度因子K與裂紋長度的關系為:

式中:F為施加的載荷。

3 典型節點的疲勞壽命估算

3.1 材料和有關參數的確定

本文選取Q235鋼作為管節點的材料，16 mm＜板厚≤40 mm，屈服強度為225 MPa，斷裂韌性KIC=;參數的選擇使用BS7910的平均曲線，得到C=9.58×10－9，m=2.74，R=0.9，ΔKth0= 3.2［5］，根據計算得到的應力強度因子。本文用單一曲線模型在不考慮載荷次序效應和殘余應力的情況下得到給定裂紋長度下的擴展率，分別對裂紋擴展率公式進行擬合。

3.2 T型管節點的壽命估算

3.3.1 求解應力強度因子幅值

應用權函數法求解應力強度因子首先要求解假想裂紋表面應力分布函數σx。通過有限元軟件ANSYS建模，得到T型管節點的應力分布，發現最大應力值為154 MPa，并沒有超過材料屈服極限225 MPa。通過提取沿裂紋擴展方向的第一主應力，經數值軟件進行數值擬合，可得到沿裂紋擴展方向的節點表面的第一主應力分布函數σx。

3.3.2 疲勞裂紋擴展壽命計算

已知初始裂紋長度，通過模擬裂紋的擴展路徑擬合第一主應力的分布函數σx，代入權函數計算它的應力強度因子。下面通過Origin軟件擬合得到裂紋擴展深度與應力強度因子的關系見圖1和圖2。

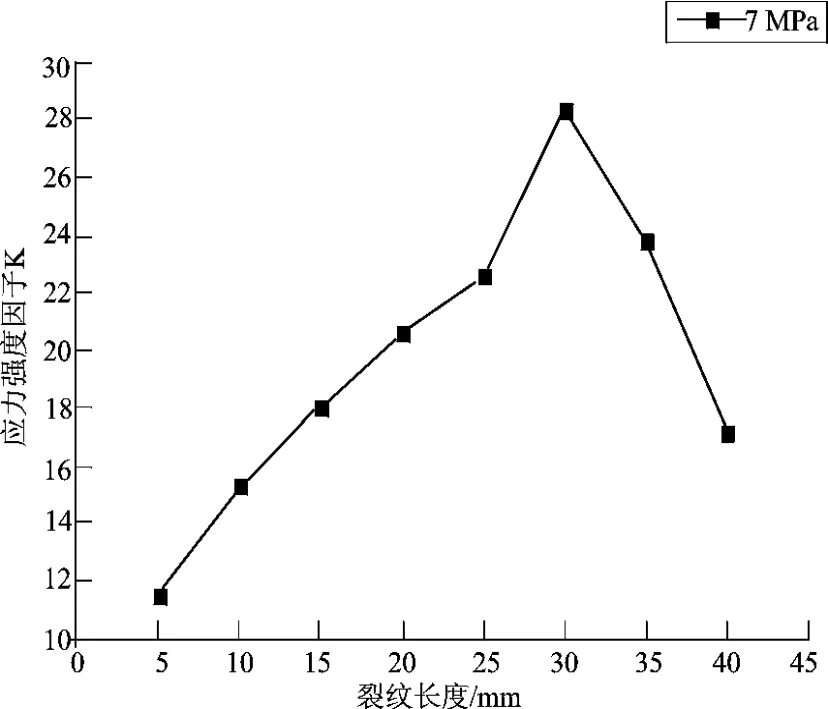
圖1 裂紋長度和應力強度因子曲線(7 MPa)

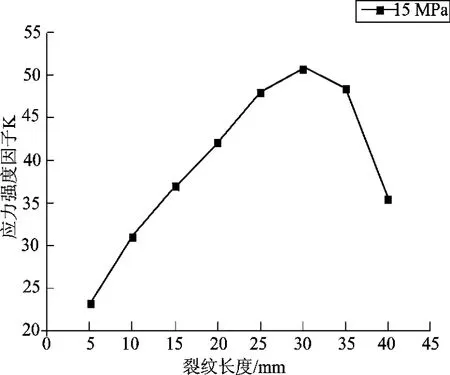
圖2 裂紋長度和應力強度因子曲線(15 MPa)

已知裂紋的初始尺寸，通過計算得到裂紋尖端的應力強度因子K，然后判斷應力強度因子是否滿足脆性斷裂K準則，如果小于斷裂韌性則需要求解下一個裂紋增量所對應的應力強度因子K。通過疊加增量得到新的裂紋尺寸，計算出新的應力強度因子。重復上述的步驟直到裂紋尖端應力強度因子滿足脆性斷裂K準則，則計算結束，分別得到在兩種載荷下的疲勞壽命，如圖3、圖4所示。

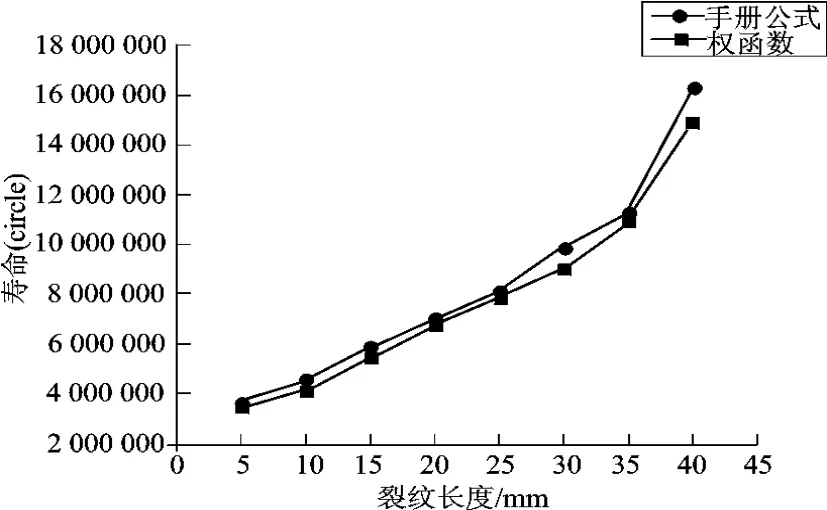
圖3 管節點的壽命評估(15 MPa)

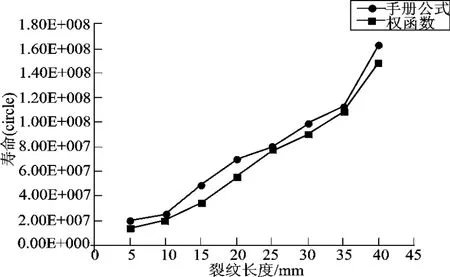
圖4 管節點的壽命評估(7 MPa)

4 結語

本文提出了一種將權函數方法用于計算典型管節點的應力強度因子，以典型的T型管節點為例進行有限元建模，簡化了它在復雜應力場中的應力分布，提取了裂紋最深處的一條第一主應力分布，通過數值擬合應力分布函數代入權函數計算得到它的應力強度因子，將計算出來的應力強度因子幅帶入疲勞擴展壽命計算模型預估它的疲勞壽命。通過比較發現，權函數的方法在計算壽命的時候和經驗公式的結果擬合度很好，而且壽命要比經驗公式偏小，更有利于對壽命的保守估計。

［1］金偉良，龔順風，朱俊民.海洋平臺結構管節點強度可靠性分析［J］.科技通報，2002，9(5):349－354.

［2］趙邦杰.基于權函數法的焊接結構疲勞裂紋擴展壽命計算［D］.大連:大連理工大學，2013.

［3］Huang X P，Moan T.Improved modeling of the effect of R-ratio on crack growth rate［J］.Int.J Fatigue，2007，29:591－602.

［4］趙章焰，呂運冰，孫國正.J積分法測量低碳鋼Q235的斷裂韌性KIC［J］.武漢理工大學學報，2002，24(4):111－112.

［5］趙邦杰.基于權函數法的焊接結勞裂紋擴展壽命計算［D］.大連:大連理工大學，2013.

U661.4

A

2013-12-28

徐小燕(1988－)，女，碩士研究生，研究方向為船舶結構設計及強度;胡芳(1974－)，女，高級工程師，研究方向為船體設計;賴芳(1974－)，女，工程師，研究方向為船舶制造及管理;王慶豐(1976－)，男，副教授，碩士生導師，主要研究方向為船舶結構設計及強度、船舶制造工藝力學。