1維光子晶體中TM波的傳輸公式及其辨析

劉啟能

（重慶工商大學計算機科學與信息工程學院，重慶400067）

1維光子晶體中TM波的傳輸公式及其辨析

劉啟能

（重慶工商大學計算機科學與信息工程學院，重慶400067）

為了得到1維光子晶體中TM波的傳輸公式，采用傳輸矩陣的方法和電磁波的邊界條件，推導出TM波在介質層中的特征矩陣及其反射系數和透射系數公式。結果表明，用TE波反射系數和透射系數公式做代換的方法不能得到正確的TM波的反射系數和透射系數公式；對推導出TM波的反射系數和透射系數公式進行了分析，由TM波的反射系數和透射系數公式得出的光強透射率和反射率滿足能量守恒；并且推出的TM波反射系數公式不僅能夠反映反射波與入射波的數量關系，且能夠反映反射波與入射波的位相關系。這些結果對研究1維光子晶體中TM波的傳輸性質是有幫助的。

材料；光子晶體；TM波；反射系數；透射系數

引 言

光子晶體的概念自JOHN和YABLONOVITCH于1987年提出來后，由于利用光子晶體的帶隙可以十分方便地控制光波的傳播，光子晶體的研究很快成為光學的前沿領域內一個活躍的課題［1-6］。在光子晶體的研究中由于1維光子晶體的結構最簡單、研究最方便，但它卻具有其它高維光子晶體的基本屬性。因此對1維光子晶體的研究成為光子晶體研究領域內的重要內容［7-12］。

1維光子晶體的研究方法中特征矩陣法是最基本、最重要的方法，但在現有的文獻［13-14］中僅對電矢量垂直于入射面的TE波通過介質層的特征矩陣以及反射系數和透射系數公式進行了推導，而對電矢量平行于入射面的TM波通過介質層的特征矩陣以及反射系數和透射系數公式沒有做推導，僅是將TE波的特征矩陣以及反射系數和透射系數公式做代換得到TM波的特征矩陣以及反射系數和透射系數公式。由于TM波的特征矩陣以及反射系數和透射系數公式是研究1維光子晶體的基本公式，它們的正確與否直接決定著1維光子晶體的研究結果，因此必須弄清這一問題。作者將推導出TM波的特征矩陣以及反射系數和透射系數公式，結果發現，對于TM波的特征矩陣公式上述代換是正確的，但是對于TM波的反射系數和透射系數公式上述代換是不正確的。

1 公式推導

［13］中關于TE波通過介質層的特征矩陣以及反射系數和透射系數公式是正確的，這里直接列出其特征矩陣M：

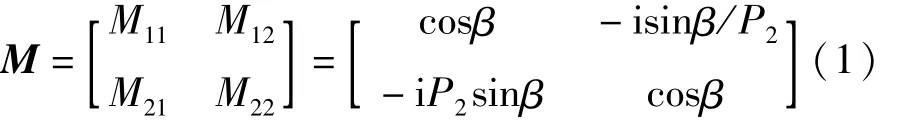
TE波的反射系數rTE和透射系數tTE為：

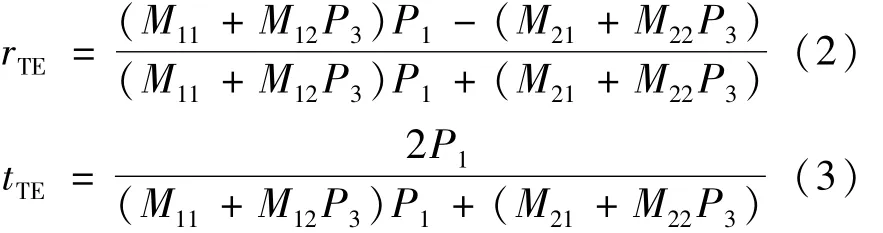
式中表示入射空間，下標3表示出射空間。

下面推導TM波的特征矩陣以及反射系數和透射系數公式。設TM波從介質1入射到厚度為d2的介質層2，通過介質層2后透射，如圖1所示。。下標1

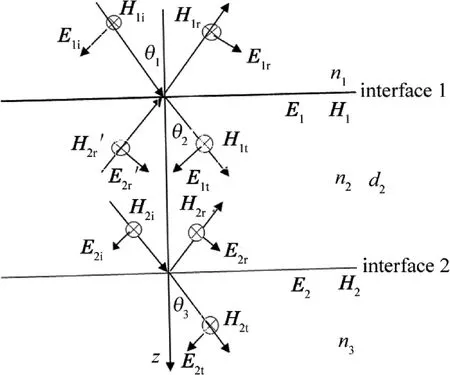
Fig.1 TM wave propagation in dielectric layer

圖1 中，E1和H1表示界面1兩側的電矢量和磁矢量的切向分量，E2和H2表示界面2兩側的電矢量和磁矢量的切向分量。下面計算中討論的分別是各分矢量對應的標量。對于界面1，切向分量E1和H1連續有：

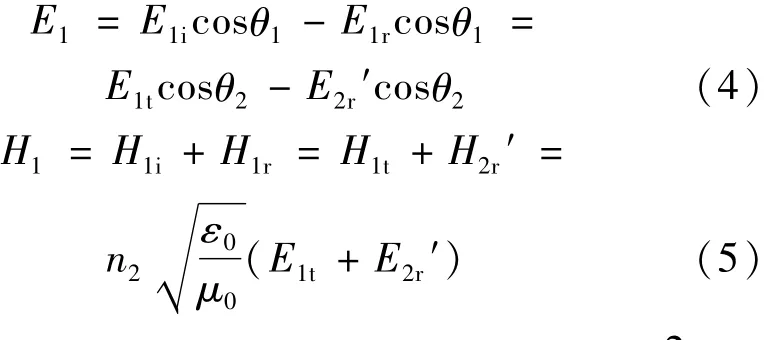
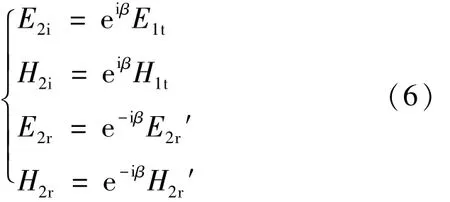
對界面2，切向分量E2和H2連續有：

由（7）式和（8）式得：

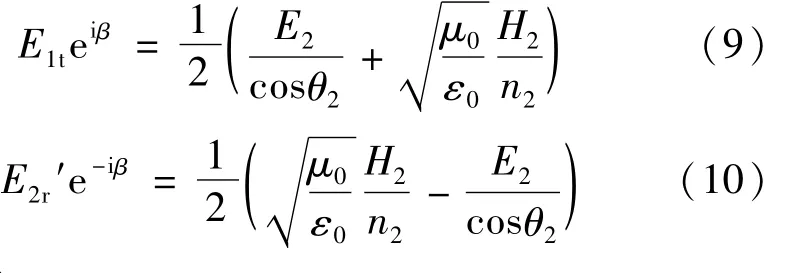
將（9）式和（10）式代入（4）式和（5）式得：

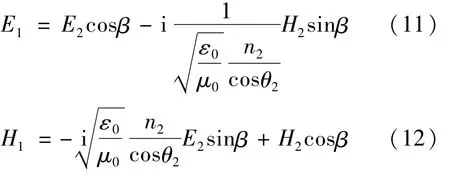
將（11）式和（12）式表示為矩陣關系：

其特征矩陣為：

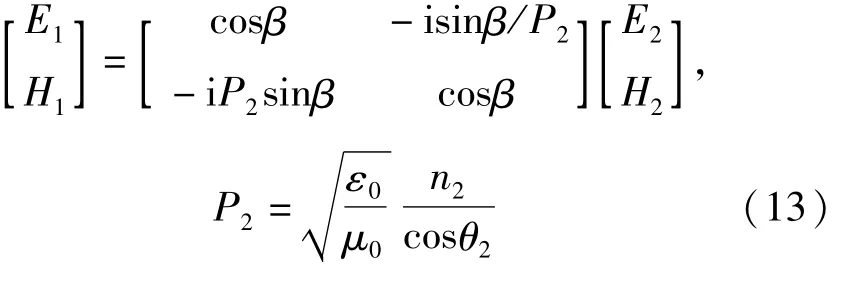
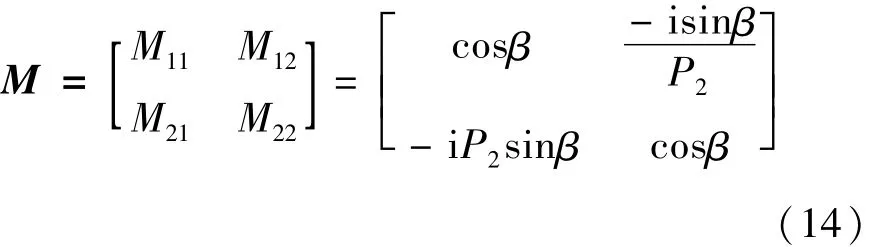
比較（14）式與（1）式可以看出，TM波的特征矩陣與TE波的特征矩陣形式相同，只不過是將（1）式的因此，對于TM波的特征矩陣可以通過對TE波的特征矩陣做替換的方法得到。

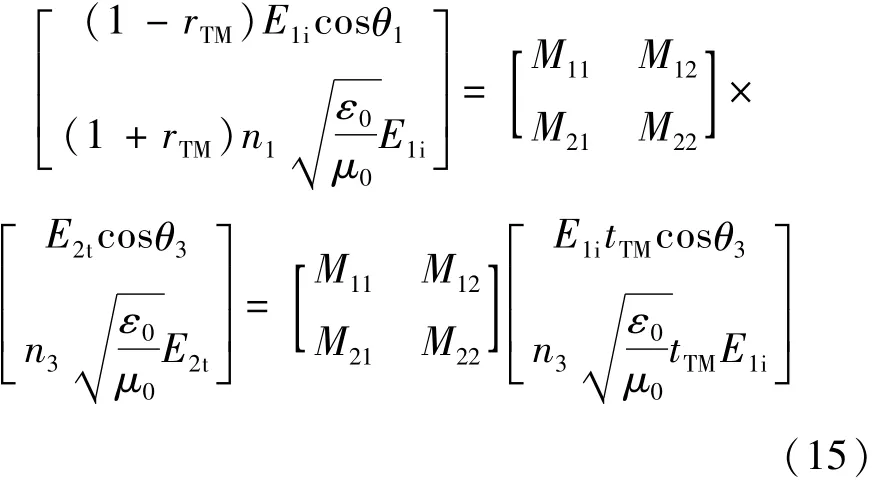
展開（15）式得：

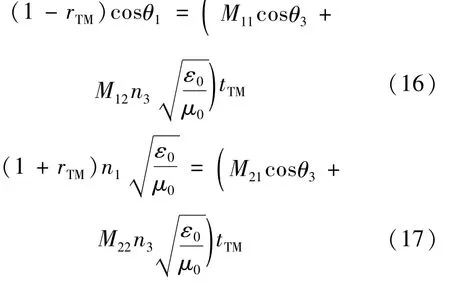
由（16）式和（17）式解出反射系數和透射系數分別為：

2 公式分析

下面進一步利用TM波的反射系數和透射系數公式來說明入射波、反射波和透射波的能量關系以及反射波與入射波的位相關系。

2.1 能量守恒

由圖1可知，TM波沿z軸的入射能流密度Siz、反射能流密度Srz、透射能流密度Stz滿足：

TM波光強的反射率R和透射率T分別為：

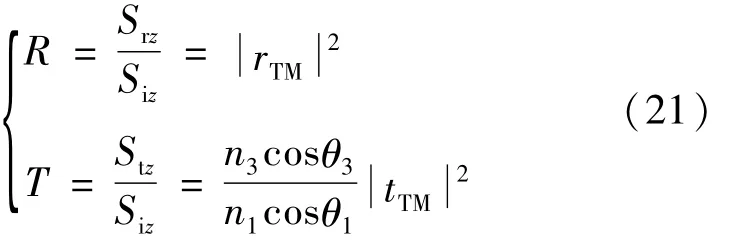
取n1＝1（空氣），n2＝1.8（氧化鋁），n3＝2.38（硫化鋅），d2＝200nm，λ＝600nm，利用（21）式計算出反射率R和透射率T隨入射角的響應曲線，如圖2所示。圖2中的R為反射率曲線、T為透射率曲線、實線為R＋T隨入射角的響應曲線。由圖2看出：入射角在0～π／2范圍內變化時恒有R＋T＝1，這表明由TM波的反射系數和透射系數公式推出的反射率R和透射率T滿足能量守恒。從而驗證了本文中推導的TM波的反射系數和透射系數公式的正確性。

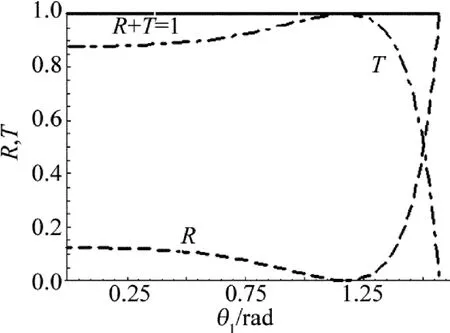
Fig.2 Response curves of reflectance and transmittance versus incident angle（in new formula）

如果按照參考文獻［13］中將TE波的反射系數和透射系數公式中的P換為的方法得到的TM波光強的反射率R′和透射率T′分別為：

取n1＝1（空氣）、n2＝1.8（氧化鋁）、n3＝2.38（硫化鋅）、d2＝200nm、λ＝600nm。利用（22）式計算出反射率R′和透射率T′隨入射角的響應曲線，如圖3所示。圖3中的R′為反射率曲線、T′為透射率曲線、實線為R′＋T′隨入射角的響應曲線。由圖3看出：入射角在0～π／2范圍內變化時有R′＋T′不恒等于1，即不滿足能量守恒定律。因此用代換的方法得出TM波的反射系數和透射系數公式是錯誤的。

Fig.3 Response curves of reflectance and transmittance versus incident angle（in old formula）

2.2 位相關系

考察TM波和TE波垂直入射的情況下其反射波與入射波的位相關系，如圖4所示。由圖4看出：當TM波垂直入射時，其反射波的電矢量分量E1r與入射波的電矢量分量E1i方向相反，即是反相的。而TE波垂直入射時，其反射波的電矢量分量E1r與入射波的電矢量分量E1i方向相同，即是同相的。

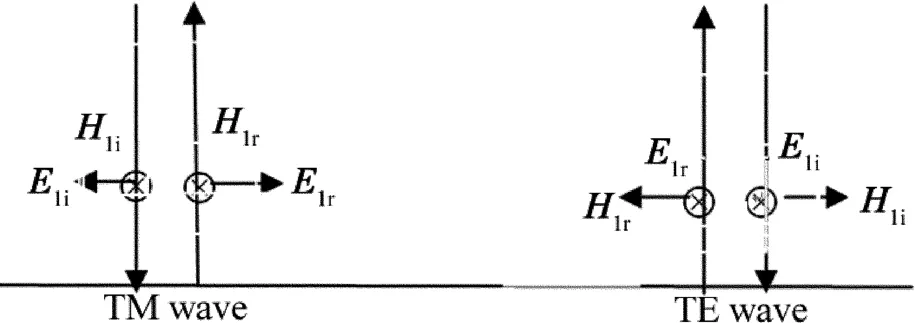
Fig.4 The reflection wave and incident wave phase relationship of TM wave and the TE wave veltical incidence

（23）式表明，垂直入射時TM波的反射波與入射波的位相關系和TE波的情況相同。而從圖4中知道，垂直入射時TM波的反射波與入射波的位相關系和TE波的情況相反。因此（23）式是不正確的，即把TE波的反射系數公式中的P替換為后作為TM波的反射系數是不正確的。

再用（18）式研究這一問題，由（18）式會直接得出在垂直入射情況下TM波的反射系數為：

（24）式正是圖4中反映出的結果，即垂直入射時TM波的反射波與入射波的位相關系和TE波的情況相反。因此，本文中推出的TM波的反射系數公式不僅能夠反映反射波與入射波的數量關系，而且還能反映反射波與入射波的位相關系。

3 結 論

前面利用TM波在界面切向分量連續的條件，推導出TM波在介質層中的特征矩陣及其反射系數和透射系數公式。并對推導出TM波的反射系數和透射系數公式進行了分析，結果表明，推出的TM波的反射系數和透射系數公式滿足能量守恒。TM波的反射系數公式不僅能夠反映反射波與入射波的數量關系，而且還能反映反射波與入射波的位相關系。而目前文獻中介紹的將TE波反射系數和透射系數TM波的反射系數和透射系數公式不滿足能量守恒，因此它是錯誤的。

由于TM波的反射系數和透射系數公式是1維光子晶體研究中的重要公式，因此本文中推出的TM波的反射系數和透射系數公式對研究TM波在1維光子晶體中的傳輸特性有著重要的意義。

參考文獻

［1］ WANG R，ZHANG C X，NIE Y H.Band structure and propagation properties of one-dimension anisotropy photonic crystalsl［J］.Acta Photonica Sinica，2007，36（1）：89-92（in Chinese）.

［2］ LIR，REN K，RNE X B.Angular and wavelength selectivity of band gapsof holographic photonic crystals for differentpolarizations［J］.Acta Physica Sinica，2004，53（8）：2520-2523（in Chinese）.

［3］ LIU Q N.A new simple and convenientmethod for study of properties forbidden band of one-dimensional photonic crystal［J］.Acta Photonica Sinica，2007，36（6）：1031-1034（in Chinese）.

［4］ LIUQN.Effectof impurity absorption on one-dimensional photonic crystal defect mode［J］.Chinese Journal of Lasers，2007，34（6）：777-780（in Chinese）.

［5］ LIU Q N.Themode and defectmode of electromagnetic wave in rectangular doped photonic crystal［J］.Acta Physica Sinica，2010，59（4）：2551-2555（in Chinese）.

［6］ XU JP，WANG LG，YANG Y P.Realization of an angular filter using one-dimensional photonic crystal containing negative refractivemetamaterials［J］.Acta Physica Sinica，2006，55（6）：2765-2768（in Chinese）.

［7］ LIUQN.The defectmode and the quantum effect of lightwave in cylindrical anisotropic photonic crystal［J］.Acta Physica Sinica，2011，60（1）：0142171（in Chinese）.

［8］ LIU Q N，HU Ch H.Polarization and total reflection tunnel effect of flat-panel photonic crystal［J］.Laser Technology，2012，36（1）：114-118（in Chinese）.

［9］ LIU Q N.Quantum effect and defectmode of anisotropic rectangle doping photonic crystal［J］.Laser Technology，2011，35（4）：499-503（in Chinese）.

［10］ LIU Q N.Defectmodes of Ag-doped photonic crystal［J］.Semiconductor Optoelectronics，2009，30（5）：703-707（in Chinese）.

［11］ LIU Q N.Total reflection through effect of light in 1-D photonic crystal［J］.Acta Photonica Sinica，2011，40（2）：232-235（in Chinese）.

［12］ LIU Q N.Theoretic study of total reflection through effect polarization filter of photonic crystal［J］.High Power Laser and Particle Beams，2011，23（4）：1091-1094（in Chinese）.

［13］ JIJR.Higher optical tutorial［M］.Beijing：Science Press，2007：133-134（in Chinese）.

［14］ FOWLESG R.Introduction to modern optics［M］.Shanghai：Shanghai Science and Technology Dubusling House，1984：96-104（in Chinese）.

Transm ission formula and analysis of TM wave in 1-D photonic crystal

LIU Qineng
（College of Computer Science and Information Engineering，Chongqing Technology and Business University，Chongqing 400067，China）

In order to obtain transmission formula of TM wave in 1-D photonic crystal，the characteristicmatrix and the reflection and transmission coefficients of TM wave in dielectric layerwere deduced based on the transfermatrixmethod and the boundary conditions of electromagnetic wave.The results show that the reflection and transmission coefficients of TM wave converted from the reflection and transmission coefficients of TE wave were not correct.And then，the deduced reflection and transmission coefficients of TM wave were analyzed.The transmittance and reflectance of TM wave intensity satisfies the law of energy conservation.Reflection coefficient formula of TM wave can not only reflect the relationship between the number of reflection wave and incidentwave，butalso reflect the phase relationship between the reflection wave and incidentwave TM wave reflection coefficient formula can reflect the reflection wave and incidentwave number and the phase relation.These results are helpful for study of transmission properties of TM wave in 1-D photonic crystal.

materials；photonic crystal；TM wave；reflection coefficient；transmission coefficient

O436

A

10.7510／jgjs.issn.1001-3806.2014.03.009

1001-3806（2014）03-0325-05

重慶市教委科技研究基金資助基金項目（KJ130713）

劉啟能（1957-），男，教授，從事光學與聲學研究。

E-mail：liuqineng57＠163.com

2013-07-03；

2013-09-03