基于灰色系統理論的兵團棉花產量預測研究
賈佳 康順光
新疆是我國棉花重要種植基地,而生產建設兵團棉花種植面積約占新疆的三分之一,產量約占全國的六分之一.棉花產業是兵團國民經濟的重要組成部分,同時在兵團經濟發展中有舉足輕重的作用.進一步發揮兵團棉花資源的特殊優勢,大力加強兵團棉花基地建設,對于更好地發揮兵團的“三大作用”,正確處理好“三大關系”,穩疆興疆,富民固邊,不斷增強兵團屯墾戍邊經濟實力都有著十分重要的戰略意義。
灰色預測法是一種對含有不確定因素的系統進行預測的方法.灰色預測是對既含有已知信息又含有不確定信息的系統進行預測,就是對在一定范圍內變化的與時間有關的灰色過程進行預測.灰色預測法常見類型是灰色時間序列預測,即用觀察到的反映預測對象特征的時間序列來構造灰色預測模型,預測未來某一時刻的特征量,或達到某一特征量的時間[1]。由于棉花產業的發展具有明顯的動態特征和不確定性,這符合灰色系統的一般特點,應用灰色系統理論對棉花產量進行動態預測是切實可行的。因此,本文將采用灰色系統理論,對兵團棉花產量建立GM(1,1)模型,并運用該模型對近五年的兵團棉花產量作出灰色預測,對于棉花市場宏觀調控、棉花出口及加工等決策具有一定的參考價值。
1 灰色GM(1,1)模型預測方法
第一步:灰色生成[2]。記原始序列為 X(0)={X(0)(1),X(0)(2),…,X(0)(n)},原始數據累加以便弱化隨機序列的波動性和隨機性,得到一次累加序列1-AGO序列:X(1)={X(1)(1),X(1)(2),…,X(1)(n)},其中
第二步:建立GM(1,1)模型。GM(1,1)的灰微分方程為

記,其中為發展系數,則灰微分方程的最小二乘估計參數列滿足下式

其中
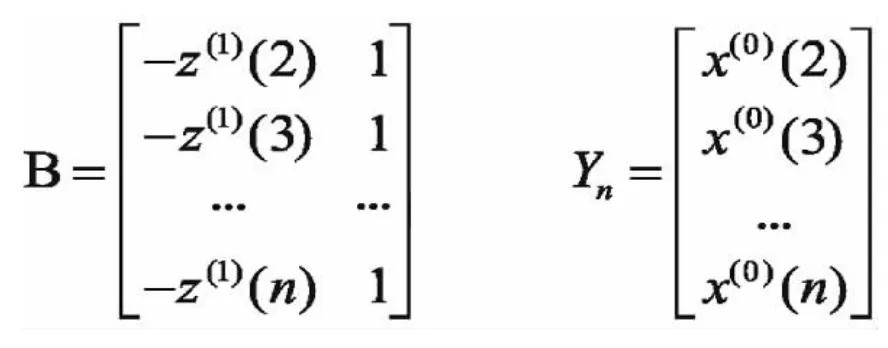
綜上所述,則有

(2)GM(1,1)灰色微分方程的時間響應序列為
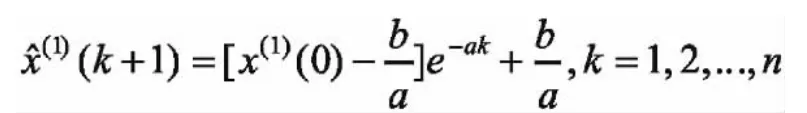
(3)取,則
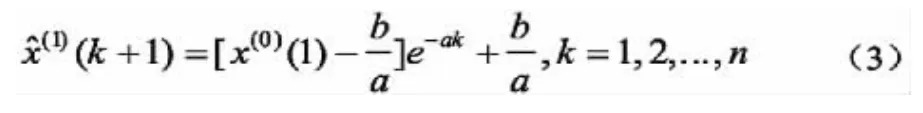
(4)還原值,得到預測方程
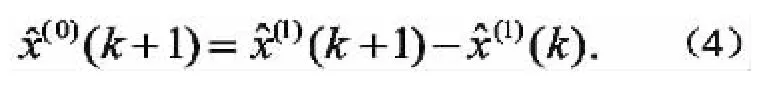
第三步:檢驗 GM(1,1)模型。GM(1,1)模型的檢驗分為三個部分,即是殘差檢驗、關聯度檢驗和后驗差檢驗。
①殘差檢驗:殘差檢驗,相對誤差
②關聯度檢驗:

其中,λ∈[0,1]為分辨系數,一般情況下 λ =0.5吳濤等通過對關聯度系數存在不合理下限分析,認為關聯度不適合于 GM(1,1)模型的檢驗[3],因此,可以不采用關聯度對 GM(1,1)模型進行檢驗。
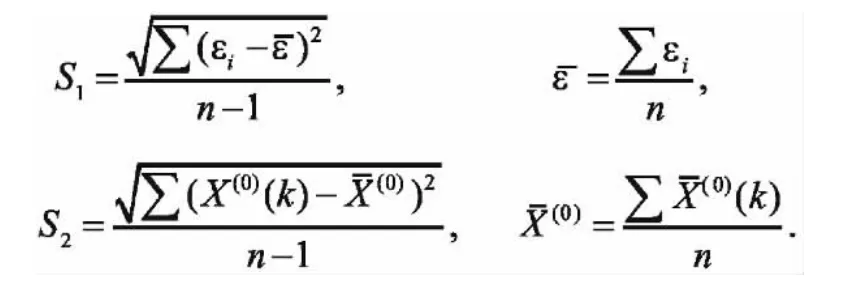
通過下面后驗差檢驗判別參照表(表1),可以判斷模型的精度。
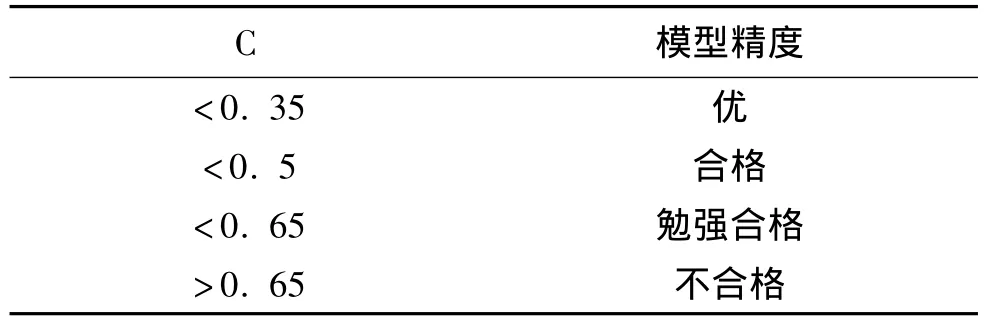
表1 后驗差檢驗判別參照表
第四步:判斷GM(1,1)模型的適用條件,根據灰色預測模型的相關結論,當預測模型的發展系數|α|<2滿足時,模型才有意義。當-α分別符合以下條件時,模型適用于不同情況的預測[4]。
① -α≤0.3時,GM(1,1)可用于中長期預測。
②0.3 < - α≤0.5時,GM(1,1)可用于短期預測,中長期預測慎用。
③0.8<-α≤1時,應采用殘差修正GM(1,1)模型。
④1<-α≤2時,不宜采用GM(1,1)模型。
2 案例分析
根據 2012年新疆建設兵團統計年鑒[5],由2001~2012年新疆生產建設兵團的棉花產量,首先根據建立的GM(1,1)模型對兵團2001~2012年的棉花產量進行預測,并與該12年的實際棉花產量進行對比得到誤差很小。接著應用該模型預測2013~2015年的新疆生產建設兵團棉花產量,并對預測結果做檢驗。
2.1 兵團棉花產量預測模型的參數估計
根據原始時間2001~2012年的兵團棉花產量序列 X(0)(K),對 X(0)(K)生成 1-AGO序列X(1)(K),同時可得 Yn,見表2。

表2 原始序列x(0)、生成1-AGO序列列x(1)(K)以及Yn
其中,X(0)=AGOX(1),即,
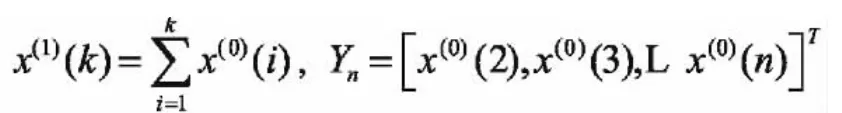
由上式可知,因此,可以選擇GM(1,1)預測模型對新疆建設兵團的棉花產量做中長期預測。
2.2 模型檢驗與兵團棉花產量的預測
2.1 模型檢驗
利用MATLAB編程對新疆建設兵團近12年的棉花產量預測值與實際值進行比較,運行結果見表3,從比對結果可以看出模型的預測值和實際值偏差不大;并且對其進行后驗差檢驗,經過計算,得到后檢驗參數C=0.25<0.35,精度為優,因此該模型可以對兵團棉花產量進行預測。

表3 2001~2012年兵團棉花產量的GM(1,1)灰色系統預測值與實際值比較
2.2 兵團棉花產量的預測
對2013~2015年的兵團棉花產量進行預測,畫出預測值和實際值的變化曲線如圖1所示。
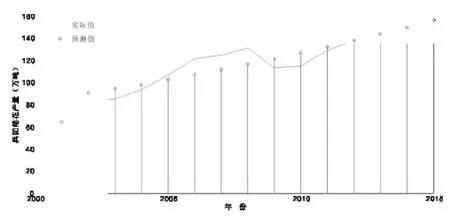
圖1 2000~2015年兵團棉花產量的GM(1,1)灰色預測值
由運行結果可知2013~2015年兵團棉花的預測年產量分別為144.00萬噸、150.17萬噸和156.60萬噸,并且從圖1可知從2010年起棉花產量呈遞增趨勢,基本符合兵團經濟發展趨勢。
3 結論
通過GM(1,1)模型檢驗發現該模型檢驗值和預測值相差不大,模型精度很高,用此模型檢驗兵團棉花產量是可行的。但是由于棉花產量會受到氣候、地質災害等一些因素的影響,預要使預測結果更加精確,需要對此模型進行完善。
[1] 李智鵬,李江宏.基于灰色系統理論的新疆水果產量預測[J].中國科技投資,2013(09):92-93.
[2] 汪曉銀,周保平.數學建模與數學實驗[M].第二版,北京:科學出版社,2012:267-274.
[3] 吳濤,李必強,錢正芳.GM(1,1)模型的關聯度檢驗分析[J].武漢理工大學學報,2002(24):85-87.
[4] 孔令云,沈鵑.灰色預測模型GM(1,1)預測精度淺析[J].公路交通科技,2008(25):346-349.
[5] 新疆生產建設兵團統計局.國家統計局兵團調查總隊[M].北京:中國統計出版社,2012:24-66.

