基于NX8.5的打緯搖軸載荷及模態分析

楊劍宇

打緯機構是織機的五大機構之一，它將緯紗打入織口，使經緯紗交織，形成符合設計要求的織物。目前，織機的打緯機構主要分為共軛凸輪式和連桿式兩類。由于共軛凸輪式打緯具有動程小、運行平穩等優點，故高速的劍桿織機常采用共軛凸輪式打緯機構。而打緯搖軸是共軛凸輪式打緯機構的重要零件之一，其在打緯過程中，需要承受來自凸輪和滾子的較大載荷。另外，打緯搖軸伴隨著旋轉，自身和其他外界因素激勵而發生共振，易造成打緯機構的機件損壞。同時，隨著現代織機向高速、高效、高品質和高適應性方向的發展，對織機的打緯機構主要部件提出了更高的要求。因此，需要更正確地計算搖軸在載荷下的應力、應變和固有頻率等參數，以提高零件在工作時的安全性。

UGNX是一款集CAD/CAM/CAE于一身的企業級的軟件。其中，它的有限元分析，也就是高級仿真模塊，在長時間的發展中吸納了很多世界優秀的有限元軟件，如 MSC.Nastran、I-deals、Adina和 LSDYNA等眾多的功能和優點，特別是它的結構分析功能具有計算精度高、運行速度快、操作界面友好的優勢，得到了國防、航空航天、車輛、船舶、機械和電子等眾多行業的接受和認可，其分析結果已成為航天等級工業CAE標準，獲得美國聯邦航空管理局（FAA）認可。它的高級仿真模塊包含NX前、后處理和NXNastran求解3個基本的組成部分，并具備了在眾多領域中解決工程問題的解算類型。本文通過NX8.5軟件完成了打緯搖軸的建模，并對其進行模態及在載荷下應力應變的分析，為合理設計打緯搖軸提供理論依據。

1 打緯搖軸模型的建立

織機的打緯機構目前主要分為共軛凸輪式和連桿式2類，其中具有小動程、運行平穩等優點的共軛凸輪式常用于劍桿織機。共軛凸輪式打緯機構示意圖如圖1所示。

打緯搖軸是共軛凸輪式打緯機構的重要零件。本文利用NX軟件對打緯搖軸進行了模型的建立。建立的模型如圖2所示。

2 打緯搖軸載荷條件下的分析

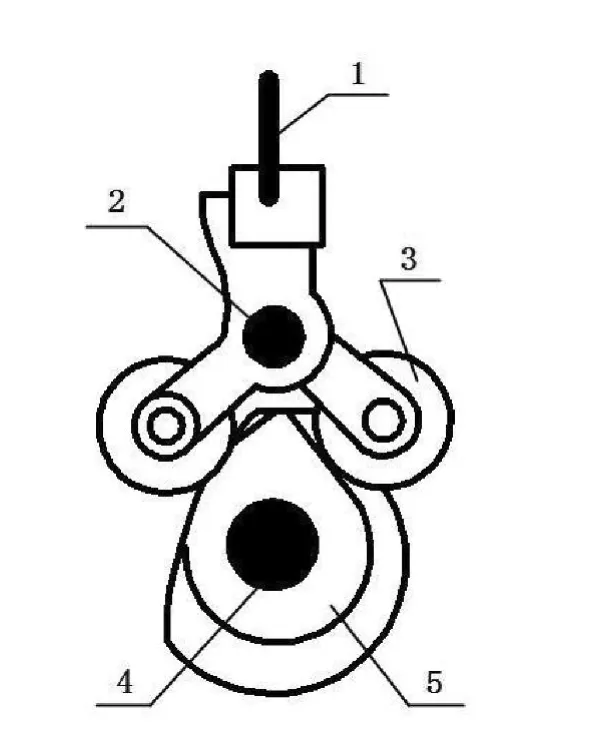
圖1 打緯機構示意圖

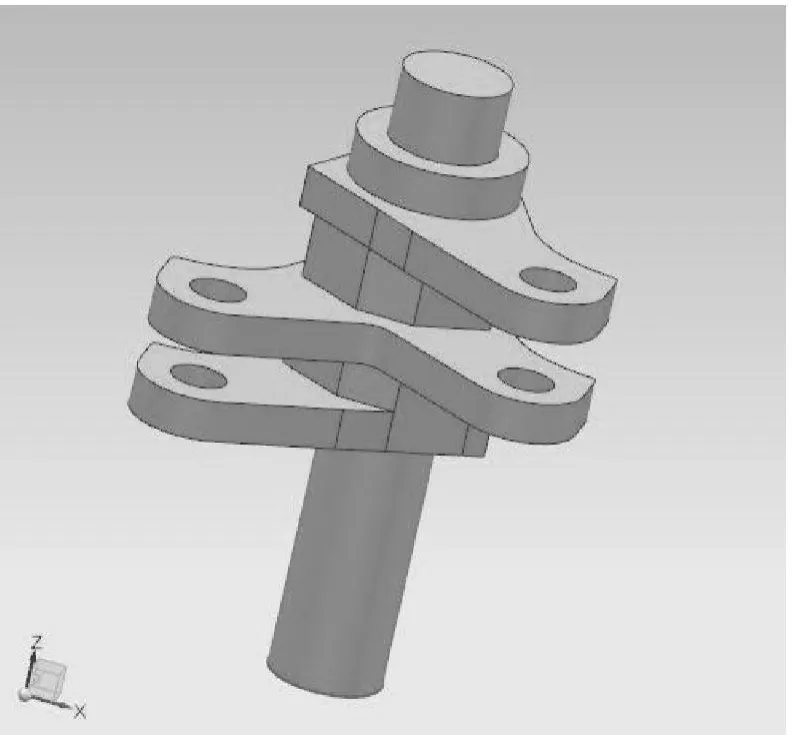
圖2 NX軟件建立的打緯搖軸模型

圖3 打緯搖軸的單元網格劃分

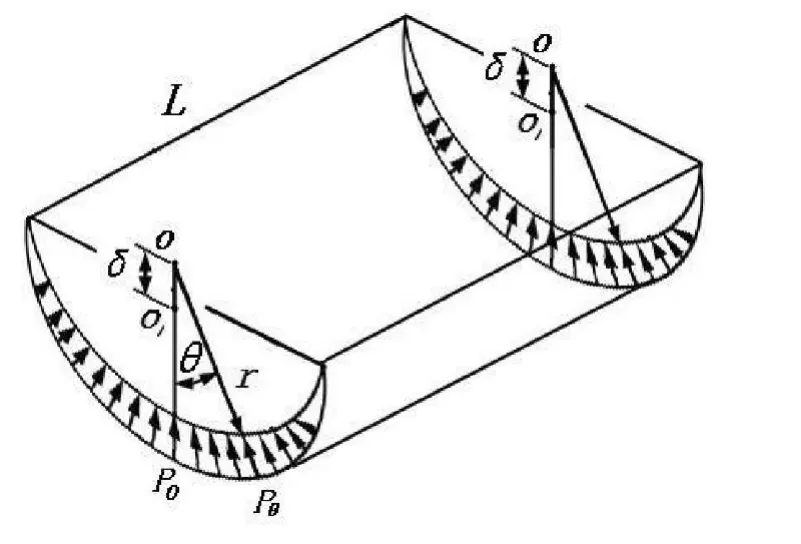
圖4 載荷分布示意圖

2.1 單元劃分

單元網格的劃分是有限元分析前處理工作之一，也是有限元分析計算的基礎。網格質量的優劣是決定計算精度的重要環節，特別是對于大型和復雜模型來說，網格劃分相當耗時，所以一味的減少單元大小對提供計算精度沒有益處。根據模型和單元類型的特點，本文中打緯搖軸采用CTETRA（10）四面體10節點進行劃分，單元大小采用10mm。單元劃分后的模型如圖3所示。

2.2 定義材料屬性

不同的分析和解算類型需要定義不同的材料參數，其中質量密度、楊氏模量和泊松比是彈性范圍內靜力學分析最基本的3個參數。本文中打緯搖軸的材料采用40CrNiMoA。其中質量密度 約為7830kg/m3，楊氏模量約為209GPa，泊松比約為0.3，抗拉強度b≥980 MPa，屈服強度s≥835 MPa。

2.3 載荷的施加及模型的約束

在施加外部載荷的作用下，會使打緯搖軸產生應力和應變，而約束條件不同也會對最終的計算結果起到很大的作用影響。

打緯搖軸的滾輪軸孔上的徑向壓力不是均勻的，它的受力方式如圖4所示。圖中為軸孔的軸向長度。

本文中假設打緯搖軸的滾輪軸孔在受到載荷后仍保持或近似保持圓形，在最大受力P0處的徑向變形為 ，則圓心角為 處的軸孔徑向形變量為 ()=cos滾輪軸孔上受到的壓力方向均沿徑向方向垂直于軸孔表面。設滾輪軸孔的材料應變系數為 k，則最大壓力P0處為：

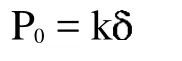
進而得出在任意的圓心角 處軸孔表面受到的壓力為

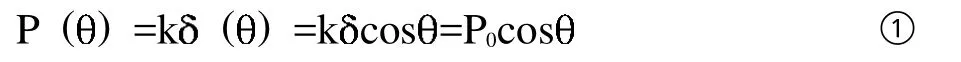
同時，打緯搖軸的滾輪軸孔受到的力是沿孔徑向120°范圍內，按照余弦方式施加到軸孔上的，那么將每個點上的力按x軸和y軸方向分解后分別為：

最后，其應用場景滿足5000萬像素以上的全畫幅數碼相機，同時可以滿足當前8K視頻技術的高分辨率要求，是一支著眼于未來的高品質鏡頭。

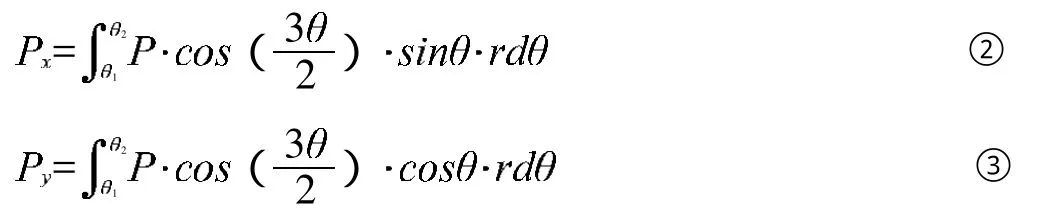
式中，r為孔的半徑， 為圓心角，P為120°弧段中點處的表面力的集度。

根據式①、②和③，得出軸孔在x軸和y軸的載荷 、 ：

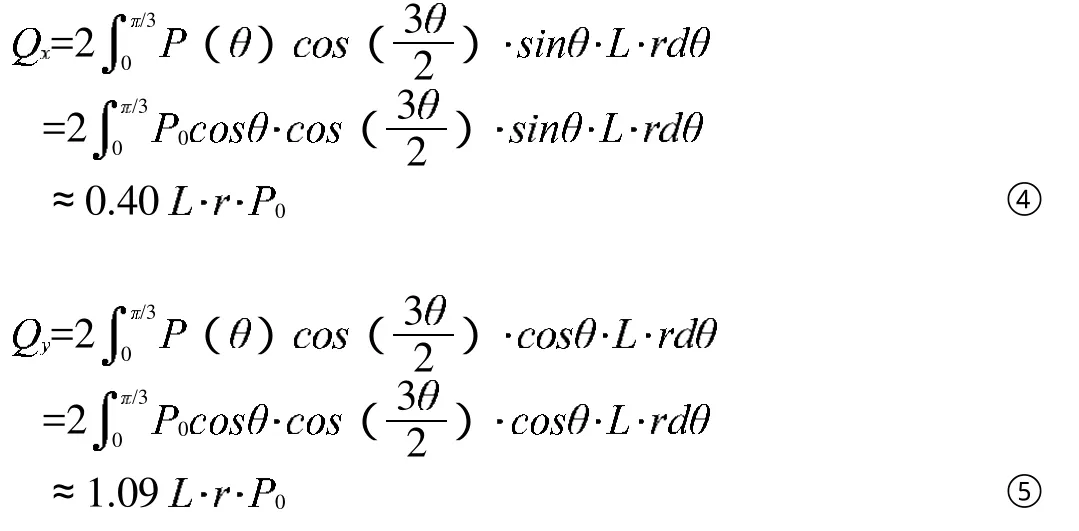
按照式④和⑤可以算出打緯搖軸的滾輪軸孔上x軸和y軸的載荷，并在NX高級仿真模塊中將所計算的載荷施加在軸孔表面上。

配合ADAMAS軟件計算得出：

打緯載荷在主動輪滾輪軸孔處為 =4743.7 =12807.9

從動輪輪滾輪軸孔處為 =5467.9 =-14763.5

另外，在施加載荷的同時，也需要對模型進行約束。打緯搖軸受力的最大值是在打緯時的瞬間靜止狀態,因此將兩端圓柱面施加固定約束，即DOF1、DOF2、 DOF3、 DOF4、DOF5和DOF6均設置為固定，用以模擬打緯搖軸在受力最大時瞬間靜止的狀態。

2.4 解算器的選擇

NX高級仿真支持的線性靜力學分析的解算器主要有NX Nastran-SESTATICS 101，單個約束：該解算類型可以創建具有唯一載荷的子工況，但是每個子工況均使用相同的約束條件；NXNastran-SESTATICS 101，多個約束：該解算類型可以創建多個子工況，每個子工況既包含唯一的載荷又包含唯一的約束，設置不同子工況參數并提交結算作業時，解算器將在一次運行中求解每個子工況。

本文對打緯搖軸采用了分析類型為結構，解算類型為Nastran-SESTATICS101，單個約束的解算方案。

2.5 解算結果及分析

通過NX高級仿真模塊的分析計算，得出圖5的應變云圖和圖6的應力云圖。

由圖5的 Von-Mises應變云圖中可以得出，打緯搖軸發生應變的最大值是在滾輪支架的頂端，位于208014單元，應變的最大值為9.255×10-4mm，另一側位于209530單元的滾輪支架應變值為8.327×10-4mm。

由圖6的馮氏應力云圖中可以看出，應力主要分布在軸體與相鄰臺階面的連接處，軸體與滾輪支架形成的相貫線處，滾輪軸孔的半圓面等易于發生應力集中的區域。其中，應力最大的是軸體與相鄰臺階面的連接處，應力值為206MPa，位于107135單元。表1給出了本次分析的主要結果。

由表1的數據可以看出，打緯搖軸的最大應力206MPa相對于材料的屈服強度835 MPa還是有很大的安全余地的，另外，打緯搖軸的最大應變9.255×10-4mm能夠滿足打緯搖軸在打緯過程中的工藝指標，所以在本文所述的工作條件下，打緯搖軸能夠滿足生產過程中的使用要求。

圖5 打緯搖軸應變云圖

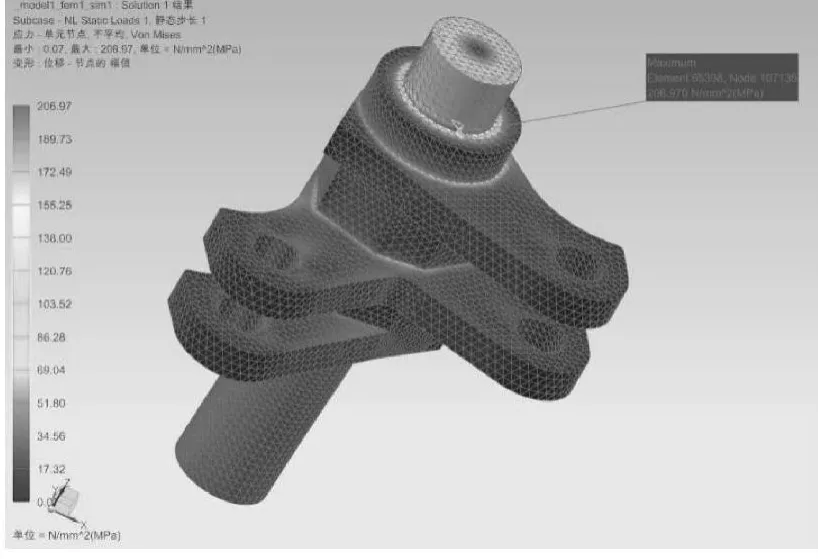
圖6 打緯搖軸馮氏應力云圖

表1 載荷分析結果

3 打緯搖軸模態分析

模態分析是任何涉及非靜力結構設計的一個很重要的部分，用來確保產品和關鍵零部件的固有頻率不會與輸入頻率或者外界強迫作用的頻率一致，這些外界強迫作用是十分常見的。模態分析實質就是將一個彈性連續體的振動問題，離散為一個或者有限個節點位移為廣義坐標的多自由度系統的振動問題，其運動微分方程可以表示為：

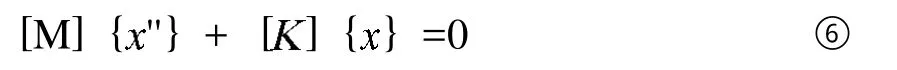
式中，[M]表示構件的總體質量矩陣；[]表示構件的總體剛度矩陣；{}表示節點位移列陣；{''}表示節點位移對時間的二階導數。

上式的解可以假設為如下形式：

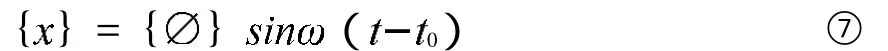
式中，{ }為 階向量； 是向量 的振動頻率； 是時間變量； 是由初始條件確定的時間常數。將式⑦帶入⑥得到如下特征方程：

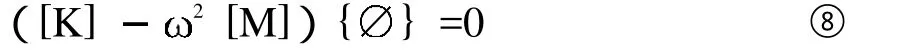
求解上述方程可以確定 和 ，可以得到 個特征值：

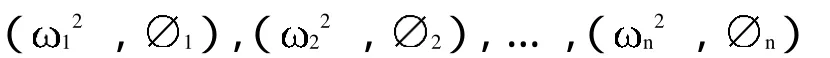
其中，特征值1，2，…，n代表構件的 個固有頻率，或稱為特征頻率，并且滿足：

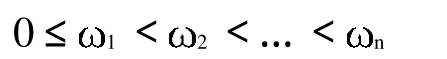
特征向量1，2，…，n代表構件的 個固有振型，對應的幅值可以按照以下確定：

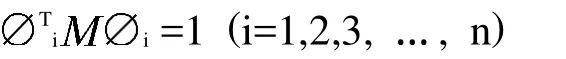
打緯搖軸在打緯過程中會承受周期性載荷的作用，可能會與旋轉的主軸發生強烈的共振，致使動應力急劇的增加，導致打緯搖軸由于扭轉疲勞和彎曲疲勞，在到達其設計壽命之前就被破壞。通常的靜力學計算不能夠完成相關的動力學分析，因此需要對打緯搖軸進行模態分析，從而確定打緯搖軸的固有頻率和振型。

打緯搖軸的固有頻率和振型是設計中的重要參數。通常主軸轉速為400r/min，打緯搖軸轉速略低于主軸轉速，由推算出主軸頻率f=6.667Hz。利用NX Nastran模態分析模塊，計算出打緯搖軸的固有頻率。計算時不考慮阻尼，也與外載荷無關。本文在進行模態計算時，使用了SOL103結算方案。網格劃分與載荷分析相同。

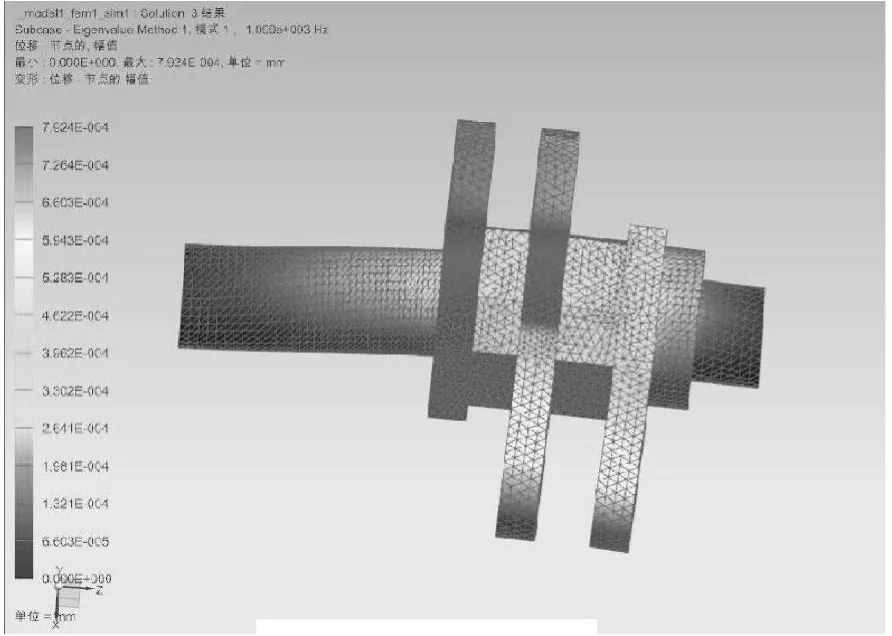
圖7 1階振型

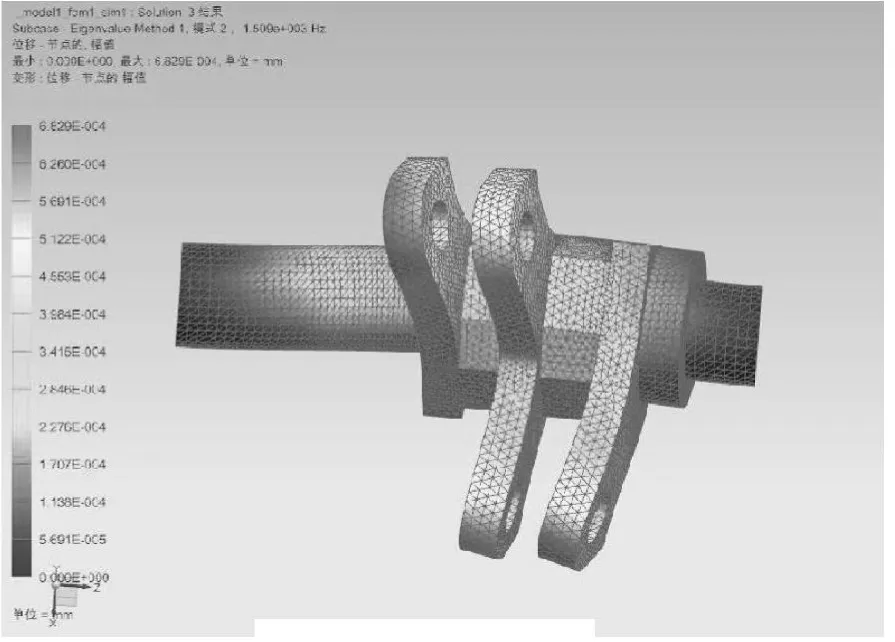
圖8 2階振型

圖9 3階振型

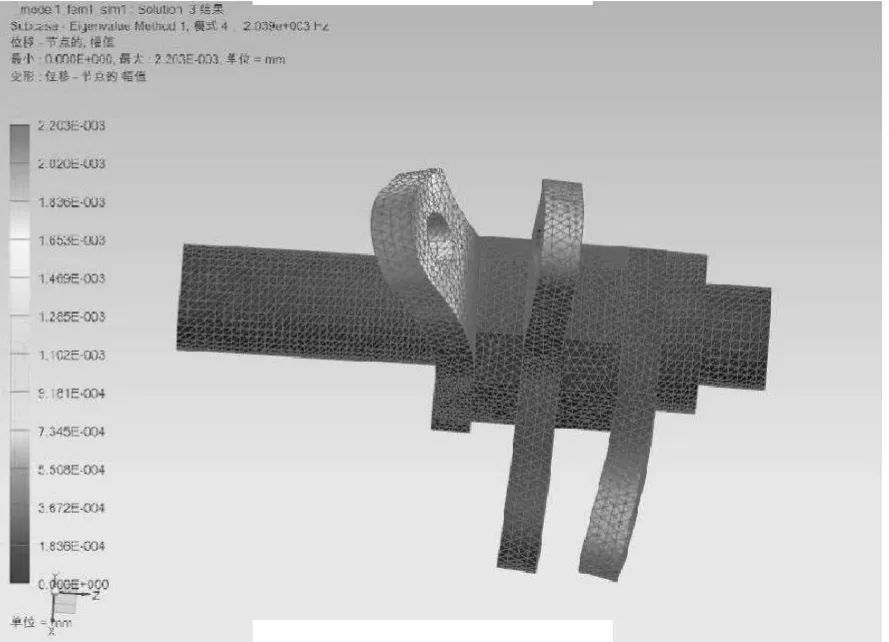
圖10 4階振型

圖11 5階振型

圖12 6階振型

本文取前10階固有頻率和振型，圖7至圖16為打緯搖軸的前10階振型圖。

圖14 8階振型

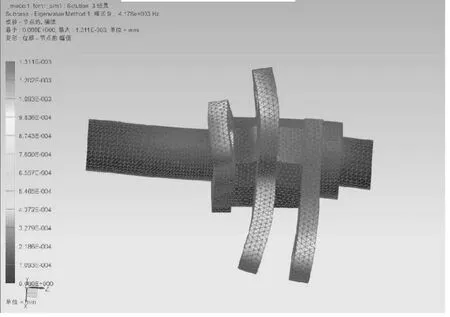
圖15 9階振型

圖16 10階振型

表2為打緯搖軸固有振動頻率和振型分析結果。

表2 打緯搖軸模態計算結果

由模態計算結果可知打緯搖軸自身轉動頻率及主軸轉動頻率遠小于第1階的固有頻率，因此，該打緯搖軸發生共振的可能性很小。

4 打緯搖軸改進措施

通過NX軟件對打緯搖軸進行的載荷計算及模態計算，可以看出疲勞失效是打緯搖軸的主要失效形式。所以需要通過改進設計方案、加工工藝和裝配方法來提高打緯搖軸的使用壽命。可以采取在容易產生應力集中的區域，如軸體與相鄰臺階面的連接處，軸體與滾輪支架形成的相貫線等處進行倒圓角處理；取消原搖軸上的兩組螺孔，改為銑一個平面；除了原先的拉線式組合裝配方法，增加軸承座定位工裝；采用帶有倒角的加工刀具來處理加工面與毛坯面等措施，使打緯搖軸提高使用壽命，并減少在使用過程中因疲勞而造成的失效。

5 結語

本文通過UGNX8.5軟件進行了打緯搖軸的建模，并對其進行了載荷及模態的分析。通過對打緯搖軸的靜應力分析，可知軸體與相鄰臺階面的連接處，軸體與滾輪支架形成的相貫線等處應力比較集中，通過將最大應力與屈服應力進行比較，得知該打緯搖軸的強度能夠滿足生產要求。通過模態分析，得出了打緯搖軸各階的固有頻率和振型，可知該打緯搖軸發生共振的可能性很小。通過對打緯搖軸計算結果的分析，提出了打緯搖軸設計的改進措施，為提高打緯過程的質量，提升劍桿織機的品質提供了一種較為可行的思路。

[1]沈春根，王貴成，王樹林.UG NX 7.0有限元分析入門與實例精講[M].北京：機械工業出版社，2010.

[2]滕兵.高性能劍桿織機打緯和引緯機構的設計與研究[D].上海：東華大學,2006.

[3]陳元甫,洪海滄.劍桿織機原理與使用(第二版)[M].北京：中國紡織出版社,1985.

[4]夏金國.織造機械[M].北京：中國紡織出版社，2001.