油浸倒立式電流互感器主絕緣電場分析與優(yōu)化設(shè)計
閻秀恪 孫 陽 于存湛謝德馨
(1.沈陽工業(yè)大學(xué)電氣工程學(xué)院 沈陽 110870 2.特變電工沈陽變壓器集團有限公司 沈陽 110144 3.遼寧省電力有限公司檢修分公司 沈陽 110003)
1 引言
我國正在建設(shè)大容量、遠(yuǎn)距離、特高壓的堅強國家電網(wǎng),電壓等級的提高,對電網(wǎng)中電氣設(shè)備絕緣可靠性的要求也越來越高。電流互感器作為電網(wǎng)中的重要電氣設(shè)備,一次側(cè)與母線相連,一旦發(fā)生事故,后果非常嚴(yán)重[1,2]。目前電流互感器的發(fā)展趨勢,倒立式電流互感器在國內(nèi)外的應(yīng)用越來越廣泛。該類型產(chǎn)品區(qū)別于傳統(tǒng)的正立式結(jié)構(gòu),將二次繞組與一次繞組集中置于整個產(chǎn)品的上部,避免了正立式結(jié)構(gòu)主絕緣位于產(chǎn)品底部易受潮的環(huán)節(jié),減少了主絕緣因受潮而被擊穿的可能性,但同時也給產(chǎn)品的絕緣設(shè)計和工藝制造增添了一定的難度。倒立式電流互感器根據(jù)其絕緣介質(zhì)的不同又可分為 SF6氣體絕緣和油紙絕緣兩種。近年來,針對 SF6電流互感器電場分析與絕緣優(yōu)化設(shè)計的研究較多[3-5],主要是通過在絕緣瓷套內(nèi)加設(shè)屏蔽罩以及在法蘭外加設(shè)屏蔽環(huán)來改善電場分布。油浸倒立式電流互感器的絕緣結(jié)構(gòu)不同于 SF6電流互感器,通常采用電容型絕緣結(jié)構(gòu),即在絕緣油紙中通過增設(shè)電容屏來改善主絕緣內(nèi)部的電場分布。關(guān)于油浸倒立式電流互感器電場分析與優(yōu)化設(shè)計的研究較少,但實際產(chǎn)品運行事故卻時有發(fā)生,且絕緣事故占有較大比例[6,7]。
油浸倒立式電流互感器增設(shè)電容屏的方法通常分為兩種:一種是在二次側(cè)下引線部位的絕緣油紙中增設(shè)端屏[8,9],這樣只是改善了下引線部分的電場分布,卻忽略了二次側(cè)繞組部位,而該處往往是導(dǎo)致事故發(fā)生的關(guān)鍵部位;另一種則是在整個主絕緣中增設(shè)主電容屏,并且在主屏端部加屏蔽環(huán)以避免尖端放電[10,11]。增設(shè)主屏雖然增加了主絕緣的包扎工藝,卻能夠改善主絕緣整體的電場分布。主屏式結(jié)構(gòu)的油浸倒立式電流互感器結(jié)構(gòu)模型較為特殊,不易達到較高的計算精度,關(guān)于其電場計算與絕緣設(shè)計的研究很少。
本文提出了一個有限元法與解析法相結(jié)合、分層分段計算電場的模型,利用 ANSYS軟件計算一臺220kV主屏式結(jié)構(gòu)油浸倒立式電流互感器的電場分布,并以影響絕緣性能的主要變量——屏間絕緣厚度和屏間梯差作為優(yōu)化變量,采用RBF神經(jīng)網(wǎng)絡(luò)動態(tài)響應(yīng)模型結(jié)合遺傳算法的智能優(yōu)化算法對主屏式絕緣結(jié)構(gòu)進行了優(yōu)化設(shè)計。
2 物理模型
油浸倒立式電流互感器主絕緣結(jié)構(gòu)如圖1所示,整體成倒置的吊環(huán)狀。主電容屏以串聯(lián)形式嵌入主絕緣中,最外層屏接高電位,最內(nèi)層屏接地。相鄰兩個電屏及其中間絕緣部分就構(gòu)成一個電容器,這樣就形成了一個由多個電容器串聯(lián)的回路。
3 電場計算
本文考慮的是油浸倒立式電流互感器在工頻耐壓試驗條件下的電場分布情況,而工頻條件下的電場問題可近似為準(zhǔn)靜態(tài)場問題[12,13],靜電場對應(yīng)的邊值問題為

式中, V(I)為每層電屏的電位,由該層屏間電容C(I)串聯(lián)分壓求得
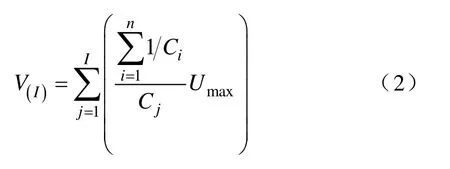
屏間電容C(I)可以由數(shù)值法和解析法求得。
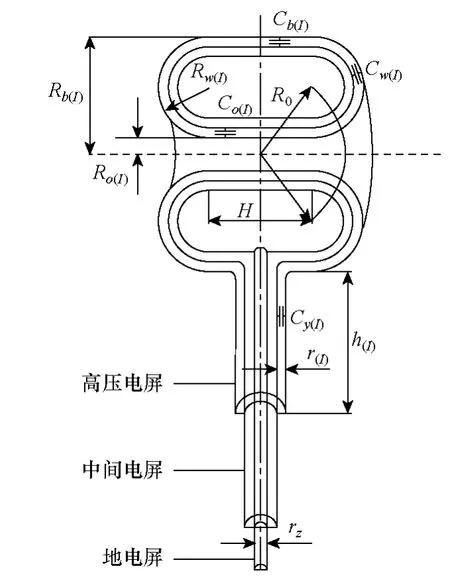
圖1 油浸倒立式電流互感器主絕緣結(jié)構(gòu)示意圖Fig.1 Main insulation of oil-immersed inverted current transformer
以本文計算的220kV油浸倒立式電流互感器為例,由于采用主屏式絕緣結(jié)構(gòu),主絕緣中設(shè)置多個電容屏,各屏間絕緣厚度大約在0~20mm之間,而主絕緣從上端環(huán)部到下端引線部,整體高度接近4m,尺寸相差很大,如果整體采用三維有限元計算,單元剖分無法達到較高的計算精度。因此本文將模型分層分段處理,將環(huán)部與下引線部分分開,又將環(huán)部的每一層分開,針對每層取四分之一建立三維模型,計算三維電場分布;對于下引線部分,基于其軸對稱結(jié)構(gòu),進行二維電場有限元分析。
3.1 解析法求解電容

如圖1所示,屏間電容 C(I)由環(huán)部電容 Ch(I)和引線電容Cy(I)并聯(lián)組成式中,環(huán)部電容 Ch(I)又由內(nèi)圓筒電容 Ca(I)、外圓筒電容Cb(I)和拐彎處電容Cw(I)并聯(lián)組成。而環(huán)部和下引線之間過渡部分的電容不易確定,采取在外圓筒電容中減去與引線重疊部分的電容 Cs(I)的方法來等效,如圖2所示。
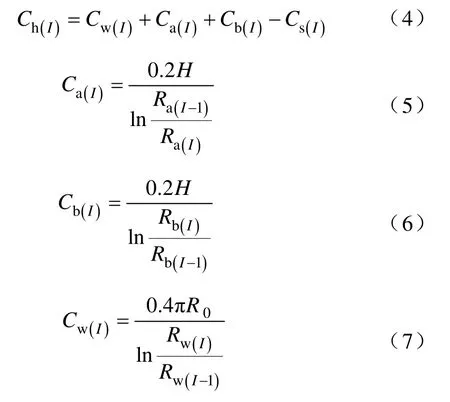
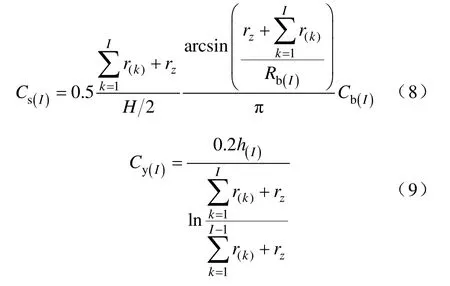
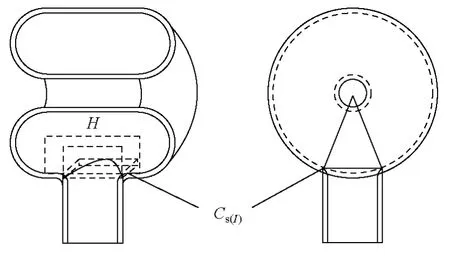
圖2 等效電容示意圖Fig.2 Equivalent capacitance sketch
3.2 數(shù)值法求解電容
屏間電容也可以由有限元法計算得到,基于ANSYS軟件將整個主絕緣按其屏間絕緣厚度分層建立模型,將各層絕緣的表面視為電容屏,單獨計算各層屏間電容,選取相鄰兩個電容屏上的節(jié)點定義成組件,以內(nèi)屏為地,利用CMATRIX宏命令求解。
3.3 實例分析
本文以一臺 220kV油浸倒立式電流互感器為例,計算電場分布,其主要參數(shù)見表1。
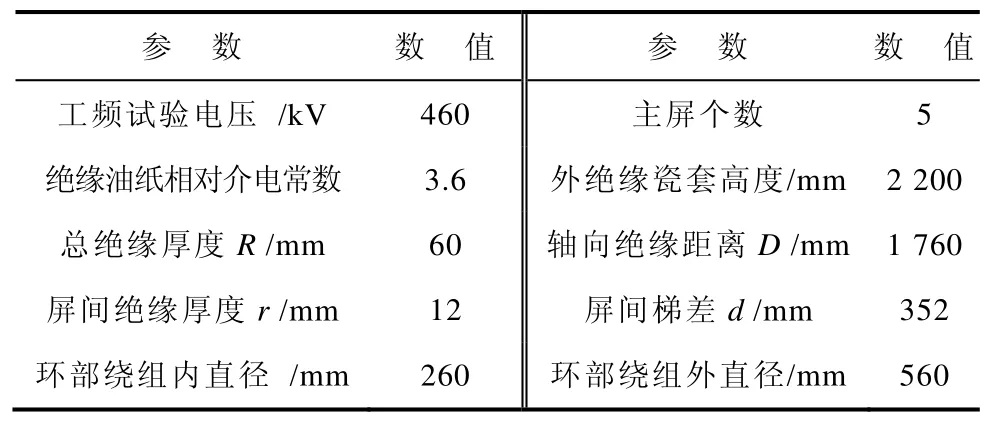
表1 互感器主要參數(shù)Tab.1 Parameters of the current transformer
其中屏間絕緣厚度和屏間梯差等變量如圖3所示。本文按照工程慣例,五個主屏間的絕緣厚度和梯差按均值情況計算,之后對其進行優(yōu)化設(shè)計。分別采用解析法與數(shù)值法計算屏間電容,結(jié)果見表2。
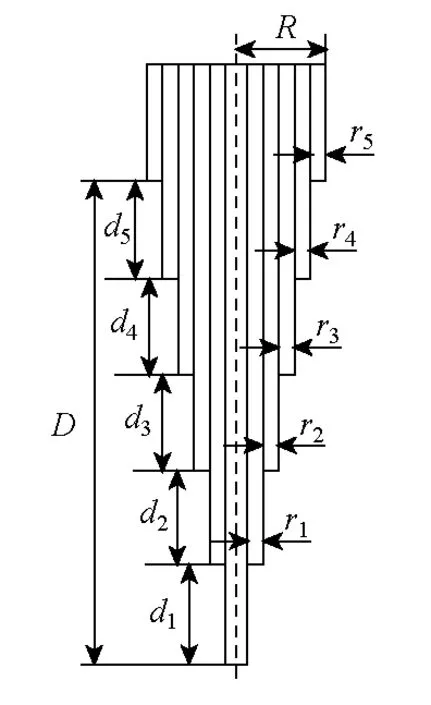
圖3 屏間絕緣厚度和屏間梯差示意圖Fig.3 Sketch of thickness and gradient difference between two adjacent screens
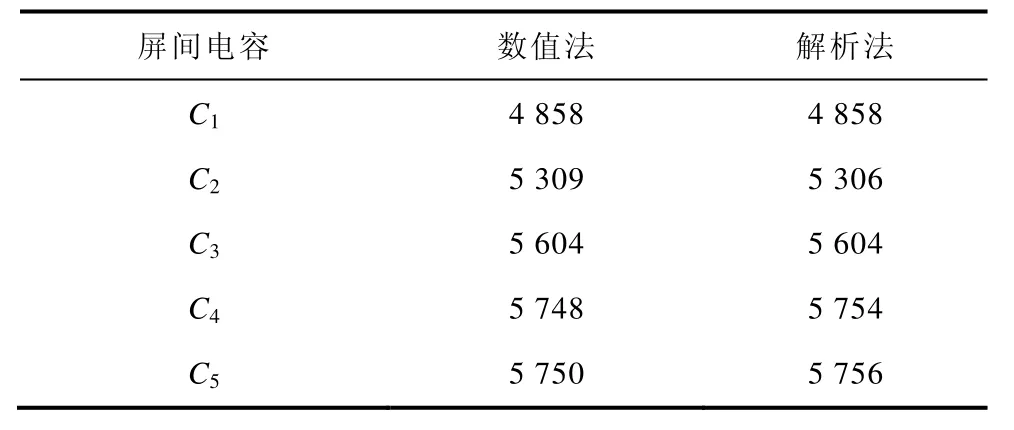
表2 兩種求解屏間電容方法的對比Tab.2 Comparison between two methods for capacitance calculation (單位: pF)
由表2可以看出,兩種方法的計算結(jié)果基本一致,本文采用解析法對屏間電容的計算具有足夠的精度和可行性。
由屏間電容串聯(lián)分壓得到各屏激勵電位,利用ANSYS軟件對環(huán)部各層和引線部分分別建模并進行有限元計算。圖4為環(huán)部一層的三維網(wǎng)格剖分圖,可以看出,網(wǎng)格細(xì)密而均勻,如果將電流互感器整體進行三維剖分,無法達到這樣的精度。

圖4 環(huán)部一層網(wǎng)格剖分圖Fig.4 The 3D meshes of one layer of central loop
通過可視化處理,計算得到的環(huán)部各層絕緣的電場分布基本相同,整體趨勢由內(nèi)向外逐漸降低。圖5為電場強度最大的第一層(最內(nèi)層)絕緣環(huán)部的電場分布,其余四層類同,不再列出。
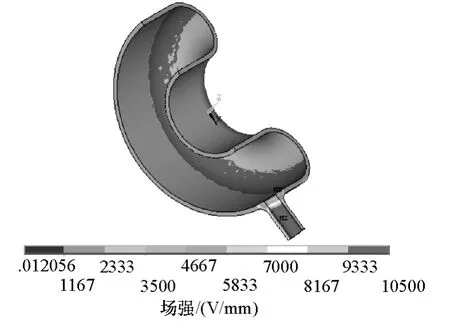
圖5 環(huán)部第一層電場分布Fig.5 Electric field distribution of the first layer of central loop
可以看出,油浸倒立式電流互感器環(huán)部的電場較為集中在各層內(nèi)圓筒與外圓筒交接的環(huán)型部位的內(nèi)表面和下引線部分的內(nèi)表面,其場強最大值位于下引線內(nèi)表面,為10 500V/mm。
下引線部分電場分布的整體趨勢與環(huán)部相同,電場較為集中在端環(huán)表面和各層電容屏表面,如圖6所示,最大值為10 495V/mm。
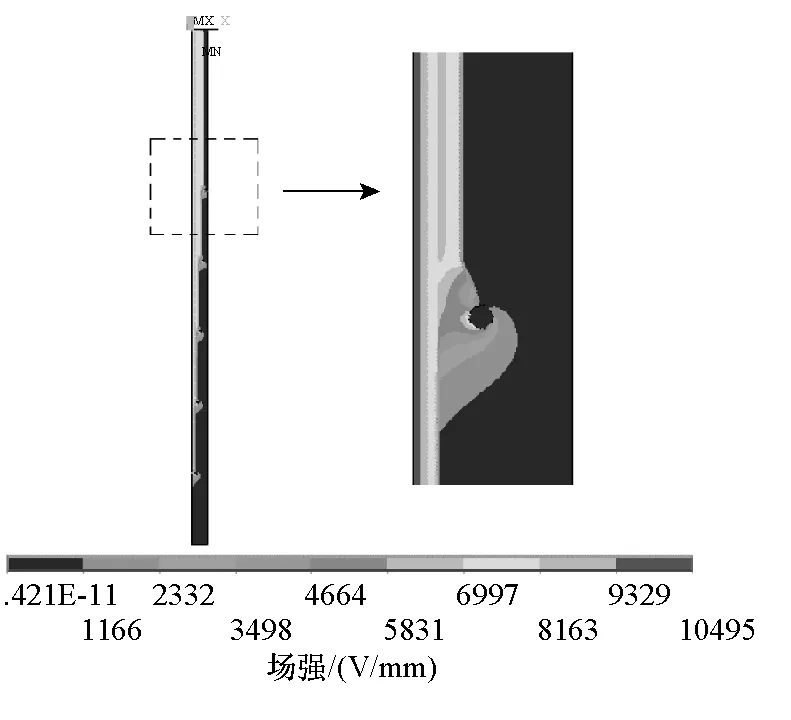
圖6 下引線及端環(huán)附近電場分布Fig.6 Electric field distribution of down-lead and shielding ring
電流互感器環(huán)部三維電場計算與下引線二維電場計算得到的場強最大值均位于下引線最內(nèi)層屏表面的同一位置,圖5和圖6中最大場強的微小誤差源于三維剖分與二維剖分的差異。
基于電流互感器環(huán)部與下引線的結(jié)構(gòu)特征,其場強可視作呈徑向分布,因此工程上通常關(guān)注其徑向電場強度[8],徑向場強可由下式計算
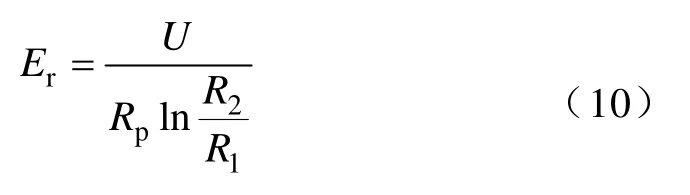
式中 U——屏間電壓;
Rp——計算位置的半徑;
R1——內(nèi)屏半徑;
R2——外屏半徑。
按上式計算下引線部分各屏表面的電場強度,得到各層最大場強。由有限元法計算得到各層絕緣最大電場強度的離散解,將計算結(jié)果進行比較見表3。兩種方法的計算結(jié)果基本一致,驗證了本文提出的分層分段計算的有限元模型的精度和可行性。
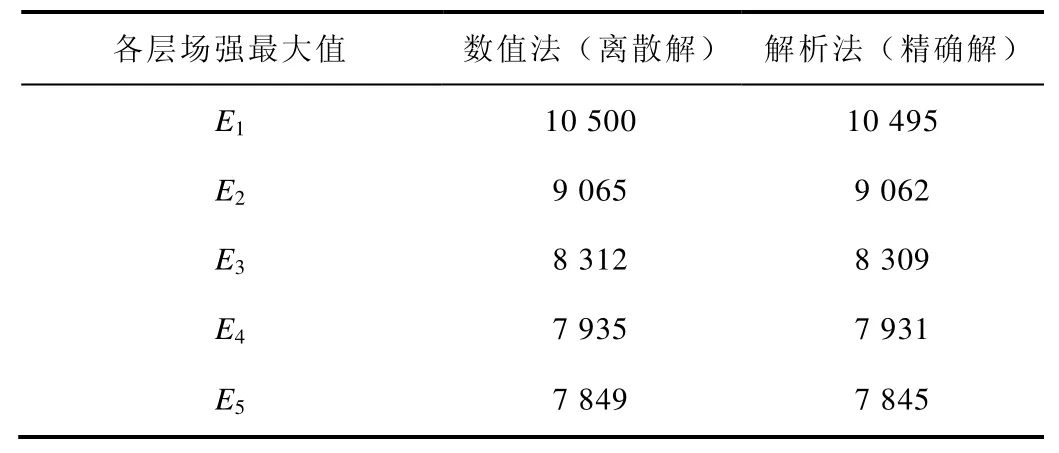
表3 均值情況下各層絕緣電場強度最大值Tab.3 Maximum electric intensity of each layer insulation(單位: V/mm)
4 主絕緣優(yōu)化設(shè)計
4.1 影響絕緣性能的主要因素
由于采用電容型絕緣結(jié)構(gòu),電容屏的數(shù)量、長短、位置就成為絕緣設(shè)計的關(guān)鍵。工程上通常為了設(shè)計方便和制作工藝簡單,電容屏設(shè)計采用等絕緣厚度、等梯差原則,但這并不意味著均值情況為最佳選擇。屏間絕緣厚度影響絕緣效果,理想情況是屏間絕緣厚度盡可能的小[9],但會導(dǎo)致主屏個數(shù)的增加,提高了生產(chǎn)成本和絕緣包扎的難度。而在屏數(shù)恒定的情況下調(diào)整屏間絕緣厚度和梯差可以改善電場分布,這就意味著在成本不變的情況下,提高了產(chǎn)品的絕緣可靠性。
4.2 優(yōu)化模型與參數(shù)設(shè)計
因此,本文在主屏個數(shù)恒定,總絕緣厚度和總梯差一定的條件下,以各屏間絕緣厚度和屏間梯差為優(yōu)化變量,以最大電場強度為目標(biāo)函數(shù)對主絕緣結(jié)構(gòu)進行優(yōu)化設(shè)計。優(yōu)化計算模型為
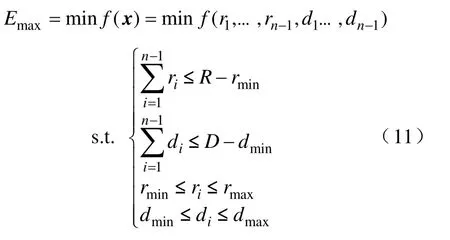
式中 n——電流互感器主屏個數(shù);
R——總絕緣厚度;
D——總梯差;
ri——各層屏間絕緣厚度;
di——屏間梯差;
rmin,rmax——屏間絕緣厚度和的上、下限;
dmin,dmax——屏間梯差的上、下限。
多次的計算和分析表明,屏間絕緣厚度對屏間電壓分布的不均勻度影響較大,同時端環(huán)表面的電場強度又和該端環(huán)處屏間電壓密切相關(guān),繼而影響電場分布。另外考慮到制造工藝的限制,本文對所研究電流互感器的優(yōu)化變量的變化范圍設(shè)定如下:
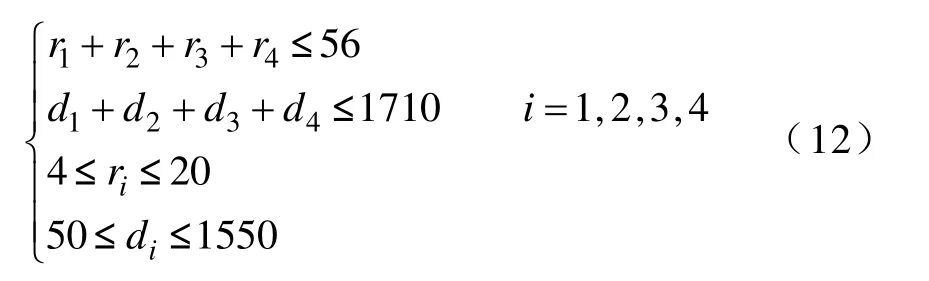
4.3 優(yōu)化過程
由于優(yōu)化設(shè)計變量較多,電場分析計算量大,采用單一的隨機類優(yōu)化算法會消耗大量的系統(tǒng)資源和計算時間,因此本文采用基于徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡(luò)動態(tài)響應(yīng)模型[14-19]結(jié)合遺傳算法的優(yōu)化策略。即在滿足約束條件的樣本空間中,采用RBF神經(jīng)網(wǎng)絡(luò)建立響應(yīng)模型,重構(gòu)目標(biāo)函數(shù)。在樣本空間中采用遺傳算法尋優(yōu),種群個體的目標(biāo)函數(shù)值由重構(gòu)目標(biāo)函數(shù)計算得到。而樣本空間和響應(yīng)模型則跟隨每次迭代的最優(yōu)點的位置不斷更新、細(xì)化,具體策略如下:
(1)以主絕緣中的最大電場強度為目標(biāo)函數(shù),采用本文提出的電場計算模型,由解析法計算屏間電容及各屏的激勵電位,由有限元模型計算主絕緣電場分布,得到最大場強。
(2)確定滿足優(yōu)化變量約束條件的初始采樣空間,離散采樣空間,隨機采樣。
(3)將樣本點(即主絕緣設(shè)計方案)載入步驟(1)中的電場計算模型,計算其目標(biāo)函數(shù)值。
(4)將樣本點及對應(yīng)的目標(biāo)函數(shù)值帶入 RBF神經(jīng)網(wǎng)絡(luò)中,通過學(xué)習(xí)訓(xùn)練得出重構(gòu)目標(biāo)函數(shù),確定響應(yīng)模型。
(5)在采樣空間中生成遺傳算法的初始種群,通過進化尋優(yōu)得到當(dāng)前的最優(yōu)點,尋優(yōu)過程中個體的目標(biāo)函數(shù)值由重構(gòu)目標(biāo)函數(shù)計算得到,無須進行有限元計算,大大減少了計算成本。
(6)將步驟(5)中由遺傳算法得到的最優(yōu)點載入步驟(1)中的電場計算模型,計算其目標(biāo)函數(shù)值,并與上一次的最優(yōu)點相比較,判斷是否滿足如下收斂條件

若滿足,則 xk為最優(yōu)解(即最優(yōu)設(shè)計方案),迭代結(jié)束,輸出最優(yōu)方案,否則跳至下一步(其中ε1、ε2為設(shè)定的誤差)。
(7)以當(dāng)前最優(yōu)點為中心將采樣空間縮小0.618倍。
(8)提高精度離散采樣空間,隨機采樣,返回步驟(4)。
4.4 優(yōu)化結(jié)果
通過上述優(yōu)化過程的迭代計算,最終得到最優(yōu)方案見表4。
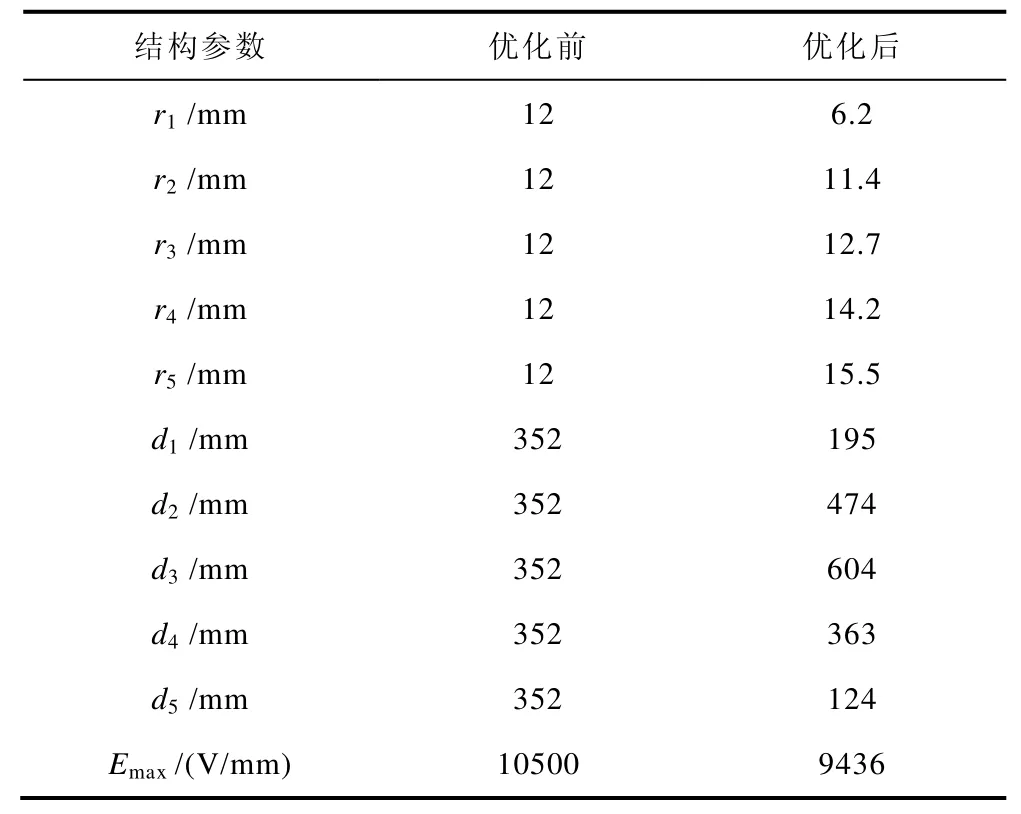
表4 優(yōu)化結(jié)果Tab.4 Optimization results
由表4可以看出,最優(yōu)方案的主絕緣最大電場強度降低了 10.1%。方案中屏間絕緣厚度由內(nèi)向外逐漸增加,最內(nèi)層屏間絕緣厚度相對較小,其它屏間絕緣厚度均勻遞增。而屏間梯差由內(nèi)向外呈現(xiàn)先增后減的趨勢,這為油浸倒立式電流互感器的設(shè)計和制造提供了指導(dǎo)和參考。
圖7和圖8分別為優(yōu)化后主絕緣環(huán)部第一層和引線部分的電場分布。
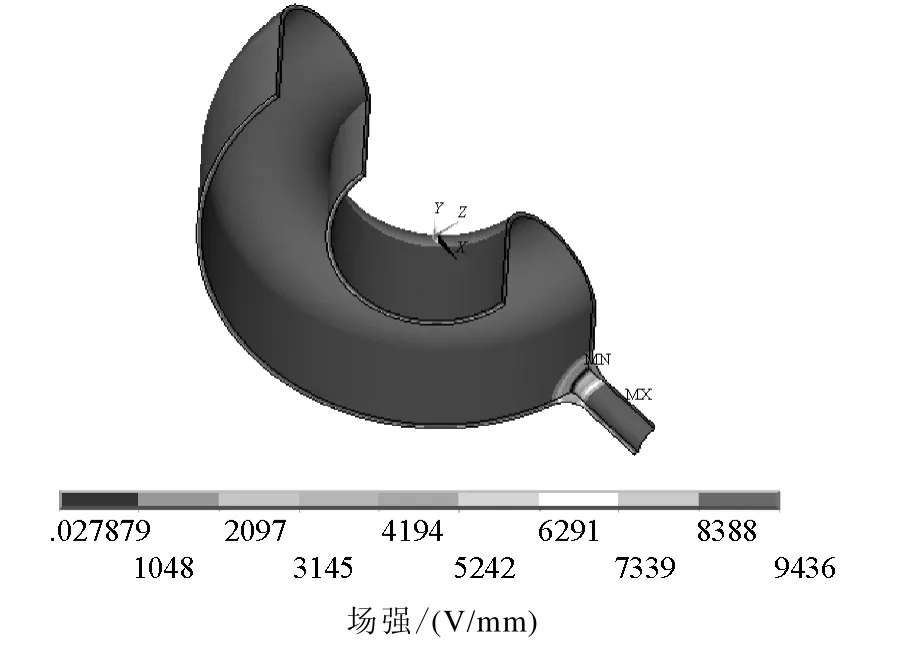
圖7 環(huán)部第一層電場分布(優(yōu)化后)Fig.7 The electric field distribution of the first layer of central loop(after optimization)
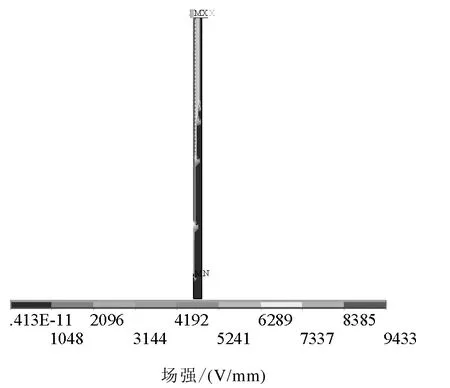
圖8 引線部分電場分布(優(yōu)化后)Fig.8 The electric field distribution of down-lead(after optimization)
由上面兩圖可以看出,優(yōu)化后不僅電場強度降低了,主絕緣中的電場分布也更為均勻了。
5 結(jié)論
本文針對主屏式結(jié)構(gòu)油浸倒立式電流互感器的結(jié)構(gòu)特點,提出有限元法與解析法相結(jié)合的電場計算模型,分層分段計算了主絕緣中的電場分布。在電場分析的基礎(chǔ)上,以各主屏屏間絕緣厚度和屏間梯差為優(yōu)化變量,對主絕緣結(jié)構(gòu)進行了優(yōu)化設(shè)計。優(yōu)化方案表明,屏間絕緣厚度由內(nèi)至外逐漸增加、屏間梯差由內(nèi)向外先增后減的設(shè)計,將使主絕緣內(nèi)的電場強度降低,電場分布更加均勻,這為油浸倒立式電流互感器的設(shè)計和制造提供了理論指導(dǎo)和設(shè)計參考。
[1] 王世閣.倒置式電流互感器運行狀況分析及提高安全運行性能的建議[J].變壓器,2009,46(9): 64-68.Wang Shige.Operation analysis of inverted current transformer and suggestion to improve operational safety[J].Transformer,2009,46(9): 64-68.
[2] Satish M Mahajan,Diego M Robalino.Thermal modeling of an inverted-type oil-immersed current transformer [J].IEEE Transactions on Power Delivery,2010,25(4): 2511-2518.
[3] 王仲弈,馬志瀛,顧沈卉,等.550kV SF6絕緣電流互感器的電場計算分析[J].華北電力大學(xué)學(xué)報,2005,23(sup): 71-74.Wang Zhongyi,Ma Zhiying,Gu Shenhui,et al.Electric field calculation and analysis of 550kV SF6current transformer[J].Journal of North China Electric Power University,2005,23(sup): 71-74.
[4] 王世山,李彥明,佟威,等.SF6電流互感器電場計算及其結(jié)構(gòu)優(yōu)化[J].電瓷避雷器,2003(4): 22-24.Wang Shishan,Li Yanming,Tong Wei,et al.Electric stress calculation and design optimization of SF6current transformer[J].Nsulators and Surge Arresters,2003(4): 22-24.
[5] 羅青林,劉玉鳳,330kV SF6電流互感器電場計算及絕緣結(jié)構(gòu)分析[J].變壓器,2001,38(4): 16-19.Luo Qinglin,Liu Yufeng.Calculation of electric field in a 330kV SF6current transformer and its insulation structure analysis[J].Transformer,2001,38(4):16-19.
[6] 鄒彬,郭森,袁聰波,等.一起 220kV 油浸倒立式電流互感器故障原因分析[J].變壓器,2010,47(2):69-71.Zou Bin,Guo Sen,Yuan Congbo,et al.Fault analysis of 220kV oil-immersed inverter-type current transformer[J].Transformer,2010,47(2): 69-71.
[7] 陳瑞國,韓洪剛,孫艷鶴.220kV油浸倒立式電流互感器故障原因分析[J].變壓器,2010,47(5): 68-71.Chen Ruiguo,Han Honggang,Sun Yanhe.Problem analysis of 220kV oil-immersed inverter-type current transformer[J].Transformer,2010,47(5): 68-71.
[8] 尚耀輝,趙建洲,劉亞亞,等.絕緣油紙電流互感器的絕緣設(shè)計[J].電力電容器與無功補償,2009,30(3):25-27.Shang Yaohui,Zhao Jianzhou,Liu Yaya,et al.The insulation design of oil-paper insulation current transformer[J].Power Capacitor & Reactive Power Compensation,2009,30(3): 25-27.
[9] 魏朝暉.油浸倒立式電流互感器設(shè)計[J].變壓器,2000,37(9): 6-9.Wei Zhaohui.Design of oil immersed inverted current transformer[J].Transformer,2000,37(9): 6-9.
[10] 互感器制造技術(shù)編審委員會.互感器制造技術(shù)[M].北京: 機械工業(yè)出版社,1998.
[11] 肖耀榮,高祖綿.互感器原理與設(shè)計基礎(chǔ)[M].沈陽:遼寧科學(xué)技術(shù)出版社,2003.
[12] 楊茜,郭天興,劉海,等.110kV電流互感器電場分析與絕緣結(jié)構(gòu)改進[J].電力電容器與無功補償,2010,31(1): 31-34.Yang Qian,Guo Tianxing,Liu Hai,et al.Electric field analysis and insulation structure improvement for 110kV current transformer[J].Power Capacitor &Reactive Power Compensation,2010,31(1): 31-34.
[13] 馬愛清,鄭勇,江秀臣,等.MPCG算法在GIS三相共罐式 SF6高壓斷路器電場計算中的應(yīng)用[J].中國電機工程學(xué)報,2007,27(24): 5-10.Ma Aiqing,Zheng Yong,Jiang Xiuchen,et al.Application of MPCG aligorithm to three dimensional electric field calculation of SF6circuit breaker in three-phase-in-one-tank GIS[J].Proceedings of the CSEE,2007,27(24): 5-10.
[14] 曹云東,劉曉明,劉冬,等.動態(tài)神經(jīng)網(wǎng)絡(luò)法及在多變量電器優(yōu)化設(shè)計中的研究[J].中國電機工程學(xué)報,2006,26(8): 112-116.Cao Yundong,Liu Xiaoming,Liu Dong,et al.Investigation of a dynamic nerual network approach and its application of multivariable optimization to electric apparatus[J].Proceedings of the CSEE,2006,26(8): 112-116.
[15] 李巖,王東風(fēng),焦嵩鳴,等.采用微分進化算法和徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)的熱工過程模型辨識[J].中國電機工程學(xué)報,2010,30(8): 110-116.Li Yan,Wang Dongfeng,Jiao Songming,et al.Thermal process identification using differential evolution algorith and radial basis function neural network[J].Proceedings of the CSEE,2010,30(8):110-116.
[16] Chang G W,Chen Cheng I,Teng Yu Feng.Radialbasis-function-based neural network for harmonic detection[J].IEEE Transactions on Industrial Electronics,2010,57(6): 2171-2179.
[17] S Gholizadeh,E Salajegheh,P Torkzadeh.Structural optimization with frequency constraints by genetic algorithm using wavelet radial basis function neural network[J].Journal of Sound and Vibration,2008,312(1-2): 316-331.
[18] JBarry Gomm,Ding Li Yu.Selecting radial basis function network centers with recursive orthogonal least squares training[J].IEEE Transactions on Neural Networks,2000,11(2):306-314.
[19] 桂勁松,康海貴.結(jié)構(gòu)可靠度分析的改進 BP神經(jīng)網(wǎng)絡(luò)響應(yīng)面法[J].應(yīng)用力學(xué)學(xué)報,2005,22(1):127-130.Gui Jinsong,Kang Haigui.Improved BP ANN response surface method for structural relibility analysis[J].Chinese Journal of Applied Mechanics,2005,22(1): 127-130.

