淺海溫躍層對水聲傳播損失場的影響

潘長明，高飛，，孫磊，3，王璐華，王本洪，李璨

(1.海軍海洋測繪研究所儀器設備研究室，天津300061;2.解放軍理工大學氣象海洋學院，江蘇南京211101;3.哈爾濱工程大學水聲工程學院，黑龍江哈爾濱150001)

水聲調查資料在海洋工程、海洋科學和軍事海洋環境保障方面有廣泛的應用前景[1]。因此開展水聲調查研究，特別是溫鹽躍層對淺海聲場的分布和傳播影響的探索有著重要的科學意義和應用價值。水聲傳播損失一般分為擴展損失和衰減損失，后者是由于傳播媒介的吸收、散射等作用造成，因此必然受到海洋環境的影響。溫躍層[2]是重要的海洋現象，其對聲場傳播影響顯著已被許多學者證實[3-6]。

聲波在淺海和深海中的傳播性質存在明顯差異，躍層的影響作用各異，本文重點研究淺海溫躍層對水聲傳播的影響。BAO等[7](1994)利用在黃海南部進行的聲學試驗得出淺海水體密度主要取決于溫度。Martine等(2004)[8]對比分析 Kauai(夏季)和Elba(冬季)水聲傳播的差異，得出溫躍層和海底地質對聲場傳播的影響。Lin Zhang等(2012)[9]等利用束狀射線理論模型RAY研究了溫躍層對水聲傳播的影響。張旭等(2012)[10]通過模擬中國近海陸架海區躍層強度變化和不同季節躍層位置變化，結合Kraken模型對淺海聲信道的能量場分布進行了研究。北太平洋聲學實驗室成員(2012)[11]對北菲律賓海深海水聲傳播和環境噪音的影響進行一系列研究，獲得了深海聲線傳播時間與溫躍層季節變化的關系。過去研究溫躍層對水聲場的影響以模擬仿真為主，存在聲學模型本身的制約;部分利用聲學調查數據也是單航次資料，無法進行溫躍層季節性變化對比;同時沒能很好的將模式研究和實測資料結合起來。

針對傳統研究中調查數據的不足，模型模擬的理想性等限制，本文將2007、2008、2009年3個航次的聲學調查實測數據和UMPE拋物方程水聲模式有機結合，通過分析確定溫躍層的位置、深度和厚度以及季節變化等因素，同時綜合考慮海表、海底、水體狀況，來分析溫度躍層結構對淺海聲傳播的影響效應。

1 淺海聲學調查

聲學調查3個航次時間分別為2007年07月、2008年04月、2009年09月。其中3個航次的觀測方案、觀測區域和走航斷面、實驗儀器大致相同，下面以2009年調查為例進行說明。整個調查海區的調查以走航觀測與定點觀測相結合的方式進行，調查項目包含聲傳播損失、海洋環境噪聲、GPS數據、溫度、鹽度、密度、水深、海面氣象和海表風浪等，示意圖如圖1。

水聲探測浮標系統，能接收不同距離處爆炸聲源和人工聲源在20 Hz～10 kHz頻帶內不同中心頻率下的水聲信號，給出工作船和浮標接收系統的數據記錄。通過海面浮標下掛水聽器陣(含8個不同深度的水聽器)，接收位于相對溫躍層不同深度的聲波，采用通信控制為主，自動作業方式為輔的工作方式。某型拖曳聲源，是專門為海洋聲傳播損失測量和海底特性調查設計的人工聲源，是一種近似無指向性聲源，能提供人工控制(或自動)發射多種波形的大功率聲波信號。本航次聲源發射頻率為0.58、1.3 和 6.3 kHz，含正弦波、線性調頻波，實時顯示拖魚的GPS坐標和入水深度。

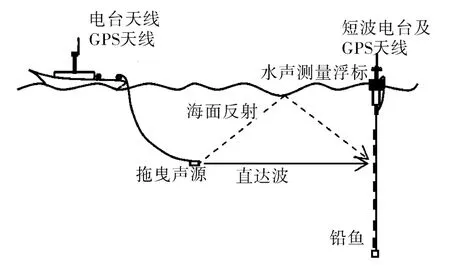
圖1 聲學調查示意圖Fig.1 Sketch map of acoustic research

利用CTD、XBT測得觀測斷面上的溫度、鹽度、密度，計算出聲速剖面，利用多波束沿發射航線測深。關注海表氣象情況，主要包括風、降水等;海區水文概況，主要包括海流、潮流，海浪等。調查海區海底地形相對平坦，最大水深為84.0 m，最淺水深52.0 m，海底地型以沙和泥沙為主，如圖2。同時，對作業海區進行實時天氣預報，主要包括海面天氣、風速、風向、浪高等。

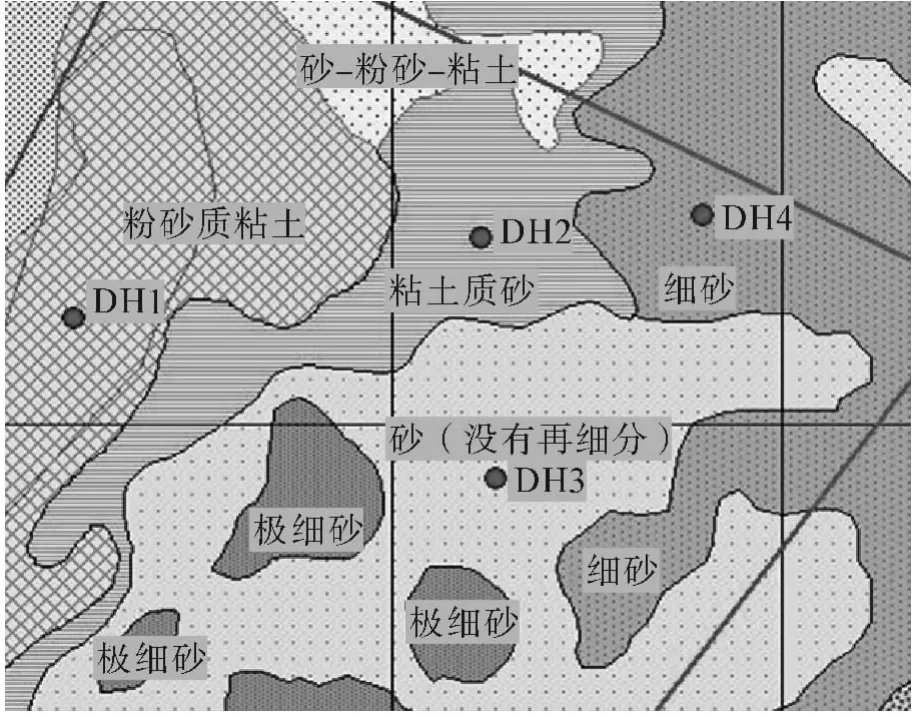
圖2 調查海區底質分布圖Fig.2 Sketch map of bottom shelf in research area

2 UMPE模型

為討論實際淺海中溫躍層的時空變化對海洋聲場的影響，引入UMPE(the University of Miami parabolic equation)拋物方程數值模式對聲場傳播損失進行模擬。UMPE模型[12]是由邁阿密大學和美國海軍研究院聯合開發的一種海洋水聲模型。拋物方程方法由Tappert F D引入到水下聲學傳播衰減的研究，其研發的聲場數值模型稱作拋物方程模型(PE models)[13-14]。該模式靈活性大、適應性強，可通過參數文件來控制海表、海底條件，需計算的水平距離和垂直深度，輸出所需的結果文件。對遠距離的傳播衰減模擬效果較好[9]。柱坐標系下的Helmholtz 方程為[12，15]

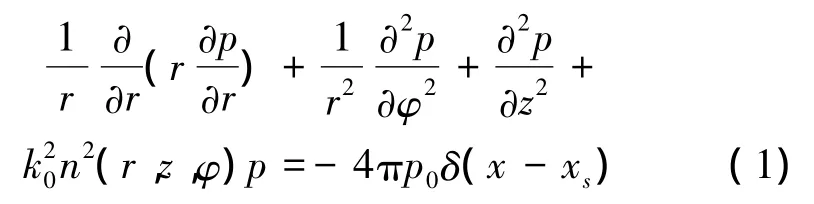
式中:r為距離;ω 為圓頻率;z為水深;p(r，z，φ，ωt)為聲壓，等于 p(r，z，φ )e-ωt;k0= ω /c0為參考波數;n(r，z，φ)=c0/c(r，z，φ)是聲學折射率參數，c(r，z，φ)為聲速;zs為聲源所在深度;xs為點(r=0，z=zs)。設波解形式為

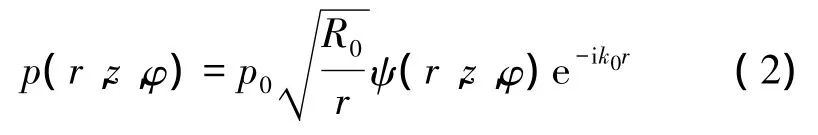
當r=R0時，ψ=1，p=p0，經過計算可得到ψ滿足偏微分方程為

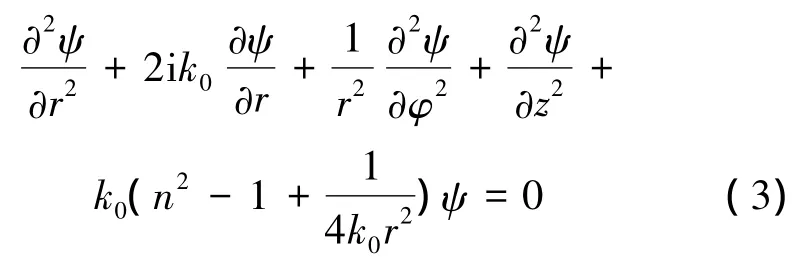
針對擬計算的近海聲場近似，對上式做近似簡化處理，略去含有和的項，于是式(3)可以化為，即拋物型方程模型[13-14]:

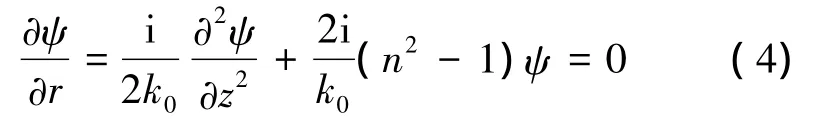
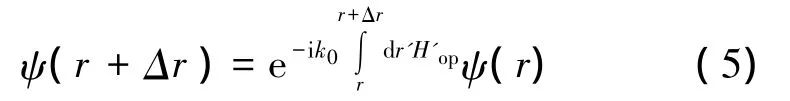
將式(5)代入聲壓表達式(2)，計算出聲壓場。

3 實測數據研究

3.1 水聽器深度及聲源頻率的影響

水聲信道傳播能力強弱受到水深、海底、海表、水體水文要素的綜合作用。研究溫躍層對水聲場的影響首先要確定水聽器與聲源的相對位置，以及水深等要素對水聲場的影響。如圖3，其中發射頻率0.58、1.3、6.3 kHz 對應的聲源級分別為 188、188.3、190.5 dB，帶寬統一為500 ms。淺海水深較淺，通過實測數據的對比分析發現，正躍層條件下深層的水聽器接收到的聲能較大，接近海表的水聽器接收到的聲能相對最小(如圖3)。

根據聲線在介質中傳播總是彎向聲速較小的方向，說明在淺海海域聲波在經過多次反射之后，波動振幅逐漸減小，趨于平滑，同時向海底匯聚。圖4中6.3 kHz接收到的聲能曲線較短，同時傳播損失較大，這驗證了高頻聲波在傳播過程中衰減較快，傳播距離較短。

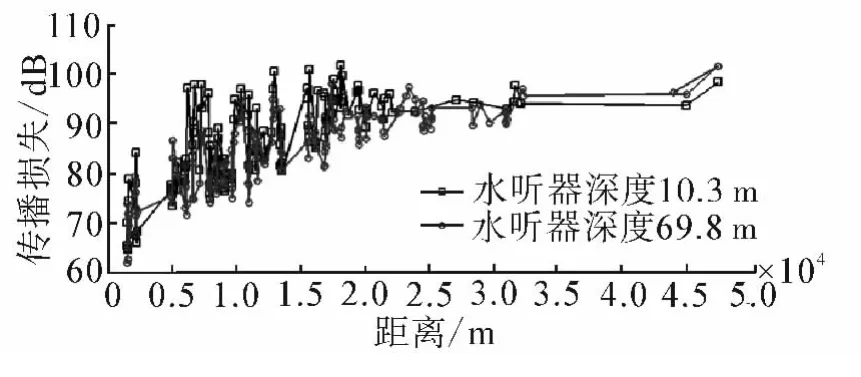
圖3 不同深度水聽器傳播損失對比Fig.3 The TL comparison between hydrophones of different depths

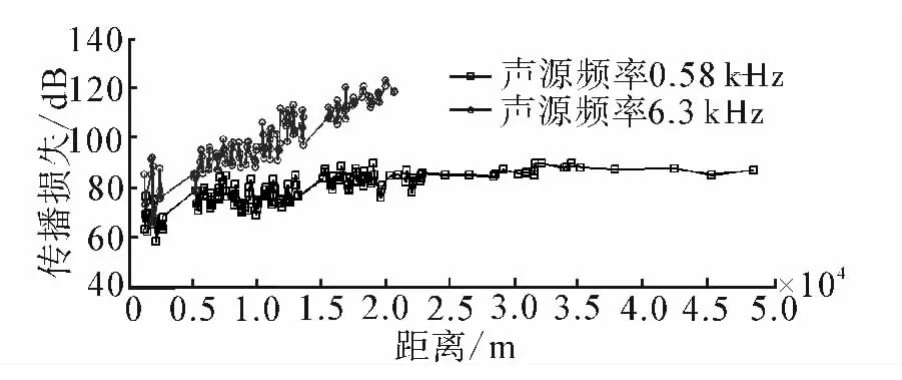
圖4 不同頻率傳播損失對比Fig.4 The TL comparison between different frequencies

3.2 溫躍層時空特征

對夏、春2個季節溫度剖面進行分析，得出溫躍層存在的差異，進而研究溫躍層對水聲場的影響。東海近海春季海表開始增溫，存在較弱的垂直溫度梯度，依據國家海洋調查規范[16]，淺海(水深小于200 m)躍層判定標準為 0.5°C·m-1，該海域還尚未達到溫躍層標準;夏季溫躍層最大強度在0.5°C·m-1以上，溫躍層上界深度在20 m左右[17]。受數據限制，分別對4月(春)、9月(夏)該海域相同位置處走航調查測得的溫度斷面進行對比分析。將溫度數據進行垂向Akima插值處理到垂直間隔1 m的層次，利用垂直梯度法判定溫躍層:

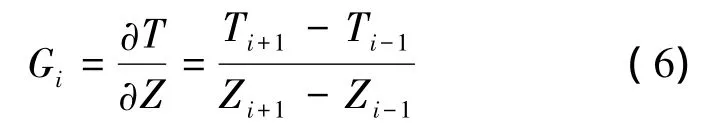
同時，聲速計算采用Wilson于1960年導出的聲速公式[18]:

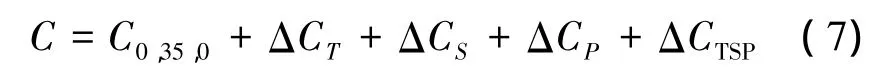
式中:Gi為溫度梯度，i為序列號，Ti為第i層溫度，Zi為第 i層深度。其中 C0，35，0=1 492.9 m·s-1，溫度-4°C＜T＜30°C，壓力 1 kg·cm-2＜P＜1 000 kg·cm-2，鹽度 0＜S＜37，計算精度較高，適合我國海區。

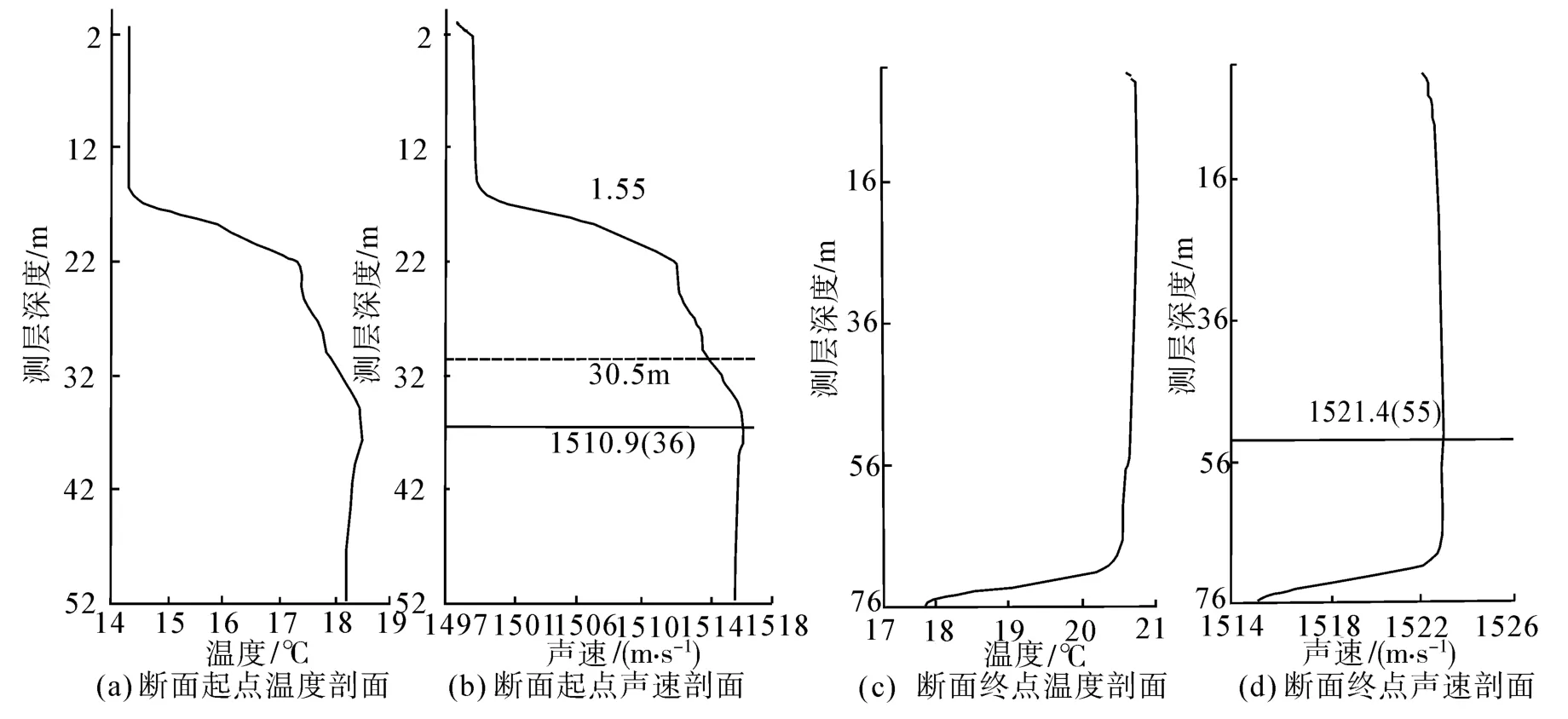
圖5 春季調查斷面兩端點處溫度、聲速剖面圖Fig.5 Temperature and sound speed profiles on two points of the investigation sections in spring

4月(春季)東海近海近表層海水水溫相對均勻，未達到溫躍層的標準。水聲調查春季某一東西向斷面內，水深從53 m向東約70 km增加至75 m，水溫總體垂直向較均勻，靠近東海沿岸處近海表水溫均勻，15～34 m深度，出現逆溫層，最大約為-0.6°C·m-1(圖 5(a));向東約 70 km 遠海處，逆溫層消失，表層55 m以內海水混合均勻，近底層溫度略有下降，未達到正溫躍層的標準(圖5(c))。9月(夏季)躍層顯著增強，不難看出沿聲學走航斷面的溫躍層的近遠海躍層上界深度都約為32 m左右，遠海躍層厚度較大，最大強度較小。近海躍層最大強度可達 0.11°C·m-1，分布在 32.5～40.5 m 左右(如圖6(a));遠海最大強度出現在61 m左右深度處，約為 0.86°C·m-1，躍層分布在 32.5～64.5 m(如圖6(c))。同時，此處計算聲速剖面是為下文利用UMPE模型仿真做準備。

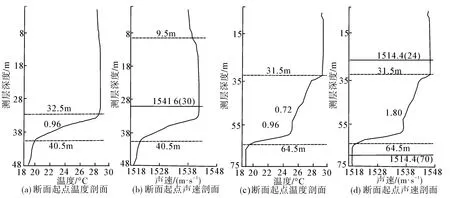
圖6 夏季調查斷面兩端點處溫度、聲速剖面圖Fig.6 Temperature and sound speed profiles on two points of the investigation sections in summer

3.3 實測數據分析溫躍層對水聲場影響

選取2008年04月和2009年09月對應上文溫躍層分析斷面處聲學傳播損失數據，2次調查時對應的海表氣象水文情況有所差異:08年側線附近伴隨偏北風 5～6 級，浪高 2.5～3.5 m，陰有陣雨;09 年調查期間天氣晴轉多云，東北風5～6級，浪高2～3 m。同時2個航次的水聽器陣分布水層存在微小差異，下文分析中選取水聽器深度對應較好的數據進行討論。

春季拖曳聲源深度約為40 m，夏季在33 m左右，隨著船體拖動深度變化在2 m以內，分別位于逆溫躍層(春季)、正溫躍層(夏季)當中。同時由于調查原因，同一測線獲取的數據的距離長度不一。從圖7不難發現，溫躍層對水聲傳播損失存在巨大的影響，夏季的傳播損失明顯大于春季，當水聽器從海表向下靠近溫躍層上界時，躍層中傳播損失逐漸增大。春季調查斷面起點存在較強逆溫躍層，對應夏季的強正溫躍層，傳播損失在靠近測量斷面起點(近聲源區域)兩者差別不明顯，距聲源距離超過5 km，傳播損失差別迅速增大。距聲源11 km處差值達到最大，在5.5 m左右深度層，最大相差約12～14 dB(圖7(a));在28 m左右深度層(圖7(b))，最大相差約16～18 dB，這證明了在溫躍層之上水層由上至下，躍層左右變大。隨著遠離聲源，靠近測線斷面的末端，逆溫躍層逐漸消失，水溫垂直分布均勻，春、夏之間的差別逐漸較小，直至維持在同一穩定水平。

同一溫躍層海洋環境中，頻率越高的聲波，傳播損失越大(如圖4)。春、夏季節海洋環境相差較大，躍層各異，溫躍層對不同頻率水聲場作用如圖8。

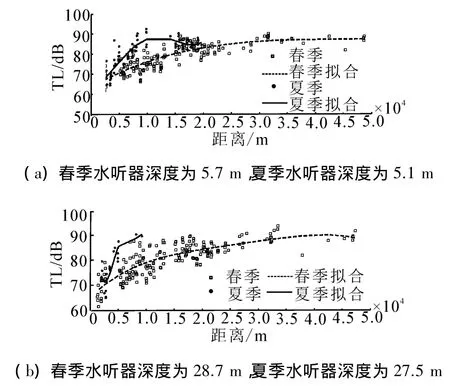
圖7 傳播損失季節對比，聲源頻率為0.58 kHzFig.7 Comparison of TL between different seasons，f=0.58 kHz

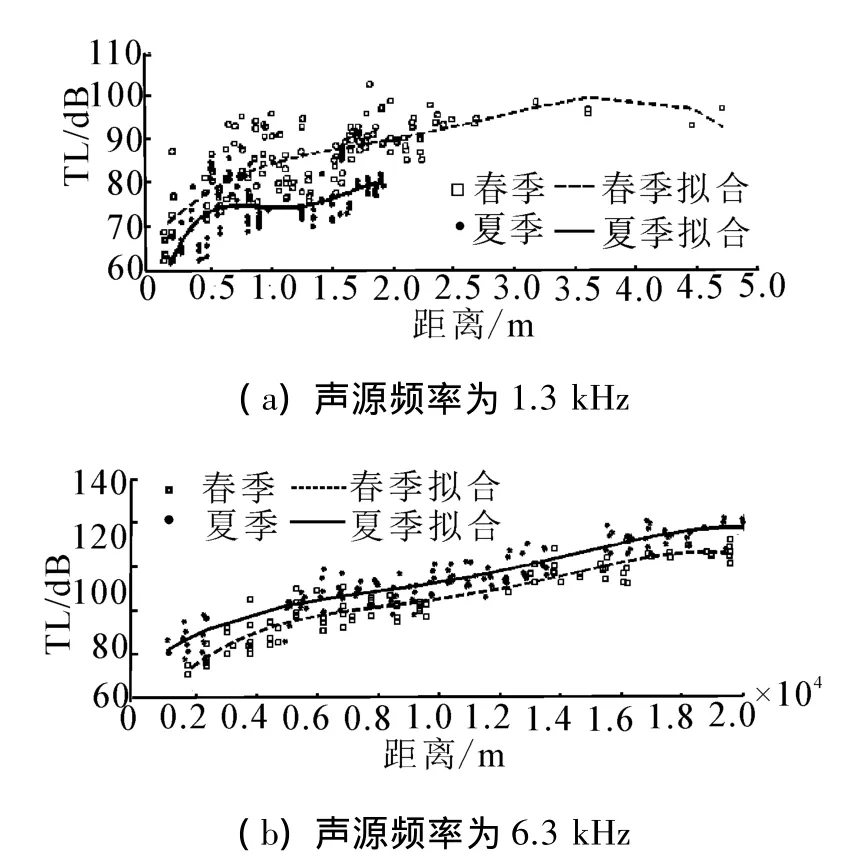
圖8 躍層對不同頻率水聲場影響對比圖，水聽器深度=5.7mFig.8 The influence of thermocline on acoustic TL of different frequency，hydrophone in the depth of 5.7m

不難發現，溫躍層對低頻水聲場影響較大，高頻較小。當聲源f=6.3 kHz，春夏季節的傳播損失曲線平整關系較好，相差6～8 dB(圖8(b));當聲源f=0.58 kHz 和 1.3 kHz，春夏傳播損失最大分別相差12～14 dB、9～11 dB，且隨距聲源的距離增大，變化幅度較大(圖8(a))。

春季(如圖9(a))逆溫躍層上界深度為17 m，水聽器位于22 m時傳播損失最大，5.7 m最小，10.3 m居中;說明逆溫層上界水層，隨深度的增大傳播損失逐漸增加。夏季(如圖9(b))正溫躍層上界深度在32 m左右，水聽器位于22.5 m時傳播損失最小，5.1 m 最大，10.2 m 居中;說明正溫躍層上界水層，隨深度的增大傳播損失逐漸減小。分析原因，聲傳播過程中聲線總是彎向聲速梯度減小的方向，正躍層上界隨深度增大溫度逐漸減小，這就導致了正溫度梯度海洋環境中，聲波逐漸向聲速減小的方向會集，亦即向溫度減小和深水區方向聚集，水深越小，傳播損失越大。逆溫躍層上界海洋環境相反，聲波向淺海會集，水深越小，傳播損失越小。

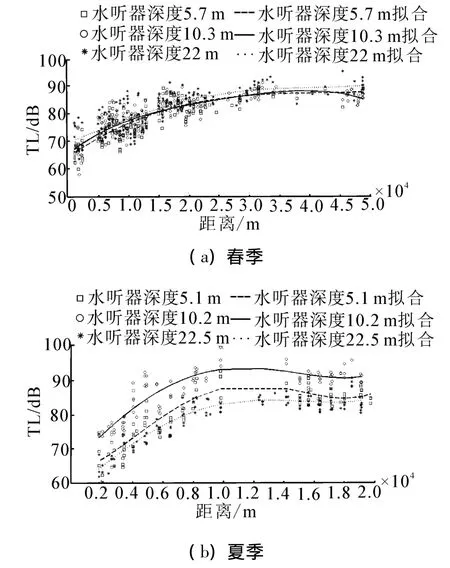
圖9 春、夏季節溫躍層上界傳播損失對比Fig.9 TL comparison in the water layer above thermocline in spring and summer

部分淺海溫躍層下界直達海底，獲取實測數據的水聽器陣位于溫躍層上界或者處于溫躍層中，未達到躍層下界水層，因此本文實測數據重點分析躍層上界水層，下文利用UMPE補充模擬分析躍層下界水層的傳播損失。

4 UMPE模型補充分析

李家訊(2009)[19]利用Kraken簡正波模型對不同聲速剖面下聲傳播損失場進行了模擬實驗，淺海聲速剖面主要是受溫度剖面影響，不同聲速剖面反應了不同的溫度剖面，即不同性質的溫躍層特征。但是該文章沒有具體提出是溫躍層的影響，本文利用實測數據對該模式在中國近海的適應性進行驗證，再利用UMPE拋物模型重點研究溫躍層以下水層聲傳播損失分布。

上文分析聲學調查斷面海底、海表與聲學相關信息如圖10所示。春、夏2個航次海表浪高相當，僅存在風向和天氣特征的差異，這對聲學調查結果影響較小。水深變化較小，海底地形相對平坦，最深75 m，最淺在53 m。在長約70 km斷面上，由淺至深分布有粉砂質粘土、粘土質砂和砂(沒有再細分)。UMPE模型的不足之一在于無法對海面海表的分布特征進行區域細分，只能做單一處理。根據實際海況將聲學參數融入UMPE模型，進行仿真模擬，春、夏季的聲速剖面如圖5(b)、圖5(d)、圖6(b)、圖6(d)所示，由于高頻聲源聲波傳播較短，模擬聲源頻率定為300 Hz。

從圖11不難發現，春季傳播損失場整體低于夏季。夏季正溫躍層條件下，聲速相對較大，聲能衰減迅速，且從表層向下，傳播損失逐漸減小，這與前文分析的在躍層上界水層，從表層向下傳播損失逐漸減小相對應，隨著傳播距離的增加，聲能逐漸向海底聚集。由于UMPE模型模擬的是窄角聲源，難以達到實測調查使用的近似無指向性聲源效果。但對比圖11(a)、圖11(b)易得到負溫躍層海洋環境中聲信道效果較好，聲波傳播距離更大，同時聲波向中上層海水折射。

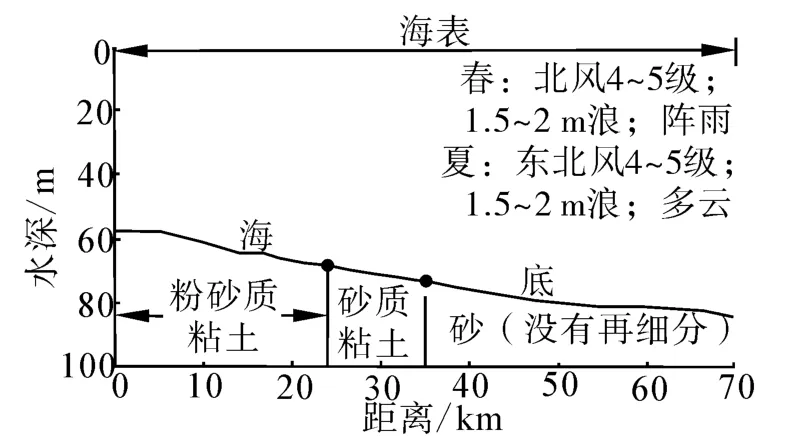
圖10 聲學調查斷面海底、海表聲學參數分布圖Fig.10 Acoustic parameters in sea bottom and surface of acoustic

UMPE模型在模擬高頻、無指向聲源存在不足，采用降頻、窄角聲源處理，能夠滿足分析溫躍層對水聲場的影響的要求。提取春、夏季46、61、71 m 3個位于溫躍層下界的水層傳播損失進行對比，近場傳播損失相差甚小;春季逆溫躍層海洋環境中，71 m水層傳播損失最大，46 m水層傳播損失最小，說明逆溫躍層下界水層聲能傳播損失隨深度增大逐漸增大(圖12(a));夏季正溫躍層海洋環境中，近場傳播損失變化復雜，這主要是受窄角模型的影響，結合圖11(b)和圖12(b)不難發現，遠場71 m水層傳播損失最小，46 m最大，61 m居中，這說明正溫躍層下界水層聲能傳播損失隨深度增大而增大減小。

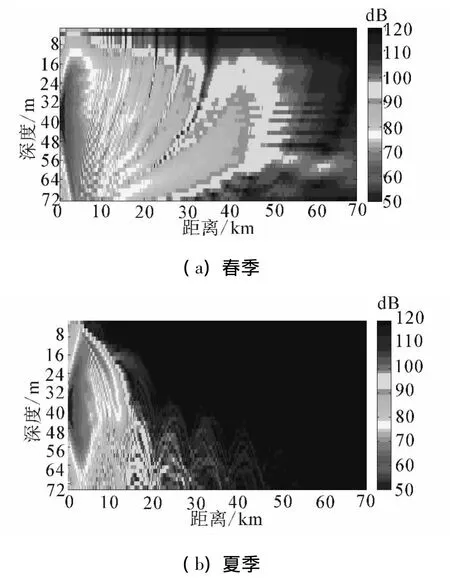
圖11 春、夏傳播損失場對比圖Fig.11 The comparison of transmission loss between spring and summer

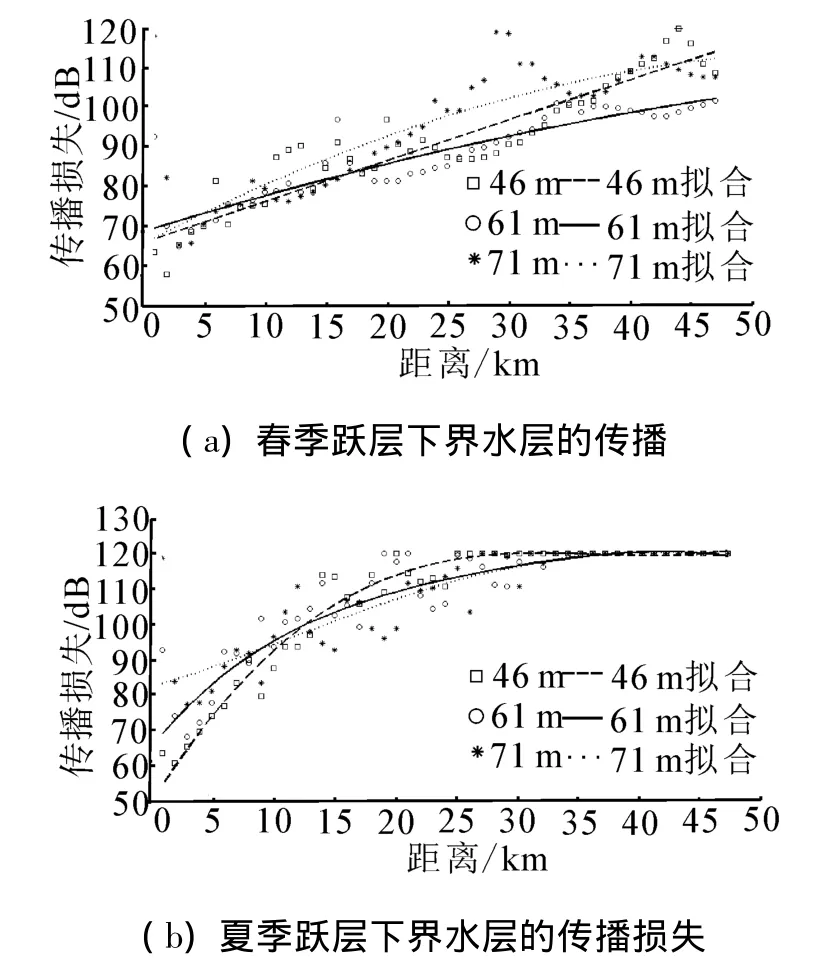
圖12 春、夏溫躍層下界水層傳播損失對比Fig.12 Different layers of transmission loss in spring and summer below the thermocline

5 結論

溫躍層是水聲傳播損失垂向變化劇烈的水層，正、逆溫躍層上、下層都伴隨有不同的變化趨勢，靠近溫躍層所在的深度傳播損失變化較快。同時，溫躍層對不同頻率水聲場作用各異，本文綜合利用聲學調查資料和聲學模型分析近海溫躍層對水聲場的影響，對聲學研究和聲學調查提供了一定的理論依據，得出如下結論:

1)無躍層或溫度垂直梯度較小時，對水聲場影響不大。溫躍層上界水層，逆溫躍層環境中聲傳播損失隨深度增大而逐漸增大;正溫躍層環境中，聲傳播損失隨深度增大而逐漸變小;變化速度向靠近躍層深度而加大。

2)溫躍層對不同頻率水聲場環境影響各異，聲源頻率越高，影響越小，隨與聲源距離的加大，傳播損失曲線平整關系較好，6.3 kHz聲源在5.7 m深度春、夏差別在6～8 dB;聲源頻率低，影響越大，傳播損失曲線差異隨距離振幅波動較大，0.58 kHz聲源在5.7 m深度春、夏季最大差別可達12～14 dB。

3)實測數據驗證UMPE聲學模型在高頻、窄角聲源方面的不足，但基本能夠滿足對溫躍層對水聲場影響的研究需要。并仿真溫躍層下界水聲場的影響，發現躍層下界水層隨深度增大，變化趨勢與對應躍層環境躍層上界水聲場變化趨勢一致。

由于實測數據分布層次的原因，同時受到部分研究淺海區域溫躍層直達海底的限制，重點分析的是溫躍層上界水聲傳播損失，并且采用UMPE二維聲學模型補充分析溫躍層下界溫度均勻的水層。以后將進一步研究淺海溫躍層對水聲場的作用，同時也將研究深海溫躍層對水聲場的影響。

[1]URICK R J.Principles of underwater sound[M].3rd ed.Los Altos:Peninsula Pub，1983:1-2.

[2]PFLUG H W.UWB pulse shaping for IEEE 802.15a[C]//Proceedings of the 38th European Microwave Conference.London ，UK，2008:713-716.

[3]張中兆，沙學軍，張欽宇，等.超寬帶通訊系統[M].北京:電子工業出版社，2012:15-17.

[4]ARSLAN H，CHEN Z N，BENEDETTO M D.Ultra wideband wireless communication[M].New York:A John Wiley＆ Sons，Inc，2006:189-193.

[5]侍茂崇.物理海洋學[M].濟南:山東教育出版社，2004:49-61，73-74.

[6]EIRINI K，GOTINI N P.An overview of the IEEE 802.15.4a standard[J].IEEE Communications Magazine，2010，48(1):47-53.

[7]BAO Qinghua，HUI Shaohua，WANG Huizhao.An experiment study of acoustic scattering from thermocline in shallow sea[J].Chinese Journal of Acoustic，1994，13(1):22-30.

[8]SIDERIUS M，PORTER M B，HURSKT P，et al.Effects of ocean thermocline variability on nonecoherent underwater acoustic communications[J].J Acoust Soc Am，2007，12(4):1895-1908.

[9]ZHANG Lin，DA Lianglong，XU Guojun.Simulation research on the effect of thermocline on underwater sound propagation[J].System Simulation and Scientific Computing，2012，121(4):52-60.

[10]張旭，張永剛.淺海溫躍層對聲信道影響的仿真研究[J].系統仿真學報，2012，24(10):2167-2171.ZHANG Xu，ZHANG Yonggang.Simulation for acoustic channel influenced by shallow-water thermocline[J].Journal of System Simulation，2012，24(10):2167-2171.

[11]PETER F W，REX K A，ARTHUR B B.The North Pacific Acoustic Laboratory deep-water acoustic propagation experiments in the Philippine Sea[J].J Acoust Soc Am，2012，131(1):1-11.

[12]SMITH K B，TAPPERT F D.The University of Miami parabolic equation model[EB/OL].Miami:the University of Miam，1993，(2000-09-16)[2014-04-01].http://oalib.hlsresearch.com/.

[13]TAPPERT F D.Parabolic equation method in underwater acoustics[J].J Acoust Soc Am，1974，55(Suppl):34.

[14]KELLER J B，PAPADAKIS J S.Wave propagation and underwater acoustics[M].New York:Springer-Verlag，1977:224-287.

[15]楊士莪.水聲傳播原理[M].哈爾濱:哈爾濱工程大學出版社，1994:66-69.

[16]國家技術監督局.中華人民共和國國家標準 GB12763.海洋調查規范-海洋調查數據處理[S].北京:中國標準出版社，1992:67-70.

[17]鄒娥梅，熊學軍，郭炳火，等.黃、東海溫鹽躍層的分布特征及其季節變化特征[J].黃渤海海洋，2001，19(3):8-18.ZOU Emei，XIONG Xuejun，GUO Binghuo，et al.Characteristics and seasonal variations of the thermocline and halocline in the Huanghai Sea and the East China Sea[J].Journal of Oceanography of Huanghai＆ Bohai Seas，2001，19(3):8-18.

[18]L-3 Communications SeaBeam Instruments.Multibeam sonar theory of operation[R].Walpole:L-3 Communications SeaBeam Instruments，1997.

[19]李家訊，張韌，王彥磊，等.Kraken海洋聲學模型及其聲傳播與衰減數值試驗[J].海洋科學進展，2009，27(1):51-58.LI Jiaxun，ZHANG Ren，WANG Yanlei，et al.Kraken marine acoustic model and its numerical experiment for acoutic propagation and decay[J].Advances in Marine Science，2009，27(1):51-58.