Mindlin矩形板在任意彈性邊界條件下的振動特性分析
薛開,王久法,李秋紅,王威遠,王平
(哈爾濱工程大學機電工程學院,黑龍江哈爾濱150001)
板結構作為工程中最為常見的一種基本單元構件,廣泛應用于航空航天、土木工程、車輛工程等諸多領域。由于共振問題,板的振動分析尤其是固有頻率的求解越來越引起人們的高度重視。因此,許多學者對板的振動特性進行了大量的研究,并取得了豐碩的成果。可是現有這些的研究中,很多是基于Kirchhoff薄板理論,此理論忽略了板的橫向剪切變形和轉動慣量的影響,因而會產生一定的誤差。當板較薄時,這種誤差可以忽略;當板的厚度增加到與板邊長相比不再是小量時,這種誤差就不能忽略了。
因此,近年來一些學者開始研究更符合真實情況的Mindlin板理論。目前常見的研究方法主要有能量法[1-4]和一些數值方法,如離散奇異卷積法[5-7]、微分求積法[8]等。但能量法需要選取合適的撓度函數,而撓度函數和邊界條件有關,其選擇比較困難;微分求積法的加權系數和樣點的選擇規則還不明確,離散奇異卷積法不能求解自由邊界問題,而且核序列的選取也無明確規則遵循;也有一些學者采用解析法進行了研究,如文獻[9-10]采用級數法分析了Mindlin板的振動問題,但種種方法只適用于至少有一對邊簡支的板;Gorman等[11-12]采用疊加法分析了Mindlin板在各種邊界條件下的振動,但此種方法求解過程過于復雜。
近年來,Li[13-14]提出了一種新的解析方法,即改進的傅里葉級數方法進行了任意邊界條件下薄板的振動分析。其通過將薄板結構的位移函數表示為傅里葉余弦級數和輔助多項式或者輔助級數的線性組合,使得彈性約束邊界條件能夠得到精確滿足,從而擴展了級數法的使用范圍,使其能應用到任意的邊界條件下。
本文利用Mindlin板理論,采用改進傅里葉級數,將矩形板的位移函數及2個轉角函數表達為標準的二維傅里葉余弦級數和4項輔助級數的線性組合。利用Hamilton原理建立求解方程,建立線性方程組,得到一個標準的矩陣方程,然后求解矩陣的特征值得到Mindlin矩形板的固有頻率。最后,通過和已有文獻中的計算結果進行對比來驗證本方法的正確性。
1 理論模型的建立
本文所研究的Mindlin矩形板模型如圖1所示。板結構的4個邊界處分別設置橫向位移彈簧、旋轉約束彈簧和扭轉約束彈簧3種類型的彈簧,通過改變剛度值來對任意邊界條件進行模擬。所有的經典邊界條件都能夠通過將3種彈簧系數設置為無窮大或零來獲得。例如將四邊的橫向位移約束彈簧和扭轉約束彈簧的剛度值設置為無窮大,而將四邊的旋轉約束彈簧剛度值設置為零,就相當于模擬了四邊簡支的邊界條件。

圖1 任意彈性邊界條件下矩形板結構Fig.1 The rectangular plate with arbitrary elastic boundary condition
根據Mindlin板理論,矩形板自由振動的控制方程為

式中:w為撓度,ψx為x方向的轉角,ψy為y方向的轉角,ρ為密度,μ為泊松比,h為厚度,D=Eh3/(12(1-μ2))為彎曲剛度,k為剪切系數,剪切剛度G=E/[2(1+μ)]。
板結構的Hamilton方程為

式中:V為板結構的總勢能,T為板結構的總動能。對圖1所示的板結構,總勢能可寫為

式中:V1為矩形板的勢能,V2為模擬邊界條件的彈簧的勢能。
V1、V2和 T的形式分別為

2 Mindlin矩形板的位移函數
Mindlin矩形板的位移函數和2個轉角函數可通過沿x和y軸方向的2個分量來描述,本文中采用改進的二維傅里葉余弦級數展開來表示:

與x相關的輔助函數表示為

從式(12)和(13)可以很容易得到關系式ξ1a(0)= ξ1a(0)= ξ'1a(a)=0,ξ'1a(0)=1,以及 ξ2a(0)=ξ2a(0)= ξ'2a(0)=0,ξ'2a(a)=1。需要說明的是,此關系式并不是必需的,本文選擇滿足此關系式的輔助函數是為了后續數學推導的方便性與簡潔性。
與y相關的輔助函數可以將式(12)~(13)中的a和x分別用b和y進行替換得到。從方程(9)~(11)可以看出,位移函數和轉角函數展開時除了標準的二維傅里葉級數,還有4項輔助的單傅里葉級數。在四條邊界上,撓度和轉角關于x和y的一階偏導潛在的不連續將有效地轉移到了輔助項,因此,位移函數和轉角函數在整個板的求解域內展開時都有連續的一階導數。所以這種傅里葉級數解形式,不僅適用于任意邊界條件,也可以改善級數的收斂性。
將式(6)~(11)代入Hamilton方程(4)中有:

式中,A為未知的系數向量,其形式為

K為剛度矩陣,M為質量矩陣,其形式為
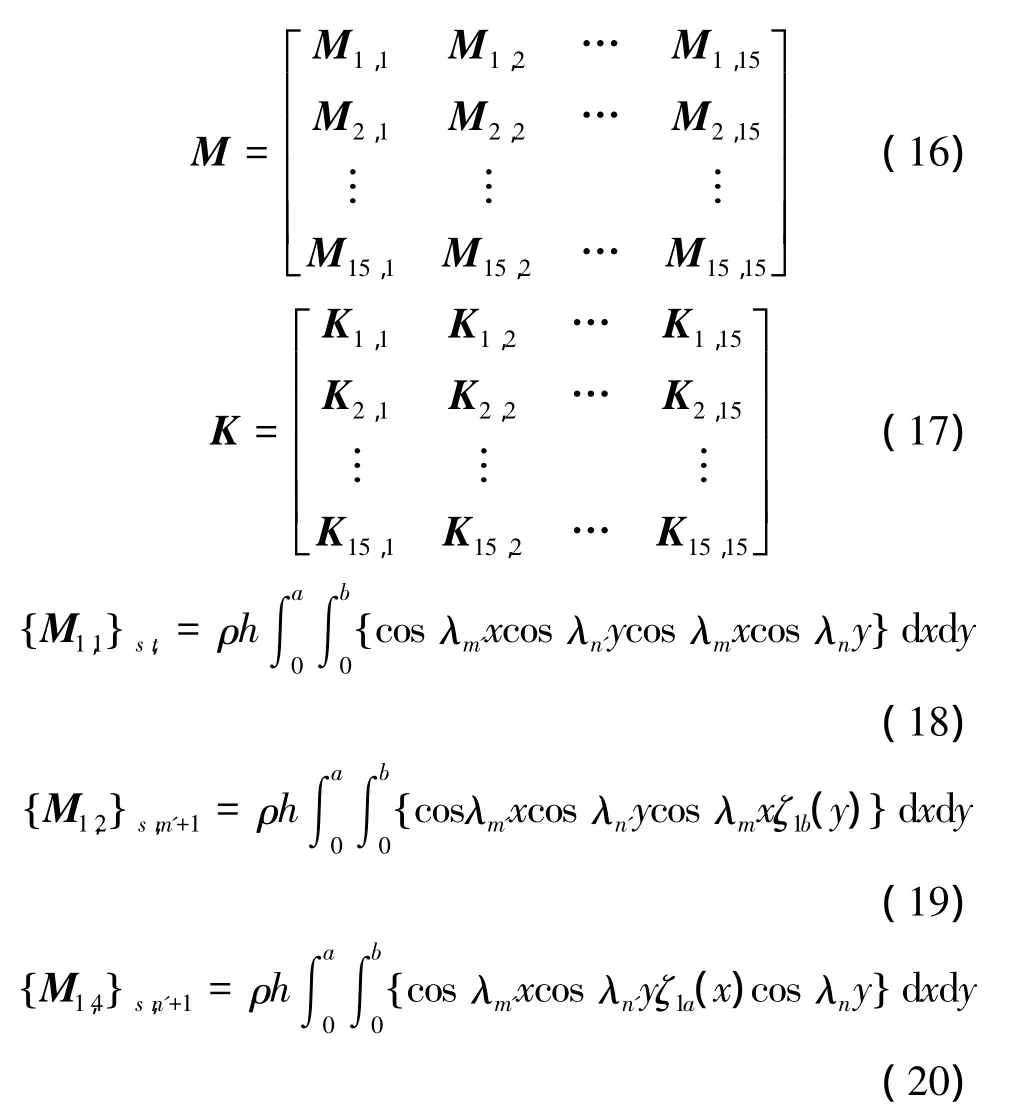
子矩陣 M1,3和 M1,5可以通過將 M1,2和 M1,4中的函數ζ的下標1更換為2得到。子矩陣M1,6到M1,15均為零矩陣。質量矩陣中的其他子矩陣和剛度矩陣可依此形式寫出。式中m'=0,1,…,M,m=0,1,…,M,n'=0,1,…,N,n=0,1,…,N,s=m(N+1)+n+1,t=m'(N+1)+1,M、N 表示展開級數的截斷值,這個根據結果所要的精度來確定。
求解式(14)中矩陣特征值,即可得到固有頻率和特征向量。每階特征向量實際上包含著所對應結構模態形狀分布的傅里葉系數。板的振動模態可以利用式(9)~(11)得到。
3 數值計算及分析
矩形板的結構及其材料參數為:板的長為a,寬為b,板的厚度為h,長寬比a/b,厚度比h/b,板的密度為 ρ=7 800 kg/m3,彈性模量 E=210 GPa,泊松比μ=0.3,剪切系數k=5/6。為了表述方便,本文中用C表示固支邊界條件,F表示自由邊界條件,SS表示簡支邊界條件。
為了檢驗本文方法的收斂性,表1給出了矩形板在 SS-F-SS-F 邊界條件下、長寬比為 0.5,厚度為 0.1時,截斷數M=N取不同值時的計算結果。簡支邊位移約束彈簧剛度和扭轉約束彈簧都設置為無窮大(本文中無窮大取值為D×107,而旋轉約束彈簧剛度都設置為零,自由邊上的3種類型的彈簧的剛度值都設置為零。從表1中可以看出,截斷數取較小值時就能得到精確的結果,而且隨著截斷數的增加,結果得到一致性改善者,即本方法有良好的數值穩定性。
為了驗證本文方法的準確性,考慮SS-F-SS-F邊界條件下板的振動情況。表2給出了不同厚度比和長寬比下Mindlin矩形板的前6階無量綱固有頻率,同時給出了文獻[9]中采用解析法求得的結果。可以發現本方法的結果和精確值的結果吻合良好,兩者的誤差在5‰內。在本文計算過程中,2個方向的位移展開采用相同的截斷數,表1中的值是M=N=12時的計算結果。

表1 SS-F-SS-F Mindlin矩形板頻率的收斂性Table 1 Convergence of frequency for SS-F-SS-F Mindlin rectangular plates
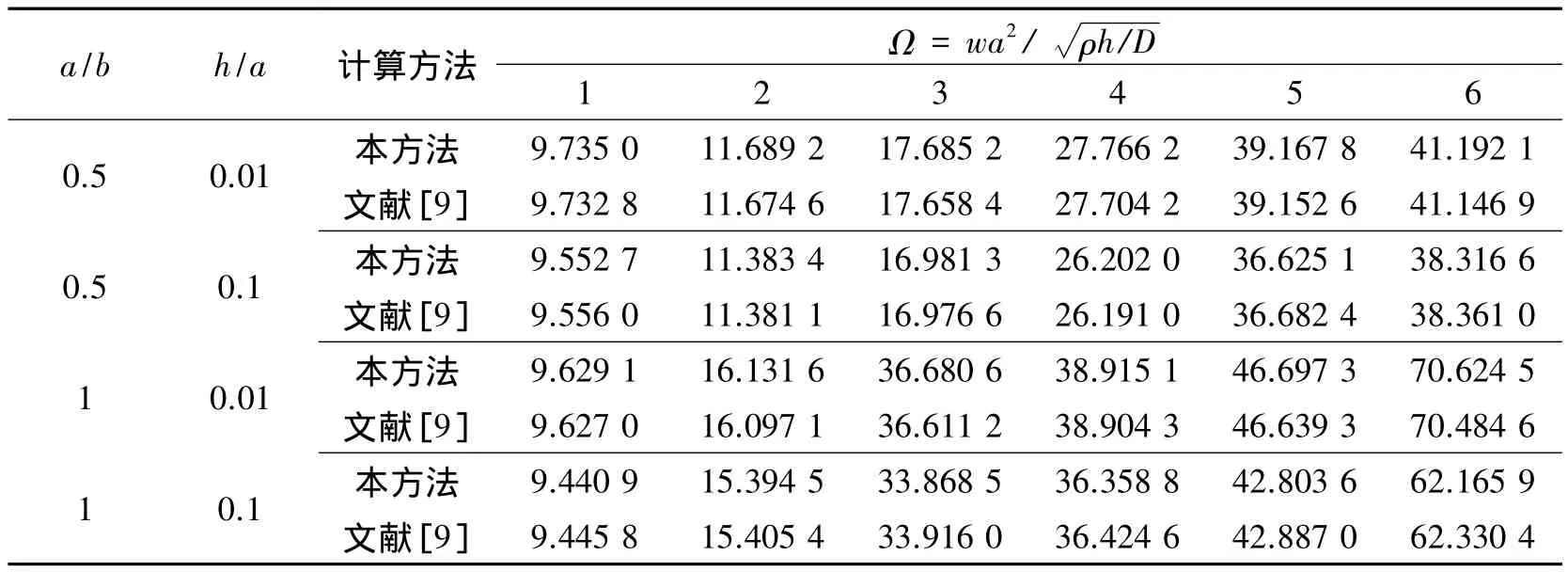
表2 SS-F-SS-F Mindlin矩形板的固有頻率Table 2 Natural frequency for SS-F-SS-F Mindlin rectangular plates
為了驗證本方法在處理其他經典邊界條件的準確性,表3給出了Mindlin矩形板在C-F-SS-F邊界條件下,長寬比為 0.4 和 1、厚度比為 0.1 和 0.2 時,4種情況下自由振動的無量綱頻率值,為了便于與文獻中的結果比較,表3中的無量綱頻率取為Ω=(ωa2/π2)(ρh/D)1/2。為了模擬固支邊,在 x=0 邊上的3種類型的彈簧都設置為無窮大,截斷數M和N取12。同時表中給出了文獻[1]用能量法和文獻[7]用離散奇異卷積法求得的結果,通過比較可以看出,本文的結果具有很高的精度。
本方不僅可以求解任意經典邊界條件下的振動問題,還可以求解任意彈性邊界條件下Mindlin板的振動問題。為了模擬任意邊界條件,在SS-F-SS-F板的基礎上,表4給出了厚度h=0.1時,x=0邊上的扭轉約束彈簧剛度Kyx0取不同值時,Mindlin矩形板的前6階無量綱固有頻率,從計算結果可知,隨著剛度的增加,同階的固有頻率也隨之增加。同時可以看出,當剛度值增加到D×107時,頻率值趨于穩定,其大小等于C-F-SS-F邊界條件下的頻率值,即邊界條件轉變了C-F-SS-F。

表3 C-F-SS-F Mindlin矩形板的固有頻率Table 3 Natural frequency for C-F-SS-F Mindlin rectangular plates

表4 x=0邊上不同扭轉剛度下SS-F-SS-F板的固有頻率,Kyx0=K×DTable 4 Natural frequency for SS-F-SS-F plates with torsional restraints at x=0,Kyx0=K×D
4 結束語
本文應用改進的傅里葉級數方法,將Mindlin矩形板的振動位移和2個轉角都表示為一個標準的二維傅里葉余弦級數和輔助級數的線性疊加,建立了任意彈性邊界條件下的自由振動模型。通過4項輔助級數的引入,使位移和轉角的導數在邊界處潛在的不連續得到了轉移,有效地克服了邊界不連續的問題,因此,本模型可以適用于任意的彈性邊界條件。本方法中,所有位移和轉角的展開系數可以通過Hamilton方程進行求解,而所有的固有頻率都可以通過求解矩陣特征值而得到。最后數值計算結果表明,本方法能夠快速收斂并具有很高的計算精度。
[1]LIEW K M,XIANG Y,KITIPORNCHAI S.Transverse vibration of thick rectangular plates-I.Comprehensive sets of boundary conditions[J].Computers & Structures,1993,19(1):1-29.
[2]LIEW K M,HUNG K C,LIM M K.Vibration of Mindlin plates using boundary characteristic orthogonal polynomials[J].Journal of Sound and Vibration,1995,182(1):77-90.
[3]XIANG Y,KITIPORNCHAI S,LIEW K M.Vibration analysis of rectangular Mindlin plates resting on elastic edge supports[J].Journal of Sound and Vibration,1997,204(1):1-16.
[4]ZHOU D.Vibrations of Mindlin rectangular plates with elastically restrained edges using static Timoshenko beam functions with the Rayleigh-Ritz method[J].International Journal of Solids and Structures,2001,38(32):5565-5580.
[5]MALEKZADEH P,SHAHPARI S A.Free vibration analysis of variable thickness thin and moderately thick plates with elastically restrained edges by DQM[J].Thin-Walled Structures,2005,43(7),1037-1050.
[6]HOU Y S,WEI G W,XIANG Y.DSC-Ritz method for the free vibration analysis of Mindlin plates[J].International Journal for Numerical Methods in Engineering,2005,62(2):262-288.
[7]XIANG Y,LAI K S,ZHOU L.DSC-element method for free vibration analysis of rectangular Mindlin plates[J].International Journal of Mechanical Sciences,2010,52(4):548-560.
[8]LIU F L,LIEW K M.Analysis of vibrating thick rectangular plates with mixed boundary constraints using differential quadrature element method[J].Journal of Sound and Vibration,1999,255(5):915-924.
[9]HASHEMI S H,ARSANJANI M.Exact characteristic equations for some of classical boundary conditions of vibrating moderately thick rectangular plates[J].International Journal of Solids and Structures,2005,42(3/4):819-853.
[10]HASHEMI S H,KHORSHIDI K,TAHER H R D.Exact acoustical analysis of vibrating rectangular plates with two opposite edges simply supported via Mindlin plate theory[J].Journal of Sound and Vibration,2009,322(4/5):883-900.
[11]GORMAN D J.Free vibration analysis of Mindlin plates with uniform elastic edge support by the superposition method[J].Journal of Sound and Vibration,1997,207(3):335-350.
[12]OHYA F,UEDA M,UCHIYAMA T,et al.Free vibration analysis by the superposition method of rectangular Mindlin plates with internal columns resting on uniform elastic edge supports[J].Journal of Sound and Vibration,2006,289(1/2):1-24.
[13]LI W L.Vibration analysis of rectangular plates with general elastic boundary supports[J].Journal of Sound and Vibration,2004,273(3):619-635.
[14]LI W L,ZHANG X F,DU J T,et al.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J].Journal of Sound and Vibration,2009,321(1/2):254-26.

