基于紅外雙光路的薄膜在線測厚系統(tǒng)的研究

曹智穎，趙 斌

基于紅外雙光路的薄膜在線測厚系統(tǒng)的研究

曹智穎，趙 斌*

（華中科技大學機械科學與工程學院儀器科學與技術系，武漢430074）

紅外測厚是薄膜在線測厚的主要方法之一，為了解決傳統(tǒng)的紅外測厚方法中尚存在的易受光源穩(wěn)定性的影響、不適用于高速薄膜生產線等缺點，采用雙光路參比測量的方法設計了一種雙光路紅外測厚系統(tǒng)，系統(tǒng)將光源的光分成測量路和參考路兩路，并使用單個CCD同時收集兩路光作為光強傳感器。描述了系統(tǒng)的成像原理，討論了系統(tǒng)對朗伯定律的適用性，最后通過對聚乙烯和聚四氟乙烯薄膜的標定實驗論證了系統(tǒng)的精度。結果表明，該方法精度高、魯棒性好，且能夠有效避免光源不穩(wěn)定帶來的影響。

測量與計量；薄膜測厚；紅外；雙光路

引 言

塑料薄膜種類繁多，廣泛地應用于日常生活和科學研究的各個領域，在塑料薄膜的生產線上，一般都會安裝在線測厚裝置來實時測量其厚度。目前，比較常用的塑料薄膜在線測厚技術有：射線測厚、紅外測厚、激光三角法測厚等。但是各類方法均有其自身的局限性，激光三角法測量透明材料效果不佳［1］；射線測厚包括X射線、γ射線和β射線測厚，應用最廣泛，但是存在放射性安全隱患、設備昂貴、能耗高；紅外測厚使用紅外光源，非放射性，對比其它在線測厚方法，有著明顯的優(yōu)勢。

傳統(tǒng)的紅外測厚方法尚存在一些缺點，使用單光路開環(huán)的紅外在線測厚系統(tǒng)，測量結果會受到光源穩(wěn)定性的影響；還有一些使用裝有兩片濾光片的調制盤產生兩束不同波長的單色光（分別作為測量光和參考光）的紅外在線測厚系統(tǒng)［2-3］，其不適用于高速的薄膜生產線，因為調制盤旋轉過程中，薄膜已經移動了一段距離，導致兩束光照射到薄膜的不同位置上，造成測量誤差。基于此，設計了一種紅外雙光路薄膜在線測厚系統(tǒng)，能夠有效解決上述問題。

1 工作原理

1.1紅外測厚基本原理

紅外透射測厚的基本原理是朗伯定律，即：

式中，I0為原始光強，α為吸收系數，t是光透射厚度。朗伯定律的本質來源于物質分子對于光的吸收。分子吸收紅外輻射后會引起構成分子中各化學鍵的振動，這些化學鍵的振動方式類似于雙原子振動。當入射光的頻率與分子中化學鍵的基頻、倍頻（約等于基頻的倍數）或組合頻率（多個基頻之和）相等的時候，就引起共振，該能量就會被分子吸收，其振幅將增強。這就表現為材料對特定波長的光能的強烈吸收。大部分紅外吸收是由X—H鍵（如O—H鍵、N—H鍵、C—H鍵）伸縮和彎曲振動的基頻的倍頻和組合頻產生的，這正是塑料薄膜對于紅外光吸收強烈的原因［4-5］。

1.2儀器光路結構及成像原理

儀器光路結構如圖1所示，儀器成像示意如圖2所示。光源使用大功率紅外發(fā)光二極管（light emitting diode，LED），波長850nm，光首先由準直透鏡準直，然后由分光棱鏡分為測量光路和參考光路兩路；在測量光路，光依次透過乳白散射玻璃、被測物和紅外帶通濾光片（直徑8mm，通帶中心波長850nm，半帶寬30nm），經反射鏡反射后透過分光鏡，最后透過成像透鏡打到CCD的光敏面上；在參考光路，光依次透過乳白散射玻璃、參考物和紅外帶通濾光片，經反射鏡反射后再經半透半反分光鏡反射，最后透過成像透鏡打到CCD的光敏面上。兩光路對稱布置，同名光學元件的參量一致。

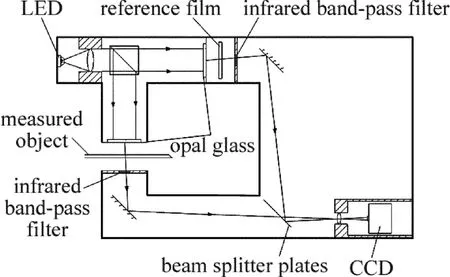
Fig.1 Optical structure of the system

測量時，被測物A通過測量路反射鏡所成像為A′，參考物B依次通過參考光路反射鏡和半透半反分光鏡成像為B″，由于光路對稱，此時A′和B″重合；半透半反分光鏡在45°的初始角度下逆時針旋轉一個微小角度以使A′和B″上下分開，最后通過成像透鏡把A′和B″成像到CCD光敏面上，CCD再將圖像傳送到計算機。

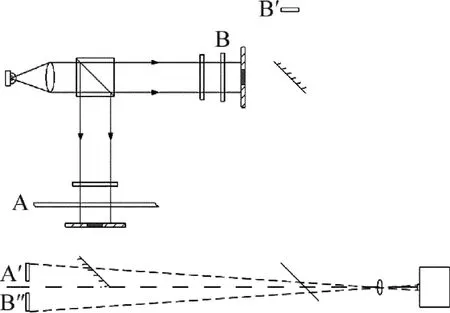
Fig.2 Schematic diagram of optical image system

使用CCD作為光強傳感器測量厚度，即以CCD采集到的圖像灰度值表征光強大小，此方法并不罕見，已有諸多先例，例如測量聚對苯二甲酸類塑料（polyethylene terephthalate，PET）薄膜局部厚度分布［6］、測量菲涅耳棱鏡局部厚度分布［7］以及紙張勻度［8］等等。

將系統(tǒng)光路簡化等效為如圖3所示，像A′和像B″相對于光軸上下對稱布置，分別通過透鏡成像到CCD光敏面的下部和上部。假設A′和B″都是理想的漫射體，其輻射亮度分別為LA和LB，根據經典的成像系統(tǒng)像面的照度公式，取A′上的一面微元dA，成像后對應的像面上的光照度為［9-10］：

式中，n和n′分為物方和像方的折射率，τA是光學系統(tǒng)的光透射比，U′是像方孔徑角，ω′是微元的像點主光線與光軸之間的夾角；f（ω′）即為修正函數，當軸外點的像方孔徑角很小時，f（ω′）＝cos4ω′。

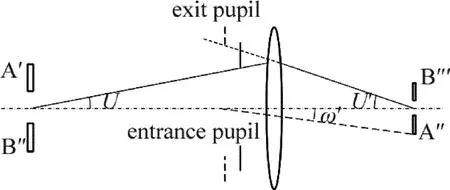
Fig.3 Schematic diagram of simplified equivalent optical image system

相機所采集到的輻射能是光敏面上接收到的光照度對時間（曝光時間）tint的積分，曝光時間很短，期間照度不變；假設相機響應輻射能到圖像灰度值的轉換效率為ρ，顯然ρ是相機增益G的函數，即ρ＝ρ（G）。綜上所述，CCD所獲得的圖像中光斑A″總的灰度值為：

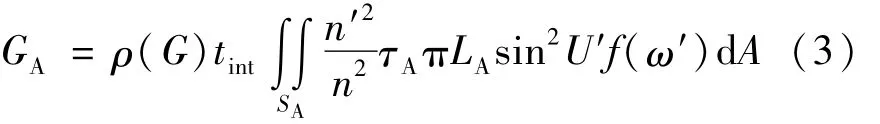
式中，SA是像A′的面積，同理光斑B?總的灰度值為：

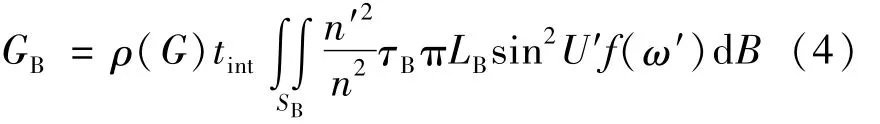
式中，SB是像B″的面積，dB是B″上的面微元，由此可得：

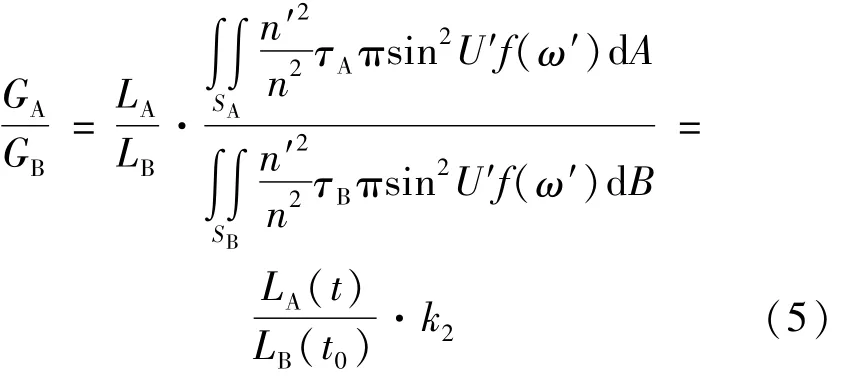
式中，k2為與光路結構相關的一常量，t和t0分別是A和B的厚度，如果LA（t）和LB（t0）依然滿足朗伯定律，則：

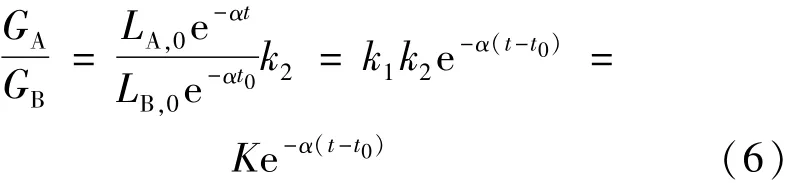
式中，LA，0和LB，0可以理解為膜厚度等于0時參考物和被測物的亮度，k1＝LA，0／LB，0，k1可以理解為薄膜之前經分光棱鏡分光后兩路光的光強比，K＝k1·k2，K為不放置薄膜時兩路光的灰度比。因此擬合標定K和α后，只要測得參考光路和測量光路的光斑的灰度GA和GB，就可以求出被測物的厚度t。

3 實驗數據分析

3.1擬合標定實驗

使用VC編寫程序實時采集相機圖像，如圖4所示；投影處理后由灰度的1階導數獲取兩個光斑的邊界，再通過排序統(tǒng)計獲取邊界內所有亮光斑的數量和灰度值總和，基于此就可以求得兩光斑的平均灰度值和兩光斑的灰度比值，圖像處理比較簡單不作贅述。

Fig.4 Light spot image collected in real-time

實驗樣品為厚度為15μm的聚乙烯（polyethylenex，PE）薄膜，擬采用多張薄膜疊合的方法來獲取不同厚度的被測物，首先來分析下簡單的疊加增厚帶來的影響。

在兩折射率不同的介面上，光會發(fā)生折射和反射，假設光在空氣與本實驗樣品聚乙烯的介面上（上下共兩個界面）的光強反射損失比為r；同理，當兩層聚乙烯薄膜疊合在一起的時候，層間有空氣，假設光透過一個空氣夾層光強透射比為τ；在參考路上放置厚度為t的薄膜，并將N張厚度為t的同一薄膜疊合起來作為被測物，顯然被測物中存在N－1個空氣夾層，則CCD采集到的兩路光的灰度值分別為：

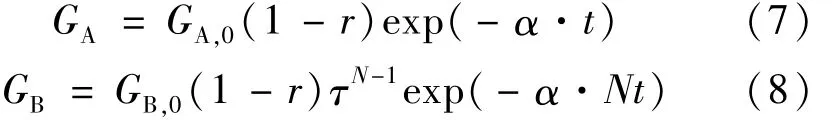
式中，GA，0和GB，0為不放置薄膜時兩路光的灰度，（7）式除以（8）式，并作化解：

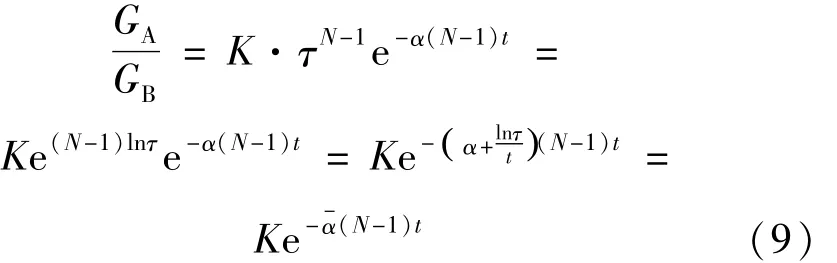
由上式可知，最終的灰度比仍然滿足朗伯定律，只不過由等效吸收系數α—＝α＋（lnτ）／t代替α。

在參考光路放置厚度為15μm的聚乙烯薄膜，在測量光路分別放置1層到9層的同一批聚乙烯薄膜，即厚度分別為15μm，30μm，45μm，60μm，75μm，90μm，105μm，120μm和135μm共9組，每組測量600次取平均，對這9組數據依照（6）式進行擬合，得到灰度比值（即相對透射比）和厚度的擬合標定曲線，如圖5所示。

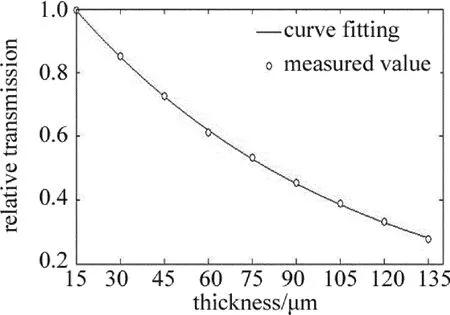
Fig.5 PE calibration curve

擬合結果K＝0.9962，α—＝－0.01053μm－1，即得標定公式：

再將測得的兩光斑灰度比代入標定公式，得到實測厚度值，如表1所示，最大誤差不超過1.5μm，且每組600個數據單次的測量重復性均小于0.5μm，精度和重復性均較高，這個結果還是比較保守的，因為薄膜很薄，操作中難免弄皺，直接疊合增厚本身亦不穩(wěn)定。由于標定得到的是被測物疊合時的等效吸收系數，故此數據只用以衡量儀器的精度，無法用來實測不同厚度的聚乙烯薄膜。

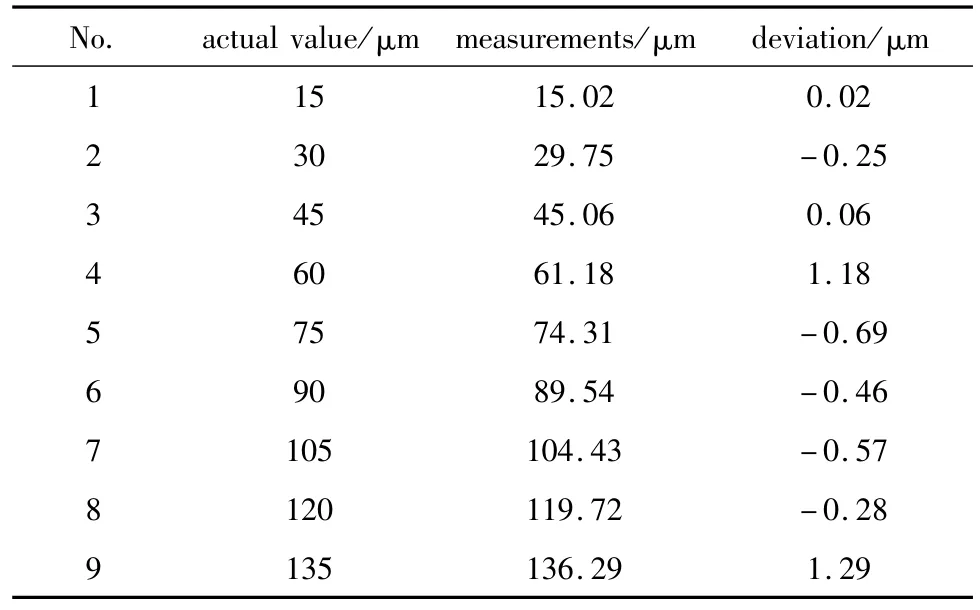
Table 1 PE calibration measurement data

仍使用疊合增厚的方法，為了準確地標定被測材料的吸收系數，可以使用與被測物折射率相近的液體或溶液填充層間間隙。聚四氟乙烯（polytetrafluoroethylene，PTFE）的折射率約為1.35，水的折射率為1.333，由菲涅耳定律可得水與聚四氟乙烯之間的界面上的反射率為：（1.35－1.333）2／（1.35＋1.333）2≈0.04‰，亦即使用水作為介質疊合聚四氟乙烯薄膜時，層間光強損失可以忽略不計。使用4張5絲10cm×2cm的聚四氟乙烯薄膜，其厚度分別為（使用螺旋測微器在其不同的區(qū)域測量10次取平均）：47.0μm，47.1μm，47.4μm，47.5μm，然后使用水作為介質疊合得到厚度：94.5μm，142μm，189μm，總共7組，參考路上不放置薄膜。由于薄膜本身厚度不均勻，故在每塊薄膜不同位置上隨機測量200次做中值濾波，標定擬合的數據如圖6和表2所示。

Fig.6 PTFE calibration curve

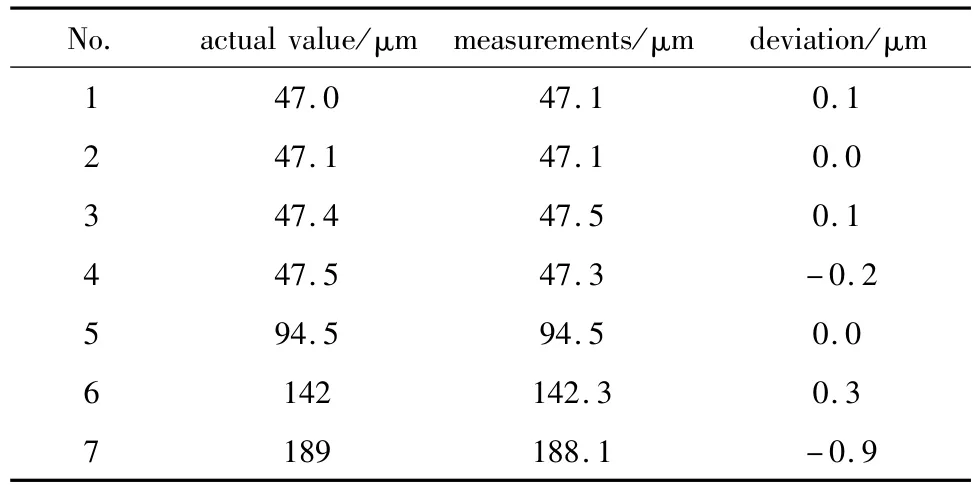
Table 2 PTFE calibration measurement data

擬合結果為K＝0.8914，α—＝－0.01244μm－1，相比聚乙烯實驗擬合出的參量K變小，主要原因是參考光路沒有放置薄膜，故薄膜與空氣界面的光透射比（1－r）亦蘊含在系數K中，其次兩次實驗的兩路光灰度比略有差異。

由表2可以看出，單層薄膜厚度的測量誤最大也僅為0.2μm，而多層薄膜的測量誤差較大，特別是4層疊合的時候誤差為0.9μm，主要原因分兩方面，首先薄膜疊合時難免混入氣泡、灰塵等一些雜質；其次由圖6可以看出，4層薄膜時由于厚度大，對應擬合曲線上該點的斜率小，也即微小的透射率差異就會導致較大的厚度測量誤差。

3.2光源光強變化對測量的影響

分別在參考光路和測量光路放置厚度為10絲（實測厚度100μm±5μm不均勻）的聚乙烯薄膜，通過降低LED的供電電壓來改變LED的亮度，獲取不同的光斑亮度下，兩光斑的亮度比值。實驗中使用的大功率紅外LED，采用650mA的恒流電源供電，工作電壓約為1.7V，恒流電源的輸入為直流12V。為了獲取較明顯的實驗現象，將直流穩(wěn)壓電源的輸出電壓調至6V以下，這時LED光強開始發(fā)生明顯的變化，并變得不穩(wěn)定。4次改變直流穩(wěn)壓電源的輸出電壓，每次測量100組數據，最終數據如圖7所示，縱坐標為灰度值和灰度比值，橫坐標為測量次數。對每組數據的光斑灰度和比值取均值如表3所示。

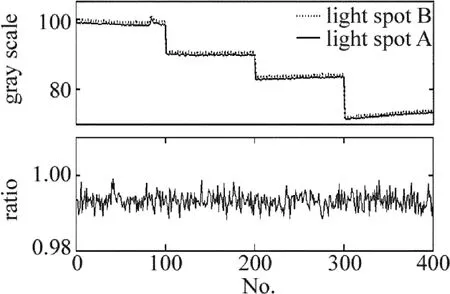
Fig.7 Curve of gray scale ratio with different light intensity

Table 3 Data of gray scale ratio with different light intensity

由表3可知，在光源光強變化導致光斑灰度從99變化到72的過程中，各組實驗的灰度比值之間的差異小于1‰，該值已經小于系統(tǒng)本身的單次測量的測量重復性，因此可以認為，光源光強的變化不會對該測量系統(tǒng)造成顯著影響。

4 結 論

針對傳統(tǒng)紅外薄膜測厚系統(tǒng)尚存在的一些局限，設計了一種雙光路紅外薄膜測厚方法，對系統(tǒng)的成像進行簡化和分析，推導出CCD收集到的兩路光的灰度比；為測試系統(tǒng)精度，設計了通過疊加薄膜來增厚的標定實驗，理論推導出兩路光的光強比仍然符合朗伯定律，實驗結果驗證了推導結論，由實驗數據可以看出，該系統(tǒng)的測量精度高，對聚乙烯薄膜15μm～135μm疊合增厚，測量誤差小于1.5μm，對50μm聚四氟乙烯單層測量誤差小于0.5μm，光源光強的變化不會對該測量系統(tǒng)造成顯著影響。

［1］ WANG Ch，ZHAO B.Research of thin plate thickness measurement based on single lens laser triangulation［J］.Laser Technology，2013，37（1）：6-10（in Chinese）.

［2］ ZHANG M H.Uses of the infrared technology for on-line gauging of plastic film thickness［J］.Journal of Zhejiang University of Technology，1985（2）：1-8（in Chinese）.

［3］ LIAO F Z，WEIH R，ZHAOW K，et al.A non-contact method for measuring the thickness of polyester film with infrared absorption［J］.Acta Metrologica Sinica，1990，11（4）：266-270（in Chinese）.

［4］ WORKMAN J，WEYER L.Practical guide to interpretive near-infrared spectroscopy［M］.2nd ed.Boca Raton，Florida，USA：Chemical Rubber Company Press，Inc.，2012：12-16.

［5］ MENG F F，WANG TW，ZHANG Q T.Preparation and performance analysis of near-infrared absorption PVB films［J］.Infrared and Laser Engineering，2012，41（11）：3003-3007（in Chinese）.

［6］ JOHNSON J，HARRIS T.Full-field optical thickness profilometry of semitransparent thin films with transmission densitometry［J］.Applied Optics，2010，49（15）：2920-2928.

［7］ MARTINEZ ANTON JC，GOMEZPEDRERO JA，ALONSO FERNANDEZ J，et al.Optical method for the surface topographic characterization of Fresnel lenses［J］.Proceedings of SPIE，2011，8169：816910.

［8］ CHENW，HU K T.Study on sheet formation with computer visual system［J］.World Pulp and Paper，2000，19（3）：48-50（in Chinese）.

［9］ QU E Sh，ZHANG H J，CAO JZh，et al.Discussion of illuminance formula in optical design［J］.Acta Optica Sinica，2008，28（7）：1364-1368（in Chinese）.

［10］ YU D Y，TAN H Y.Engineering optics［M］.Beijing：Press of Mechanical Industry，2011：82-83（in Chinese）.

Research of on-line film thickness measurement system based on infrared dual-light path

CAOZhiying，ZHAOBin
（Department of Instrument Science and Technology，College of Mechanical Science and Enginnering，Huazhong University of Science and Technology，Wuhan 430074，China）

Infrared thickness measurement is one of the main methods of online film thickness measurement，but traditional infrared thickness measurement method still has such defects that it is sensitive to the stability of light source and it is not applicable to high-speed film production line.In order to solve these problems，a dual-light path reference measurement method was used and a dual-light path infrared thickness measurement system was presented.In the system，the light source is divided into measurement light path and reference light path，using a single CCD connecting both the measurement light and the reference light as light intensity sensor.The imaging principle was described and the applicability of the system for Lambert law was discussed.Finally，calibration experiments for polyethylene and polytetrafluoroethylene film were conducted to demonstrate the accuracy.The experimental results show that the method has high precision and good robustness，and can effectively avoid the impact of the unstable of light source.

measurement and metrology；film thickness measurement；infrared；dual-light path

TN247；TH741

A

10.7510／jgjs.issn.1001-3806.2014.02.011

1001-3806（2014）02-0196-05

國家九七三重點基礎研究發(fā)展計劃資助項目（2013CB035405）

曹智穎（1989-），男，碩士研究生，主要從事紅外和激光精密測量方面的研究。

*通訊聯系人。E-mail：zhaobin63＠sohu.com

2013-05-10；

2013-06-13