基于全變差重構算法的數字全息研究

簡獻忠，周 海，喬靜遠，李 瑩，王 佳

基于全變差重構算法的數字全息研究

簡獻忠，周 海，喬靜遠，李 瑩，王 佳

（上海理工大學光電與計算機學院上海現代光學系統重點實驗室，上海200093）

為了消除傳統算法對數字全息重構過程中會出現0級像、共軛像干擾的問題，將壓縮感知理論與數字全息圖再現相結合，提出了基于全變差的兩步迭代收縮閾值重構算法（TwIST），并應用于數字全息圖壓縮感知全息圖重建。TwIST算法根據重構成分的特點增加正則約束，對相應的形態進行調整，在滿足全變差最小的特性的基礎上進行重構，提高了重構全息圖的質量。結果表明，TwIST算法可以對數字全息圖稀疏重建，利用35%的部分全息圖數據進行圖像重構，重構圖像峰值信噪比為36.46dB，且沒有0級像和共軛像等干擾。該研究結果對實現計算全息的實時性具有重要的意義。

全息；壓縮感知；計算全息；數字全息圖；全變差重構算法

引 言

數字全息是用CCD等光電探測器件代替全息記錄材料記錄全息圖，然后通過計算機用數字仿真的方法再現全息圖［1］。與傳統全息相比，這一方法制作成本低、成像速度快、具有明顯的簡易性和靈活性等特點［2-4］。經過多年的發展，出現了大量對數字全息重建的算法。傳統的數字全息重建算法［5-6］在重建過程中會出現0級像和共軛像等干擾的問題，而且重構過程都是對全息圖的全部數據進行的，因而存在較大的計算冗余［7］。

壓縮感知是近年來在信息處理領域中對傳統奈奎斯特抽樣理論的重要推廣和發展。它是CANDES，ROMBERG及華裔科學家TAO等學者在稀疏表示和優化理論的基礎上提出的信號重建理論［8-9］。直接將采樣與壓縮相結合，對稀疏或可壓縮的高維信號投影成的低維信號進行測量，然后通過最優化問題求解實現對原始高維信號的精確重構，這就是壓縮感知理論的本質。近年來，為了解決數字全息中重構圖像質量的問題，有研究者開始把壓縮感知理論應用到全息中。MARIM等人［10］將壓縮感知理論用于全息顯微鏡中，實現了在噪聲干擾下稀疏采樣重建微小物體的形狀。參考文獻［7］中說明了壓縮感知理論能夠很好地應用于數字全息，參考文獻［11］中采用正交匹配追蹤算法對全息圖進行重構，但是重構效果還待提高。

作者在分析了壓縮感知的原理和應用方法的基礎上，提出了基于全變差的兩步迭代收縮閾值重構算法，利用該算法對計算機模擬的數字全息圖的部分數據采樣進行重構，得到了較高質量的重構圖像，為實現全息實時顯示提供了一種新的技術途徑。

1 壓縮感知的基本理論

壓縮感知理論主要是從信號的稀疏表示、測量矩陣構造和算法重構這三部分來描述的。

1.1稀疏表示

考慮長度為n的離散信號x，可以用一組標準正交基Ψ1，Ψ2，…，Ψn線性表示，則該信號表示為：

顯然α是信號在Ψ域的表示，這里k＝1，2，…，n。

運用壓縮感知理論的關鍵問題取決于該信號是否具有稀疏性或者近似稀疏性，若（1）式Ψ中的α只有k個非零值（n?k），可認為信號是稀疏的。離散信號x能夠被精確重構的前提是系數向量α是系數的，即Ψ域是稀疏域，需要選擇合適的基來表示信號，才能使信號有足夠的系數以保證能夠精確重構。光滑信號的傅里葉系數、傅里葉小波系數等都具有足夠的稀疏性，均可以作為信號的稀疏基。

1.2測量過程

用一個與變換矩陣不相關的m×n（m?n）矩陣Φ對信號進行線性投影，可以得到線性測量值y：

測量值y是一個m×1矩陣，這樣使測量對象從n維降為m維。將（1）式帶入（2）式中，有：

式中，Φ為感知矩陣或測量矩陣。要保證可壓縮信號x從n維降到m維的過程中主要信息不丟失且能夠準確重建出原始信號，還要保證測量矩陣和稀疏基不相關性、測量次數m＝O［klg（n）］和測量矩陣滿足約束等距準則（restricted isometry property，RIP），O為計算復雜度的運算符。

1.3重構算法

目前，基于壓縮感知理論的重構算法主要包括最小l1范數法、匹配追蹤系列算法、迭代閾值法以及專門處理2維圖像問題的最小全變分等。這些算法都是基于兩種求解模型：l0求解模型和l1求解模型［12］，如下所示：

式中，‖α‖0為向量α的l0范數，表示α中非零元素的個數；‖α‖1為向量α的l1范數。

2 全變差的兩步迭代收縮閾值重構算法

［7］中分析了壓縮感知框架數字全息重構方法的可行性，采用全變差求整個空間內梯度l1范數，實現數字全息的重建。為了提高圖像的重構速度和質量，參考文獻［13］中提出了兩步迭代收縮閾值重構算法（two-step iterative shrinkage thresholding，TwIST）。在感知圖像重構中，為了提高重構圖像的質量，可以根據不同成分的特點增加正則約束，對相應的形態成分調整。除了稀疏表示的先驗條件以外，圖像平滑成分和邊緣輪廓成分通常還滿足全變差最小的特性，所以本文中在使用兩步迭代收縮閾值重構算法同時加入全變差最小正則項，進一步來改善重構成分的質量。

將（4）式轉化為凸規劃的l1范數求解，變形為帶有拉格朗日乘積的形式，求解目標函數取最小值的系數問題：

把全變差最小的約束加入重構算法中，（7）式變為：

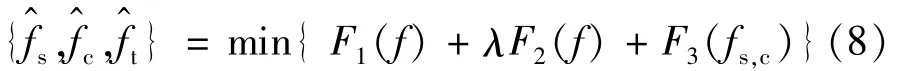
式中，F3（fs，c）＝∑k＝s，cV（fk），V（fk）表示全變差。

將V（fk）加入重構方程，基于全變差TwIST重構算法步驟如下所示，簡記：Tk，λ（x）＝Ψk｛Tλ［ΨkT（fk，j＋ΦTx）］｝，（k＝s，c，t），Tλ為閾值函數；Gk，h（x，y，u，p，q）＝（1－γ）x＋（γ－β）y＋βTk，λ×，其中γ和β為決定算法收斂速度的參量參量的設定為：步參量μ＝1；閾值步長h＝1；迭代終止值為ε。

（1）初始化，迭代次數為j＝0，重構圖像為f0＝fk，0＝fVs，0＝fVc，0＝0，最大迭代次數為jmax。

（2）更新第1次迭代數據：j＝j＋1。

（3）更新第j＋1次的迭代數據：

（4）對兩次目標函數值進行比較，若F（fj＋1）＞F（fj），則h＝2h，返回第（3）步，否則繼續下一步。

（5）判斷是否滿足終止條件，若j＋1＝jmax，則終止迭代，輸出重構圖像fj＋1，否則更新迭代次數j＋1，轉至第（3）步繼續執行。

3 實驗仿真與對比

3.1數字全息重構實驗

在實驗中，使用Mach-Zehder干涉儀實驗裝置獲取一幅“N”字母的全息圖，Mach-Zehder干涉儀實驗裝置如圖1所示。重構采用PC平臺，硬件為英特爾G630 2.70GHz、內存2G，軟件為Windows XP，MATLAB R2010a版本。圖2a是CCD拍攝的全息圖；圖2b是卷積算法重構的圖；圖2c是快速傅里葉逆變換重構的圖；圖2d是全變差TwIST算法重構的圖。

Fig.1 The Mach-Zehder interferometer experimental setup

Fig.2 Digital hologram and the reconstructed image

3.2數值模擬重構實驗

為了進一步說明該算法的特點，對標準測試圖進行數值模擬實驗。首先產生數字全息圖，模擬物光波振幅和數字全息圖均為256灰度級的256pixel× 256pixel圖像，如圖3a、圖3b所示；圖3c是卷積算法重建的圖像；圖3d為正交匹配追蹤（orthogonal matching pursuit，OMP）算法重構的圖像；圖3e是全變差TwIST算法重構的圖像。

Fig.3 The simulation of digital hologram and the reconstructed image

通過對圖2d和圖2b、圖2c進行對比，說明了壓縮感知對數字全息圖重構的可行性，而且壓縮感知算法重構的圖像明顯沒有0級像和共軛像，可重構出高質量的圖像，說明本文中提出的全變差TwIST算法能夠高質量地重構圖像。

通過對圖3d、圖3e和圖3c進行對比，說明了35%的數字全息圖壓縮感知重構的圖像質量明顯優于100%數字全息圖傳統算法重構圖像的質量，顯示了所有細節；對圖3d和圖3e進行對比，OMP算法重構圖像峰值信噪比（peak signal-to-noise ratio，PSNR）為26.16dB，而全變差TwIST算法重構圖像的PSNR值為36.46dB。

4 結 論

實驗結果表明，TwIST算法能夠應用在數字全息圖的重構，重構了高質量的再現像，PSNR值為36.46dB，消除了傳統重構圖像中出現的0級像和共軛像的問題，顯示了所有細節，峰值信噪比高。在全變差TwIST算法重構過程中，原始物體本身的透射重構是直接通過數字全息圖獲得的線性觀測向量和傳感矩陣得到的，同時使用最小全變差約束可以使得圖像在重構過程中更為稀疏，進而有助于消除圖像邊緣偽影對重構結果所帶來的干擾，因此獲得了高質量的重構圖像。

TwIST算法能夠應用在數字全息圖的重構，僅用35%的全息圖數據重構了高質量的再現像，這實現了全息圖數據的壓縮，減少了數據采集量和計算冗余，為計算全息實時顯示提供了一種新的技術途徑。

參考文獻

［1］ JIAN X Z，ZHANG H，FAN JP，et al.Research of computergenerated hologram based on FPGA technology［J］.Laser Technology，2011，36（1）：26-32（in Chinese）.

［2］ CHEN N.Research on digital holography［D］.Guangzhou：Jinan University，2004：58-80（in Chinese）.

［3］ FENG Y J，DING JP，ZHOU J.Self-focusingmatched filter produced by computer-generated hologram［J］.Optics Communications，2000，184（1）：89-93.

［4］ YU Z L，JING F.Computer generated hologram［M］.Beijing：Tsinghua University Press，1984：1-194（in Chinese）.

［5］ SONG X F，ZHAO BQ，QIN A.Comparison of three basic reconstruction algorithms in digital holography［C］／／Optical Test and Measurement Technology and Equipment.Chengdu：International Society for Optics and Photonics，2009：40-46.

［6］ LI JC.FFT computation of angular spectrum diffraction formula and its application in wavefront reconstruction of digital holography［J］.Acta Optica Sinica，2009，29（5）：1163-1167（in Chinese）.

［7］ WU Y C，WU X C，WANG Z H，et al.Reconstruction of digital inline hologram with compressed sensing［J］.Acta Photonica Sinica，2011，31（11）：1109001（in Chinese）.

［8］ CANDESE J，ROMBERG J，TAO T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489-509.

［9］ CANDESE J，TAO T.Near-optimal signal recovery from random projections：universal encoding strategies［J］.IEEE Transactions Information Theory，2006，52（12）：5406-5425.

［10］ MARIM M M，ATLAN M，ANGELINIE D，et al.Compressed sensing for digital holographic microscopy［C］／／Biomedical Imaging：From Nano to Macro，2010 IEEE International Symposium.Rotterdam，Holland：IEEE，2010：684-687.

［11］ MA JSh，XIA F P，SU P，et al.Study on compressive sensing phase-shifting digital holography［J］.Semiconductor Optoelectronics，2013，34（1）：130-133（in Chinese）.

［12］ CHEN SSh B，DONOHO D L，SAUNDERSM A.Atomic decomposition by basis pursuit［J］.SIAM Review，2001，43（1）：129-159.

［13］ BIOUCAS-DIAS JM，FIGUEIREDOM A T.A new TwIST：twostep iterative shrinkage／thresholding algorithms for image restoration［J］.IEEE Transactions on Image Processing，2007，16（12）：2992-3004.

Study on digital holography based on the total variation reconstruction algorithm

JIANXianzhong，ZHOUHai，QIAOJingyuan，LI Ying，WANGJia
（Shanghai Key Laboratory of Modern Optical System，Electrical Engineering College，University of Shanghai for Science and Technology，Shanghai200093，China）

In order to eliminate the zero-order image and the conjugate image interference problems in the traditional algorithm for reconstruction of digital hologram，a new algorithm based on the total variation of the two-step iterative shrinkage thresholding（TwIST）was proposed combining compressive sensing theory with reconstruction of the digital hologram.According to the characteristics of the reconstruction component，the TwIST algorithm based on the total variation improves the quality of the reconstruction of hologram.The simulation results show that the hologram can be reconstructed from a sparse hologram with TwIST reconstruction algorithm a high quality image was reconstructed from 35%of a hologram and the peak signal-to-noise ratio（PSNR）of the reconstructed image was36.46dB without zero-order image and conjugate image interference.The study is helpful for implementing real-time computer-generated hologram.

holography；compressive sensing；computer-generated hologram；digital hologram；total variation reconstruction algorithm

O438.1

A

10.7510／jgjs.issn.1001-3806.2014.02.019

1001-3806（2014）02-0236-04

上海市高等學校建設基金資助項目（2009014）；上海市研究生創新基金資助項目（JWCXSL1302）

簡獻忠（1969-），男，副教授，博士，主要從事數字全息、嵌入式技術應用等方面的教學與科研工作。

E-mail：jianxz＠usst.edu.cn

2013-04-23；

2013-06-03