永磁球形電機的支持向量機模型的參數尋優

鞠魯峰 王群京 李國麗 胡存剛 錢 喆

（1.合肥工業大學電氣與自動化工程學院 合肥 230009 2.安徽大學電氣工程與自動化學院 合肥 230601）

1 引言

可實現多自由度運動的球形電動機對機器人、機械手等做空間多維運動的精密裝置意義重大，它可以簡化系統的復雜程度，減小系統的體積，提高整個系統的動態性能、穩定性和定位精度。

球形電機本體的結構參數對球形電機磁場以及轉矩特性有著直接的影響，因此，對球形電機本體結構參數進行優化，是球形電機的研究過程中的一項重要內容。由于球形電機本身結構復雜，若采用傳統的有限元法建立數學模型，由于球形電機結構參數的優化計算中，需要進行非常多次迭代，因此，計算時間較長。所以，筆者提出利用支持向量機進行球形電機結構參數設計的方法。

支持向量機（Support Vector Machine，SVM） 是一種建立在統計學習理論基礎上的機器學習方法，根據結構風險最小化原則盡量提高分類器的泛化能力[1]，即在由有限的訓練樣本獲得小誤差的情況下，仍然能夠保證對獨立測試集的小誤差[2]。SVM在使用過程中一個突出問題是模型參數的選擇。對于不同的樣本空間數據，不同的參數選取，將會對最終的分類及回歸結果產生非常大的影響[3]。一般支持向量機的參數選擇都是憑借經驗法或實驗法，這樣不僅計算量大、效率低，而且選取的參數往往不是全局最優參數，限制了支持向量機的應用。為了克服這些缺陷，目前比較常用的 SVM 參數尋優方法包括：網格尋優算法[4]、基于遺傳算法（Genetic Algorithm，GA）的尋優算法[5]、基于粒子群算法（Particle Swarm Optimization，PSO）的尋優算法[6,7]等。

本文針對球形電機的結構參數與轉矩的樣本數據，分別利用網格尋優算法、GA尋優算法、PSO尋優算法來計算球形電機 SVM 模型的最優參數，分別比較三種算法得到的參數，從而獲得最佳方案。

2 球形電機有限元分析

在對永磁球形電機建立 SVM 模型之前，首先需要建立訓練集，即樣本空間。本文研究的球形電機的結構如圖1所示。轉子由平行于赤道面的4層圓柱形磁極組成，24個定子線圈等緯度間隔分布在赤道面兩側。轉子輸出軸末端用于電機三自由度轉矩的輸出。

圖1 永磁球形電機結構圖Fig.1 Model of the permanent magnet stepper motor

由于永磁球形電動機本體復雜的結構，以及定轉子磁極不對稱等，所以對球形電機整體轉矩的分析還缺少系統有效的分析方法。目前主要的方法是首先用積分方程法對電機氣隙磁場進行分析，在此基礎上利用麥克斯韋張量法對電磁轉矩進行計算[8]。因為永磁球形電動機轉子沒有導磁性能材料，所以整個電機的轉矩模型可用單個定轉子磁極對相互作用模型來疊加。圖2所示為單個定轉子磁極對模型示意圖。圖3為計算得到的單個定轉子磁極對的轉矩特性曲線。

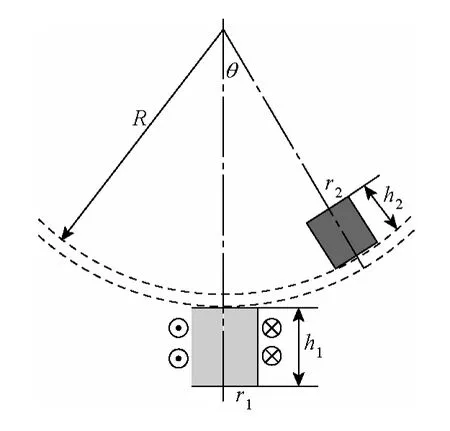
圖2 單個定轉子磁極對示意圖Fig.2 Schematic diagram of one pair of stator-rotor poles

圖3 單個定轉子磁極對轉矩特性曲線Fig.3 The torque characteristic curve of one pair of stator-rotor poles

永磁球形步進電機的主要結構參數包括：定轉子極之間的夾角（失調角）θ、轉子半徑R、轉子磁極半徑r、轉子磁極高h、電機氣隙g、線圈總安匝數NI、定子線圈長度 L、線圈孔徑d、線圈外徑D等。從圖3可知，轉矩隨失調角θ基本呈線性變化。所以，固定失調角θ=10°，分別以轉子磁極半徑r、轉子磁極高h、電機氣隙g、轉子半徑R、線圈總安匝數NI、定子線圈長度L、線圈孔徑d和線圈外徑D作為特征屬性，建立樣本空間。表1所示為特征屬性的取值分布。理論上，一共可以獲得48個樣本數據。根據正交實驗設計方法[9]，選取 150個樣本數據。其中，100個用來作為訓練集，50個作為測試集。

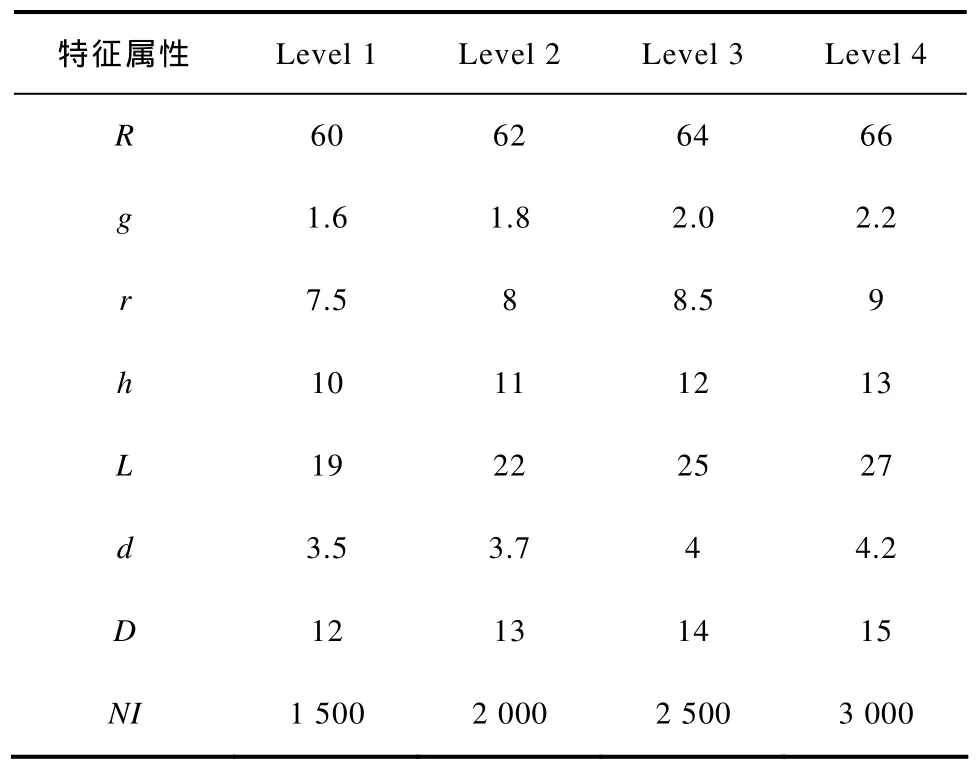
表1 樣本空間數據分布Tab.1 Distribution of the sample space（單位: mm）

3 SVM回歸原理

SVM 回歸算法的基本思想是將一個非線性的特征空間通過映射 Φ映射到更高維的線性特征空間，然后進行線性回歸。因此，對于數據集Y={(xi,yi)}，可以用下式進行回歸估計

那么回歸問題就變成如下的最優化問題

subject to

式中，C為懲罰系數；ξi為損失函數，即通常所稱的離群點。

式（2）是一個不等式優化問題，解起來是非常困難的。因此，通過Lagrange變換得到其對偶形式為

subject to

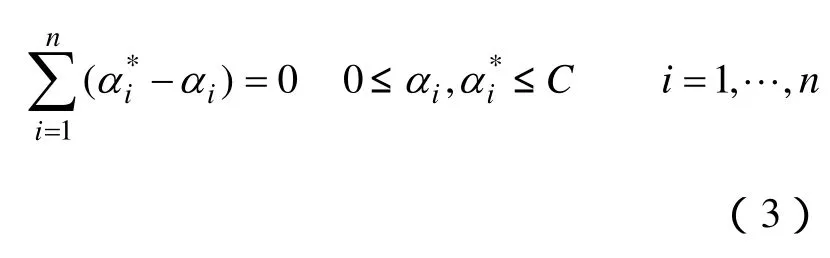
式中，α和α*為Lagrange乘子。

此時w的值為

由此，從式（2）的求解帶不等式約束的 w變成了求解α和α*。將式（4）代入式（1）中，回歸估計表達式變成

式中，(xi﹒x)是指高維空間的數據向量的內積，樣本空間中的數據是屬于低維空間的數據。

因此，將式（5）做如下變形

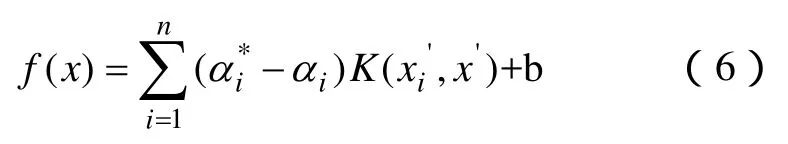
式中，K(xi′,x′)為核函數，其作用就是接受低維空間的數據向量得到高維空間的數據向量的內積。對于回歸問題，一般都采用徑向基（RBF）核函數。

4 SVM模型的參數尋優算法

在支持向量回歸估計算法中，RBF核函數的參數g以及懲罰系數C都是很重要的參數。其中，核函數參數g的選取決定了輸入空間到特征空間映射的方式，懲罰系數C用于平衡訓練誤差和模型復雜度。因此必須通過計算得到最優的參數C和g。對于 SVM 回歸模型的參數尋優，主要是通過最小化均方根誤差（MSE）來得到最優參數。

4.1 網格參數尋優算法

網格參數尋優算法的基本思想是按照設定好的步長，將C和g在各自空間劃分成若干網格，然后在每一個網格點上逐一計算以確定最優參數。在網格尋優算法計算過程中，通常采用V折交叉驗證法：將訓練數據分成n個大小相同的子集，首先用其中n-1個子集作為訓練集得到一個決策函數，用它預測測試集，得到該次循環在測試集上的分類準確率。這樣循環進行 n次，直到所有的子集都作為測試樣本被預測一遍，取n次預測所得準確率的平均值作為最終的準確率值，從而有效的避免了過擬合的問題。網格尋優算法的流程圖如圖4所示。圖5給出了參數尋優結果的等高線圖和三維圖。最優參數解為：C=3.031 4，g=0.062 5，最小MSE=0.021 876。

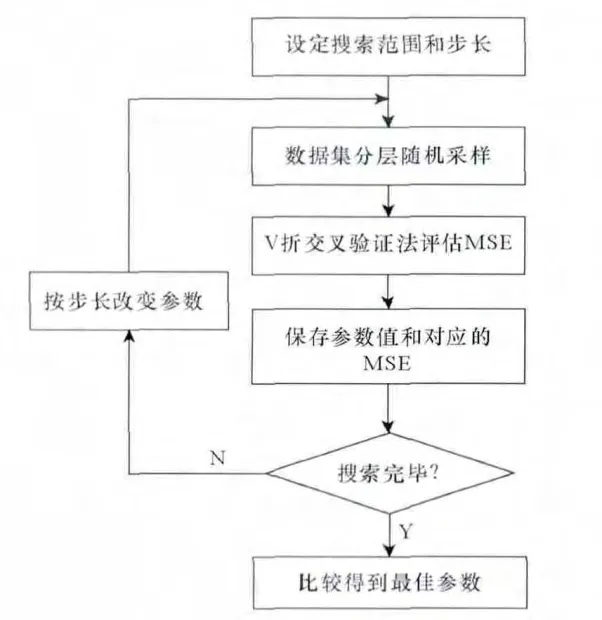
圖4 網格尋優算法流程圖Fig.4 The flow chart of grid parameter optimization algorithm

圖5 網格參數尋優算法結果Fig.5 The results of grid parameter optimization algorithm

4.2 GA參數尋優算法

遺傳算法（Genetic Algorithms，GA）根據適者生存、優勝劣汰等自然進化規則來進行搜索計算和問題求解。

標準GA算法雖然在理論上形成了一套完整的體系，但是由于存在早熟問題，經常使其得不到真正的最優解。因此對GA算法做如下改進：遺傳算法初期個體之間的差異性比較大，采用較大的交叉概率和較小的變異概率，有利于保存有用的遺傳信息；而在遺傳算法后期，個體之間適應度的差別很小，采用較小的交叉概率和較大的變異概率，能夠增加個體的多樣性，有利于進行全局搜索和克服早熟現象[10]。其算法流程圖如圖6所示。圖7給出了GA尋優算法的結果。最優參數解為：C=3.277 8，g=59.769 7，最小 MSE=0.032 364（種群數量pop=20）。

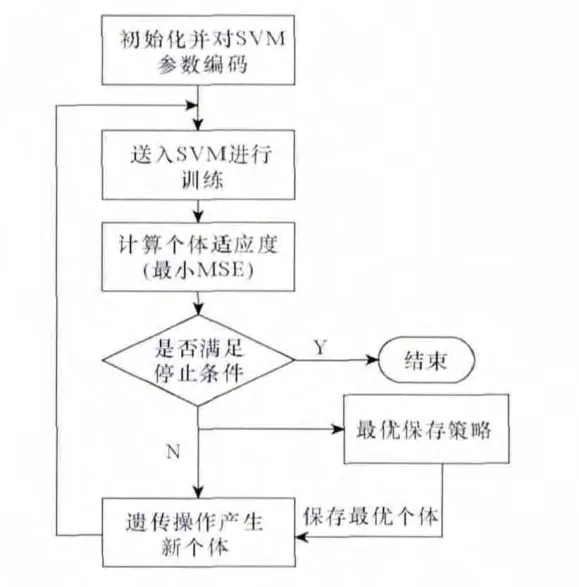
圖6 GA算法流程圖Fig.6 The flow chart of GA

圖7 GA參數尋優算法結果Fig.7 The result of GA

4.3 PSO參數尋優算法

粒子群優化算法模擬鳥群覓食過程中的遷徙和群集行為，是一種基于群體智能的進化計算技術[11]。

在PSO 算法中，群體的每個成員被稱為粒子，每個粒子在多維搜索空間中以一定的速度飛行，根據粒子本身的飛行經驗以及同伴的飛行經驗對自己的飛行速度進行動態調整，即每個粒子通過統計迭代過程中自身的最優值和群體的最優值來不斷地修正自己的前進方向和速度大小，從而形成群體尋優的正反饋機制。從而依據每個粒子對環境的適應度將個體逐步移到較優的區域，并最終搜索、尋找到問題的最優解。算法流程圖如圖8所示，圖9給出了PSO尋優算法的結果。最優參數解為：C=22.012 6，g=0.01，最小 MSE=0.021 697（參數 c1=1.5,c2=1.7,種群數量pop=20）。

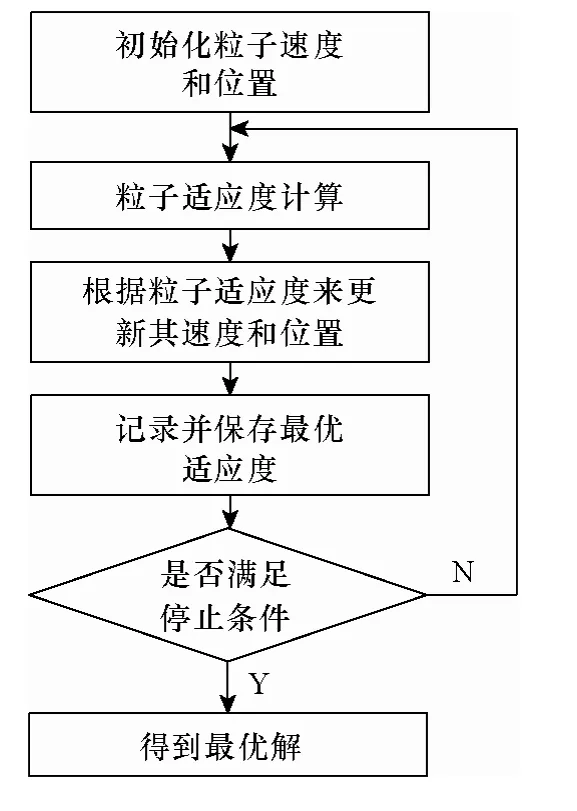
圖8 PSO算法流程圖Fig.8 The flow chart of PSO

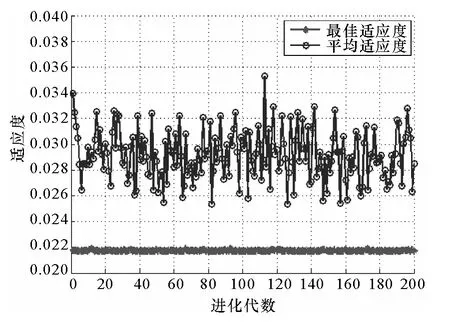
圖9 PSO參數尋優算法結果Fig.9 The result of PSO

4.4 三種算法結果的驗證

分別利用上述三種算法得到的C和g參數建立SVM模型，利用樣本空間的訓練集和測試集對三種模型進行驗證。圖10、圖11、圖12分別為網格尋優算法、GA尋優算法和PSO尋優算法的驗證結果。

由三種算法的結果圖看以看出，網格尋優算法和 PSO尋優算法雖然得到的C和 g的參數差別較大，但是計算得到的最小MSE值比較接近，并且通過測試集驗證得到了比較好的回歸結果。可以說明SVM模型的最優參數并不是唯一確定的。而GA尋優算法相比較其他兩種算法來說，計算得到的最小MSE值要大一些，而且從圖11的結果圖看出，GA尋優算法得到 SVM 模型在訓練集上能得到幾乎完美的回歸效果，然而在測試集上的回歸效果卻非常差，說明GA尋優算法得到的參數具有很差的推廣性，即泛化能力。

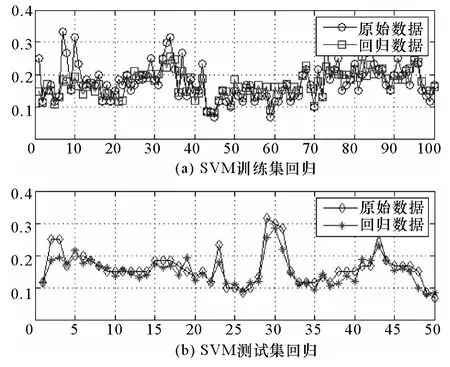
圖10 網格尋優算法驗證結果Fig.10 The validation results of grid parameter optimization algorithm

圖11 GA尋優算法結果Fig.11 The validation results of GA

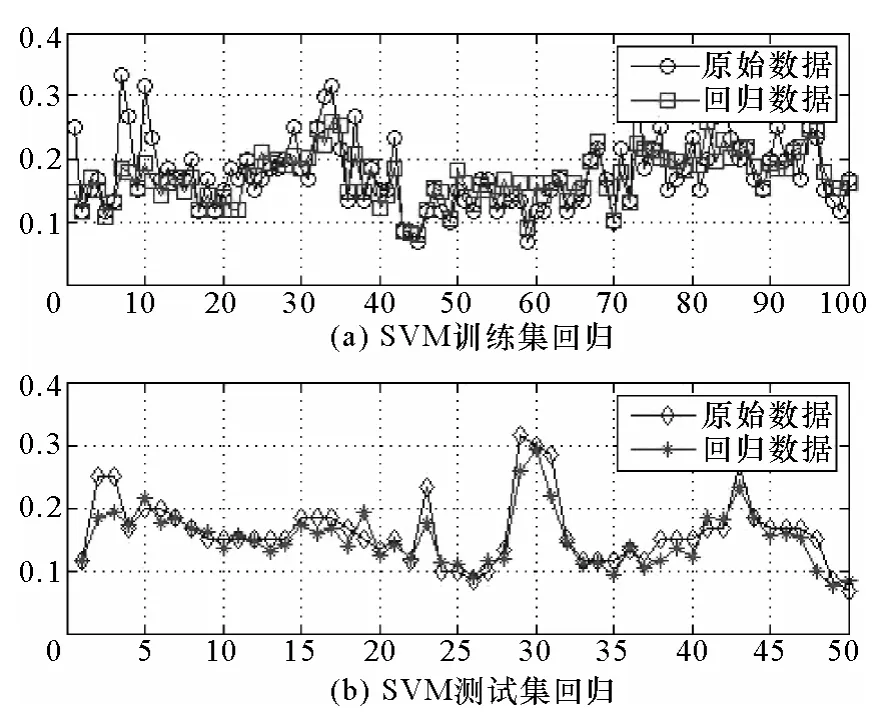
圖12 PSO尋優算法結果Fig.12 The validation results of PSO

5 結論

對于永磁球形電機的 SVM 回歸模型的參數尋優，GA參數尋優算法計算得到的參數其SVM模型的回歸效果具有很差的泛化能力，說明GA尋優算法并不適用于球形電機SVM回歸模型的參數尋優。而網格參數尋優算法和 PSO參數尋優算法雖然計算得到的參數 C和 g并不相同，但是各自的 SVM模型的回歸效果基本相同。這也說明了 SVM 模型最優參數并不是唯一確定的。另外，本文所用的樣本空間比較小，所以兩種算法的計算時間差別不大。如果是大樣本空間的話，網格參數尋優算法比PSO尋優算法的時間代價要大的多。

[1] Vladimir Vapnik,Esther Levin,Yann Le Cun.Measuring the VC-dimension of learning machines[J],Neural Computation,1994,6(5): 851-867.

[2] Nello Cristianini,John Shawe Taylor.支持向量機導論[M].李國正等譯.北京: 北京電子工業出版社,2004.

[3] Olivier Chapelle,Vladimir Vapnik,Olivier Bousquet,et al.Choosing multiple parameters for support vector machines[J].Machine Learning,2002,46(1): 131-159.

[4] 李兵,姚全珠,羅作民,等.基于網格模式搜索的支持向量機模型選擇[J].計算機工程與應用,2008,44(15): 136-138.Li Bing,Yao Quanzhu,Lou Zuomin,et al.Gird-pattern method for model selection of support vector machines[J].Computer Engineering and Applications,2008,44(15): 136-138.

[5] Chen P W,Jungying W,Hahnming L.Model selection of SVMs using GA approach[C].Proceedings of IEEE International Joint Conference on Neural Networks,Piscataway,2004: 2035-2040.

[6] Wang Cunrui,Duan Xiaodong,Liu Xiangdong,et al.A modified basic particle swarm optimization algorithm[J].Computer Engineering,2004,30(21):35-37.

[7] 任洪娥,霍滿冬.基于PSO 優化的SVM 預測應用研究[J].計算機應用研究,2009,26(3): 867-869.Ren Honge,Huo Dongman.Support vector machine optimized by particle swarm optimization algorithm for holding nail force forecasting[J].Application Research of Computers,2009,26(3): 867-869.

[8] 李爭.仿人機器人關節用永磁球形步進電動機的基礎研究[D].合肥: 合肥工業大學,2006.

[9] 茆詩松,王金玉,周紀薌.參數設計思想與方法的研究[J].應用概率統計,1993,9(4): 438- 448.Mao Shisong,Wang Jinyu,Zhou Jixiang,et al.Research of idea and mebod of parameter design[J].Chinese Journal of Applied Probability and Statistics,1993,9(4): 438-448.

[10] 劉東平,單甘霖,張岐龍.基于改進遺傳算法的支持向量機參數優化[J].微計算機應用,2010,31(5):11-15.Liu Dongping,Shan Ganlin,Zhang Qilong.Parameters optimization of support vector machine based on improved genetic algorithm[J].Microcomputer Applications,2010,31(5): 11-15.

[11] Kennedy J,Eberhart R.Particle swarm optimization[C].Proc.IEEE International Conf.on Neural Networks,1995: 1942-1948.